Đề thi giữa kì 1 Toán 6 - Đề số 1

Đề bài

Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Cho M  là tập hợp các tháng (dương lịch) trong năm có \(31\) ngày. Phần tử không thuộc tập hợp \(M\) là

     A.  Tháng \(5\)                  B. Tháng \(6\)                   C. Tháng \(7\)                   D. Tháng \(8\).

Câu 2: Tập hợp các chữ cái trong từ “\(TOÁN\)\(6\)” là

     A. {\(T;\)\(O;\)\(A;\)\(N;\)\(6\)}                               B. {\(T;\)\(O;\)\(A;\)\(N\)}                  C. {\(T;\)\(A;\)\(N\)}          D. {\(T;\)\(O;\)\(A;\)\(N;\)\(S;\)\(U\)}.

Câu 3: Giá trị của x trong phép tính \({2^{x + 1}}{.2^2} = {\rm{ }}16\) là

     A. \(4\)                              B. \(3\)                               C. \(2\)                              D. \(1\).

Câu 4: Tập hợp tất cả các ước của 6 là

     A. {2; 3}                            B. {0; 1; 2; 3; 6}                C. {1; 2; 6}                        D. {1; 2; 3; 6}.

Câu 5: Nếu \(a\)⁝ 3; \(b\)⁝ 3; \(c\)⁝ 3 thì kết luận nào sau đây là đúng?           

     A. \(\left( {a + b + c} \right) \vdots 3\)                        B. \(\left( {a + b + c} \right) \vdots 6\)               C. \(\left( {a + b + c} \right) \vdots 9\)                                                   D. \(\left( {a + b + c} \right) \vdots 27\).

Câu 6: Viết số \(27\) dưới dạng số La Mã ta được

     A. \(XIXI\)                          B. \(XVVII\)                        C. \(XXII\);                         D. \(XXVII\).

Câu 7:Cho số M = \(\overline {1a7b} \). Giá trị của \(a\) và \(b\) để M  chia hết cho \(2;5;9\) là

     A. \(a = 4,{\rm{ }}b = 5\)      B.\(a = 1,b = 0\)                  C. \(a = 5,b = 5\)                 D. \(a = 0,b = 1\).

Câu 8: Cho tam giác đều \(MNP\) có \(MN\) = \(7cm\). Độ dài \(NP\) và \(MP\) là

     A. \(NP\; = {\rm{ }}6cm;MP = \;7cm\)                             B. \(NP = {\rm{ }}6cm;\;\;MP = {\rm{ }}6cm\)

     C. \(NP = 7cm;\;MP = {\rm{ }}7cm\)                               D. \(NP = {\rm{ }}7cm;\;MP = {\rm{ }}6cm\).

Câu 9: Khẳng định sai trong những khẳng định dưới đây là:

     A. Trong hình thoi, hai đường chéo vuông góc

     B. Trong hình thoi, \(4\)cạnh bằng nhau

     C. Trong hình thoi, \(2\)đường chéo bằng nhau

     D. Trong hình thoi, các cạnh đối song song và bằng nhau.

Câu 10: Chọn câu sai. Cho \(ABCD\) là hình bình hành. Khi đó:                     

     A. \(AB\) = \(CD\)              B. \(AD\) =\(BC\)               C.\(\angle A = \angle C\)                 D. \(AC\) = \(BD\).

Câu 11: Một mảnh giấy hình chữ nhật có diện tích \(96c{m^2}\), độ dài một cạnh là \(12cm\). Chu vi của mảnh giấy là:

     A. \(20cm\)                        B. \(40cm\)                    C. \(60cm\)                   D. \(80cm\).

Câu 12:Khi cắt 6 hình tam giác đều có cạnh bằng 6cm và ghép thành 1 lục giác đều (Hình vẽ). Độ dài đường chéo chính của lục giác đều là:

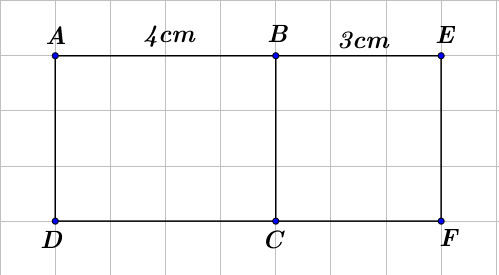
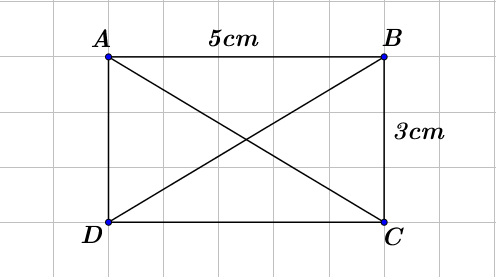
Phần II. Tự luận (7 điểm):

Bài 1: (1 điểm) Viết tập hợp sau bằng 2 cách và tính số phần tử của tập hợp đó.

a) Tập hợp B gồm các số tự nhiên lớn hơn 9 và nhỏ hơn 12

b) Tập hợp C gồm các số tự nhiên chẵn nhỏ hơn 10.

Bài 2: (1 điểm) Thực hiện các phép tính sau (Tính nhanh nếu có thể):

a) \(237 + 86 + 63 + 214\)                                                    b) \(45 + [32 - (4 + 3.5)]\)

c) \(5.25.2.16.4\)                                                                d) \({10^4}:[4.({5^2} - 5){\rm{] + }}25\).

Bài 3: (1 điểm) Tìm số tự nhiên x thỏa mãn.

a) \(\left( {x - 45} \right).27 = 0\)                                                                                    b) \(3x - {2^4} = {5^3}.\)

Bài 4: (1 điểm) Không tính, hãy xét xem tổng (hiệu) sau đây có chia hết cho 2 không? Có chia hết cho 5 không? Vì sao?

a) \(125 + 360\)                        b) \(2.3.4.5.6 + 82\)             c) \(2.3.4.5.6 - 95\).

Bài 5: (1 điểm) Lan có \(50000\) đồng để mua vở và bút bi. Lan mua \(8\) quyển vở và \(5\)bút bi. Số tiền Lan còn thừa là \(8000\) đồng. Hỏi giá tiền mỗi quyển vở là bao nhiêu? Biết rằng giá mỗi chiếc bút bi là \(2000\) đồng.

Bài 6: (1 điểm)

a) Vẽ hình chữ nhật \(ABCD\) biết cạnh  \(AB = 5cm\) và cạnh \(BC = 3cm\)

b) Hãy chỉ ra các cặp cạnh bằng nhau trong hình vẽ

c) Tính chu vi, diện tích của hình chữ nhật \(ABCD\) vừa vẽ;

Bài 7: (1 điểm) Cho biết \(ABCD\) là hình chữ nhật và \(BEFC\) là hình vuông. Biết \(AB\) = 4cm và \(BE\) = 3cm. Tính diện tích hình chữ nhật \(ABCD\)

Lời giải

Phần I: Trắc nghiệm

Câu 1

Phương pháp:

Dùng quy ước bàn tay để tính số ngày của 12 tháng trong năm.

Cách giải:

Tháng 6 là tháng có 30 ngày.

Tháng 5,7,8 là tháng có 31 ngày.

Chọn B.

Câu 2

Phương pháp:

Sử dụng phương pháp liệt kê các phần tử của tập hợp: Liệt kê các phần tử trong dấu ngoặc { }, mỗi phần tử được liệt kê duy nhất 1 lần, theo thứ tự tùy ý, ngăn cách nhau bởi dấu ;

Cách giải:

Tập hợp các chữ cái là \(\left\{ {T;O;A;N} \right\}\). Số 6 không phải là chữ cái nên không được liệt kê.

Chọn B.

Câu 3

Phương pháp:

Sử dụng phép tính nhân hai lũy thừa cùng cơ số để tìm \(x.\)

\({a^m}.{a^n} = {a^{m + n}}\)

Nếu \({a^k} = {a^p}(a \ne 1) \Rightarrow k = p\)

Cách giải:

Ta có: \({2^{x + 1}}\;.{\rm{ }}{2^2} = {\rm{ }}16\)

\({2^{x + 3}} = {2^4} \Rightarrow x + 3 = 4 \Rightarrow x = 1\)

Chọn D.

Câu 4

Phương pháp:

Viết các số tự nhiên là ước của 6.

Cách giải:

Tập hợp các ước của 6 là: \(\left\{ {1;2;3;6} \right\}\)

Chọn D.

Câu 5

Phương pháp:

Sử dụng quan hệ chia hết của một tổng: Nếu a, b chia hết cho m thì (a+b) cũng chia hết cho m.

Cách giải:

Ta có: \(a,b,c\) đều chia hết cho 3 nên tổng \(a + b + c\) chia hết cho 3.

Chọn A.

Câu 6

Phương pháp

Sử dụng bảng số La Mã.

Cách giải:

Số 27 viết dưới dạng số La Mã là \(XXVII\)

Chọn D.

Câu 7

Phương pháp:

Sử dụng dấu hiệu chia hết cho 2,5,9

Cách giải:

M = \(\overline {1a7b} \)

Ta có: M  chia hết cho \(2;5\) nên \(b \in \left\{ {0;5} \right\}\). Mà M chia hết cho 2 nên \(b = 0\).

Khi đó ta có \(M = \overline {1a70} \)

Do M chia hết cho 9 nên \(1 + a + 7 + 0\) chia hết cho 9 \( \Rightarrow a + 8\) chia hết cho 9

Suy ra \(a = 1\)

Chọn B.

Câu 8

Phương pháp

Sử dụng định nghĩa của tam giác đều.

Cách giải

Tam giác đều là tam giác có 3 cạnh bằng nhau nên \(NP = 7cm;\;MP = {\rm{ }}7cm\)

Chọn C.

Câu 9

Phương pháp

Sử dụng tính chất của hình thoi: bốn cạnh bằng nhau, hai cặp cạnh đối song song với nhau, hai đường chép vuông góc với nhau.

Cách giải

Khẳng định sai là: Trong hình thoi, \(2\)đường chéo bằng nhau.

Chọn C.

Câu 10

Phương pháp

Sử dụng tính chất của hình bình hành: hai cặp cạnh đối song song và bằng nhau, hai cặp góc đối bằng nhau

Cách giải

Khẳng định sai là \(AC = BD\) vì trong hình bình hành, hai đường chéo không bằng nhau.

Chọn D.

Câu 11

Phương pháp

Sử dụng công thức tính diện tích của hình chữ nhật để tính được độ dài của cạnh còn lại.

Dùng công thức tính chu vi hình chữ nhật.

Cách giải

Do diện tích của hình chữ nhật là \(96c{m^2}\) và độ dài một cạnh là \(12cm\) nên độ dài cạnh còn lại là: \(96:12 = 8\left( {cm} \right)\)

Chu vi của hình chữ nhật là: \(\left( {12 + 8} \right).2 = 40\,\left( {cm} \right)\)

Chọn B.

Câu 12

Phương pháp

Quan sát hình vẽ để rút ra mối liên hệ giữa đường chéo chính và cạnh của tam giác.

Cách giải

Đường chéo chính được tạo bởi 2 cạnh của tam giác đều cạnh 6cm nên có độ dài là: \(6 + 6 = 12\)(cm)

Chọn A.

Phần II: Tự luận

Bài 1

Phương pháp

Sử dụng phương pháp liệt kê các phần tử của tập hợp: Liệt kê các phần tử trong dấu ngoặc { }, mỗi phần tử được liệt kê duy nhất 1 lần, theo thứ tự tùy ý, ngăn cách nhau bởi dấu ;

Cách giải

a) Tập hợp B gồm các số tự nhiên lớn hơn 9 và nhỏ hơn 12 là:

C1: \(B = \left\{ {10;11} \right\}\)

C2: \(B = \left\{ x \in N|9 < x < 12 \right\} \)

Số phần tử của tập hợp B là 2.

b) Tập hợp C gồm các số tự nhiên chẵn nhỏ hơn 10 là:

C1: \(C = \left\{ {0;2;4;6;8} \right\}\)

C2: \(C = \left\{x \in N| x \vdots 2; x <10\right\}\)

Số phần tử của tập hợp C là 5.

Bài 2

Phương pháp

Sử dụng các quy tắc về thứ tự thực hiện phép tính:

Thực hiện tính trong ngoặc trước, nếu biểu thức chứa nhiều dấu ngoặc thì tính theo thứ tự ( ) => [ ] => { }

Thực hiện phép tính theo thứ tự lũy thừa => nhân, chia => cộng, trừ

Cách giải

Bài 3

Phương pháp

Chuyển vế để tìm được \(x\).

Sử dụng phép tính giá trị lũy thừa của một số.

Cách giải

Bài 4

Phương pháp

Sử dụng kiến thức về dấu hiệu chia hết cho 2, cho 5 và tính chất chia hết của một tổng, hiệu, tích

Cách giải

+) Nhận xét câu a) ta có:

\(125\) và \(360\) đều chia hết cho 5 nên \(125 + 360\) chia hết cho 5.

\(125\) không chia hết cho \(2\) nên \(125 + 360\) không chia hết cho \(2\).

+) Nhận xét câu b) ta có:

\(2.3.4.5.6\) và \(82\) đều chia hết cho \(2\) nên \(2.3.4.5.6 + 82\) chia hết cho \(2\).

\(82\) không chia hết cho \(5\) nên \(2.3.4.5.6 + 82\) không chia hết cho \(5.\)

+) Nhận xét câu c) ta có:

\(2.3.4.5.6\) và \(95\) đều chia hết cho \(5\) nên \(2.3.4.5.6 - 95\) chia hết cho \(5\).

\(95\) không chia hết cho \(2\) nên \(2.3.4.5.6 - 95\) không chia hết cho \(2\).

Bài 5

Phương pháp

Tính số tiền Lan mua cả vở và bút bi. Sau đó trừ đi số tiền Lan đã mua bút bi, ta tìm được số tiền Lan mua vở.

Lấy tổng số tiền mua vở chia cho số quyển vở, ta tìm được giá của một quyển.

Cách giải

Số tiền Lan mua vở và bút bi là:

\(50000 - 8000 = 42000\) (đồng)

Số tiền Lan mua bút bi là:

\(2000.5 = 10000\) (đồng)

Số tiền Lan mua vở là:

\(42000 - 10000 = 32000\) (đồng)

Gía tiền mỗi quyển vở Lan mua là:

\(32000:8 = 4000\) (đồng)

Bài 6

Phương pháp

Sử dụng cách vẽ hình chữ nhật.

Dựa vào các tính chất của hình chữ nhật để tìm ra được các cặp cạnh bằng nhau.

Sử dụng công thức tính chu vi và diện tích của hình chữ nhật.

Cách giải

Các cặp cạnh bằng nhau: \(AB = CD;\,AD = BC;\,AC = BD\)

Chu vi hình chữ nhật \(ABCD\) là: \(\left( {5 + 3} \right).2 = 16\left( {cm} \right)\)

Diện tích hình chữ nhật \(ABCD\) là: \(5.3 = 15\left( {c{m^2}} \right)\)

Bài 7

Phương pháp

Tính được chiều rộng của hình chữ nhật thông qua việc tính cạnh của hình vuông.

Sử dụng công thức tính diện tích hình chữ nhật.

Cách giải

Do \(BEFC\) là hình vuông nên \(BE = BC = 3cm\)

Diện tích hình chữ nhật \(ABCD\) là: \(4.3 = 12\left( {c{m^2}} \right)\)