Bài 121 : Luyện tập chungGiải bài tập 1, 2, 3, 4 trang 42 VBT toán 4 bài 121 : Luyện tập chung với lời giải chi tiết và cách giải nhanh, ngắn nhất Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
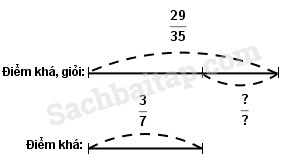
Bài 1 Tìm \(y\) : a) \(\displaystyle y + {3 \over 4} = {4 \over 5}\) b) \(\displaystyle y - {3 \over {11}} = {9 \over {22}}\) c) \(\displaystyle {9 \over 2} - y = {2 \over 9}\) Phương pháp giải: Áp dụng các quy tắc : - Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết. - Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ. - Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu. Lời giải chi tiết: \( \displaystyle a)\,\,y + {3 \over 4} = {4 \over 5} \) \( \displaystyle y = \,\,{4 \over 5} - {3 \over 4} \) \( \displaystyle y = \,\,{1 \over {20}} \) \( \displaystyle b)\,\,y - {3 \over {11}} = {9 \over {22}} \) \( \displaystyle y = {{15} \over {22}} \) \( \displaystyle c)\,\,{9 \over 2} - y = {2 \over 9} \) \( \displaystyle y = {{77} \over {18}} \) Bài 2 Tính và so sánh giá trị của hai biểu thức sau : \( \displaystyle \left( {{9 \over 2} - {5 \over 2}} \right) - {3 \over 4}\) \(\displaystyle {9 \over 2} - \left( {{5 \over 2} + {3 \over 4}} \right)\) Vậy \( \displaystyle \left( {{9 \over 2} - {5 \over 2}} \right) - {3 \over 4}\,...\,{9 \over 2} - \left( {{5 \over 2} + {3 \over 4}} \right)\) Phương pháp giải: Áp dụng quy tắc : Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau. Lời giải chi tiết: \( \displaystyle \left( {{9 \over 2} - {5 \over 2}} \right) - {3 \over 4} = {4 \over 2} - {3 \over 4} ={8 \over 4} - {{3} \over 4} \)\( \displaystyle= {5 \over 4} \) Vậy \( \displaystyle \left( {{9 \over 2} - {5 \over 2}} \right) - {3 \over 4} = {9 \over 2} - \left( {{5 \over 2} + {3 \over 4}} \right).\) Bài 3 Tính bằng cách thuận tiện nhất: \(a)\; \displaystyle{{18} \over {15}} + {7 \over {15}} + {{12} \over {15}}\) \(b)\;\displaystyle {9 \over 7} + {8 \over 7} + {{11} \over 7}\) Phương pháp giải: Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm các phân số thích hợp lại với nhau. Lời giải chi tiết: a) \( \displaystyle {{18} \over {15}} + {7 \over {15}} + {{12} \over {15}} \) \( \displaystyle = \left( {{{18} \over {15}} + {{12} \over {15}}} \right) + {7 \over {15}} \) b) \( \displaystyle {9 \over 7} + {8 \over 7} + {{11} \over 7} \) \( \displaystyle = \left( {{9 \over 7} + {{11} \over 7}} \right) + {8 \over 7} \) Bài 4 Trong các bài kiểm tra môn Toán cuối học kì I của khối lớp Bốn có \( \displaystyle{3 \over 7}\) có bài đạt điểm khá. Biết số bài đạt điểm giỏi và điểm khá là \( \displaystyle{{29} \over {35}}\) số bài kiểm tra. Hỏi số bài đạt điểm giỏi chiếm bao nhiêu phần của bài kiểm tra? Phương pháp giải: Muốn tìm phân số chỉ số bài đạt điểm giỏi ta lấy phân số chỉ số bài đạt điểm giỏi và điểm khá trừ đi phân số chỉ số bài đạt điểm khá. Lời giải chi tiết: Tóm tắt
Bài giải Số bài đạt điểm loại giỏi là: \( \displaystyle {{29} \over {35}} - {3 \over 7} = {{14} \over {35}}\) (số bài kiểm tra) Đáp số: \( \displaystyle {{14} \over {35}}\) số bài kiểm tra. Loigiaihay.com
|



















Danh sách bình luận