Trắc nghiệm Tổng hợp câu hay và khó chương 2 Toán 9Đề bài Cho đường thẳng \(\left( {{d_1}} \right):y = x + 2\) và đường thẳng \(\left( {{d_2}} \right):y = \left( {2{m^2} - m} \right)x + {m^2} + m\). Câu 1
Tìm \(m\) để \(({d_1})//({d_2})\).
Câu 2
Gọi \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\). Viết phương trình đường thẳng \(({d_3})\) đi qua \(A\) vuông góc với \(({d_1})\).
Câu 3
Khi \(({d_1})//({d_2})\). Hãy tính khoảng cách giữa hai đường thẳng \(({d_1}),\left( {{d_2}} \right)\).
Câu 4
Tính diện tích tam giác \(OMN\) với \(M,N\) lần lượt là giao điểm của \(({d_1})\) với các trục tọa độ \(Ox,Oy\).
Cho đường thẳng \(mx + \left( {2 - 3m} \right)y + m - 1 = 0\) \((d)\). Câu 5
Tìm điểm cố định \(I\) mà đường thẳng \((d)\) luôn đi qua.
Câu 6
Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \((d)\) là lớn nhất.
Xác định các hệ số \(a,b\) của hàm số \(y = ax + b\) để: Câu 7
Đồ thị của nó đi qua hai điểm \(A\left( {1;3} \right),B\left( {2;4} \right)\)
Câu 8
Đồ thị của nó cắt trục tung tại điểm có tung độ bằng \( - 4\) và cắt trục hoành tại điểm có hoành độ bằng \(2\).
Câu 9 :
Cho $2$ đường thẳng $d:y = x + 3;d':y = \dfrac{{ - 2}}{3}x + \dfrac{4}{3}$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $C$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành; $B$ và $D$ lần lượt là giao điểm của $d$ và $d'$ với trục tung. Khi đó diện tích tam giác $CMB$ là:
Câu 10 :
Tìm $m$ để đường thẳng $d:y = mx + 1$ cắt đường thẳng $d':y = 2x - 1$ tại $1$ điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$.
Câu 11 :
Có bao nhiêu giá trị nguyên của $m$ để $2$ đường thẳng $d:y = mx - 2;d':y = 2x + 1$ cắt nhau tại điểm có hoành độ là số nguyên.
Câu 12 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Câu 13 :
Cho đường thẳng $d:y = ({m^2} - 2m + 2)x + 4$. Tìm $m$ để $d$ cắt $Ox$ tại $A$ và cắt $Oy$ tại $B$ sao cho diện tích tam giác $AOB$ lớn nhất.
Câu 14 :
Cho tam giác $ABC$ có đường thẳng $BC:y = - \dfrac{1}{3}x + 1$ và $A\left( {1,2} \right)$ . Viết phương trình đường cao $AH$ của tam giác $ABC$ .
Câu 15 :
Điểm cố định mà đường thẳng $d:y = \dfrac{{\sqrt k + 1}}{{\sqrt 3 - 1}}x + \sqrt k + 3 \, (k \ge 0)$ luôn đi qua là:
Câu 16 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Câu 17 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( {1;1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Viết phương trình đường trung trực của đoạn thẳng $AB$.
Cho hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 5\\mx - y = 4\end{array} \right.\)\(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\) Câu 18
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) trong đó \(x,y\) trái dấu.
Câu 19
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn \(x = \left| y \right|\).
Cho đường thẳng \(\left( {{d_1}} \right):y = x + 2\) và đường thẳng \(\left( {{d_2}} \right):y = \left( {2{m^2} - m} \right)x + {m^2} + m\). Câu 20
Tìm \(m\) để \(({d_1})//({d_2})\).
Câu 21
Gọi \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\). Viết phương trình đường thẳng \(({d_3})\) đi qua \(A\) vuông góc với \(({d_1})\).
Câu 22
Khi \(({d_1})//({d_2})\). Hãy tính khoảng cách giữa hai đường thẳng \(({d_1}),\left( {{d_2}} \right)\).
Câu 23
Tính diện tích tam giác \(OMN\) với \(M,N\) lần lượt là giao điểm của \(({d_1})\) với các trục tọa độ \(Ox,Oy\).
Câu 24 :
Cho $2$ đường thẳng: $d:y = x + 3;d':y = \dfrac{{ - 2}}{3}x + \dfrac{4}{3}$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $C$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành; $B$ và $D$ lần lượt là giao điểm của $d$ và $d'$ với trục tung. Khi đó diện tích tam giác $CMB$ là:
Cho đường thẳng: \(mx + \left( {2 - 3m} \right)y + m - 1 = 0\) \((d)\). Câu 25
Tìm điểm cố định \(I\) mà đường thẳng \((d)\) luôn đi qua.
Câu 26
Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \((d)\) là lớn nhất.
Xác định các hệ số \(a,b\) của hàm số \(y = ax + b\) để: Câu 27
Đồ thị của nó đi qua hai điểm \(A\left( {1;3} \right),B\left( {2;4} \right)\):
Câu 28
Đồ thị của nó cắt trục tung tại điểm có tung độ bằng \( - 4\) và cắt trục hoành tại điểm có hoành độ bằng \(2\).
Cho hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 5\\mx - y = 4\end{array} \right.\)\(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\) Câu 29
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) trong đó $x,y$ trái dấu.
Câu 30
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn $x = \left| y \right|$.
Cho hệ phương trình: \(\left\{ \begin{array}{l}x + my = m + 1\\mx + y = 3m - 1\end{array} \right.\) \(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\)
Câu 31
Tìm số nguyên \(m\) sao cho hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) mà $x,y$ đều là số nguyên.
Câu 32
Trong trường hợp hệ có nghiệm duy nhất \(\left( {x;y} \right)\) thì điểm \(M\left( {x;y} \right)\) luôn chạy trên đường thẳng nào dưới đây?
Câu 33
Tìm \(m\) để hệ trên có nghiệm duy nhất sao cho \(x.y\) đạt giá trị nhỏ nhất.
Câu 34 :
Tìm $m$ để đường thẳng $d:y = mx + 1$ cắt đường thẳng $d':y = 2x - 1$ tại $1$ điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$.
Câu 35 :
Giá trị nguyên có thể có của $m$ để $2$ đường thẳng $d:y = mx - 2;d':y = 2x + 1$ cắt nhau tại điểm có hoành độ là số nguyên.
Câu 36 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Lời giải và đáp án Cho đường thẳng \(\left( {{d_1}} \right):y = x + 2\) và đường thẳng \(\left( {{d_2}} \right):y = \left( {2{m^2} - m} \right)x + {m^2} + m\). Câu 1
Tìm \(m\) để \(({d_1})//({d_2})\).
Đáp án : C Phương pháp giải :
Hai đường thẳng \(\left( d \right):y = ax + b;\,\left( {d'} \right):y = a'x + b'\) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Lời giải chi tiết :
Đường thẳng \(({d_1})//({d_2})\) khi và chỉ khi \(\left\{ \begin{array}{l}2{m^2} - m = 1\\{m^2} + m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 1} \right)\left( {2m + 1} \right) = 0\\\left( {m - 1} \right)\left( {m + 2} \right) \ne 0\end{array} \right. \Leftrightarrow m = - \dfrac{1}{2}\). Vậy với \(m = - \dfrac{1}{2}\) thì \(({d_1})//({d_2})\). Câu 2
Gọi \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\). Viết phương trình đường thẳng \(({d_3})\) đi qua \(A\) vuông góc với \(({d_1})\).
Đáp án : A Phương pháp giải :
+ Tìm điểm A. + Sử dụng Hai đường thẳng \(\left( d \right):y = ax + b;\,\left( {d'} \right):y = a'x + b'\) vuông góc với nhau khi \(a.a' = - 1\) Lời giải chi tiết :
Vì \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\) suy ra tung độ điểm \(A\) là \(y = 2 + 2 = 4 \Rightarrow A\left( {2;4} \right)\) . Đường thẳng \(\left( {{d_1}} \right)\) có hệ số góc là \(a = 1\), đường thẳng \(\left( {{d_2}} \right)\) có hệ số góc là \(a' \Rightarrow a'.1 = - 1 \Rightarrow a' = - 1\) . Đường thẳng \(\left( {{d_3}} \right)\) có dạng \(y = - x + b\). Vì \(\left( {{d_3}} \right)\) đi qua \(A\left( {2;4} \right)\) suy ra \(4 = - 2 + b \Rightarrow b = 6\). Vậy đường thẳng \(\left( {{d_3}} \right)\) là \(y = - x + 6\). Câu 3
Khi \(({d_1})//({d_2})\). Hãy tính khoảng cách giữa hai đường thẳng \(({d_1}),\left( {{d_2}} \right)\).
Đáp án : D Phương pháp giải :
Khi \(({d_1})//({d_2})\) thì khoảng cách giữa hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cũng chính là khoảng cách giữa hai điểm \(A,B\) lần lượt thuộc \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) sao cho \(AB \bot ({d_1}),AB \bot \left( {{d_2}} \right)\). Sử dụng \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \) Lời giải chi tiết :
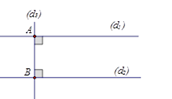 Đường thẳng \(({d_1})//({d_2})\) khi và chỉ khi \(\left\{ \begin{array}{l}2{m^2} - m = 1\\{m^2} + m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 1} \right)\left( {2m + 1} \right) = 0\\\left( {m - 1} \right)\left( {m + 2} \right) \ne 0\end{array} \right. \Leftrightarrow m = - \dfrac{1}{2}\). Vậy với \(m = - \dfrac{1}{2}\) thì \(({d_1})//({d_2})\). Khi đó \(\left( {{d_2}} \right):y = x -\dfrac{1}{4}\) Lại có theo câu trước đường thẳng \(\left( {{d_3}} \right)\) là \(y = - x + 6\). Khi \(({d_1})//({d_2})\) thì khoảng cách giữa hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cũng chính là khoảng cách giữa hai điểm \(A,B\) lần lượt thuộc \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) sao cho \(AB \bot ({d_1}),AB \bot \left( {{d_2}} \right)\). Hình vẽ: Gọi \(B\) là giao điểm của đường thẳng \(({d_3})\) và \(({d_2})\). Phương trình hoành độ giao điểm của \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right)\) là: \( - x + 6 = x - \dfrac{1}{4} \Leftrightarrow x = \dfrac{{25}}{8} \Rightarrow y = \dfrac{{23}}{8} \Rightarrow B\left( {\dfrac{{25}}{8};\dfrac{{23}}{8}} \right)\). Vậy độ dài đoạn thẳng \(AB\) là: \(AB = \sqrt {{{\left( {\dfrac{{25}}{8} - 2} \right)}^2} + {{\left( {\dfrac{{23}}{8} - 4} \right)}^2}} = \dfrac{{9\sqrt 2 }}{8}\). Câu 4
Tính diện tích tam giác \(OMN\) với \(M,N\) lần lượt là giao điểm của \(({d_1})\) với các trục tọa độ \(Ox,Oy\).
Đáp án : C Phương pháp giải :
+ Tìm tọa độ M, N. Tính độ dài \(OM;ON\) sau đó tính diện tích tam giác \(OMN.\) Lời giải chi tiết :
Gọi \(M,N\) lần lượt là giao điểm của đường thẳng \(\left( {{d_1}} \right)\) với các trục tọa độ \(Ox,Oy\). Ta có: Cho \(y = 0 \Rightarrow x = - 2 \Rightarrow M\left( { - 2;0} \right)\), cho \(x = 0 \Rightarrow y = 2 \Rightarrow N\left( { 0;2} \right)\). Từ đó suy ra \(OM = ON = 2\). Tam giác $OMN$ vuông cân tại \(O\) nên \({S_{OMN}} = \dfrac{1}{2}OM.ON = 2\) (đvdt). Cho đường thẳng \(mx + \left( {2 - 3m} \right)y + m - 1 = 0\) \((d)\). Câu 5
Tìm điểm cố định \(I\) mà đường thẳng \((d)\) luôn đi qua.
Đáp án : A Phương pháp giải :
Đưa về phương trình bậc nhất ẩn \(m\) là \(am + b = 0\) đúng với mọi \(m \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\) Lời giải chi tiết :
Gọi \(I\left( {{x_0};{y_0}} \right)\) là điểm cố định mà đường thẳng \((d)\) luôn đi qua với mọi \(m\) khi đó ta có: \(m{x_0} + \left( {2 - 3m} \right){y_0} + m - 1 = 0\,\forall m\)\( \Leftrightarrow m\left( {{x_0} - 3{y_0} + 1} \right) + 2{y_0} - 1 = 0\,\forall m\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_0} - 3{y_0} + 1 = 0\\2{y_0} - 1 = 0\end{array} \right.\). Hay\(\left\{ \begin{array}{l}{x_0} = \dfrac{1}{2}\\{y_0} = \dfrac{1}{2}\end{array} \right. \Leftrightarrow I\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)\). Câu 6
Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \((d)\) là lớn nhất.
Đáp án : B Phương pháp giải :
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên đường thẳng \((d)\). Ta có: \(OH \le OI\) suy ra \(OH\) lớn nhất bằng \(OI\) khi và chỉ khi \(H \equiv I \Leftrightarrow OI \bot (d)\).
Lời giải chi tiết :
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên đường thẳng \((d)\). Ta có: \(OH \le OI\) suy ra \(OH\) lớn nhất bằng \(OI\) khi và chỉ khi \(H \equiv I \Leftrightarrow OI \bot (d)\). Đường thẳng qua \(O\) có phương trình: \(y = ax\) do \(I\left( {\dfrac{1}{2};\dfrac{1}{2}} \right) \in OI \Rightarrow \dfrac{1}{2} = a.\dfrac{1}{2} \Leftrightarrow a = 1 \Rightarrow OI:y = x\). Đường thẳng \((d)\) được viết lại như sau: \(mx + \left( {2 - 3m} \right)y + m - 1 = 0 \Leftrightarrow \left( {2 - 3m} \right)y = - mx + 1 - m\). + Nếu \(m = \dfrac{2}{3}\) thì đường thẳng \((d):x - \dfrac{1}{2} = 0\) song song với trục \(Oy\) nên khoảng cách từ \(O\) đến \((d)\) là \(\dfrac{1}{2}\). + Nếu \(m \ne \dfrac{2}{3}\) đường thẳng \((d)\) có thể viết lại: \(y = \dfrac{m}{{3m - 2}}x + \dfrac{{m - 1}}{{3m - 2}}\). Điều kiện để \((d) \bot OI\) là \(\dfrac{m}{{3m - 2}}.1 = - 1 \Leftrightarrow m = 2 - 3m \Leftrightarrow m = \dfrac{1}{2}\). Khi đó khoảng cách \(OI = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt 2 }}{2}\). Nhận thấy $\dfrac{{\sqrt 2 }}{2}>\dfrac{{1}}{2}$ nên khoảng cách lớn nhất cần tìm là $\dfrac{{\sqrt 2 }}{2}$ khi \(m = \dfrac{1}{2}\). Vậy \(m = \dfrac{1}{2}\) là giá trị cần tìm. Xác định các hệ số \(a,b\) của hàm số \(y = ax + b\) để: Câu 7
Đồ thị của nó đi qua hai điểm \(A\left( {1;3} \right),B\left( {2;4} \right)\)
Đáp án : B Phương pháp giải :
Thay tọa độ các điểm \(A,B\) vào phương trình của đường thẳng rồi biến đổi và tính toán. Lời giải chi tiết :
Thay tọa độ các điểm \(A,B\) vào phương trình của đường thẳng ta được: $\left\{ \begin{array}{l}3 = a + b\,\,\left( 1 \right)\\4 = 2a + b\,\,\left( 2 \right)\end{array} \right.$. Từ \(\left( 1 \right)\) ta có \(b = 3 - a\) . Thay \(b = 3 - a\) vào \(\left( 2 \right)\) ta được \(4 = 2a + 3 - a \Leftrightarrow a = 1 \Rightarrow b = 2\) . Vậy \(a = 1,b = 2\). Câu 8
Đồ thị của nó cắt trục tung tại điểm có tung độ bằng \( - 4\) và cắt trục hoành tại điểm có hoành độ bằng \(2\).
Đáp án : B Phương pháp giải :
+ Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành + Thay tọa độ các điểm vừa tìm được vào hàm số để tìm \(a,b.\) Lời giải chi tiết :
Vì đồ thị cắt trục tung tại điểm có tung độ bằng \( - 4\) nên điểm \(A\left( {0; - 4} \right)\) thuộc đồ thị hàm số, đồ thị cắt trục hoành tại điểm có hoành độ \(2\) nên điểm \(B\left( {2;0} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm \(A\left( {0; - 4} \right)\) vào hàm số \(y = ax + b\) ta được \( - 4 = 0.a + b \Leftrightarrow b = - 4\) \( \Rightarrow y = a.x - 4\) Thay tọa độ điểm \(B\left( {2;0} \right)\) vào hàm số \(y = a.x - 4\) ta được \(0 = a.2 - 4 \Leftrightarrow 2a = 4 \Leftrightarrow a = 2.\) Vậy \(a = 2;b = - 4.\)
Câu 9 :
Cho $2$ đường thẳng $d:y = x + 3;d':y = \dfrac{{ - 2}}{3}x + \dfrac{4}{3}$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $C$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành; $B$ và $D$ lần lượt là giao điểm của $d$ và $d'$ với trục tung. Khi đó diện tích tam giác $CMB$ là:
Đáp án : B Phương pháp giải :
- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng. - Xác định giao điểm 2 đường thẳng đã cho - Tính độ dài các đoạn thẳng cần thiết - Dựng đường cao của tam giác được tạo thành - Tính diện tích các tam giác phụ được tạo thành - Tính diện tích tam giác theo yêu cầu đề bài Lời giải chi tiết :
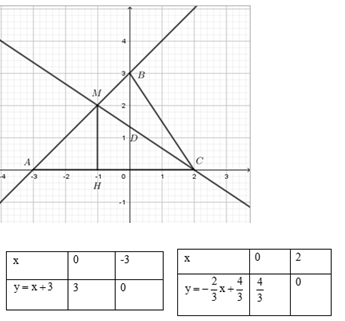 Xét phương trình hoành độ giao điểm: $x + 3 = - \dfrac{2}{3}x + \dfrac{4}{3} \Leftrightarrow 3x + 9 = - 2x + 4 \Leftrightarrow 5x = - 5 \Leftrightarrow x = - 1 \Rightarrow y = 2$ Do đó giao điểm của $2$ đường thẳng đã cho là $M\left( { - 1;2} \right)$ $\begin{array}{l}d \cap Ox = A( - 3;0) \Rightarrow OA = 3\\d' \cap Ox = C(2;0) \Rightarrow OC = 2\\d \cap Oy = B(0;3) \Rightarrow OB = 3\\d' \cap Oy = D\left( {0;\dfrac{4}{3}} \right)\\ \Rightarrow AC = OA + OC = 3 + 2 = 5\\{S_{\Delta ABC}} = \dfrac{1}{2}AC.OB = \dfrac{1}{2}.5.3 = \dfrac{{15}}{2}(dvdt)\end{array}$ Gọi $H$ là hình chiếu của $M$ trên $Ox$ $\begin{array}{l} \Rightarrow MH = |{y_M}| = 2\\{S_{\Delta AMC}} = \dfrac{1}{2}MH.AC = \dfrac{1}{2}.2.5 = 5(dvdt)\\{S_{\Delta BMC}} = {S_{\Delta ABC}} - {S_{\Delta AMC}} = \dfrac{{15}}{2} - 5 = \dfrac{5}{2}(dvdt)\end{array}$
Câu 10 :
Tìm $m$ để đường thẳng $d:y = mx + 1$ cắt đường thẳng $d':y = 2x - 1$ tại $1$ điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$.
Đáp án : B Phương pháp giải :
- Điều kiện để 2 đường thẳng cắt nhau - Tìm tọa độ giao điểm 2 đường thẳng cho trước - Đường phân giác của góc phần tư thứ 2 có phương trình $y = - x$ Lời giải chi tiết :
Ta có: $d \cap d' \Leftrightarrow m \ne 2$ Xét phương trình hoành độ giao điểm của $d$ và $d'$: $\begin{array}{l}mx + 1 = 2x - 1 \Leftrightarrow (m - 2)x = - 2\\ \Rightarrow x = \dfrac{{ - 2}}{{m - 2}} \Rightarrow y = 2.\dfrac{{ - 2}}{{m - 2}} - 1 = \dfrac{{ - m - 2}}{{m - 2}}.\end{array}$ Phương trình đường phân giác góc phần tư thứ $2$ là $y = - x$ Vì $d$ và $d'$ cắt nhau tại $1$ điểm điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$ nên ta có: $\dfrac{{ - m - 2}}{{m - 2}} = - \dfrac{{ - 2}}{{m - 2}} \Leftrightarrow - m - 2 = 2 \Leftrightarrow m = - 4$ (t/m) Vậy $m = - 4$.
Câu 11 :
Có bao nhiêu giá trị nguyên của $m$ để $2$ đường thẳng $d:y = mx - 2;d':y = 2x + 1$ cắt nhau tại điểm có hoành độ là số nguyên.
Đáp án : D Phương pháp giải :
- Điều kiện để 2 đường thẳng cắt nhau - Tìm tọa độ giao điểm 2 đường thẳng - Tìm nghiệm nguyên Lời giải chi tiết :
Ta có: $d \cap d' \Leftrightarrow m \ne 2$. Xét phương trình hoành độ giao điểm của $d$ và $d'$ : $mx - 2 = 2x + 1 \Leftrightarrow (m - 2)x = 3 \Leftrightarrow x = \dfrac{3}{{m - 2}}$ Ta có $x = \dfrac{3}{{m - 2}} \in Z \Leftrightarrow m - 2 \in U(3) = \left\{ { \pm 1; \pm 3} \right\}$ Ta có bảng sau: 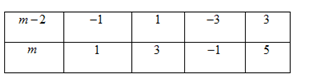 Vậy $m \in \left\{ { - 1;1;3;5} \right\}$.
Câu 12 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Đáp án : C Phương pháp giải :
- Viết phương trình đường thẳng đi qua 2 điểm cho trước - Nhận xét được $MN//AB$ và $AB$ đi qua trung điểm $P$ Lời giải chi tiết :
Giả sử $MN:y = {\rm{ax}} + b$ Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$; $M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$ Do đó $MN:y = - 2{\rm{x}} + 2$. Vì $M,N$ lần lượt là rung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$ Suy ra $AB$ có dạng: $y = - 2x + b'(b' \ne 2)$ Vì $P$ là trung điểm của $AB$ nên $AB$ đi qua $P\left( { - 1; - 1} \right)$ $ \Rightarrow - 1 = - 2( - 1) + b' \Leftrightarrow b' = - 3(t/m)$ Vậy $AB:y = - 2x - 3.$
Câu 13 :
Cho đường thẳng $d:y = ({m^2} - 2m + 2)x + 4$. Tìm $m$ để $d$ cắt $Ox$ tại $A$ và cắt $Oy$ tại $B$ sao cho diện tích tam giác $AOB$ lớn nhất.
Đáp án : A Phương pháp giải :
Tìm tọa độ giao điểm của đường thẳng và 2 trục tọa độ. Biện luận và giải phương trình. Lời giải chi tiết :
$\begin{array}{l}d \cap Oy = \left\{ B \right\}\\x = 0 \Rightarrow y = 4 \Rightarrow B(0;4) \Rightarrow OB = |4| = 4\\d \cap {\rm{Ox}} = \left\{ A \right\}\\y = 0 \Leftrightarrow ({m^2} - 2m + 2)x + 4 = 0 \Leftrightarrow x = \dfrac{{ - 4}}{{{m^2} - 2m + 2}}\\ \Rightarrow A\left( {\dfrac{{ - 4}}{{{m^2} - 2m + 2}};0} \right) \Rightarrow OA = \left| {\dfrac{{ - 4}}{{{m^2} - 2m + 2}}} \right|\end{array}$ \( \Rightarrow OA = \dfrac{4}{{{m^2} - 2m + 2}}\) (vì ${m^2} - 2m + 2 = {(m - 1)^2} + 1 \ge 1\begin{array}{*{20}{c}}{}&{\forall m}\end{array}$) ${S_{\Delta AOB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.4.\dfrac{4}{{{m^2} - 2m + 2}} = \dfrac{8}{{{{(m - 1)}^2} + 1}}$ Hay ${S_{\Delta AOB}} = \dfrac{8}{{{{(m - 1)}^2} + 1}} \le \dfrac{8}{1} = 8$ Dấu “=” xảy ra khi $m - 1 = 0 \Leftrightarrow m = 1$.
Câu 14 :
Cho tam giác $ABC$ có đường thẳng $BC:y = - \dfrac{1}{3}x + 1$ và $A\left( {1,2} \right)$ . Viết phương trình đường cao $AH$ của tam giác $ABC$ .
Đáp án : D Phương pháp giải :
Sử dụng kiến thức - $d \bot d' \Leftrightarrow a.a' = - 1$ - Điểm $M(x_0;y_0)$ thuộc đường thẳng $d:y=ax+b$ khi $y_0=ax_0+b.$ Lời giải chi tiết :
Giả sử $AH:y = {\rm{ax}} + b$ Vì $AH$ là đường cao của tam giác $ABC$ nên $AH$ vuông góc với $BC$ nên: $a.\dfrac{{ - 1}}{3} = - 1 \Leftrightarrow a = 3$ Mặt khác $AH$ đi qua $A\left( {1;2} \right)$ nên ta có: $3.1 + b = 2 \Leftrightarrow b = - 1$ Vậy $AH:y = 3x - 1$.
Câu 15 :
Điểm cố định mà đường thẳng $d:y = \dfrac{{\sqrt k + 1}}{{\sqrt 3 - 1}}x + \sqrt k + 3 \, (k \ge 0)$ luôn đi qua là:
Đáp án : A Phương pháp giải :
$M\left( {{x_0};{y_0}} \right)$ là điểm cố định mà d luôn đi qua$ \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d,\forall m \Leftrightarrow m.A + B = 0,\forall m \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.$ Giải hệ phương trình tìm nghiệm. Lời giải chi tiết :
Gọi $M\left( {{x_0};{y_0}} \right)$ là điểm cố định mà $d$ luôn đi qua. $\begin{array}{l} \Leftrightarrow M\left( {{x_0};{y_0}} \right) \in d\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow {y_0} = \dfrac{{\sqrt k + 1}}{{\sqrt 3 - 1}}{x_0} + \sqrt k + \sqrt 3 \begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k {x_0} + {x_0} + \sqrt {3k} - \sqrt k - \sqrt 3 + 3 - \sqrt 3 {y_0} + {y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \sqrt k ({x_0} + \sqrt 3 - 1) + {x_0} + 3 - \sqrt 3 + (1 - \sqrt 3 ){y_0} = 0\begin{array}{*{20}{c}}{}&{}\end{array}\forall k\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} + \sqrt 3 - 1 = 0\\{x_0} + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ) + (1 - \sqrt 3 ){y_0} + 3 - \sqrt 3 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + 4 - 2\sqrt 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\(1 - \sqrt 3 ){y_0} + {(1 - \sqrt 3 )^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 1 - \sqrt 3 \\{y_0} = - 1 + \sqrt 3 \end{array} \right.\end{array}$ $ \Rightarrow M\left( {1 - \sqrt 3 ;\sqrt 3 - 1} \right)$là điểm cố định mà d luôn đi qua.
Câu 16 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Đáp án : C Phương pháp giải :
- Viết phương trình đường thẳng đi qua 2 điểm cho trước - Nhận xét được $MN//AB$ và $AB$ đi qua trung điểm $P$ Lời giải chi tiết :
Giả sử $MN:y = {\rm{ax}} + b$ Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$; $M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$ Do đó $MN:y = - 2{\rm{x}} + 2$. Vì $M,N$ lần lượt là rung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$ Suy ra $AB$ có dạng: $y = - 2x + b'(b' \ne 2)$ Vì $P$ là trung điểm của $AB$ nên $AB$ đi qua $P\left( { - 1; - 1} \right)$ $ \Rightarrow - 1 = - 2( - 1) + b' \Leftrightarrow b' = - 3(t/m)$ Vậy $AB:y = - 2x - 3.$
Câu 17 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( {1;1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Viết phương trình đường trung trực của đoạn thẳng $AB$.
Đáp án : A Phương pháp giải :
+ Sử dụng kiến thức điểm thuộc đường thẳng để viết phương trình $MN.$ + Sử dụng kiến thức đường trung bình, đường trung trực, điều kiện hai đường thẳng vuông góc và điểm thuộc đường thẳng để viết phương trình đường trung trực của $AB.$ Lời giải chi tiết :
Gọi phương trình đường trung trực của $AB$ là $d:y = mx + n$ và $MN:y = ax + b$ Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$; $M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$ Do đó $MN:y = - 2{\rm{x}} + 2$. Vì $M,N$ lần lượt là trung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$. Vì $d$ là đường trung trực của $AB$ nên $d \bot MN \Rightarrow m( - 2) = - 1 \Leftrightarrow m = \dfrac{1}{2}$ $ \Rightarrow d:y = \dfrac{1}{2}x + n$ Vì $P$ là trung điểm của $AB$ nên \(d\) đi qua $P$ $ \Rightarrow 1 = \dfrac{1}{2}.1 + n \Leftrightarrow n = \dfrac{1}{2}$. Vậy trung trực của $AB$ là : $y = \dfrac{1}{2}x + \dfrac{1}{2}$. Cho hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 5\\mx - y = 4\end{array} \right.\)\(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\) Câu 18
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) trong đó \(x,y\) trái dấu.
Đáp án : A Phương pháp giải :
+ Từ phương trình (1) biểu diễn \(x\) theo \(y.\) + Thế vào phương trình \(\left( 2 \right)\) để được phương trình bậc nhất ẩn \(y.\) + Sử dụng kiến thức \(A.X + B = 0\) có nghiệm duy nhất khi \(A \ne 0.\) + Biến đổi theo yêu cầu \(xy < 0\) để tìm ra điều kiện của \(m.\) Lời giải chi tiết :
Từ phương trình (1) ta có \(x = 2y + 5\). Thay \(x = 2y + 5\) vào phương trình (2) ta được:\(m\left( {2y + 5} \right) - y = 4 \Leftrightarrow \left( {2m - 1} \right).y = 4 - 5m\) (3) Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất. Điều này tương đương với: \(2m - 1 \ne 0 \Leftrightarrow m \ne \dfrac{1}{2}\). Từ đó ta được: \(y = \dfrac{{4 - 5m}}{{2m - 1}}\) và \(x = 5 + 2y = \dfrac{3}{{2m - 1}}\). Ta có: \(x.y = \dfrac{{3\left( {4 - 5m} \right)}}{{{{\left( {2m - 1} \right)}^2}}}\). Do đó \(x.y < 0 \Leftrightarrow 4 - 5m < 0 \Leftrightarrow m > \dfrac{4}{5}\) (thỏa mãn điều kiện) Câu 19
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn \(x = \left| y \right|\).
Đáp án : A Phương pháp giải :
+ Từ phương trình (1) biểu diễn \(x\) theo \(y.\) + Thế vào phương trình \(\left( 2 \right)\) để được phương trình bậc nhất ẩn \(y.\) + Sử dụng kiến thức \(A.X + B = 0\) có nghiệm duy nhất khi \(A \ne 0.\) + Biến đổi theo yêu cầu \[x = \left| y \right|\] để tìm ra điều kiện của \(m.\) Lời giải chi tiết :
Từ phương trình (1) ta có \(x = 2y + 5\). Thay \(x = 2y + 5\) vào phương trình (2) ta được:\(m\left( {2y + 5} \right) - y = 4 \Leftrightarrow \left( {2m - 1} \right).y = 4 - 5m\) (3) Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất. Điều này tương đương với: \(2m - 1 \ne 0 \Leftrightarrow m \ne \dfrac{1}{2}\). Từ đó ta được: \(y = \dfrac{{4 - 5m}}{{2m - 1}}\) và \(x = 5 + 2y = \dfrac{3}{{2m - 1}}\). Ta có: \(x = \left| y \right| \Leftrightarrow \dfrac{3}{{2m - 1}} = \left| {\dfrac{{4 - 5m}}{{2m - 1}}} \right|\) (4) Từ (4) suy ra \(2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\). Với điều kiện \(m > \dfrac{1}{2}\) ta có: \(\left( 4 \right) \Leftrightarrow \left| {4 - 5m} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}4 - 5m = 3\\4 - 5m = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{5}\left( l \right)\\m = \dfrac{7}{5}\end{array} \right.\). Vậy \(m = \dfrac{7}{5}\). Cho đường thẳng \(\left( {{d_1}} \right):y = x + 2\) và đường thẳng \(\left( {{d_2}} \right):y = \left( {2{m^2} - m} \right)x + {m^2} + m\). Câu 20
Tìm \(m\) để \(({d_1})//({d_2})\).
Đáp án : C Phương pháp giải :
Hai đường thẳng \(\left( d \right):y = ax + b;\,\left( {d'} \right):y = a'x + b'\) song song với nhau khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\) Lời giải chi tiết :
Đường thẳng \(({d_1})//({d_2})\) khi và chỉ khi \(\left\{ \begin{array}{l}2{m^2} - m = 1\\{m^2} + m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {m - 1} \right)\left( {2m + 1} \right) = 0\\\left( {m - 1} \right)\left( {m + 2} \right) \ne 0\end{array} \right. \Leftrightarrow m = - \dfrac{1}{2}\). Vậy với \(m = - \dfrac{1}{2}\) thì \(({d_1})//({d_2})\). Câu 21
Gọi \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\). Viết phương trình đường thẳng \(({d_3})\) đi qua \(A\) vuông góc với \(({d_1})\).
Đáp án : A Phương pháp giải :
+ Tìm điểm A. + Sử dụng: Hai đường thẳng \(\left( d \right):y = ax + b;\,\left( {d'} \right):y = a'x + b'\) vuông góc với nhau khi \(a.a' = - 1\). Lời giải chi tiết :
Vì \(A\) là điểm thuộc đường thẳng \(({d_1})\) có hoành độ \(x = 2\) suy ra tung độ điểm \(A\) là \(y = 2 + 2 = 4 \Rightarrow A\left( {2;4} \right)\) . Đường thẳng \(\left( {{d_1}} \right)\) có hệ số góc là \(a = 1\), đường thẳng \(\left( {{d_2}} \right)\) có hệ số góc là \(a' \Rightarrow a'.1 = - 1 \Rightarrow a' = - 1\) . Đường thẳng \(\left( {{d_3}} \right)\) có dạng \(y = - x + b\). Vì \(\left( {{d_3}} \right)\) đi qua \(A\left( {2;4} \right)\) suy ra \(4 = - 2 + b \Rightarrow b = 6\). Vậy đường thẳng \(\left( {{d_3}} \right)\) là \(y = - x + 6\). Câu 22
Khi \(({d_1})//({d_2})\). Hãy tính khoảng cách giữa hai đường thẳng \(({d_1}),\left( {{d_2}} \right)\).
Đáp án : D Phương pháp giải :
Khi \(({d_1})//({d_2})\) thì khoảng cách giữa hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cũng chính là khoảng cách giữa hai điểm \(A,B\) lần lượt thuộc \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) sao cho \(AB \bot ({d_1}),AB \bot \left( {{d_2}} \right)\). Lời giải chi tiết :
Khi \(({d_1})//({d_2})\) thì khoảng cách giữa hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cũng chính là khoảng cách giữa hai điểm \(A,B\) lần lượt thuộc \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) sao cho \(AB \bot ({d_1}),AB \bot \left( {{d_2}} \right)\). Hình vẽ: 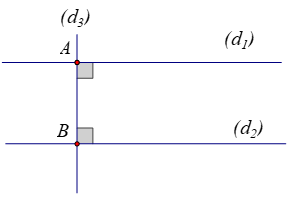 Gọi \(B\) là giao điểm của đường thẳng \(({d_3})\) và \(({d_2})\). Phương trình hoành độ giao điểm của \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right)\) là: \( - x + 6 = x - \dfrac{1}{4} \Leftrightarrow x = \dfrac{{25}}{8} \Rightarrow y = \dfrac{{23}}{8} \Rightarrow B\left( {\dfrac{{25}}{8};\dfrac{{23}}{8}} \right)\). Vậy độ dài đoạn thẳng \(AB\) là: \(AB = \sqrt {{{\left( {\dfrac{{25}}{8} - 2} \right)}^2} + {{\left( {\dfrac{{23}}{8} - 4} \right)}^2}} = \dfrac{{9\sqrt 2 }}{8}\). Câu 23
Tính diện tích tam giác \(OMN\) với \(M,N\) lần lượt là giao điểm của \(({d_1})\) với các trục tọa độ \(Ox,Oy\).
Đáp án : C Phương pháp giải :
+ Tìm tọa độ M, N. Tính độ dài \(OM;ON\) sau đó tính diện tích tam giác \(OMN.\) Lời giải chi tiết :
Gọi \(M,N\) lần lượt là giao điểm của đường thẳng \(\left( {{d_1}} \right)\) với các trục tọa độ \(Ox,Oy\). Ta có: Cho \(y = 0 \Rightarrow x = - 2 \Rightarrow A\left( { - 2;0} \right)\), cho \(y = 0 \Rightarrow x = - 2 \Rightarrow N\left( { - 2;0} \right)\). Từ đó suy ra \(OM = ON = 2\). Tam giác $OMN$ vuông cân tại \(O\) nên \({S_{OMN}} = \dfrac{1}{2}OM.ON = 2\) ( đvdt).
Câu 24 :
Cho $2$ đường thẳng: $d:y = x + 3;d':y = \dfrac{{ - 2}}{3}x + \dfrac{4}{3}$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $C$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành; $B$ và $D$ lần lượt là giao điểm của $d$ và $d'$ với trục tung. Khi đó diện tích tam giác $CMB$ là:
Đáp án : B Phương pháp giải :
- Lập bảng giá trị để xác định 2 điểm thuộc đường thẳng. - Xác định giao điểm 2 đường thẳng đã cho - Tính độ dài các đoạn thẳng cần thiết - Dựng đường cao của tam giác được tạo thành - Tính diện tích các tam giác phụ được tạo thành - Tính diện tích tam giác theo yêu cầu đề bài. Lời giải chi tiết :
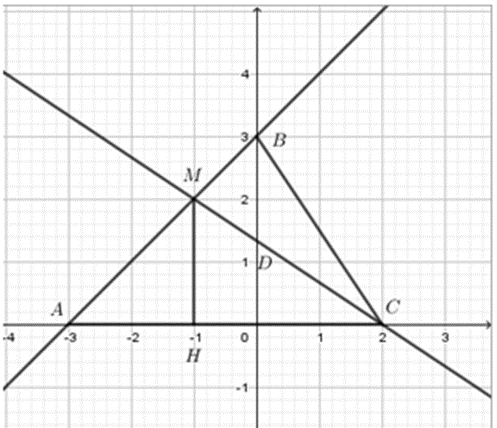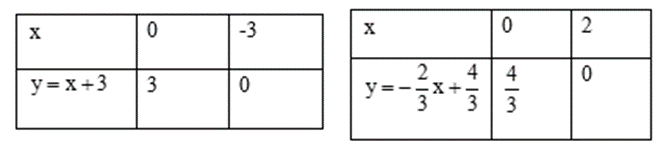  Xét phương trình hoành độ giao điểm: $x + 3 = - \dfrac{2}{3}x + \dfrac{4}{3} \Leftrightarrow 3x + 9 = - 2x + 4 \Leftrightarrow 5x = - 5 \Leftrightarrow x = - 1 \Rightarrow y = 2$ Do đó giao điểm của $2$ đường thẳng đã cho là $M\left( { - 1;2} \right)$ $\begin{array}{l}d \cap Ox = A( - 3;0) \Rightarrow OA = 3\\d' \cap Ox = C(2;0) \Rightarrow OC = 2\\d \cap Oy = B(0;3) \Rightarrow OB = 3\\d' \cap Oy = D\left( {0;\dfrac{4}{3}} \right)\\ \Rightarrow AC = OA + OC = 3 + 2 = 5\\{S_{\Delta ABC}} = \dfrac{1}{2}AC.OB = \dfrac{1}{2}.5.3 = \dfrac{{15}}{2}(dvdt)\end{array}$ Gọi $H$ là hình chiếu của $M$ trên $Ox$ $\begin{array}{l} \Rightarrow MH = |{y_M}| = 2\\{S_{\Delta AMC}} = \dfrac{1}{2}MH.AC = \dfrac{1}{2}.2.5 = 5(dvdt)\\{S_{\Delta BMC}} = {S_{\Delta ABC}} - {S_{\Delta AMC}} = \dfrac{{15}}{2} - 5 = \dfrac{5}{2}(dvdt)\end{array}$ Cho đường thẳng: \(mx + \left( {2 - 3m} \right)y + m - 1 = 0\) \((d)\). Câu 25
Tìm điểm cố định \(I\) mà đường thẳng \((d)\) luôn đi qua.
Đáp án : A Phương pháp giải :
Đưa về phương trình bậc nhất ẩn \(m\) là \(am + b = 0\) đúng với mọi \(m \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 0\end{array} \right.\) Lời giải chi tiết :
Gọi \(I\left( {{x_0};{y_0}} \right)\) là điểm cố định mà đường thẳng \((d)\) luôn đi qua với mọi \(m\) khi đó ta có: \(m{x_0} + \left( {2 - 3m} \right){y_0} + m - 1 = 0\) với mọi \(m\) \( \Leftrightarrow m\left( {{x_0} - 3{y_0} + 1} \right) + 2{y_0} - 1 = 0\) với mọi \(m\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_0} - 3{y_0} + 1 = 0\\2{y_0} - 1 = 0\end{array} \right.\). Hay\(\left\{ \begin{array}{l}{x_0} = \dfrac{1}{2}\\{y_0} = \dfrac{1}{2}\end{array} \right. \Leftrightarrow I\left( {\dfrac{1}{2};\dfrac{1}{2}} \right)\). Câu 26
Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \((d)\) là lớn nhất.
Đáp án : B Phương pháp giải :
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên đường thẳng \((d)\). Ta có: \(OH \le OI\) suy ra \(OH\) lớn nhất bằng \(OI\) khi và chỉ khi \(H \equiv I \Leftrightarrow OI \bot (d)\). Lời giải chi tiết :
Gọi \(H\) là hình chiếu vuông góc của \(O\) lên đường thẳng \((d)\). Ta có: \(OH \le OI\) suy ra \(OH\) lớn nhất bằng \(OI\) khi và chỉ khi \(H \equiv I \Leftrightarrow OI \bot (d)\). Đường thẳng qua \(O\) có phương trình: \(y = ax\) do \(I\left( {\dfrac{1}{2};\dfrac{1}{2}} \right) \in OI \Rightarrow \dfrac{1}{2} = a.\dfrac{1}{2} \Leftrightarrow a = 1 \Rightarrow OI:y = x\) Đường thẳng \((d)\) được viết lại như sau: \(mx + \left( {2 - 3m} \right)y + m - 1 = 0 \Leftrightarrow \left( {2 - 3m} \right)y = - mx + 1 - m\). + Đế ý rằng với \(m = \dfrac{2}{3}\) thì đường thẳng \((d):x - \dfrac{1}{2} = 0\) song song với trục \(Oy\) nên khoảng cách từ \(O\) đến \((d)\) là \(\dfrac{1}{2}\). + Nếu \(m \ne \dfrac{2}{3}\) đường thẳng \((d)\) có thể viết lại: \(y = \dfrac{m}{{3m - 2}}x + \dfrac{{m - 1}}{{3m - 2}}\). Điều kiện để \((d) \bot OI\) là \(\dfrac{m}{{3m - 2}}.1 = - 1 \Leftrightarrow m = 2 - 3m \Leftrightarrow m = \dfrac{1}{2}\). Khi đó khoảng cách \(OI = \sqrt {{{\left( {\dfrac{1}{2}} \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}} = \dfrac{{\sqrt 2 }}{2}\). Vậy \(m = \dfrac{1}{2}\) là giá trị cần tìm. Xác định các hệ số \(a,b\) của hàm số \(y = ax + b\) để: Câu 27
Đồ thị của nó đi qua hai điểm \(A\left( {1;3} \right),B\left( {2;4} \right)\):
Đáp án : B Phương pháp giải :
Thay tọa độ các điểm \(A,B\) vào phương trình của đường thẳng rồi biến đổi và tính toán. Lời giải chi tiết :
Thay tọa độ các điểm \(A,B\) vào phương trình của đường thẳng ta được: $\left\{ \begin{array}{l}3 = a + b\,\,\left( 1 \right)\\4 = 2a + b\,\,\left( 2 \right)\end{array} \right.$ Từ \(\left( 1 \right)\) ta có \(b = 3 - a\) . Thay \(b = 3 - a\) vào \(\left( 2 \right)\) ta được: \(4 = 2a + 3 - a \Leftrightarrow a = 1 \Rightarrow b = 2\) . Vậy \(a = 1,b = 2\). Câu 28
Đồ thị của nó cắt trục tung tại điểm có tung độ bằng \( - 4\) và cắt trục hoành tại điểm có hoành độ bằng \(2\).
Đáp án : B Phương pháp giải :
+ Tìm tọa độ giao điểm của đồ thị hàm số với trục tung và trục hoành. + Thay tọa độ các điểm vừa tìm được vào hàm số để tìm \(a,b.\) Lời giải chi tiết :
Vì đồ thị cắt trục tung tại điểm có tung độ bằng \( - 4\) nên điểm \(A\left( {0; - 4} \right)\) thuộc đồ thị hàm số, đồ thị cắt trục hoành tại điểm ó hoành độ \(2\) nên điểm \(B\left( {2;0} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm \(A\left( {0; - 4} \right)\) vào hàm số \(y = ax + b\) ta được: \( - 4 = 0.a + b \Leftrightarrow b = - 4\) \( \Rightarrow y = a.x - 4\) Thay tọa độ điểm \(B\left( {2;0} \right)\) vào hàm số \(y = a.x - 4\) ta được: \(0 = a.2 - 4 \Leftrightarrow 2a = 4 \Leftrightarrow a = 2.\) Vậy \(a = 2;b = - 4.\) Cho hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 5\\mx - y = 4\end{array} \right.\)\(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\) Câu 29
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) trong đó $x,y$ trái dấu.
Đáp án : A Phương pháp giải :
+ Từ phương trình (1) biểu diễn \(x\) theo \(y.\) + Thế vào phương trình \(\left( 2 \right)\) để được phương trình bậc nhất ẩn \(y.\) + Sử dụng kiến thức \(A.X + B = 0\) có nghiệm duy nhất khi \(A \ne 0.\) + Biến đổi theo yêu cầu \(xy < 0\) để tìm ra điều kiện của \(m.\) Lời giải chi tiết :
Từ phương trình (1) ta có \(x = 2y + 5\). Thay \(x = 2y + 5\) vào phương trình (2) ta được:\(m\left( {2y + 5} \right) - y = 4 \Leftrightarrow \left( {2m - 1} \right).y = 4 - 5m\) (3) Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất. Điều này tương đương với: \(2m - 1 \ne 0 \Leftrightarrow m \ne \dfrac{1}{2}\). Từ đó ta được: \(y = \dfrac{{4 - 5m}}{{2m - 1}}\) và \(x = 5 + 2y = \dfrac{3}{{2m - 1}}\). Ta có: \(x.y = \dfrac{{3\left( {4 - 5m} \right)}}{{{{\left( {2m - 1} \right)}^2}}}\). Do đó \(x.y < 0 \Leftrightarrow 4 - 5m < 0 \Leftrightarrow m > \dfrac{4}{5}\) (thỏa mãn điều kiện). Câu 30
Tìm \(m\) để hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right)\) thỏa mãn $x = \left| y \right|$.
Đáp án : A Phương pháp giải :
+ Từ phương trình (1) biểu diễn \(x\) theo \(y.\) + Thế vào phương trình \(\left( 2 \right)\) để được phương trình bậc nhất ẩn \(y.\) + Sử dụng kiến thức \(A.X + B = 0\) có nghiệm duy nhất khi \(A \ne 0.\) + Biến đổi theo yêu cầu $x = \left| y \right|$ để tìm ra điều kiện của \(m.\) Lời giải chi tiết :
Từ phương trình (1) ta có: \(x = 2y + 5\). Thay \(x = 2y + 5\) vào phương trình (2) ta được:\(m\left( {2y + 5} \right) - y = 4 \Leftrightarrow \left( {2m - 1} \right).y = 4 - 5m\) (3) Hệ có nghiệm duy nhất khi và chỉ khi (3) có nghiệm duy nhất. Điều này tương đương với: \(2m - 1 \ne 0 \Leftrightarrow m \ne \dfrac{1}{2}\). Từ đó ta được: \(y = \dfrac{{4 - 5m}}{{2m - 1}}\) và \(x = 5 + 2y = \dfrac{3}{{2m - 1}}\). Ta có: \(x = \left| y \right| \Leftrightarrow \dfrac{3}{{2m - 1}} = \left| {\dfrac{{4 - 5m}}{{2m - 1}}} \right|\) (4) Từ (4) suy ra: \(2m - 1 > 0 \Leftrightarrow m > \dfrac{1}{2}\). Với điều kiện: \(m > \dfrac{1}{2}\) ta có: \(\left( 4 \right) \Leftrightarrow \left| {4 - 5m} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}4 - 5m = 3\\4 - 5m = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{5}\left( l \right)\\m = \dfrac{7}{5}\end{array} \right.\). Vậy \(m = \dfrac{7}{5}\). Cho hệ phương trình: \(\left\{ \begin{array}{l}x + my = m + 1\\mx + y = 3m - 1\end{array} \right.\) \(\begin{array}{l}\left( 1 \right)\\\left( 2 \right)\end{array}\)
Câu 31
Tìm số nguyên \(m\) sao cho hệ phương trình có nghiệm duy nhất \(\left( {x,y} \right)\) mà $x,y$ đều là số nguyên.
Đáp án : C Phương pháp giải :
+ Từ phương trình (2) biểu diễn \(y\) theo \(x.\) + Thế vào phương trình \(\left( 1 \right)\) để được phương trình bậc nhất ẩn \(x.\) + Sử dụng kiến thức \(A.X + B = 0\) có nghiệm duy nhất khi \(A \ne 0.\) + Biến đổi theo yêu cầu $x;y \in Z$ để tìm ra điều kiện của \(m.\) Lời giải chi tiết :
Từ phương trình (2) ta có \(y = 3m - 1 - mx\). Thay vào phương trình (1) ta được:\(x + m\left( {3m - 1 - mx} \right) = m + 1 \Leftrightarrow \left( {{m^2} - 1} \right)x = 3{m^2} - 2m - 1\) (3) Hệ có nghiệm duy nhất khi và chỉ khi phương trình (3) có nghiệm duy nhất, tức là \({m^2} - 1 \ne 0 \Leftrightarrow m \ne \pm 1\). Khi đó: \(\left\{ \begin{array}{l}x = \dfrac{{3{m^2} - 2m - 1}}{{{m^2} - 1}} = \dfrac{{\left( {m - 1} \right)\left( {3m + 1} \right)}}{{\left( {m - 1} \right).\left( {m + 1} \right)}} = \dfrac{{3m + 1}}{{m + 1}}\\y = 3m - 1 - m.\dfrac{{3m + 1}}{{m + 1}} = \dfrac{{m - 1}}{{m + 1}}\end{array} \right.\) Hay \(\left\{ \begin{array}{l}x = \dfrac{{3m + 1}}{{m + 1}} = 3 - \dfrac{2}{{m + 1}}\\y = \dfrac{{m - 1}}{{m + 1}} = 1 - \dfrac{2}{{m + 1}}\end{array} \right.\) Vậy \(x,y\) nguyên khi và chỉ khi \(\dfrac{2}{{m + 1}}\) nguyên. Do đó \(m + 1\) chỉ có thể là \( - 2; - 1;1;2\). Vậy \(m \in \left\{ { - 3; - 2;0} \right\}\) (thỏa mãn) hoặc \(m = 1\) (loại). Câu 32
Trong trường hợp hệ có nghiệm duy nhất \(\left( {x;y} \right)\) thì điểm \(M\left( {x;y} \right)\) luôn chạy trên đường thẳng nào dưới đây?
Đáp án : C Phương pháp giải :
+ Tìm \(m\) để hệ phương trình có nghiệm duy nhất (sử dụng kết quả câu trước ) + Tìm \(x;y\) theo \(m\) và biến đổi để có hệ thức của \(x;y\) độc lập với \(m.\) Lời giải chi tiết :
Theo câu trước ta có hệ có nghiệm duy nhất khi và chỉ khi \(m \ne \pm 1\). Khi đó: \(\left\{ \begin{array}{l}x = \dfrac{{3m + 1}}{{m + 1}} = 3 - \dfrac{2}{{m + 1}}\\y = \dfrac{{m - 1}}{{m + 1}} = 1 - \dfrac{2}{{m + 1}}\end{array} \right.\) Suy ra: $x - y = 3 - \dfrac{2}{{m + 1}} - \left( {1 - \dfrac{2}{{m + 1}}} \right) = 2$ Vậy điểm \(M\left( {x;y} \right)\) luôn chạy trên đường thẳng cố định có phương trình \(y = x - 2\). Câu 33
Tìm \(m\) để hệ trên có nghiệm duy nhất sao cho \(x.y\) đạt giá trị nhỏ nhất.
Đáp án : B Phương pháp giải :
+ Tìm \(m\) để hệ phương trình có nghiệm duy nhất (sử dụng kết quả câu trước). + Tìm \(x;y\) theo \(m\) và biến đổi để có \(x.y\) nhỏ nhất. Lời giải chi tiết :
Theo câu trước ta có hệ có nghiệm duy nhất khi và chỉ khi \(m \ne \pm 1\). Khi đó: \(\left\{ \begin{array}{l}x = \dfrac{{3m + 1}}{{m + 1}} = 3 - \dfrac{2}{{m + 1}}\\y = \dfrac{{m - 1}}{{m + 1}} = 1 - \dfrac{2}{{m + 1}}\end{array} \right.\) Suy ra: \(y = x - 2.\) Nên \(xy = x.\left( {x - 2} \right) = {x^2} - 2x + 1 - 1 = {\left( {x - 1} \right)^2} - 1 \ge - 1\) Dấu bằng xảy ra khi và chỉ khi: \(x = 1 \Leftrightarrow 3 - \dfrac{2}{{m + 1}} = 1 \Leftrightarrow \dfrac{2}{{m + 1}} = 2 \Leftrightarrow m + 1 = 1 \Leftrightarrow m = 0\). Vậy với \(m = 0\) thì \(x.y\) đạt giá trị nhỏ nhất.
Câu 34 :
Tìm $m$ để đường thẳng $d:y = mx + 1$ cắt đường thẳng $d':y = 2x - 1$ tại $1$ điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$.
Đáp án : B Phương pháp giải :
- Điều kiện để 2 đường thẳng cắt nhau. - Tìm tọa độ giao điểm 2 đường thẳng cho trước. - Đường phân giác của góc phần tư thứ 2 có phương trình $y = - x$. Lời giải chi tiết :
Ta có: $d \cap d' \Leftrightarrow m \ne 2$ Xét phương trình hoành độ giao điểm của $d$ và $d'$: $\begin{array}{l}mx + 1 = 2x - 1 \Leftrightarrow (m - 2)x = - 2\\ \Rightarrow x = \dfrac{{ - 2}}{{m - 2}} \Rightarrow y = 2.\dfrac{{ - 2}}{{m - 2}} - 1 = \dfrac{{ - m - 2}}{{m - 2}}.\end{array}$ Phương trình đường phân giác góc phần tư thứ $2$ là $y = - x$ Vì $d$ và $d'$ cắt nhau tại $1$ điểm điểm thuộc đường phân giác góc phần tư thứ $II$ và thứ $IV$ nên ta có: $\dfrac{{ - m - 2}}{{m - 2}} = - \dfrac{{ - 2}}{{m - 2}} \Leftrightarrow - m - 2 = 2 \Leftrightarrow m = - 4$(t/m) Vậy $m = - 4$.
Câu 35 :
Giá trị nguyên có thể có của $m$ để $2$ đường thẳng $d:y = mx - 2;d':y = 2x + 1$ cắt nhau tại điểm có hoành độ là số nguyên.
Đáp án : D Phương pháp giải :
- Điều kiện để 2 đường thẳng cắt nhau. - Tìm tọa độ giao điểm 2 đường thẳng. - Tìm nghiệm nguyên. Lời giải chi tiết :
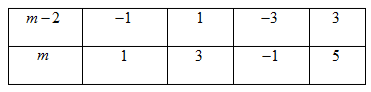
Ta có: $d \cap d' \Leftrightarrow m \ne 2$. Xét phương trình hoành độ giao điểm của $d$ và $d'$: $mx - 2 = 2x + 1 \Leftrightarrow (m - 2)x = 3 \Leftrightarrow x = \dfrac{3}{{m - 2}}$ Ta có: $x = \dfrac{3}{{m - 2}} \in Z \Leftrightarrow m - 2 \in U(3) = \left\{ { \pm 1; \pm 3} \right\}$. Ta có bảng sau:
Vậy $m \in \left\{ { - 1;1;3;5} \right\}$.
Câu 36 :
Cho $M\left( {0;2} \right),N\left( {1;0} \right),P\left( { - 1; - 1} \right)$ lần lượt là trung điểm của các cạnh $BC,CA$ và $AB$ của tam giác $ABC$ . Phương trình đường thẳng $AB$ của tam giác $ABC$ là:
Đáp án : C Phương pháp giải :
- Viết phương trình đường thẳng đi qua 2 điểm cho trước. - Nhận xét được $MN//AB$ và $AB$ đi qua trung điểm $P$. Lời giải chi tiết :
Giả sử: $MN:y = {\rm{ax}} + b$ Ta có: $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a = - b$; $M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a = - 2$ Do đó: $MN:y = - 2{\rm{x}} + 2$. Vì $M,N$ lần lượt là trung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$. Suy ra: $AB$ có dạng: $y = - 2x + b'(b' \ne 2)$ Vì $P$ là trung điểm của $AB$ nên $AB$ đi qua $P\left( { - 1; - 1} \right)$. $ \Rightarrow - 1 = - 2( - 1) + b' \Leftrightarrow b' = - 3(t/m)$ Vậy $AB:y = - 2x - 3.$
|
