Trắc nghiệm Bài 5: Ứng dụng thực tế tỉ số lượng giác của góc nhọn Toán 9Đề bài
Câu 1 :
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
Câu 2 :
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
Câu 3 :
Một cột đèn điện $AB$ cao $6m$ có bóng in trên mặt đất là $AC$ dài $3,5m.$ Hãy tính góc $\widehat {BCA}$ (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
Câu 4 :
Một cây tre cau $9m$ bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc $3m$. Hỏi điểm gãy cách gốc bao nhiêu?
Câu 5 :
Nhà bạn Minh có một chiếc thang dài $4\,m$. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là ${65^0}$ (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
Câu 6 :
Một máy bay đang bay ở độ cao $10km$ so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là ${15^0}$ thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến hai chữ số phần thập phân)
Câu 7 :
Một cái cây bị sét đánh trúng thân cây làm thân cây ngả xuống đất, tạo với mặt đất một góc là ${40^0}$. Biết rằng khúc cây còn đứng cao $1\,m$ . Tính chiều cao lúc đầu của cây.
Câu 8 :
Một chiếc máy bay đang bay lên với vận tốc $500\,km/h$ . Đường bay lên tạo với phương ngang một góc ${30^0}$. Hỏi sau $1,2$ phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu?
Câu 9 :
Một khúc sông rộng khoảng $250m$. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ?
Câu 10 :
Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau $100m$ thì nhìn thấy một chiếc diều ( ở vị trí $C$ giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Trung là ${50^0}$ và góc ''nâng'' để nhìn thấy diều ở vị trí của Dũng là ${40^0}$ . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Câu 11 :
Hai bạn học sinh $A$ và $B$ đang đứng ở mặt đất bằng phẳng, cách nhau 80 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí $C$ nằm trên tia $AB$ và $AC>AB$). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của $B$ là \(55^\circ \) góc ''nâng'' để nhìn thấy máy bay ở vị trí của $A$ là $40^\circ $. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Câu 12 :
Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này dưới một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai):
Câu 13 :
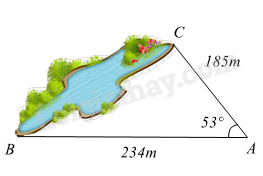
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
Lời giải và đáp án
Câu 1 :
Một cột đèn có bóng trên mặt đất dài $7,5m.$ Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng ${42^0}.$ Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
Đáp án : A Lời giải chi tiết :
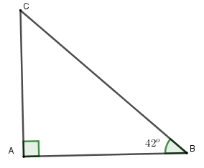 Ta có chiều cao cột đèn là $AC$; $AB = 7,5\,m$ và $\widehat {ACB} = 42^\circ $ Xét tam giác $ACB$ vuông tại $A$ có $AC = AB.\tan B = 7,5.\tan 42^\circ \approx 6,753\,\,m$ Vậy cột đèn cao $6,753\,m$
Câu 2 :
Một cầu trượt trong công viên có độ dốc là ${28^0}$ và có độ cao là $2,1m.$Tính độ dài của mặt cầu trượt (làm tròn đến chữ số thập phân thứ hai).
Đáp án : D Lời giải chi tiết :
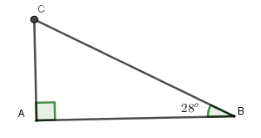 Ta có độ dài của mặt cầu trượt là $AB$; $AC = 2,1\,m$ và $\widehat {ABC} = 28^\circ $ Xét tam giác $ACB$ vuông tại $A$ có $BC = AB:\sin B = 2,1:\sin 28^\circ \simeq 4,47\,m$ Vậy độ dài của mặt cầu trượt là $4,47\,m.$
Câu 3 :
Một cột đèn điện $AB$ cao $6m$ có bóng in trên mặt đất là $AC$ dài $3,5m.$ Hãy tính góc $\widehat {BCA}$ (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
Đáp án : C Phương pháp giải :
Sử dụng tỉ số lượng giác của góc nhọn từ đó suy ra góc. Lời giải chi tiết :
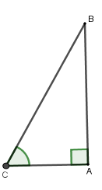 Ta có $\tan C = \dfrac{{AB}}{{AC}} = \dfrac{6}{{3,5}} = \dfrac{{12}}{7} \Rightarrow \widehat C \approx 59^\circ 45'$
Câu 4 :
Một cây tre cau $9m$ bị gió bão làm gãy ngang thân, ngọn cây chạm đất cách gốc $3m$. Hỏi điểm gãy cách gốc bao nhiêu?
Đáp án : C Phương pháp giải :
Sử dụng định lý Py-ta-go: "Tổng bình phương hai cạnh góc vuông bằng bình phương cạnh huyền" Lời giải chi tiết :
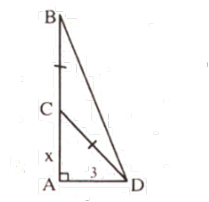 Giả sử $AB$ là độ cao của cây tre, $C$ là điểm gãy. Đặt $AC = x (0<x<9)\Leftrightarrow CB = CD = 9-x$. Vì $\Delta ACD$ vuông tại $A$ Suy ra \(A{C^2} + A{D^2} = C{D^2}\) \(\Leftrightarrow {x^2} + {3^2} = {\left( {9 - x} \right)^2} \) \(\Leftrightarrow x = 4\) (TM) Vậy điểm gãy cách gốc cây $4m.$
Câu 5 :
Nhà bạn Minh có một chiếc thang dài $4\,m$. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là ${65^0}$ (tức là đảm bảo thang không bị đổ khi sử dụng). (làm tròn đến chữ số thập phân thứ hai)
Đáp án : D Lời giải chi tiết :
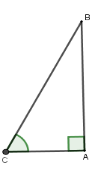 Ta có $BC = 4\,\,m;\widehat C = 65^\circ $. Xét $\Delta ABC$ vuông tại $A$ có $AC = BC.\cos \widehat C = 4.\cos 65^\circ \simeq 1,69\,\,m$.
Câu 6 :
Một máy bay đang bay ở độ cao $10km$ so với mặt đất, muốn hạ cánh xuống sân bay. Để đường bay và mặt đất hợp thành một góc an toàn là ${15^0}$ thì phi công phải bắt đầu hạ cánh từ vị trí cách sân bay bao xa? ( làm tròn kết quả đến hai chữ số phần thập phân)
Đáp án : A Lời giải chi tiết :
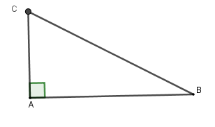 Từ giả thiết suy ra $AC = 10\,\,km;\,\,\widehat B = 15^\circ $. Xét tam giác $\Delta ABC$ vuông tại $A$ có $AB = AC.\cot B = 10.\cot 15^\circ \approx 37,32\,km$
Câu 7 :
Một cái cây bị sét đánh trúng thân cây làm thân cây ngả xuống đất, tạo với mặt đất một góc là ${40^0}$. Biết rằng khúc cây còn đứng cao $1\,m$ . Tính chiều cao lúc đầu của cây.
Đáp án : D Lời giải chi tiết :
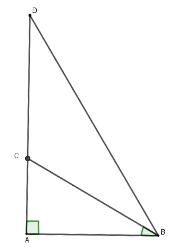 Từ giả thiết ta có chiều dài ban đầu của cây là $AD$; sau khi bị sét đánh thì cây còn lại $AC = 1\,\,m;\widehat {CBA} = 40^\circ $và $CD = CB$. Xét tam giác $\Delta ABC$ vuông tại $A$ có $BC = \dfrac{{AC}}{{\sin 40^\circ }} = 1,56\,m$ nên $CD=1,56\,m$ Suy ra $AD = AC + CD $ $= 1 + 1,56 = 2,56\,m$. Vậy cây cao $2,56\,m$.
Câu 8 :
Một chiếc máy bay đang bay lên với vận tốc $500\,km/h$ . Đường bay lên tạo với phương ngang một góc ${30^0}$. Hỏi sau $1,2$ phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu?
Đáp án : B Lời giải chi tiết :
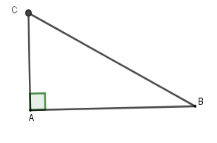 Đổi $1,2' = \dfrac{1}{{50}}h$. Sau $1,2$ phút máy bay ở $C$. Quãng đường bay được là $BC = 500.\dfrac{1}{{50}} = 10\,km$ và $\widehat B = 30^\circ $ Nên $AC = BC.\sin 30^\circ = 5\,km$. Vậy máy bay đạt được độ cao là $5\,km$ sau $1,2$ phút.
Câu 9 :
Một khúc sông rộng khoảng $250m$. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ?
Đáp án : C Phương pháp giải :
Sử dụng tỉ số lượng giác của góc nhọn để suy ra góc. Lời giải chi tiết :
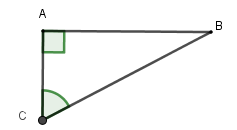 Ta có khúc sông $AC = 250\,m$, quãng đường thuyền đi là $BC = 320\,m$ Góc lệch là $\widehat C$. Ta có $\cos C = \dfrac{{AC}}{{BC}} = \dfrac{{250}}{{320}} \Rightarrow \widehat C \approx 38^\circ 37'$ Vậy góc lệch là $38^\circ 37'$.
Câu 10 :
Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau $100m$ thì nhìn thấy một chiếc diều ( ở vị trí $C$ giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Trung là ${50^0}$ và góc ''nâng'' để nhìn thấy diều ở vị trí của Dũng là ${40^0}$ . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Đáp án : B Lời giải chi tiết :
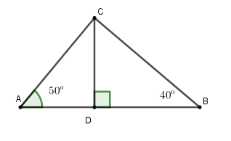 Độ cao của diều là $CD$, độ dài $AB = 100\,m$. Trung đứng ở $A$ , Dũng đứng ở $B$ . Gọi $AD = x\left( {0 < x < 100} \right)$ $ \Rightarrow BD = 100 - x$ Xét $\Delta ACD$ vuông tại $D$ ta có $CD = AD.\tan A = x.\tan 50^\circ $ Xét $\Delta ABD$ vuông tại $D$ ta có $CD = BD.{\mathop{\rm tanB}\nolimits}$ $ = \left( {100 - x} \right).\tan 40^\circ $ Nên $x.\tan 50^\circ = \left( {100 - x} \right)\tan 40^\circ $ $ \Rightarrow x \approx 41,32$ (thoả mãn) $ \Rightarrow CD = 41,32.\tan50^\circ \approx 49,24\,m$ Vậy độ cao của diều lúc đó so với mặt đất là $49,24\,m$.
Câu 11 :
Hai bạn học sinh $A$ và $B$ đang đứng ở mặt đất bằng phẳng, cách nhau 80 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí $C$ nằm trên tia $AB$ và $AC>AB$). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của $B$ là \(55^\circ \) góc ''nâng'' để nhìn thấy máy bay ở vị trí của $A$ là $40^\circ $. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Đáp án : A Lời giải chi tiết :
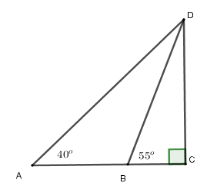 Độ cao của máy bay là $CD$, độ dài $AB=80\,m$. Gọi $BC = x (x>0)\Rightarrow AC = 80 + x$ Xét tam giác $BDC$ vuông tại $C$ có $CD = x.\tan 55^\circ $ Xét tam giác $ADC$ vuông tại $C$ có $CD = \left( {80 + x} \right).\tan 40^\circ $ Suy ra $x\tan 55^\circ = \left( {80 + x} \right)\tan 40^\circ $ $\Leftrightarrow x \approx 113,96\,m$ $ \Rightarrow CD = 113,96.\tan 55^\circ \approx 162,75\,m$ Vậy độ cao của máy bay so với mặt đất là $162,75\,m$.
Câu 12 :
Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này dưới một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai):
Đáp án : D Phương pháp giải :
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài. Lời giải chi tiết :
Xét \(\Delta CDE\) vuông tại \(E\) ta có: \(CE = DE.\tan {55^0} = 6.\tan {55^0} \approx 8,57\,m.\) \( \Rightarrow \) Chiều cao của cây là: \(BC = CE + BE = 8,57 + 1,6 = 10,17\,\,m.\)
Câu 13 :
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
Đáp án : C Phương pháp giải :
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\) Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\) Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ACD\) vuông tại \(D\) ta có: \(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow BD = AB - AD.\end{array}\) Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\) Lời giải chi tiết :
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\) Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\) Áp dụng tỉ số lượng giác của góc nhọn trong \(\Delta ACD\) vuông tại \(D\) ta có: \(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\ \Rightarrow CD = 185.\sin {53^0}.\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow AD = 185.\cos {53^0}.\\ \Rightarrow BD = AB - AD = 234 - 185.\cos {53^0}.\end{array}\) Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\) \(\begin{array}{l}B{C^2} = B{D^2} + C{D^2} = {\left( {234 - 185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {\left( {185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {185^2}\\ \Leftrightarrow B{C^2} \approx 36875,86\\ \Rightarrow BC \approx 192\,m.\end{array}\)
|














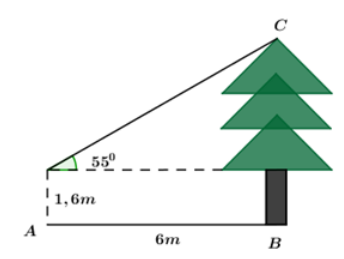
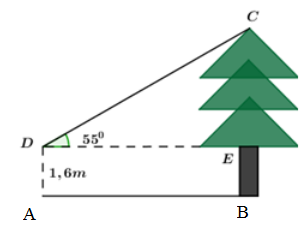 Đặt các điểm \(D,\,\,E\) như hình vẽ.
Đặt các điểm \(D,\,\,E\) như hình vẽ.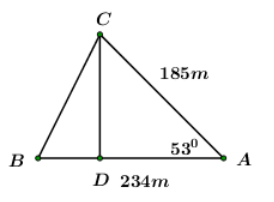





Danh sách bình luận