Trắc nghiệm Bài 7,8 Vị trí tương đối của hai đường tròn Toán 9Đề bài
Câu 1 :
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là
Câu 2 :
Cho hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$ với $R > r$ cắt nhau tại hai điểm phân biệt và $OO' = d$. Chọn khẳng định đúng?
Câu 3 :
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
Câu 4 :
Cho hai đường tròn \(\left( {I;7cm} \right)\) và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là:
Cho đường tròn $\left( O \right)$ bán kính $OA$ và đường tròn $\left( {O'} \right)$ đường kính $OA$. Câu 5
Vị trí tương đối của hai đường tròn là
Câu 6
Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ tại $C$. Khi đó
Cho hai đường tròn $\left( {{O_1}} \right)$ và $\left( {{O_2}} \right)$ tiếp xúc ngoài tại $A$ và một đường thẳng $d$ tiếp xúc với $\left( {{O_1}} \right);\left( {{O_2}} \right)$ lần lượt tại $B,C$. Câu 7
Tam giác $ABC$ là
Câu 8
Lấy $M$ là trung điểm của $BC$. Chọn khẳng định sai?
Câu 9 :
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
Cho nửa đường tròn $\left( O \right)$, đường kính $AB$. Vẽ nửa đường tròn tâm $O'$ đường kính $AO$ (cùng phía với nửa đường tròn $\left( O \right)$). Một cát tuyến bất kỳ qua $A$ cắt $\left( {O'} \right);\left( O \right)$ lần lượt tại $C,D$. Câu 10
Chọn khẳng định sai?
Câu 11
Nếu $BC$ là tiếp tuyến của nửa đường tròn $\left( {O'} \right)$ thì tính $BC$ theo $R$ (với $OA = R$)
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $MN$ với $M \in \left( O \right)$; $N \in \left( {O'} \right)$. Gọi $P$ là điểm đối xứng với $M$ qua $OO'$; $Q$ là điểm đối xứng với $N$ qua $OO'$. Câu 12
Khi đó, tứ giác $MNQP$ là hình gì?
Câu 13
$MN + PQ$ bằng
Câu 14 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 6\,cm.$
Câu 15 :
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\) tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\) và \(B'.\) Câu 16
Chọn câu đúng nhất.
Câu 17
Tính diện tích tam giác \(A'B'C'.\)
Câu 18 :
Cho hai đường tròn (O;5) và (O’;5) cắt nhau tại A và B. Biết OO’=8. Độ dài dây cung AB là
Câu 19 :
Cho đường tròn tâm \(O\) bán kính \(R = 2cm\) và đường tròn tâm \(O'\) bán kính \(R' = 3cm.\) Biết \(OO' = 6cm.\) Số tiếp tuyến chung của hai đường tròn đã cho là:
Câu 20 :
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là
Đáp án : A Lời giải chi tiết :
Hai đường tròn tiếp xúc với nhau thì có một điểm chung duy nhất
Câu 2 :
Cho hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$ với $R > r$ cắt nhau tại hai điểm phân biệt và $OO' = d$. Chọn khẳng định đúng?
Đáp án : C Lời giải chi tiết :
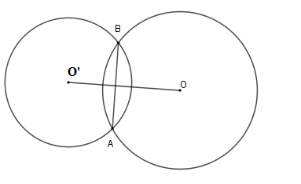 Hai đường tròn $\left( {O;R} \right)$ và $\left( {O';r} \right)$$\left( {R > r} \right)$cắt nhau. Khi đó $\left( O \right)$ và $\left( {O'} \right)$ có hai điểm chung và đường nối tâm là đường trung trực của đoạn $AB$. Hệ thức liên hệ $R - r < OO' < R + r$
Câu 3 :
Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là
Đáp án : D Phương pháp giải :
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
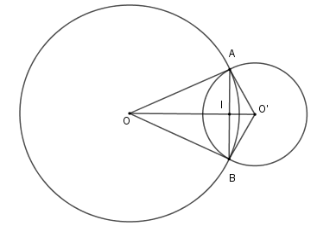 Vì $OA$ là tiếp tuyến của $\left( {O'} \right)$ nên $\Delta OAO'$ vuông tại $A$. Vì $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A,B$ nên đường nối tâm $OO'$ là trung trực của đoạn $AB$. Gọi giao điểm của $AB$ và $OO'$ là $I$ thì $AB \bot OO'$ tại $I$ là trung điểm của $AB$ Áp dụng hệ thức lượng trong tam giác vuông $OAO'$ ta có $\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{8^2}}} + \dfrac{1}{{{6^2}}} \Rightarrow AI = 4,8\,cm \Rightarrow AB = 9,6\,cm$
Câu 4 :
Cho hai đường tròn \(\left( {I;7cm} \right)\) và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là:
Đáp án : A Phương pháp giải :
Xét hai đường tròn \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) ta có: +) \(\left| {{R_1} - {R_2}} \right| < {O_1}{O_2} < {R_1} + {R_2}\) thì \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) cắt nhau. +) \({O_1}{O_2} > {R_1} + {R_2}\) thì \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) ngoài nhau. +) \({O_1}{O_2} < \left| {{R_1} - {R_2}} \right|\) thì \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) trong nhau. +) \({O_1}{O_2} = {R_1} + {R_2}\) thì \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) tiếp xúc ngoài. +) \({O_1}{O_2} = \left| {{R_1} - {R_2}} \right|\) thì \(\left( {{O_1};\;{R_1}} \right)\) và \(\left( {{O_2};\;{R_2}} \right)\) tiếp xúc trong. Lời giải chi tiết :
Ta có: \({R_1} + {R_2} = 7 + 5 = 12;\;\;\left| {{R_1} - {R_2}} \right| = 7 - 5 = 2 = IK.\;\;\) \( \Rightarrow \left( {I;\;7cm} \right),\;\left( {K;\;5cm} \right)\) tiếp xúc trong với nhau. Cho đường tròn $\left( O \right)$ bán kính $OA$ và đường tròn $\left( {O'} \right)$ đường kính $OA$. Câu 5
Vị trí tương đối của hai đường tròn là
Đáp án : D Lời giải chi tiết :
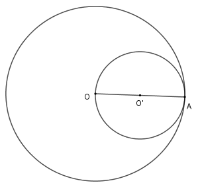 Vì hai đường tròn có một điểm chung là $A$ và $OO' = OA - \dfrac{{OA}}{2} = R - r$ nên hai đường tròn tiếp xúc trong. Câu 6
Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ tại $C$. Khi đó
Đáp án : B Phương pháp giải :
Sử dụng tính chất tam giác cân. Lời giải chi tiết :
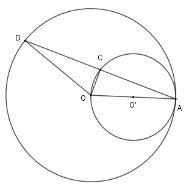 Xét đường tròn $\left( {O'} \right)$ có $OA$ là đường kính và $C \in \left( {O'} \right)$ nên $\Delta ACO$ vuông tại $C$ hay $OC \bot AD$ Xét đường tròn $\left( O \right)$có $OA = OD \Rightarrow \Delta OAD$ cân tại $O$ có $OC$ là đường cao cũng là đường trung tuyến nên $CD = CA$ Cho hai đường tròn $\left( {{O_1}} \right)$ và $\left( {{O_2}} \right)$ tiếp xúc ngoài tại $A$ và một đường thẳng $d$ tiếp xúc với $\left( {{O_1}} \right);\left( {{O_2}} \right)$ lần lượt tại $B,C$. Câu 7
Tam giác $ABC$ là
Đáp án : C Phương pháp giải :
Sử dụng phương pháp cộng góc Lời giải chi tiết :
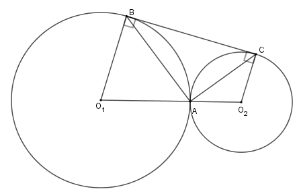 Xét $\left( {{O_1}} \right)$ có ${O_1}B = {O_1}A$ $\Rightarrow \Delta {O_1}AB$ cân tại ${O_1}$ $\Rightarrow \widehat {{O_1}BA} = \widehat {{O_1}AB}$ Xét $\left( {{O_2}} \right)$ có ${O_2}C = {O_2}A $ $\Rightarrow \Delta {O_2}CA$ cân tại ${O_2}$ $\Rightarrow \widehat {{O_2}CA} = \widehat {{O_2}AC}$ Mà $\widehat {{O_1}} + \widehat {{O_2}} = 360^\circ - \widehat C - \widehat B = 180^\circ $ $ \Leftrightarrow 180^\circ - \widehat {{O_1}BA} - \widehat {{O_1}AB} + 180^\circ - \widehat {{O_2}CA} - \widehat {{O_2}AC} = 180^\circ $ $\Leftrightarrow 2\left( {\widehat {{O_1}AB} + \widehat {{O_2}AC}} \right) = 180^\circ $ $ \Rightarrow \widehat {{O_1}AB} + \widehat {{O_2}AC} = 90^\circ $ $ \Rightarrow \widehat {BAC} = 90^\circ $ $\Rightarrow \Delta ABC$ vuông tại $A$. Câu 8
Lấy $M$ là trung điểm của $BC$. Chọn khẳng định sai?
Đáp án : B Phương pháp giải :
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của một đường tròn Lời giải chi tiết :
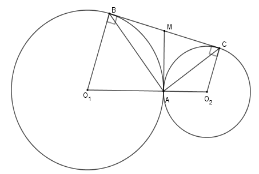 Vì $\Delta ABC$ vuông tại $A$ có $AM$ là trung tuyến nên $AM = BM = DM = \dfrac{{BC}}{2}$ Xét tam giác $BMA$ cân tại $M$ $ \Rightarrow \widehat {MBA} = \widehat {MAB}$, mà $\widehat {{O_1}BA} = \widehat {{O_1}AB}$ (cmt) nên $\widehat {{O_1}BA} + \widehat {MBA} = \widehat {{O_1}AB} + \widehat {MAB} \Rightarrow \widehat {{O_1}AM} = \widehat {{O_1}BM} = 90^\circ $$ \Rightarrow MA \bot A{O_1}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_1}} \right)$ Tương tự ta cũng có $ \Rightarrow MA \bot A{O_2}$ tại $A$ nên $AM$ là tiếp tuyến của $\left( {{O_2}} \right)$ Hay $AM$ là tiếp tuyến chung của hai đường tròn Vậy phương án A, C, D đúng. B sai.
Câu 9 :
Cho hai đường tròn $\left( {O;20cm} \right)$ và $\left( {O';15cm} \right)$ cắt nhau tại $A$ và$B$. Tính đoạn nối tâm $OO'$, biết rằng$AB = 24cm$ và $O$ và $O'$ nằm cùng phía đối với $AB$ .
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và định lý Pytago Lời giải chi tiết :
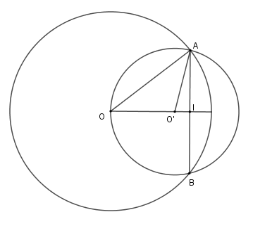 Ta có: $AI = \dfrac{1}{2}AB = 12\,\ cm$ Theo định lý Pytago ta có $O{I^2} = O{A^2}-A{I^2} = 256$ $ \Rightarrow $ $OI = 16 \,\ cm$ và $O'I = \sqrt {O'{A^2} - I{A^2}} = 9 \,\ cm$ Do đó: $OO' = OI-O'I = 16-9 = 7\left( {cm} \right)$ . Cho nửa đường tròn $\left( O \right)$, đường kính $AB$. Vẽ nửa đường tròn tâm $O'$ đường kính $AO$ (cùng phía với nửa đường tròn $\left( O \right)$). Một cát tuyến bất kỳ qua $A$ cắt $\left( {O'} \right);\left( O \right)$ lần lượt tại $C,D$. Câu 10
Chọn khẳng định sai?
Đáp án : D Phương pháp giải :
Sử dụng đường trung bình của tam giác và quan hệ từ vuông góc đến song song Lời giải chi tiết :
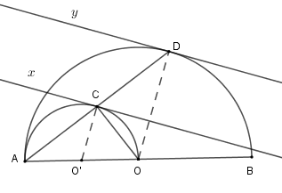 Xét đường tròn $\left( {O'} \right)$ có $AO$ là đường kính và $C \in \left( {O'} \right)$ nên $\widehat {ACO} = 90^\circ \Rightarrow AD \bot CO$ Xét đường tròn $\left( O \right)$ có $OA = OD \Rightarrow \Delta OAD$ cân tại $O$ có $OC$ là đường cao nên $OC$ cũng là đường trung tuyến hay $C$ là trung điểm của $AD$. Xét tam giác $AOD$ có $O'C$ là đường trung bình nên $O'C{\rm{//}}OD$ Kẻ các tiếp tuyến $Cx;Dy$ với các nửa đường tròn ta có $Cx \bot O'C;Dy \bot OD$ mà $O'C{\rm{//}}OD$ nên $Cx{\rm{//}}Dy$ Do đó phương án A, B, C đúng. Câu 11
Nếu $BC$ là tiếp tuyến của nửa đường tròn $\left( {O'} \right)$ thì tính $BC$ theo $R$ (với $OA = R$)
Đáp án : B Phương pháp giải :
Sử dụng định lý Pytago Lời giải chi tiết :
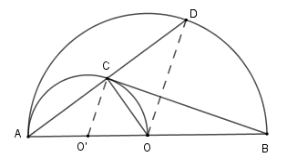 Ta có $OB = R;OO' = \dfrac{R}{2} \Rightarrow O'B = \dfrac{{3R}}{2}$;$O'C = \dfrac{R}{2}$ Theo định lý Pytago ta có $BC = \sqrt {O'{B^2} - O'{C^2}} = \sqrt {\dfrac{{9{R^2}}}{4} - \dfrac{{{R^2}}}{4}} = \sqrt 2 R$ Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $MN$ với $M \in \left( O \right)$; $N \in \left( {O'} \right)$. Gọi $P$ là điểm đối xứng với $M$ qua $OO'$; $Q$ là điểm đối xứng với $N$ qua $OO'$. Câu 12
Khi đó, tứ giác $MNQP$ là hình gì?
Đáp án : A Phương pháp giải :
Sử dụng tính chất tiếp tuyến và dấu hiệu nhận biết các hình đặc biệt Lời giải chi tiết :
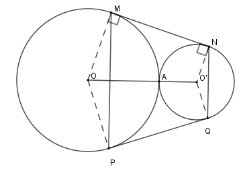 Vì $P$ là điểm đối xứng với $M$ qua $OO'$; $Q$ là điểm đối xứng với $N$ qua $OO'$ nên $MN = PQ$; $P \in \left( O \right);Q \in \left( {O'} \right)$ và $MP \bot OO';NQ \bot OO' $ $\Rightarrow MP{\rm{//}}NQ$ mà $MN = PQ$ nên $MNPQ$ là hình thang cân. Câu 13
$MN + PQ$ bằng
Đáp án : A Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau Lời giải chi tiết :
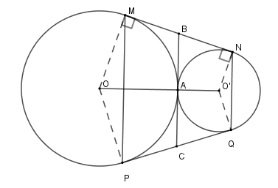 Kẻ tiếp tuyến chung tại $A$ của $\left( O \right);\left( {O'} \right)$ cắt $MN;PQ$ lần lượt tại $B;C$ Ta có $MNPQ$ là hình thang cân nên $\widehat {NMP} = \widehat {QPM}$. Tam giác $OMP$ cân tại $O$ nên $\widehat {OMP} = \widehat {OPM}$ suy ra $\widehat {OMP} + \widehat {PMN} = \widehat {OPM} + \widehat {MPQ} \Rightarrow \widehat {QPO} = 90^\circ $ $ \Rightarrow OP \bot PQ$ tại $P \in \left( O \right)$ nên $PQ$ là tiếp tuyến của $\left( O \right)$. Chứng minh tương tự ta có $PQ$ là tiếp tuyến của $\left( {O'} \right)$ Theo tính chất hai tiếp tuyến cắt nhau ta có $BA = BM = BN;CP = CA = CQ$ suy ra $B;C$ lần lượt là trung điểm của $MN;PQ$ và $MN + PQ = 2MB + 2PC$ $= 2AB + 2AC = 2BC$ Lại có $BC$ là đường trung bình của hình thang $MNQP$ nên $MP + NQ = 2BC$ Do đó $MN + PQ = MP + NQ$.
Câu 14 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 6\,cm.$
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
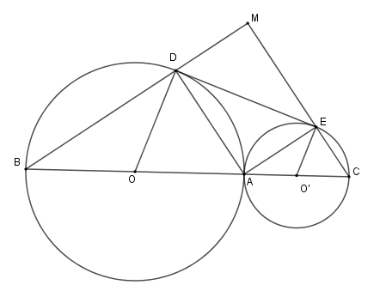 Chứng minh tương tự câu trước ta có được $\widehat {DAE} = 90^\circ $ Mà \(\widehat {BDA} = 90^\circ \) ( vì tam giác \(BAD\) có cạnh \(AB\) là đường kính của \(\left( O \right)\) và \(D \in \left( O \right)\) ) nên \(BD \bot AD \Rightarrow \widehat {MDA} = 90^\circ .\) Tương tự ta có \(\widehat {MEA} = 90^\circ .\) Nên tứ giác $DMEA$ là hình chữ nhật. Xét tam giác $OAD$ cân tại $O$ có $\widehat {DOA} = 60^\circ $ nên $\Delta DOA$ đều, suy ra $OA = AD = 6\,cm$ và $\widehat {ODA} = 60^\circ $ $ \Rightarrow \widehat {ADE} = 30^\circ $. Xét tam giác $ADE$ ta có $EA = AD.\tan \widehat {EDA} = 6.\tan 30^\circ = 2\sqrt 3 $ ${S_{DMEA}} = AD.AE = 6.2\sqrt 3 = 12\sqrt 3 \,\,c{m^2}$.
Câu 15 :
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Đáp án : D Phương pháp giải :
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn Lời giải chi tiết :
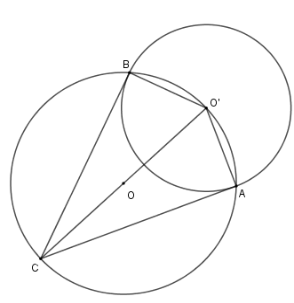 Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$. Do đó $AC,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau) Nên A, B, C đúng. Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\) tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\) và \(B'.\) Câu 16
Chọn câu đúng nhất.
Đáp án : A Phương pháp giải :
+ Sử dụng cách chứng minh tiếp tuyến: Đường thẳng \(d\) là tiếp tuyến của \(\left( O \right)\) tại \(A\) nếu \(d \bot OA\) tại \(A.\) + Sử dụng định lý Pytago để tính \(AA'\) Lời giải chi tiết :
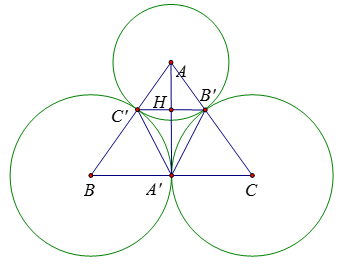 +) Theo tính chất đoạn nối tâm của hai đường tròn tiếp xúc ngoài ta có: \(AB = BC' + C'A = 25\,cm;{\rm{ }}AC = AB' + B'C = 25\,cm;\) \({\rm{ }}BC = BA' + A'C = 30cm\) và \(A'\) là trung điểm của \(BC\) (vì \(A'B = A'C = 15cm\)) \(\Delta ABC\) cân tại \(A\) có \(AA'\) là đường trung tuyến nên cũng là đường cao \( \Rightarrow AA' \bot BC\) \( \Rightarrow AA'\) là tiếp tuyến chung của hai đường tròn (B) và (C) Xét tam giác \(AA'C\) vuông tại \(A'\) có: \(\;A'{A^2}\; = {\rm{ }}A{C^2}\; - {\rm{ }}A'{C^2}\; = {\rm{ }}{25^2} - {\rm{ }}{15^2}\; = 400\)\( \Rightarrow A'A{\rm{ }} = {\rm{ }}20\,cm\) Câu 17
Tính diện tích tam giác \(A'B'C'.\)
Đáp án : B Phương pháp giải :
+ Sử dụng định lý Ta-lét + Sử dụng công thức tính diện tích tam giác bằng nửa tích đường cao và cạnh đáy tương ứng Lời giải chi tiết :
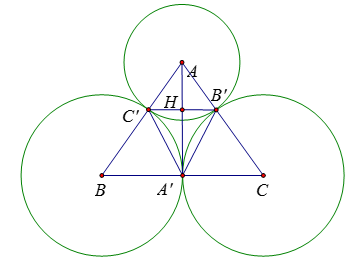 Ta có: \(\dfrac{{AC'}}{{AB}} = \dfrac{{AB'}}{{AC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5}\) \( \Rightarrow B'C'{\rm{ }}//{\rm{ }}BC\) do đó \(B'C' \bot AA'\) Lại có: \(\dfrac{{B'C'}}{{BC}} = \dfrac{{AC'}}{{AB}} \Rightarrow \dfrac{{B'C'}}{{30}} = \dfrac{2}{5} \Leftrightarrow B'C' = 12\,cm\) Xét \(\Delta ABA'\) có \(B'C'{\rm{ }}//{\rm{ }}BC\) nên theo định lý Ta-let ta có \(\dfrac{{AH}}{{A'A}} = \dfrac{{BC'}}{{BA}} \Rightarrow \dfrac{{AH}}{{20}} = \dfrac{{15}}{{25}} \Rightarrow AH = 12\,cm\) (do theo câu trước thì \(AA' = 20\,cm\) ) Diện tích tam giác \(A'B'C'\) là: \(S = \dfrac{1}{2}B'C'.AH = \dfrac{1}{2}.12.12 = 72\,\left( {c{m^2}} \right)\)
Câu 18 :
Cho hai đường tròn (O;5) và (O’;5) cắt nhau tại A và B. Biết OO’=8. Độ dài dây cung AB là
Đáp án : A Phương pháp giải :
Tính chất tam giác cân Định lí Py-ta-go Tính chất hai đường tròn cắt nhau Lời giải chi tiết :
Ta có \(OA=O'A=5cm\) nên tam giác \(AOO'\) cân tại A. Mà AH vuông góc với OO’ nên H là trung điểm của OO’. Suy ra \(OH=4cm\) . Xét tam giác AOH vuông tại H nên suy ra \(A{{H}^{2}}=O{{A}^{2}}-O{{H}^{2}}={{5}^{2}}-{{4}^{2}}=9={{3}^{2}}\). Vậy \(AH=3cm\) . Mà \(AB=2AH\) ( mối quan hệ giữa đường nối tâm và dây cung). Vậy \(AB=6cm\)
Câu 19 :
Cho đường tròn tâm \(O\) bán kính \(R = 2cm\) và đường tròn tâm \(O'\) bán kính \(R' = 3cm.\) Biết \(OO' = 6cm.\) Số tiếp tuyến chung của hai đường tròn đã cho là:
Đáp án : D Phương pháp giải :
Cho hai đường tròn \(\left( {O;\,\,R} \right)\) và \(\left( {O';\,\,R'} \right)\) khi đó ta có: +) \(OO' > R + R'\) thì hai đường tròn nằm ngoài nhau hay hai đường tròn không có điểm chung. \( \Rightarrow \) Hai đường tròn có \(4\) tiếp tuyến chung. +) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn đựng nhau hay hai đường tròn không có điểm chung. \( \Rightarrow \) Hai đường tròn không có tiếp tuyến chung. +) \(\left| {R - R'} \right| < OO' < R + R'\) thì hai đường tròn cắt nhau hay hai đường tròn có hai điểm chung. \( \Rightarrow \) Hai đường tròn có \(2\) tiếp tuyến chung. +) \(OO' = R + R'\) thì hai đường tròn tiếp xúc ngoài hay hai đường tròn có một điểm chung. \( \Rightarrow \) Hai đường tròn có \(1\) tiếp tuyến chung. +) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn tiếp xúc trong hay hai đường tròn có một điểm chung. \( \Rightarrow \) Hai đường tròn có \(1\) tiếp tuyến chung. Lời giải chi tiết :
Ta có: \(OO' = 6cm\) Lại có: \(\left\{ \begin{array}{l}R' = 3cm\\R = 2cm\end{array} \right. \Rightarrow R' + R = 3 + 2 = 5cm < OO'\) \( \Rightarrow \) Hai đường tròn nằm ngoài nhau \( \Rightarrow \) Hai đường tròn có \(4\) tiếp tuyến chung.
Câu 20 :
Cho đường thẳng xy và đường tròn (O; R) không giao nhau. Gọi M là một điểm di động trên xy. Vẽ đường tròn đường kính OM cắt đường tròn (O) tại A và B. Kẻ \(OH \bot xy\) . Chọn câu đúng.
Đáp án : C Phương pháp giải :
+ Sử dụng tam giác đồng dạng + Sử dụng hệ thức lượng trong tam giác vuông để chỉ ra các điểm và đoạn thẳng cố định. Lời giải chi tiết :
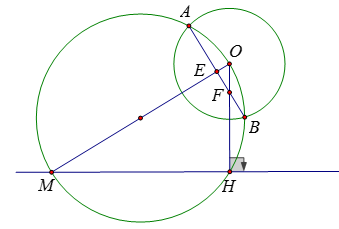 Vì \(OH \bot xy,\) nên \(H\) là một điểm cố định và \(OH\) không đổi Gọi giao điểm của \(AB\) và \(OM\) là \(E;\) giao điểm của \(AB\) với \(OH\) là \(F.\) Vì \(\left( {O;R} \right)\) và đường tròn đường kính \(OM\) cắt nhau tại \(A;B\) nên \(AB \bot OM\) Lại có điểm A nằm trên đường tròn đường kính OM nên \(\widehat {OAM} = 90^\circ \) Xét \(\Delta OEF\) và \(\Delta OHM\) có \(\widehat O\) chung và \(\widehat {OEF} = \widehat {OHM} = 90^\circ \) nên \(\Delta OEF \backsim \Delta OHM\left( {g - g} \right)\) Suy ra \(\dfrac{{OE}}{{OH}} = \dfrac{{OF}}{{OM}} \Rightarrow OE.OM = OF.OH\) Xét \(\Delta MAO\) vuông tại \(A\) có \(AE\) là đường cao nên theo hệ thức lượng trong tam giác vuông ta có \(\begin{array}{*{20}{l}}{OM.OE = O{A^2}\; = {R^2}}\\{\; \Rightarrow OF.OH = {R^2}\; \Rightarrow OF = \dfrac{{{R^2}}}{{OH}}}\end{array}\) Do \(OH\) không đổi nên \(OF\) cũng không đổi Vậy \(F\) là một điểm cố định hay \(AB\) luôn đi qua một điểm cố định là giao của \(AB\) và \(OH.\)
|



















Danh sách bình luận