Trắc nghiệm Bài 2: Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích hình nón Toán 9Đề bài
Câu 1 :
Cho hình nón có bán kính đáy \(R = 3\,\left( {cm} \right)\) và chiều cao \(h = 4\,\left( {cm} \right)\) . Diện tích xung quanh của hình nón là
Câu 2 :
Cho hình nón có đường kính đáy \(d = 10\,cm\) và diện tích xung quanh \(65\pi \,\left( {c{m^2}} \right)\). Tính thể tích khối nón.
Câu 3 :
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
Câu 4 :
Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là $10\,cm$ và $5cm$, chiều cao là $20cm$ . Tính dung tích của xô.
Câu 5 :
Cho tam giác vuông \(ABC\) vuông tại \(A\) có \(BC = 20\,cm;AC = 12\,cm\) . Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là :
Câu 6 :
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
Câu 7 :
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
Câu 8 :
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
Câu 9 :
Cho một hình quạt tròn có bán kính \(20\,cm\) và góc ở tâm là ${144^o}$ . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
Từ một khúc gỗ hình trụ cao $15\,cm$, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là $640\pi \,\,c{m^3}$ . 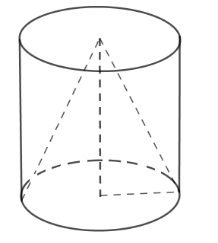 Câu 10
Tính thể tích của khúc gỗ hình trụ.
Câu 11
Tính diện tích xung quanh của hình nón.
Lời giải và đáp án
Câu 1 :
Cho hình nón có bán kính đáy \(R = 3\,\left( {cm} \right)\) và chiều cao \(h = 4\,\left( {cm} \right)\) . Diện tích xung quanh của hình nón là
Đáp án : D Phương pháp giải :
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tính đường sinh Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) Lời giải chi tiết :
Vì \({R^2} + {h^2} = {l^2}\) hay \({3^2} + {4^2} = {l^2}\) nên \({l^2} = 25\) suy ra \(l = 5\,cm\) Diện tích xung quanh của hình trụ là: \({S_{xq}} = \pi Rl = \pi .3.5 = 15\pi \,\,\left( {c{m^2}} \right)\)
Câu 2 :
Cho hình nón có đường kính đáy \(d = 10\,cm\) và diện tích xung quanh \(65\pi \,\left( {c{m^2}} \right)\). Tính thể tích khối nón.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) để tính đường sinh. Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) để tìm chiều cao hình nón Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h.\) Lời giải chi tiết :
Bán kính đường tròn đáy là: \(R = \dfrac{d}{2} = \dfrac{{10}}{2} = 5\,cm\) Diện tích xung quanh là: \({S_{xq}} = \pi Rl = \pi .5.l = 65\pi \) Suy ra \(l = 13\,cm\) Ta có \({R^2} + {h^2} = {l^2}\) \({5^2} + {h^2} = {13^2}\) \({h^2} = 144\) Suy ra \( h = 12\,cm\) Thể tích khối nón là: \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.5^2}.12 \) \(= 100\pi \,\left( {c{m^3}} \right)\)
Câu 3 :
Cho hình nón có chiều cao \(h = 10\,cm\) và thể tích \(V = 1000\pi \,\left( {c{m^3}} \right)\) . Tính diện tích toàn phần của hình nón
Đáp án : B Phương pháp giải :
Sử dụng công thức thể tich khối nón \(V = \dfrac{1}{3}\pi {R^2}h\) để tính bán kính đường tròn đáy Sử dụng công thức liên hệ\({R^2} + {h^2} = {l^2}\) để tìm đường sinh của hình nón Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) Lời giải chi tiết :
Ta có \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {R^2}.10 = 1000\pi \) nên \({R^2} = 300\) suy ra \( R = 10\sqrt 3 \) Và \({R^2} + {h^2} = {l^2}\) hay \( {10^2} + {\left( {10\sqrt 3 } \right)^2} = {l^2} \) suy ra \( l = 20\,cm\) Diện tích toàn phần của hình nón là: \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .10\sqrt3.20 + \pi.300= (300+200\sqrt3)\pi \,\left( {c{m^2}} \right)\)
Câu 4 :
Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là $10\,cm$ và $5cm$, chiều cao là $20cm$ . Tính dung tích của xô.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích khối nón cụt $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}).$ Lời giải chi tiết :
Ta có $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}) = \dfrac{1}{3}\pi .20.\left( {{{10}^2} + 10.5 + {5^2}} \right) = \dfrac{{3500\pi }}{3}\,\,\left( {c{m^3}} \right)$
Câu 5 :
Cho tam giác vuông \(ABC\) vuông tại \(A\) có \(BC = 20\,cm;AC = 12\,cm\) . Quay tam giác \(ABC\) cạnh \(AB\) ta được một hình nón có thể tích là :
Đáp án : D Phương pháp giải :
Sử dụng công thức tính thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$ Lời giải chi tiết :
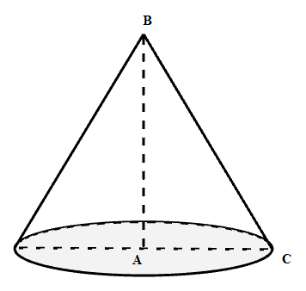 Khi quay tam giác \(ABC\) quanh cạnh \(AB\) ta được một hình nón có chiều cao \(AB\) và bán kính đường tròn đáy là cạnh \(AC\) . Theo định lí Pytagore ta có: \(A{B^2} = B{C^2} - A{C^2} = {20^2} - {12^2} = 256\) suy ra \(AB = 16\) Thể tích của khối nón là: \(V = \dfrac{1}{3}\pi A{C^2}AB = \dfrac{1}{3}\pi {.12^2}.16 = 768\pi \,\,\left( {c{m^3}} \right)\)
Câu 6 :
Cho hình thang vuông $ABDC$ vuông tại $A$ và $B$ , biết cạnh $AB = BC = 3m,AD = 5cm$. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh $AB$ .
Đáp án : B Phương pháp giải :
Tính đáy \(BD\)và \(CD\) theo định lý Pytago Sử dụng công thức diện tích xung quanh hình nón cụt ${S_{xq}} = \pi (R + r)l.$ Lời giải chi tiết :
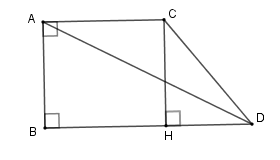 Xét tam giác vuông \(ABD\) ta có \(BD = \sqrt {A{D^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( {cm} \right)\) Kẻ $CH \bot BD$ tại \(H\) . Khi đó \(ACHB\) là hình vuông nên\(CH = AB = AC = BH = 3\,cm \Rightarrow HD = 4 - 3 = 1\,cm\) Xét tam giác vuông \(CHD\) ta có \(C{D^2} = C{H^2} + H{D^2} = {3^2} + {1^2}=10\Rightarrow CD = \sqrt {10} \) Khi quay hình thang vuông \(ABDC\) quanh cạnh \(AB\) ta được hình nón cụt có bán kính đáy nhỏ \(AC\) , bán kính đáy lớn \(BD\) , đường sinh \(CD\) và chiều cao \(AB\) . Khi đó diện tích xung quanh hình nón cụt là ${S_{xq}} = \pi (R + r)l = \pi \left( {3 + 4} \right)\sqrt {10} = 7\pi \sqrt {10} \,\,\left( {c{m^2}} \right)$
Câu 7 :
Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó
Đáp án : A Phương pháp giải :
Sử dụng công thức liên hệ \({R^2} + {h^2} = {l^2}\) Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi Rl\) . Lời giải chi tiết :
Ta có đường sinh mới là: \({l'^2} = {\left( {2R} \right)^2} + {\left( {2h} \right)^2} = 4\left( {{R^2} + {h^2}} \right) = {\left( {2l} \right)^2} \) Suy ra \(l' = 2l\) Khi đó diện tích xung quanh mới là: \({S'_{xq}} = \pi .\left( {2R} \right).\left( {2l} \right) = 4.\pi Rl = 4{S_{xq}}\) . Vậy diện tích xung quanh của hình nón tăng \(4\) lần.
Câu 8 :
Cho tam giác \(ABC\) đều cạnh \(a\) , đường trung tuyến \(AM\) . Quay tam giác \(ABC\) quanh cạnh \(AM\) . Tính diện tích toàn phần của hình nón tạo thành.
Đáp án : B Phương pháp giải :
Sử dụng công thức tính diện tích toàn phần của hình nón \({S_{tp}} = \pi Rl + \pi {R^2}\) . Lời giải chi tiết :
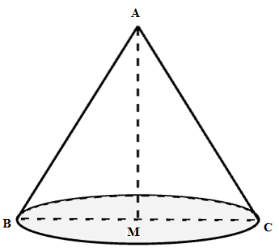 Xét tam giác \(ABC\) đều có \(AM\) vừa là đường trung tuyến, đường cao, đường phân giác. Nên ta có \(MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\) . Khi quay tam giác $ABC$ quanh cạnh \(AM\) ta được hình nón đỉnh \(A\) , bán kính đáy là \(MC\) , đường sinh \(AC\) và chiều cao \(AM\) . Diện tích toàn phần của hình nón là \({S_{tp}} = \pi Rl + \pi {R^2} = \pi .MC.AC + \pi .M{C^2} = \pi .\dfrac{a}{2}.a + \pi .{\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{3\pi {a^2}}}{4}\) .
Câu 9 :
Cho một hình quạt tròn có bán kính \(20\,cm\) và góc ở tâm là ${144^o}$ . Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
Đáp án : D Phương pháp giải :
Sử dụng công thức thể tích khối nón $V = \dfrac{1}{3}\pi {R^2}h$ Lời giải chi tiết :
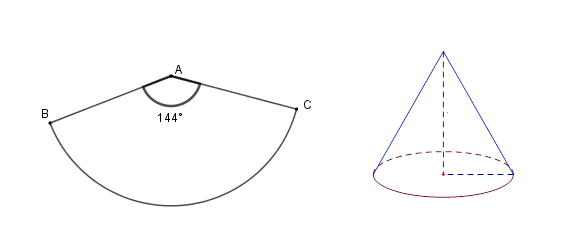 Ta uốn hình quạt \(BAC\) thành hình nón đỉnh \(A\) , đường sinh \(AB = 20\,cm\) . Khi đó độ dài cung \(BC\) chính là chu vi đáy của hình nón Ta có độ dài cung \(BC\) là \({l_{BC}} = \dfrac{{\pi .20.144}}{{180}} = 16\pi \) Khi đó chu vi đáy của hình nón là: \(C = 2\pi R = 16\pi\) suy ra \( R = 8\,cm\) Suy ra \({h^2} = {l^2} - {R^2} = {20^2} - {8^2} \) suy ra \( h = 4\sqrt {21} \,cm\) Thể tích khối nón là: \(V = \dfrac{1}{3}\pi {.8^2}.4\sqrt {21} = \dfrac{{256\pi \sqrt {21} }}{3}\) \(\left( {c{m^3}} \right)\) Từ một khúc gỗ hình trụ cao $15\,cm$, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là $640\pi \,\,c{m^3}$ .  Câu 10
Tính thể tích của khúc gỗ hình trụ.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) và thể tích khối nón \(V = \dfrac{1}{3}{R^2}h\) để suy ra mối quan hệ giữa thể tích hai khối và phần gỗ bỏ đi. Lời giải chi tiết :
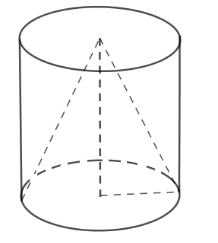 Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên \({V_{trụ}} = \pi {R^2}h\) và \({V_{nón}} = \dfrac{1}{3}\pi {R^2}h\) Suy ra \({V_{trụ}} = 3{V_{nón}}\). Do đó phần gỗ bỏ đi chiếm \(\dfrac{2}{3}\) thể tích khối trụ. Nên thể tích khối trụ là \({V_{trụ}} = 640\pi :\dfrac{2}{3} = 960\pi \,\,\left( {c{m^3}} \right)\) . Câu 11
Tính diện tích xung quanh của hình nón.
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\) để tìm bán kính đáy Sử dụng công thức tính diện tích xung quanh hình nón \(S = \pi Rl\). Lời giải chi tiết :
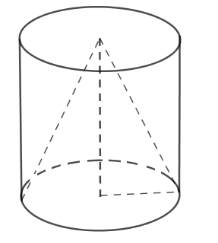 Ta có \({V_{trụ}} = \pi {R^2}h = 960\pi \) \(\pi {R^2}.15 = 960\pi \) Suy ra \( R = 8\,cm\) nên bán kính đáy của hình nón là \(R = 8\,cm\). Chiều cao hình nón \(h = 15\,cm\) suy ra đường sinh hình nón \({l^2} = {h^2} + {R^2} \) suy ra \(l = 17\,cm\) Diện tích xung quanh hình nón là: \(S = \pi Rl = \pi .8.17 = 136\pi \,\left( {c{m^2}} \right)\) .
|



















Danh sách bình luận