Trắc nghiệm Bài tập hay và khó chương đường tròn Toán 9Đề bài
Câu 1 :
Cho đường tròn $\left( {O;R} \right),$ đường kính $AB$ cố định và dây $AC.$ Biết rằng khoảng cách từ $O$ lần lượt đến $AC$ và $BC$ là $8{\rm{ }}cm$ và $6{\rm{ }}cm.$ Lấy $D$ đối xứng với $A$ qua $C.$ Chọn câu sai ?
Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$ Câu 2
Tìm vị trí điểm $M$ để tứ giác $ABDC$ có chu vi nhỏ nhất.
Câu 3
Tìm vị trí điểm $C$ và $D$ để hình thang $ABDC$ có chu vi bằng $14,$ biết $AB = 4{\rm{ }}cm.$
Câu 4 :
Cho nửa đường tròn $\left( O \right)$ có đường kính $AB.$ Vẽ các tiếp tuyến $Ax,{\rm{ }}By$ ($Ax,{\rm{ }}By$ và nửa đường tròn cùng thuộc một nửa mặt phẳng có bờ là $AB$ ). Qua một điểm $M$ thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt $Ax$ và $By$ theo thứ tự ở $C$ và $D.$ Gọi $N = AD \cap BC,{\rm{ }}H = MN \cap AB.$ Chọn câu đúng nhất.
Câu 5 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $BC,B \in \left( O \right)$ và $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ tại $I$. Tính độ dài $BC$ biết $OA = 9cm,O'A = 4cm$.
Câu 6 :
Cho tam giác $ABC$ nội tiếp đường tròn $\left( {O;R} \right)$ có $AB = 5cm,AC = 12cm$ và đường cao $AH = 3cm$ ($H$ nằm ngoài $BC$) , khi đó $R$ bằng
Câu 7 :
Tam giác đều có cạnh 8cm thì bán kính đường tròn nội tiếp tam giác là
Câu 8 :
Hai tiếp tuyến tại A và B của đường tròn (O;R) cắt nhau tại M. Nếu MA=$R\sqrt 3 $ thì góc ở tâm $\widehat {AOB}$ bằng:
Câu 9 :
Cho đường tròn \(\left( {O;R} \right)\), \(AC\) và \(BD\) là hai đường kính . Xác định vị trí của hai đường kính \(AC\) và \(BD\) để diện tích tứ giác \(ABCD\) lớn nhất.
Câu 10 :
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB,CD\) là dây cung của \(\left( O \right)\), \(\widehat {COD} = {90^0}\), \(CD\) cắt \(AB\) tại \(M\) (\(D\) nằm giữa \(C\) và \(M\)) và \(OM = 2R\). Tính độ dài các đoạn thẳng \(MD,MC\) theo \(R\).
Câu 11 :
Cho điểm \(A\) ở ngoài đường tròn \(\left( {O;R} \right)\). Vẽ cát tuyến \(ABC\) và tiếp tuyến \(AM\) với đường tròn \(\left( O \right)\). \(M\) là tiếp điểm. Chọn câu đúng nhất.
Câu 12 :
Cho đường tròn \(\left( {O;r} \right)\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC\) tại \(D\). Vẽ đường kính $DE;$ kéo dài \(AE\) cắt \(BC\) tại \(M\). Chọn câu đúng nhất.
Câu 13 :
Cho tam giác \(ABC\). Một đường tròn tâm \(O\) nội tiếp tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(D\). Đường tròn tâm \(I\) là đường tròn bàng tiếp trong góc \(A\) của tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(F\). Vẽ đường kính \(DE\) của đường tròn \(\left( O \right)\). Chọn đáp án đúng nhất.
Câu 14 :
Đường tròn tâm \(I\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC,AB,AC\) lần lượt ở \(D,E,F\). Đường thẳng qua \(E\) song song với \(BC\) cắt \(AD,DF\) lần lượt ở \(M,N\). Khi đó \(M\) là trung điểm của đoạn thẳng
Câu 15 :
Cho tam giác nhọn \(ABC\). Gọi \(O\) là trung điểm của \(BC\). Dựng đường tròn tâm \(O\) đường kính \(BC\). Vẽ đường cao \(AD\) của tam giác \(ABC\) và các tiếp tuyến \(AM,AN\) với đường tròn \(\left( O \right)\) (\(M,N\) là các tiếp điểm). Gọi \(E\) là giao điểm của \(MN\) với \(AD\). Chọn câu đúng.
Câu 16 :
Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\), \(AH\) là đường cao \(\left( {H \in BC} \right)\). Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Cho đường tròn $\left( {O;R} \right),$ đường kính $AB$ cố định và dây $AC.$ Biết rằng khoảng cách từ $O$ lần lượt đến $AC$ và $BC$ là $8{\rm{ }}cm$ và $6{\rm{ }}cm.$ Lấy $D$ đối xứng với $A$ qua $C.$ Chọn câu sai ?
Đáp án : D Phương pháp giải :
+ Sử dụng : Đường kính vuông góc với dây thì đi qua trung điểm của dây đó. + Chứng minh tam giác \(ABD\) cân từ đó tính \(BD\) suy ra quỹ tích điểm \(D.\) Lời giải chi tiết :
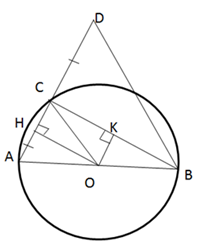 Kẻ $OH,{\rm{ }}OK$ lần lượt vuông góc với $AC$ và $BC,$ ta có : $OH = 8\left( {cm} \right);OK = 6\left( {cm} \right)$ và \(HA = HC = \dfrac{{AC}}{2}\) ; \(KB = KC = \dfrac{{BC}}{2}\) (định lí đường kính dây cung). $AB$ là đường kính nên \(\widehat {ACB} = {90^0}\). Do đó tứ giác $CHOK$ là hình chữ nhật (có ba góc vuông) $ \Rightarrow OH = CK = 8\left( {cm} \right) \Rightarrow BC = 16{\rm{ }}\left( {cm} \right)$ Tương tự có: $AC = 12\left( {cm} \right)$ Xét tam giác vuông $OHC,$ ta có: \(OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {{8^2} + {6^2}} = 10\,\,\left( {cm} \right)\) (định lý Py – ta – go) $\Delta ABD$ có đường cao $BC$ đồng thời là đường trung tuyến nên $\Delta ABD$ cân tại $B.$ Ta có $BD = BA = 2R\left( {cm} \right),$ điểm $B$ cố định, $2R$ không đổi. Vậy $D$ thuộc đường tròn cố định tâm $B$ và bán kính bằng $2R.$ Do đó D sai. Cho nửa đường tròn tâm $O$ đường kính $AB.$ Vẽ các tiếp tuyến $Ax$ và $By$ ($Ax$ và $By$ và nửa đường tròn cùng thuộc về một nửa mặt phẳng bờ là $AB$ ). Gọi $M$ là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại $M$ cắt $Ax$ và $By$ theo thứ tự tại $C$ và $D.$ Câu 2
Tìm vị trí điểm $M$ để tứ giác $ABDC$ có chu vi nhỏ nhất.
Đáp án : C Phương pháp giải :
Chỉ ra $ABDC$ là hình thang Tính chu vi hình thang $ABDC$ rồi lập luận để có chu vi nhỏ nhất là \(CD//AB\) từ đó suy ra vị trí điểm \(M.\) Lời giải chi tiết :
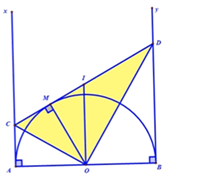 Xét tứ giác $ABDC$ có: $AC//BD \Rightarrow ABDC$ là hình thang Vì hai tiếp tuyến \(CD\) và \(Ax\) cắt nhau tại \(C\), hai tiếp tuyến \(DC\) và \(By\) cắt nhau tại \(D\) nên \(AC = CM;BD = BM\) (tính chất hai tiếp tuyến cắt nhau). Chu vi hình thang $ABDC$ là: ${C_{ABDC}} = AC + AB + BD + CD = CM + AB + DM + CD = AB + 2CD$ $ \Rightarrow {C_{ABDC}}_{\min }\,\,{\rm{khi}}\,\,\,C{D_{\min }} \Rightarrow CD = AB \Rightarrow CD//AB$ Mà $OM\; \bot CD \Rightarrow OM\; \bot AB$ $ \Rightarrow {C_{ABDC\min }} = AB + 2AB = 3AB$ Vậy chu vi nhỏ nhất của hình thang $ABDC$ là $3AB$ khi $OM\; \bot AB.$ Câu 3
Tìm vị trí điểm $C$ và $D$ để hình thang $ABDC$ có chu vi bằng $14,$ biết $AB = 4{\rm{ }}cm.$
Đáp án : A Phương pháp giải :
+ Tính \(CD\) dựa vào chu vi \(ABCD.\) + Tính \(BD\) dựa vào hệ thức lượng, từ đó tính \(AC.\) Lời giải chi tiết :
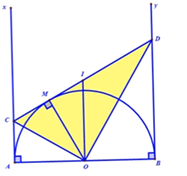 Gọi \(I\) là trung điểm của $CD$ Suy ra $I$ là tâm của đường tròn đường kính $CD$ Theo tính chất hai tiếp tuyến cắt nhau: $AC = CM\;$ và $BD = DM$ Xét tứ giác $ABDC$ có: $AC//BD \Rightarrow ABDC$ là hình thang \( \Rightarrow \,IO\) là đường trung bình của hình thang $ABDC$ \( \Rightarrow IO//AC//BD\) mà $AC\; \bot AB{\rm{ }} \Rightarrow IO\; \bot AB{\rm{ }}\left( 1 \right)$ $IO = \dfrac{{AC + BD}}{2} = \dfrac{{CM + DM}}{2} = \dfrac{{CD}}{2}(2)$ Suy ra tam giác \(COD\) vuông tại \(O.\) ${C_{ABDC}} = 14 \Leftrightarrow AB + 2CD = 14 \Rightarrow CD = \dfrac{{14 - AB}}{2} = \dfrac{{14 - 4}}{2} = 5cm$ Lại có: $CD = CM + DM = AC + BD \Rightarrow AC = CD-BD = 5-BD$ Mà tam giác \(COD\) vuông tại \(O.\) Áp dụng hệ thức lượng vào tam giác vuông $COD$ ta có: $O{M^2} = {\rm{ }}CM.DM \Leftrightarrow {2^2} = AC.BD \Leftrightarrow AC.BD = 4 \Leftrightarrow \left( {5 - BD} \right).BD = 4$ \( \Leftrightarrow 5BD--B{D^2} = 4 \Leftrightarrow B{D^2}--5BD + 4 = 0\) \( \Leftrightarrow B{D^2}-BD-4BD + 4 = 0 \Leftrightarrow BD\left( {BD-1} \right)-4\left( {BD-1} \right) = 0\) \( \Leftrightarrow \left( {BD - 1} \right)\left( {BD - 4} \right) = 4\) $ \Leftrightarrow \left[ \begin{array}{l}BD - 1 = 0\\BD - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}BD = 1 \Rightarrow AC = 4\\BD = 4 \Rightarrow AC = 1\end{array} \right.$ Vậy với $AC = 4cm;BD = 1cm$ hoặc $AC = 1{\rm{ }}cm;BD = 4cm$ thì chu vi của hình thang $ABDC$ bằng $14.$
Câu 4 :
Cho nửa đường tròn $\left( O \right)$ có đường kính $AB.$ Vẽ các tiếp tuyến $Ax,{\rm{ }}By$ ($Ax,{\rm{ }}By$ và nửa đường tròn cùng thuộc một nửa mặt phẳng có bờ là $AB$ ). Qua một điểm $M$ thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt $Ax$ và $By$ theo thứ tự ở $C$ và $D.$ Gọi $N = AD \cap BC,{\rm{ }}H = MN \cap AB.$ Chọn câu đúng nhất.
Đáp án : A Phương pháp giải :
+ Sử dụng tính chất hai tiếp tuyến cắt nhau và định lý Ta-lét Lời giải chi tiết :
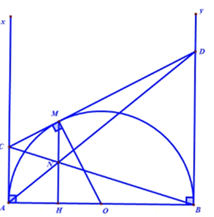 Theo tính chất hai tiếp tuyến cắt nhau ta có: $AC = CM$ và \(BD = DM\) $AC//BD$ (vì cùng vuông góc với$AB$ ) Theo hệ quả của định lý Ta – lét ta có: $\dfrac{{CN}}{{BN}} = \dfrac{{AC}}{{BD}} \Rightarrow \dfrac{{CN}}{{BN}} = \dfrac{{CM}}{{DM}}$ Theo định lý Ta – Lét đảo ta được $MN//BD.$ Mà $BD\; \bot AB \Rightarrow {\rm{ }}MN \bot \;AB$ nên A đúng Theo hệ quả của định lý Ta – Lét ta có: $\dfrac{{NH}}{{BD}} = \dfrac{{AH}}{{AB}} = \dfrac{{CN}}{{CB}} = \dfrac{{MN}}{{BD}} \Rightarrow MN = NH$ nên B sai.
Câu 5 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $BC,B \in \left( O \right)$ và $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ tại $I$. Tính độ dài $BC$ biết $OA = 9cm,O'A = 4cm$.
Đáp án : A Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau Sử dụng công thức lượng giác Lời giải chi tiết :
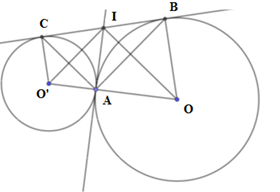 Ta có $IO$ là tia phân giác của \(\widehat {BIA}\) $IO'$ là tia phân giác của \(\widehat {CIA}\) Mà \(\widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}\) Tam giác \(OIO'\) vuông tại \(I\) có \(IA\) là đường cao nên $I{A^2} = AO.AO' = 9.4 = 36 \Rightarrow IA = 6cm$. \( \Rightarrow IA = IB = IC = 6cm\) (tính chất hai tiếp tuyến cắt nhau) Vậy $BC = 2IA = 2.6 = 12\left( {cm} \right)$.
Câu 6 :
Cho tam giác $ABC$ nội tiếp đường tròn $\left( {O;R} \right)$ có $AB = 5cm,AC = 12cm$ và đường cao $AH = 3cm$ ($H$ nằm ngoài $BC$) , khi đó $R$ bằng
Đáp án : D Phương pháp giải :
Dựa vào tính chất tứ giác nội tiếp Định lí pi-ta-go Dấu hiệu và tính chất hai tam giác đồng dạng Lời giải chi tiết :
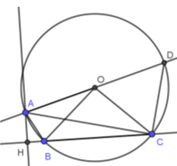 Vẽ đường kính $AD$. Xét \(\Delta AHB\) vuông tại $H$ ta có $A{B^2} = A{H^2} + H{B^2}$ (Py-ta-go) Mà $AB = 5cm,AH = 3cm$ nên $HB = 4cm$. Ta có tứ giác $ABCD$ là tứ giác nội tiếp nên \(\widehat {ADC} + \widehat {ABC} = {180^0}\) (tính chất) Lại có \(\widehat {ABC} + \widehat {ABH} = {180^0}\) (kề bù) nên \(\widehat {ADC} = \widehat {ABH}\). Xét $\Delta AHB$ và \(\Delta DCA\) có: \(\widehat {AHB} = \widehat {ACD} = {90^0}\) \(\widehat {ADC} = \widehat {ABH}\) (cmt) \( \Rightarrow \Delta AHB \backsim \Delta DCA\left( {g.g} \right)\) \( \Rightarrow \dfrac{{HB}}{{CA}} = \dfrac{{AB}}{{DA}} \Rightarrow DA = \dfrac{{CA.AB}}{{HB}} = \dfrac{{12.5}}{4} = 15 \Rightarrow OA = \dfrac{{15}}{2} = 7,5cm\)
Câu 7 :
Tam giác đều có cạnh 8cm thì bán kính đường tròn nội tiếp tam giác là
Đáp án : D Phương pháp giải :
Tính chất tam giác đều Tính chất trung tuyến của tam giác Lời giải chi tiết :
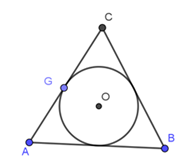 Gọi O là tâm đường tròn nội tiếp tam giác đều ABC. Vậy O là giao điểm 3 đường phân giác của tam giác mà tam giác ABC đều nên O là giao điểm 3 đường trung tuyến của tam giác ABC. Vậy bán kính đường tròn (O) là OG với BG là trung tuyến của tam giác ABC. Vì tam giác ABC đều nên ta tính được: $BG = \sqrt {B{C^2} - C{G^2}} = \sqrt {{8^2} - {4^2}} = 4\sqrt 3 \,cm$$ \Rightarrow OG = \dfrac{{BG}}{3} = \dfrac{{4\sqrt 3 }}{3}\,cm$
Câu 8 :
Hai tiếp tuyến tại A và B của đường tròn (O;R) cắt nhau tại M. Nếu MA=$R\sqrt 3 $ thì góc ở tâm $\widehat {AOB}$ bằng:
Đáp án : A Phương pháp giải :
Tính chất tiếp tuyến của đường tròn Tính chất hai tiếp tuyến cắt nhau Lời giải chi tiết :
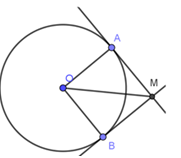 Có $AM$ là tiếp tuyến của đường tròn $\left( O \right)$ nên $AM$ vuông góc với $OA$ Xét tam giác $AOM$ vuông tại $A$ nên có $\tan \widehat {AOM} = \dfrac{{AM}}{{OA}} = \dfrac{{R\sqrt 3 }}{R} = \sqrt 3 $$ \Rightarrow \widehat {AOM} = {60^0}$ Mà hai tiếp tuyến $AM$ và $BM$ cắt nhau tại $M$ nên ta có $OM$ là phân giác của $\widehat {AOB}$ Vậy $\widehat {AOB}$$ = 2\widehat {AOM} = {2.60^0} = {120^0}$
Câu 9 :
Cho đường tròn \(\left( {O;R} \right)\), \(AC\) và \(BD\) là hai đường kính . Xác định vị trí của hai đường kính \(AC\) và \(BD\) để diện tích tứ giác \(ABCD\) lớn nhất.
Đáp án : A Phương pháp giải :
+ Vẽ \(AH \bot BD\left( {H \in BD} \right)\) + Chứng minh \(ABCD\) là hình chữ nhật + Đánh giá \({S_{ABCD}}\) thông qua \({S_{ABD}} = \dfrac{1}{2}AB.AD = \dfrac{1}{2}AH.BD\) Lời giải chi tiết :
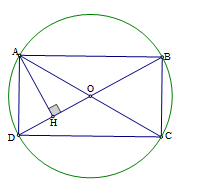 Vẽ \(AH \bot BD\left( {H \in BD} \right)\). Tứ giác \(ABCD\) có \(OA = OA = R,OB = OD = R\) nên là hình bình hành. Mà \(AC = BD = 2R\) do đó tứ giác \(ABCD\) là hình chữ nhật, suy ra \({S_{ABCD}} = AB.AD\) \(\Delta ABD\) có \(\widehat A = {90^0}\), \(AH \bot DB\) nên \(AB.AD = AH.DB\). Vì \(AH \le AO,DB = 2R\) nên \({S_{ABCD}} \le 2{R^2}\) (không đổi). Dấu “=” xảy ra \( \Leftrightarrow H \equiv O \Leftrightarrow AC \bot BD\). Vậy khi hai đường kính \(AC\) và \(BD\) vuông góc với nhau thì diện tích tứ giác \(ABCD\) lớn nhất.
Câu 10 :
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB,CD\) là dây cung của \(\left( O \right)\), \(\widehat {COD} = {90^0}\), \(CD\) cắt \(AB\) tại \(M\) (\(D\) nằm giữa \(C\) và \(M\)) và \(OM = 2R\). Tính độ dài các đoạn thẳng \(MD,MC\) theo \(R\).
Đáp án : D Phương pháp giải :
Gọi \(H\) là trung điểm của \(CD\) Dựa vào định lý Pytago để tính toán Lời giải chi tiết :
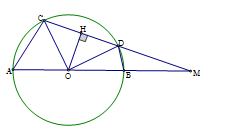 Vì \(\widehat {COD} = {90^0}\) suy ra tam giác \(COD\) vuông cân tại \(O\) nên \(CD = R\sqrt 2 \). Gọi \(H\) là trung điểm của \(CD\) suy ra \(OH \bot CD\) (định lý) Vì \(\Delta HOM\) vuông tại \(H\), \(OH = \dfrac{1}{2}CD = \dfrac{{\sqrt 2 }}{2}R,OM = 2R\). Trong tam giác vuông \(OMH\) ta có: \(M{H^2} = O{M^2} - O{H^2} = 4{R^2} - \dfrac{{{R^2}}}{2} = \dfrac{{7{R^2}}}{2} \Rightarrow MH = \dfrac{{\sqrt {14} }}{2}R\) suy ra \(MD = MH - AH = \dfrac{{R\sqrt 2 }}{2}\left( {\sqrt 7 - 1} \right)\), \(MC = \dfrac{{R\sqrt 2 }}{2}\left( {\sqrt 7 + 1} \right)\)
Câu 11 :
Cho điểm \(A\) ở ngoài đường tròn \(\left( {O;R} \right)\). Vẽ cát tuyến \(ABC\) và tiếp tuyến \(AM\) với đường tròn \(\left( O \right)\). \(M\) là tiếp điểm. Chọn câu đúng nhất.
Đáp án : B Phương pháp giải :
+ Sử dụng định lý đường kính vuông góc dây cung + Sử dụng định lý Pytago và mối quan hệ giữa đường cao và đường xiên để đánh giá. Lời giải chi tiết :
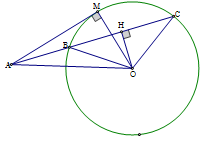 Vẽ \(OH \bot BC,H \in BC\), suy ra \(BH = HC\) (định lý đường kính vuông góc dây cung). Ta có \(AB + AC = \)\(\left( {AH - BH} \right) + \left( {AH + HC} \right) = 2AH\). \(\Delta MAO\) có \(\widehat {AMO} = {90^0}\) Theo định lý Pitago có \(A{M^2} + O{M^2} = O{A^2}\); \(\Delta HAO\) có \(\widehat {AHO} = {90^0}\) nên \(A{H^2} + O{H^2} = O{A^2}\) Mà \(OB = OM = R\), \(OH \le OB\) nên \(OH \le OM\). Do đó $O{H^2} \le O{M^2}$, suy ra \(AH \ge AM\). Từ đó ta có: $AB + AC \ge 2AM$.
Câu 12 :
Cho đường tròn \(\left( {O;r} \right)\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC\) tại \(D\). Vẽ đường kính $DE;$ kéo dài \(AE\) cắt \(BC\) tại \(M\). Chọn câu đúng nhất.
Đáp án : C Phương pháp giải :
Vẽ tiếp tuyến tại \(E\) của đường tròn \(\left( O \right)\) cắt \(AB,AC\) lần lượt tại \(H,K\). Sử dụng tam giác đồng dạng và tính chất dãy tỉ số bằng nhau để so sánh. Lời giải chi tiết :
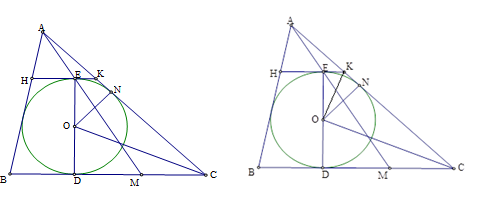 Vẽ tiếp tuyến tại \(E\) của đường tròn \(\left( O \right)\) cắt \(AB,AC\) lần lượt tại \(H,K\).Ta có \(ED \bot HK,ED \bot BC \Rightarrow HK//BC\). Gọi \(N\) là tiếp điểm của đường tròn \(\left( O \right)\) tiếp xúc với \(AC\). \(OK,OC\) là hai tia phân giác của hai góc kề bù \(EON\) và \(NOD\) (tính chất trung tuyến)\( \Rightarrow \widehat {KOC} = {90^0}\). + Xét \(\Delta OEK\) và \(\Delta CDO\) có \(\widehat {OEC} = \widehat {CDO}\left( { = {{90}^0}} \right),\widehat {OKE} = \widehat {COD}\) (cùng phụ với \(\widehat {EOK}\)).Do đó \(\Delta OEK \backsim \Delta CDO \Rightarrow \dfrac{{EK}}{{OD}} = \dfrac{{OE}}{{CD}}\) hay \(\dfrac{{EK}}{r} = \dfrac{r}{{CD}}\). Tương tự cũng có \(\dfrac{{HE}}{r} = \dfrac{r}{{BD}}\). Do vậy \(\dfrac{{EK}}{{HE}} = \dfrac{{BD}}{{CD}} \Rightarrow \dfrac{{EK}}{{EK + HE}} = \dfrac{{BD}}{{BD + CD}}\) hay \(\dfrac{{EK}}{{HK}} = \dfrac{{BD}}{{BC}}\) (1) + Trong \(\Delta ABM\) có \(HE//BM\), áp dụng hệ quả của định lý Thales trong tam giác ta có \(\dfrac{{HE}}{{BM}} = \dfrac{{AE}}{{AM}}\). Tương tự có \(\dfrac{{EK}}{{CM}} = \dfrac{{AE}}{{AM}}\). Do đó \(\dfrac{{HE}}{{BM}} = \dfrac{{EK}}{{CM}} \Rightarrow \dfrac{{EK}}{{CM}} = \dfrac{{EK + HE}}{{CM + BM}}\) hay \(\dfrac{{EK}}{{CM}} = \dfrac{{HK}}{{BC}} \Rightarrow \dfrac{{EK}}{{HK}} = \dfrac{{CM}}{{BC}}\) Từ (1) và (2) cho ta \(BD = CM\).
Câu 13 :
Cho tam giác \(ABC\). Một đường tròn tâm \(O\) nội tiếp tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(D\). Đường tròn tâm \(I\) là đường tròn bàng tiếp trong góc \(A\) của tam giác \(ABC\) và tiếp xúc với \(BC\) tại \(F\). Vẽ đường kính \(DE\) của đường tròn \(\left( O \right)\). Chọn đáp án đúng nhất.
Đáp án : D Phương pháp giải :
Sử dụng hệ quả của định lý Ta-lét, tính chất hai đường thẳng song song và hai tam giác đồng dạng. Chú ý rằng tâm đường tròn bàng tiếp tam giác là giao hai đường phân giác góc ngoài và \(1\) đường phân giác góc trong của tam giác. Lời giải chi tiết :
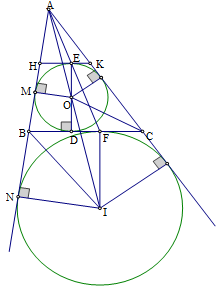 Theo đề ra có \(A,O,I\) thẳng hàng (vì \(O,I\) cùng nằm trên tia phân góc \(A\)). + Gọi \(M,N\) là tiếp điểm của \(\left( O \right)\); \(\left( I \right)\) với \(AB\), ta có \(OM//IN\) nên \(\dfrac{{AO}}{{AI}} = \dfrac{{OM}}{{IN}}\) (hệ quả của định lý Thales). Mà \(OM = OE,IN = IF\) nên có \(\dfrac{{AO}}{{AI}} = \dfrac{{OE}}{{IF}}\). Mặt khác \(ED \bot BC,IF \bot BC\)\( \Rightarrow OD//IF \Rightarrow \widehat {AOE} = \widehat {AIF}\). + Xét \(\Delta OAE\) và \(\Delta IAF\) có \(\dfrac{{AO}}{{AI}} = \dfrac{{OE}}{{IF}};\widehat {AOE} = \widehat {AIF}\), do đó \(\Delta OAE \backsim \Delta IAF \Rightarrow \widehat {OAE} = \widehat {IAF}\). Vậy \(A,E,F\) thẳng hàng.
Câu 14 :
Đường tròn tâm \(I\) nội tiếp tam giác \(ABC\) tiếp xúc với \(BC,AB,AC\) lần lượt ở \(D,E,F\). Đường thẳng qua \(E\) song song với \(BC\) cắt \(AD,DF\) lần lượt ở \(M,N\). Khi đó \(M\) là trung điểm của đoạn thẳng
Đáp án : A Phương pháp giải :
+ Dựng \(AK//BD\left( {K \in DF} \right)\) + Sử dụng tính chất hai tiếp tuyến cắt nhau và định lý Ta-lét để chỉ ra vị trí điểm \(M.\) Lời giải chi tiết :
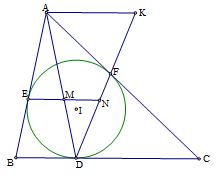 + Vì đường tròn \((I)\) tiếp xúc với các cạnh tại \(D,E,F\) nên suy ra \(AE = AF,BE = BD,CD = CF\). + Dựng \(AK//BD\left( {K \in DF} \right)\) ta có: \(\dfrac{{MN}}{{AK}} = \dfrac{{MD}}{{DA}}\), \(\dfrac{{EM}}{{BD}} = \dfrac{{AM}}{{AD}}\). Ta cần chứng minh: \(\dfrac{{MD}}{{DA}}.AK = \dfrac{{AM}}{{AD}}.BD \Leftrightarrow \dfrac{{MD}}{{AM}} = \dfrac{{BD}}{{AK}}\). Nhưng \(AK = AF = AE\), \(BD = BE\) nên ta cần chứng minh: \(\dfrac{{MD}}{{AM}} = \dfrac{{BE}}{{AE}}\) (điều này là hiển nhiên theo định lý Ta-let).
Câu 15 :
Cho tam giác nhọn \(ABC\). Gọi \(O\) là trung điểm của \(BC\). Dựng đường tròn tâm \(O\) đường kính \(BC\). Vẽ đường cao \(AD\) của tam giác \(ABC\) và các tiếp tuyến \(AM,AN\) với đường tròn \(\left( O \right)\) (\(M,N\) là các tiếp điểm). Gọi \(E\) là giao điểm của \(MN\) với \(AD\). Chọn câu đúng.
Đáp án : B Phương pháp giải :
+ Sử dụng tính chất hai tiếp tuyến cắt nhau để chỉ ra \(AO \bot MN.\) + Gọi \(H\) là giao điểm của \(AO\) và \(MN\). + Sử dụng tính chất hai tam giác đồng dạng và hệ thức lượng trong tam giác vuông để tìm hệ thức đúng. Lời giải chi tiết :
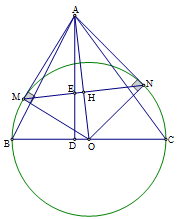 \(AM,AN\) là các tiếp tuyến của đường tròn \(\left( O \right)\), gọi \(H\) là giao điểm của \(AO\) và \(MN\). Theo tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN;\,OM = ON\) nên \(AO\) là đường trung trực của đoạn \(MN.\) Suy ra \(AO \bot MN.\) Ta có tam giác \(AHE\) đồng dạng với tam giác \(ADO\) (vì \(\widehat {AHE} = \widehat {ADO} = 90^\circ ;\widehat {DAO}\) chung) nên \(AE.AD = AH.AO\). (1) Cũng theo hệ thức lượng trong tam giác vuông \(AMO\) ta có: \(AH.AO = A{M^2}\). (2) Từ (1) và (2) suy ra \(AE.AD = A{M^2}.\)
Câu 16 :
Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\), \(AH\) là đường cao \(\left( {H \in BC} \right)\). Chọn câu đúng.
Đáp án : C Phương pháp giải :
Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\) Sử dụng tính chất hai tam giác đồng dạng để tìm hệ thức đúng. Lời giải chi tiết :
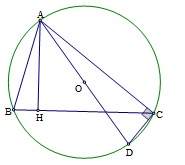 Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\), suy ra \(\widehat {ACD} = {90^0}\) (vì tam giác \(ACD\) có ba đỉnh thuộc đường tròn và \(AD\) là đường kính) Xét \(\Delta HBA\) và \(\Delta CDA\) có: \(\widehat {AHB} = \widehat {ACD}\left( { = {{90}^0}} \right);\widehat {HBA} = \widehat {CDA}\) (góc nội tiếp cùng chắn ), Do đó \(\Delta HBA \backsim \Delta CDA \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{AD}} \Rightarrow AB.AC = AD.AH\). Mà \(AD = 2R\). Do đó \(AB.AC = 2R.AH\).
|



















Danh sách bình luận