Trắc nghiệm Bài 3: Đồ thị hàm số y=ax+b Toán 9Đề bài
Câu 1 :
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
Câu 2 :
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$ 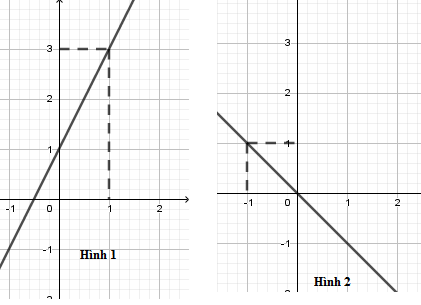 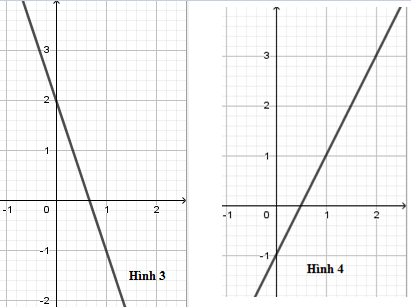
Câu 3 :
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
Câu 4 :
Cho hai đường thẳng ${d_1}:y = 2x - 2$ và ${d_2}:y = 3 - 4x$. Tung độ giao điểm của ${d_1};{d_2}$ có tọa độ là
Câu 5 :
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
Câu 6 :
Cho hàm số $y = \left( {1 - m} \right)x + m$ . Xác định $m$ để đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$
Câu 7 :
Cho hàm số $y = \left( {3 - 2m} \right)x + m - 2$ . Xác định $m$ để đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$.
Câu 8 :
Cho hàm số $y = mx - 2$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = \dfrac{1}{2}x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$.
Câu 9 :
Cho hàm số $y = \left( {m + 1} \right)x - 1$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = 4$.
Câu 10 :
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
Câu 11 :
Cho ba đường thẳng\({d_1}:y = - 2x;{d_2}:y = - 3x - 1;\) \({d_3}:y = x + 3.\) Khẳng định nào dưới đây là đúng?
Câu 12 :
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = x;{d_2}:y = 4 - 3x\) và \({d_3}:y = mx - 3\) đồng quy?
Câu 13 :
Cho đường thẳng \(d:y = - 2x - 4\) . Gọi $A,B$ lần lượt là giao điểm của $d$ với trục hoành và trục tung. Tính diện tích tam giác $OAB.$
Câu 14 :
Cho đường thẳng \({d_1}:y = - x + 2\) và ${d_2}:y = 5 - 4x$. Gọi $A,B$ lần lượt là giao điểm của ${d_1}$ với ${d_2}$ và ${d_1}$ với trục hoành. Tổng hoành độ giao điểm của $A$ và $B$ là
Câu 15 :
Gọi \({d_1}\) là đồ thị hàm số \(y = mx + 1\) và \({d_2}\) là đồ thị hàm số \(y = \dfrac{1}{2}x - 2.\) Xác định giá trị của $m$ để $M\left( {2; - 1} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.
Câu 16 :
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = \left( {m + 2} \right)x - 3;\) \({d_2}:y = 3x + 1\) và \({d_3}:y = 2x - 5\) giao nhau tại một điểm?
Câu 17 :
Hình vẽ bên là đồ thị của hàm số nào dưới đây? 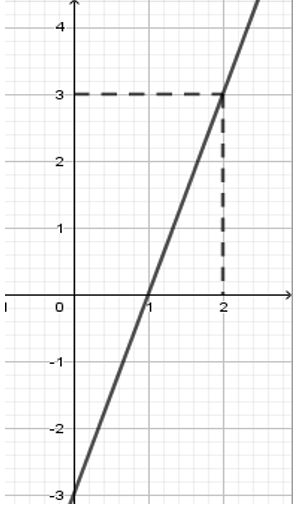
Lời giải và đáp án
Câu 1 :
Chọn khẳng định đúng về đồ thị hàm số \(y = ax + b(a \ne 0).\)
Đáp án : C Lời giải chi tiết :
Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng Trường hợp 1: Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\) Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
Câu 2 :
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$  
Đáp án : D Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\) Lời giải chi tiết :
Đồ thị hàm số $y = 2x + 1$ là đường thẳng đi qua hai điểm có tọa độ $\left( {0;1} \right)$ và $\left( {1;3} \right)$ nên hình 1 là đồ thị hàm số $y = 2x + 1$.
Câu 3 :
Đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ đi qua điểm nào dưới đây?
Đáp án : C Phương pháp giải :
Đồ thị hàm số \(y = ax + b(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\) Lời giải chi tiết :
Thay tọa độ từng điểm vào hàm số ta được +) Với $A\left( {\dfrac{{ - 5}}{3};0} \right)$. Thay $x = - \dfrac{5}{3};y = 0$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { - \dfrac{5}{3} - 1} \right) + \dfrac{4}{3} = 0 \Leftrightarrow \dfrac{{ - 20}}{3} = 0$ (Vô lý) +) Với $B\left( {1;\dfrac{3}{4}} \right)$. Thay $x = 1;y = \dfrac{3}{4}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {1 - 1} \right) + \dfrac{4}{3} = \dfrac{3}{4} \Leftrightarrow \dfrac{4}{3} = \dfrac{3}{4}$ (Vô lý) +) Với $D\left( {4;\dfrac{4}{3}} \right)$. Thay $x = 4;y = \dfrac{4}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( {4 - 1} \right) + \dfrac{4}{3} = \dfrac{4}{3} \Leftrightarrow \dfrac{{31}}{3} = \dfrac{4}{3}$ (Vô lý) +)Với $C\left( { \dfrac{2}{3};\dfrac{1}{3}} \right)$. Thay $x = \dfrac{2}{3};y = \dfrac{1}{3}$ vào $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$ ta được $3\left( { \dfrac{2}{3} - 1} \right) + \dfrac{4}{3} = \dfrac{1}{3} \Leftrightarrow \dfrac{1}{3} = \dfrac{1}{3}$ (luôn đúng) $ \Rightarrow C$ thuộc đồ thị hàm số $y = 3\left( {x - 1} \right) + \dfrac{4}{3}$
Câu 4 :
Cho hai đường thẳng ${d_1}:y = 2x - 2$ và ${d_2}:y = 3 - 4x$. Tung độ giao điểm của ${d_1};{d_2}$ có tọa độ là
Đáp án : A Phương pháp giải :
Tìm tọa độ giao điểm của hai đường thẳng theo các bước Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm. Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$ ta được $2x - 2 = 3 - 4x \Leftrightarrow 6x = 5 \Leftrightarrow x = \dfrac{5}{6}$ Thay $x = \dfrac{5}{6}$ vào phương trình đường thẳng ${d_1}:y = 2x - 2$ ta được $y = 2.\dfrac{5}{6} - 2 = - \dfrac{1}{3}$
Câu 5 :
Cho đường thẳng $d:y = 3x - \dfrac{1}{2}$. Giao điểm của $d$ với trục tung là
Đáp án : D Phương pháp giải :
Tìm tọa độ giao điểm của hai đường thẳng theo các bước Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm. Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm. Lời giải chi tiết :
Giao điểm của đường thẳng $d$ và trục tung có hoành độ $x = 0$. Thay $x = 0$ vào phương trình $y = 3x - \dfrac{1}{2}$ ta được $y = 3.0 - \dfrac{1}{2} = - \dfrac{1}{2}$. Vậy tọa độ giao điểm cần tìm là $D\left( {0; - \dfrac{1}{2}} \right)$
Câu 6 :
Cho hàm số $y = \left( {1 - m} \right)x + m$ . Xác định $m$ để đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$
Đáp án : B Phương pháp giải :
-Giao điểm của đồ thị hàm số đã cho với trục hoành có tọa độ $M\left( {x;0} \right)$ -Thay tọa độ $M\left( {x;0} \right)$ vào hàm số, giải phương trình thu được để tìm $m$ Lời giải chi tiết :
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = - 3$ nên tọa độ giao điểm là $\left( { - 3;0} \right).$ Thay $x = - 3;y = 0$ vào $y = \left( {1 - m} \right)x + m$ ta được $\left( {1 - m} \right).\left( { - 3} \right) + m = 0 $ \( \Leftrightarrow - 3 + 3m + m = 0\) $\Leftrightarrow 4m - 3 = 0$ $\Leftrightarrow 4m=3$ $ \Leftrightarrow m = \dfrac{3}{4}.$ Vậy $m = \dfrac{3}{4}.$
Câu 7 :
Cho hàm số $y = \left( {3 - 2m} \right)x + m - 2$ . Xác định $m$ để đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$.
Đáp án : C Phương pháp giải :
-Giao điểm của đồ thị hàm số đã cho với trục tung có tọa độ $M\left( {0;y} \right)$ -Thay tọa độ $M\left( {0;y} \right)$vào hàm số, giải phương trình thu được để tìm $m$. Lời giải chi tiết :
Đồ thị hàm số cắt trục tung tại điểm có tung độ $y = - 4$ nên tọa độ giao điểm là $\left( {0; - 4} \right)$ Thay $x = 0;y = - 4$ vào $y = \left( {3 - 2m} \right)x + m - 2$ ta được $\left( {3 - 2m} \right).0 + m - 2 = - 4 \Leftrightarrow m = - 2$. Vậy $m = - 2$
Câu 8 :
Cho hàm số $y = mx - 2$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = \dfrac{1}{2}x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$.
Đáp án : A Phương pháp giải :
Để hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau tại một điểm có hoành độ \(x = {x_0}\). Bước 1. Viết phương trình hoành độ giao điểm của hai đường thẳng. Bước 2. Thay \(x = {x_0}\) vào phương trình hoành độ giao điểm để tìm \(m\). Lời giải chi tiết :
Ta có phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$: $mx - 2 = \dfrac{1}{2}x + 1$ (*) Để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có hoành độ $x = - 4$ thì $x = - 4$ thỏa mãn phương trình (*). Suy ra $m.\left( { - 4} \right) - 2 = \dfrac{1}{2}.\left( { - 4} \right) + 1 $$\Leftrightarrow - 4m - 2 = - 2 + 1 \Leftrightarrow - 4m = 1$ $\Leftrightarrow m = - \dfrac{1}{4}$.
Câu 9 :
Cho hàm số $y = \left( {m + 1} \right)x - 1$ có đồ thị là đường thẳng ${d_1}$ và hàm số $y = x + 1$ có đồ thị là đường thẳng ${d_2}$. Xác định $m$ để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = 4$.
Đáp án : C Phương pháp giải :
Để hai đường thẳng ${d_1}$ và ${d_2}$ cắt nhau tại một điểm có tung độ $y = {y_0}$. Bước 1. Thay $y = {y_0}$ vào phương trình đường thẳng đã biết để tìm ${x_0}$. Bước 2. Thay $x = {x_0}$; $y = {y_0}$ vào phương trình đường thẳng còn lại để tìm $m$. Lời giải chi tiết :
Thay $y = 4$ vào phương trình đường thẳng ${d_2}$ ta được $x + 1 = 4 \Leftrightarrow x = 3$. Suy ra tọa độ giao điểm của ${d_1}$ và ${d_2}$ là $\left( {3;4} \right)$. Thay $x = 3;y = 4$ vào phương trình đường thẳng ${d_1}$ ta được $\left( {m + 1} \right).3 - 1 = 4 \Leftrightarrow m + 1 = \dfrac{5}{3} \Leftrightarrow m = \dfrac{2}{3}$. Vậy $m = \dfrac{2}{3}$.
Câu 10 :
Với giá trị nào của m thì đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung?
Đáp án : A Phương pháp giải :
Để hai đường thẳng ${d_1}:y = ax + b$ và ${d_2}:y = a'x + b'$ cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$ Lời giải chi tiết :
Để hai đồ thị hàm số \(y = - 2x + m + 2\) và \(y = 5x + 5 - 2m\) cắt nhau tại một điểm trên trục tung thì $\left\{ \begin{array}{l} - 2 \ne 5\\m + 2 = 5 - 2m\end{array} \right.$$ \Leftrightarrow 3m = 3 \Leftrightarrow m = 1$.
Câu 11 :
Cho ba đường thẳng\({d_1}:y = - 2x;{d_2}:y = - 3x - 1;\) \({d_3}:y = x + 3.\) Khẳng định nào dưới đây là đúng?
Đáp án : D Phương pháp giải :
Để xét tính đồng quy của ba đường thẳng cho trước, ta thực hiện các bước sau Bước 1: Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho. Bước 2: Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thằng còn lại thì kết luận ba đường thẳng đó đồng quy. Lời giải chi tiết :
+) Thay tọa độ điểm $A\left( {2;1} \right)$ vào phương trình đường thẳng ${d_1}$ ta được $1 = - 2.2 \Leftrightarrow 1 = - 4$ ( vô lý) nên $A \notin {d_1}$ hay $A\left( {2;1} \right)$ không là giao điểm của ${d_1}$ và ${d_3}$. Suy ra A sai. +) Thay tọa độ điểm $B\left( {1;4} \right)$ vào phương trình đường thẳng ${d_2}$ ta được $4 = - 3.1 - 1 \Leftrightarrow 4 = - 4$ (vô lý ) Nên $B \notin {d_2}$. Suy ra C sai. +) Xét tính đồng quy của ba đường thẳng * Phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$: $ - 2x = - 3x - 1 \Leftrightarrow x = - 1$$ \Rightarrow y = - 2.\left( { - 1} \right) \Leftrightarrow y = 2$ Suy ra tọa độ giao điểm của ${d_1}$và ${d_2}$ là $\left( { - 1;2} \right)$. * Thay $x = - 1;y = 2$ vào phương trình đường thẳng ${d_3}$ ta được $2 = - 1 + 3 \Leftrightarrow 2 = 2$ (luôn đúng) Vậy ba đường thẳng trên đồng quy tại điểm $M\left( { - 1;2} \right)$.
Câu 12 :
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = x;{d_2}:y = 4 - 3x\) và \({d_3}:y = mx - 3\) đồng quy?
Đáp án : D Phương pháp giải :
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho. Bước 2. Thay tọa độ giao điểm vừa tìm được vào đường thẳng còn lại để tìm $m$. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$: $x = 4 - 3x \Leftrightarrow x = 1$$ \Rightarrow y = 1$. Suy ra giao điểm của ${d_1}$ và ${d_2}$ là $M\left( {1;1} \right)$ Để ba đường thẳng trên đồng quy thì $M \in {d_3}$ nên $1 = m.1 - 3 \Leftrightarrow m = 4$. Vậy $m = 4$.
Câu 13 :
Cho đường thẳng \(d:y = - 2x - 4\) . Gọi $A,B$ lần lượt là giao điểm của $d$ với trục hoành và trục tung. Tính diện tích tam giác $OAB.$
Đáp án : B Phương pháp giải :
Bước 1. Tìm tọa độ giao điểm $A,B$ . Bước 2. Sử dụng công thức tính diện tích tam giác $OAB$ vuông tại $O$: ${S_{OAB}} = \dfrac{{OA.OB}}{2}$ Lời giải chi tiết :
$A\left( {x;0} \right)$ là giao điểm của $d$ với trục hoành nên $0 = - 2x - 4 \Leftrightarrow x = - 2 \Rightarrow A\left( { - 2;0} \right)$ $B\left( {0;y} \right)$ là giao điểm của $d$ với trục tung nên $y = - 2.0 - 4 \Leftrightarrow y = - 4 \Rightarrow B\left( {0; - 4} \right)$. Suy ra $OA = \left| { - 2} \right| = 2;OB = \left| { - 4} \right| = 4$. Vì tam giác $OAB$ vuông tại $O$ nên ${S_{OAB}} = \dfrac{{OA.OB}}{2} = \dfrac{{2.4}}{2} = 4$ (đvdt) 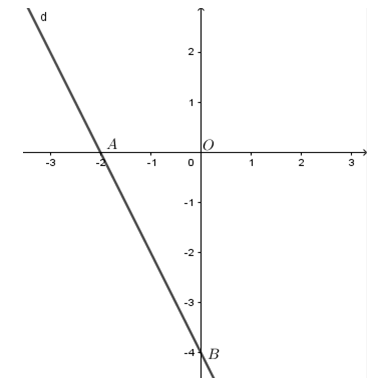
Câu 14 :
Cho đường thẳng \({d_1}:y = - x + 2\) và ${d_2}:y = 5 - 4x$. Gọi $A,B$ lần lượt là giao điểm của ${d_1}$ với ${d_2}$ và ${d_1}$ với trục hoành. Tổng hoành độ giao điểm của $A$ và $B$ là
Đáp án : C Phương pháp giải :
Tìm tọa độ giao điểm của hai đường thẳng theo các bước Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm. Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm. Lời giải chi tiết :
+) Phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$ là $ - x + 2 = 5 - 4x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1$ nên ${x_A} = 1$ +) $B\left( {{x_B};0} \right)$ là giao điểm của đường thẳng ${d_1}$ và trục hoành. Khi đó ta có $0 = - {x_B} + 2 \Rightarrow {x_B} = 2$. Suy ra tổng hoành độ ${x_A} + {x_B} = 1 + 2 = 3$.
Câu 15 :
Gọi \({d_1}\) là đồ thị hàm số \(y = mx + 1\) và \({d_2}\) là đồ thị hàm số \(y = \dfrac{1}{2}x - 2.\) Xác định giá trị của $m$ để $M\left( {2; - 1} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.
Đáp án : C Phương pháp giải :
Để $M\left( {{x_0};{y_0}} \right)$ là giao của hai đường thẳng ${d_1}$ và ${d_2}$ ta thay tọa độ điểm $M$ vào từng phương trình đường thẳng để tìm $m$. Lời giải chi tiết :
+) Nhận thấy $M \in {d_2}$. +) Ta thay tọa độ điểm $M$ vào phương trình ${d_1}$ được phương trình $ - 1 = 2.m + 1 \Leftrightarrow m = - 1$ Vậy $m = - 1$.
Câu 16 :
Với giá trị nào của m thì ba đường thẳng \({d_1}:y = \left( {m + 2} \right)x - 3;\) \({d_2}:y = 3x + 1\) và \({d_3}:y = 2x - 5\) giao nhau tại một điểm?
Đáp án : A Phương pháp giải :
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho. Bước 2. Thay tọa độ giao điểm vừa tìm được vào đường thẳng còn lại để tìm $m$. Lời giải chi tiết :
Xét phương trình hoành độ giao điểm của ${d_2}$ và ${d_3}$: $3x + 1 = 2x - 5 \Leftrightarrow x = - 6$$ \Rightarrow y = - 17$. Suy ra giao điểm của ${d_3}$ và ${d_2}$ là $M\left( { - 6; - 17} \right).$ Để ba đường thẳng trên đồng quy thì $M \in {d_1}$ nên $ - 17 = \left( {m + 2} \right).\left( { - 6} \right) - 3 \Leftrightarrow 6\left( {m + 2} \right) = 14 \Leftrightarrow m = \dfrac{1}{3}$ Vậy $m = \dfrac{1}{3}$.
Câu 17 :
Hình vẽ bên là đồ thị của hàm số nào dưới đây? 
Đáp án : B Phương pháp giải :
Sử dụng cách vẽ đồ thị hàm số Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\) Lời giải chi tiết :
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ \(\left( {1;0} \right)\) và \(\left( {2;3} \right)\) . Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số \(y = 3x - 3\) +) Thay \(x = 1;y = 0\) và vào hàm số \(y = 3x - 3\) ta được \(0 = 3 - 3 \Leftrightarrow 0 = 0\) (luôn đúng) +) Thay \(x = 2;y = 3\) và vào hàm số \(y = 3x - 3\) ta được \(3 = 3.2 - 3 \Leftrightarrow 3 = 3\) (luôn đúng) Vậy đồ thị hàm số \(y = 3x - 3\) là đường thẳng như hình vẽ.
|



















Danh sách bình luận