Trắc nghiệm Bài 7: Tứ giác nội tiếp Toán 9Đề bài
Câu 1 :
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định sai? 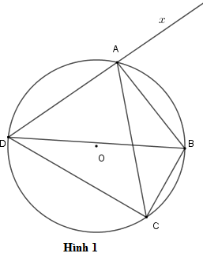
Câu 2 :
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp? 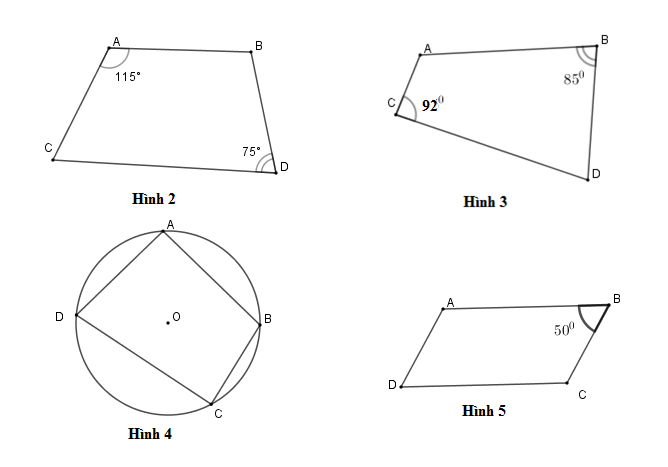
Câu 3 :
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
Câu 4 :
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
Câu 5 :
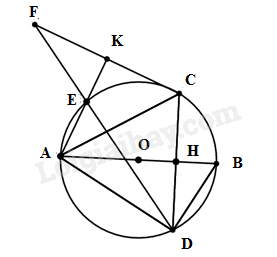
Cho đường tròn $\left( O \right)$ đường kính $AB$ . Gọi $H$ là điểm nằm giữa $O$ và $B$. Kẻ dây $CD$ vuông góc với $AB$ tại $H$ . Trên cung nhỏ $AC$ lấy điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ tại $F$. Chọn câu đúng:
Cho hình vẽ dưới đây 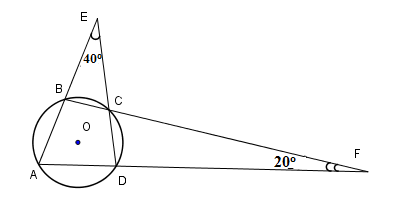 Câu 6
Khi đó mệnh đề đúng là
Câu 7
Số đo góc \(\widehat {BAD}\) là
Câu 8 :
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
Câu 9 :
Cho tam giác $ABC$ nhọn nội tiếp đường tròn $\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\)). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng:
Cho đường tròn $(O)$ đường kính $AB.$ Gọi $H$ là điểm nằm giữa $O$ và $B.$ Kẻ dây $CD$ vuông góc với $AB$ tại $H$. Trên cung nhỏ $AC$ lấy điểm $E,$ kẻ $CK \bot AE$ tại $K.$ Đường thẳng $DE$ cắt $CK$ tại $F.$ Câu 10
Tứ giác \(AHCK\) là
Câu 11
Tích \(AH.AB\) bằng
Câu 12 :
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
Trên các cạnh \(BC,CD\) của hình vuông \(ABCD\) ta lấy lần lượt các điểm \(M,N\) sao cho \(\widehat {MAN} = {45^0}\). Đường thẳng \(BD\) cắt các đường thẳng \(AM,AN\) tương ứng tại các điểm \(P,Q\). Câu 13
$\left( I \right):$ Tứ giác \(ABMQ\) nội tiếp; $\left( {II} \right):$ Tứ giác \(ADNP\) nội tiếp. Chọn kết luận đúng.
Câu 14
Năm điểm nào sau đây cùng thuộc một đường tròn?
Câu 15 :
Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
Câu 16 :
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
Câu 17 :
Cho nửa $(O)$ đường kính $AB.$ Lấy $M \in OA(M \ne O,A).$ Qua $M$ vẽ đường thẳng $d$ vuông góc với $AB.$ Trên $d$ lấy $N$ sao cho $ON > R.$ Nối $NB$ cắt $(O)$ tại $C.$ Kẻ tiếp tuyến $NE$ với $(O)$ ($E$ là tiếp điểm, $E$ và $A$ cùng thuộc nửa mặt phẳng bờ $d$). Gọi $H$ là giao điểm của $AC$ và $d$, $F$ là giao điểm của $EH$ và đường tròn $(O)$. Chọn khẳng định sai?
Câu 18 :
Cho nửa đường tròn tâm \(O,\) đường kính \(AB = 2R.\) Đường thẳng qua \(O\) và vuông góc \(AB\) cắt cung \(AB\) tại \(C.\) Gọi \(E\) là trung điểm \(BC.\,\,AE\) cắt nửa đường tròn \(O\) tại \(F.\) Đường thẳng qua \(C\) và vuông góc $AF$ tại \(G\) cắt \(AB\) tại $H.$ Khi đó góc \(\widehat {OGH}\) có số đo là:
Câu 19 :
Cho hình vẽ. Khi đó đáp án đúng là 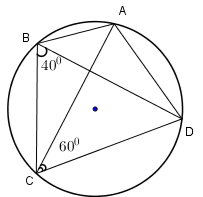
Câu 20 :
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) và $\widehat A = \partial \;\;\left( {0 < \partial < {{90}^0}} \right)$. Gọi M là một điểm tùy ý trên cung nhỏ AC vẽ tia Bx vuông góc với AM cắt tia CM tại D. Số đo góc $\widehat {BDM}$ là:
Câu 21 :
Tứ giác ABCD nội tiếp (O) . Hai đường chéo AC và BD cắt nhau tại I. Vẽ đường tròn ngoại tiếp tam giác ABI. Tiếp tuyến của đường tròn này tại I cắt AD và BC lần lượt M và N. Chọn câu sai:
Câu 22 :
Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\) bán kính bằng \(a.\) Biết rằng \(AC \bot BD.\) Khi đó để \(AB + CD\) đạt giá trị lớn nhất thì
Câu 23 :
Cho tam giác \(ABC\) không cân, nội tiếp đường tròn \(\left( O \right),\,\,BD\) là đường phân giác của góc \(\widehat {ABC}.\) Đường thẳng \(BD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(E.\) Đường tròn \(\left( {{O_1}} \right)\) đường kính \(DE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Khi đó đường thẳng đối xứng với đường thẳng \(BF\) qua đường thẳng \(BD\) cắt \(AC\) tại \(N\) thì:
Lời giải và đáp án
Câu 1 :
Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) (hình \(1\) ). Chọn khẳng định sai? 
Đáp án : C Phương pháp giải :
Sử dụng kiến thức hai góc cùng chắn một cung thì bằng nhau. Sử dụng tính chất tứ giác nội tiếp: Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ\) Lời giải chi tiết :
Vì tứ giác \(ABCD\) là tứ giác nội tiếp nên \(\widehat {BDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung \(BC\) ) \(\widehat {ABC} + \widehat {ADC} = 180^\circ \) (tổng hai góc đối bằng \(180^\circ \) ) \(\widehat {DAB}\) và \(\widehat {BAx}\) là hai góc kề bù nhưng \(\widehat {DAB} \ne 90^\circ\) nên \(\widehat {DAB} \ne \widehat {BAx}\) \(\widehat {BCA} = \widehat {BDA}\) (hai góc nội tiếp cùng chắn cung \(AB\) ) Phương án A, B, D đúng
Câu 2 :
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp? 
Đáp án : C Phương pháp giải :
Tứ giác có tổng một cặp góc đối bằng \({180^0}\) là tứ giác nội tiếp. Tứ giác có 4 đỉnh cùng thuộc một đường tròn là tứ giác nội tiếp. Lời giải chi tiết :
Hình 2 sai vì \(\widehat A + \widehat C = {115^0} + {75^0} = {190^0} \ne {180^0}\) . Hình 3 sai vì \(\widehat C + \widehat B = {92^0} + {85^0} = {177^0} \ne {180^0}\) . Hình 5 sai vì \(\widehat D + \widehat B = {50^0} + {50^0} = {100^0} \ne {180^0}\) . Hình 4 đúng vì tứ giác này có \(4\) đỉnh cùng thuộc một đường tròn.
Câu 3 :
Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(BC.\) Lấy điểm \(A\) trên tia đối của tia \(CB.\) Kẻ tiếp tuyến $AF,Bx$ của nửa đường tròn \(\left( O \right)\) (với \(F\) là tiếp điểm). Tia \(AF\) cắt tia \(Bx\) của nửa đường tròn tại \(D.\) Khi đó tứ giác \(OBDF\) là:
Đáp án : B Phương pháp giải :
Tứ giác có tổng một cặp góc đối bằng \({180^0}\) là tứ giác nội tiếp. Lời giải chi tiết :
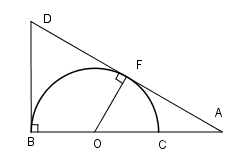 Ta có \(\widehat {DBO} = {90^0}\) và \(\widehat {DFO} = {90^0}\) ( tính chất tiếp tuyến). Tứ giác \(OBDF\) có \(\widehat {DBO} + \widehat {DFO} = {90^0} + {90^0} = {180^0}\) nên nội tiếp được trong một đường tròn.
Câu 4 :
Tứ giác $ABCD$ nội tiếp đường tròn có hai cạnh đối $AB$ và $CD$ cắt nhau tại $M$ và $\widehat {BAD} = {70^0}$ thì $\widehat {BCM} = ?$
Đáp án : C Phương pháp giải :
Áp dụng tính chất tứ giác nội tiếp có tổng hai góc đối diện bằng \({180^0}.\) Lời giải chi tiết :
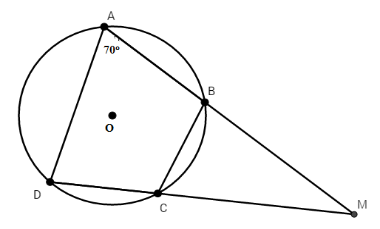 Tứ giác $ABCD$ nội tiếp nên có: $\widehat {DAB} + \widehat {BCD} = {180^\circ}$ suy ra $\widehat {BCD} = {180^\circ} - {70^\circ} = {110^\circ}$ Mà $\widehat {BCD} + \widehat {BCM} = {180^\circ}$ (kề bù) Do đó $\widehat {BCM} = {180^\circ} - {110^\circ} = {70^\circ}$ Chú ý
Các em có thể sử dụng tính chất : “ Trong một tứ giác nội tiếp góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.”
Câu 5 :
Cho đường tròn $\left( O \right)$ đường kính $AB$ . Gọi $H$ là điểm nằm giữa $O$ và $B$. Kẻ dây $CD$ vuông góc với $AB$ tại $H$ . Trên cung nhỏ $AC$ lấy điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ tại $F$. Chọn câu đúng:
Đáp án : A Phương pháp giải :
- Chứng minh tứ giác có bốn đỉnh cách đều một điểm nên là tứ giác nội tiếp. - Tứ giác nội tiếp có tổng hai góc đối bằng \(180^\circ\). - Chứng minh hai tam giác đồng dạng suy ra tỉ số giữa các cạnh tương ứng. Lời giải chi tiết :
Xét tam giác AHC có $\widehat {AHC} = {90^0}$ (CD vuông góc AB) nên tam giác AHC nội tiếp đường tròn đường kính AC. Xét tam giác AKC có $\widehat {AKC} = {90^0}$ (AK vuông góc CF) nên tam giác AKC nội tiếp đường tròn đường kính AC. Do đó tứ giác AHCK là tứ giác nội tiếp (do A, H, K, C cùng thuộc đường tròn đường kính AC) suy ra phương án A đúng, B sai. Do đó \(\widehat {EAO} + \widehat {HCK} = {180^0}\) (tính chất tứ giác nội tiếp) suy ra phương án C sai. Xét tam giác vuông \(ADB\) và \(AHD) có \(\widehat {DAB}\) chung \(\widehat {ADB} = \widehat {AHD} \left( = 90^\circ \right)\) suy ra \(\Delta ADB \backsim \Delta AHD\) (g.g) suy ra \(\frac{AD}{AB} = \frac{AH}{AD}\) do đó \(AH.AB = A{D^2}\) nên phương án D sai. Cho hình vẽ dưới đây  Câu 6
Khi đó mệnh đề đúng là
Đáp án : C Phương pháp giải :
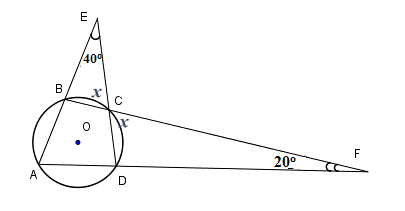
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\) Sử dụng tính chất góc ngoài của tam giác và tính chất hai góc đối diện của tứ giác nội tiếp để tính x. Từ đó tính số đo góc ABC. Lời giải chi tiết :
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\) Theo tính chất góc ngoài tam giác vào tam giác BCE và tam giác CDF ta có: \(\widehat {ABC} = x + {40^0}\,\,\left( 1 \right);\widehat {ADC} = x + {20^0}\,\,\left( 2 \right)\) Lại có \(\widehat {ABC} + \widehat {ADC} = {180^0}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp ABCD). Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được: \(\left( {x + {{40}^0}} \right) + \left( {x + {{20}^0}} \right) = {180^0} \) \(x + {{40}^0} + x + {{20}^0} = {180^0} \) \(2x = {120^0} \) Suy ra \(x = {60^0}\) . Từ \(\left( 1 \right)\) ta có \(\widehat {ABC} = {60^0} + {40^0} = {100^0}\) . Câu 7
Số đo góc \(\widehat {BAD}\) là
Đáp án : D Phương pháp giải :
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\) Sử dụng tính chất góc ngoài của tam giác và tính chất hai góc đối diện của tứ giác nội tiếp để tính x. Sử dụng tính chất hai góc kề bù và hai góc đối diện của tứ giác nội tiếp để tính góc BAD. Lời giải chi tiết :
Ta có \(\widehat {BCE} = \widehat {DCF}\) (hai góc đối đỉnh). Đặt \(x = \widehat {BCE} = \widehat {DCF}.\) Theo tính chất góc ngoài tam giác vào tam giác BCE và tam giác CDF ta có: \(\widehat {ABC} = x + {40^\circ}\,\,\left( 1 \right);\widehat {ADC} = x + {20^\circ}\,\,\left( 2 \right)\) Lại có \(\widehat {ABC} + \widehat {ADC} = {180^\circ}\,\,\left( 3 \right)\) (hai góc đối diện của tứ giác nội tiếp ABCD). Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta nhận được: \(\left( {x + {{40}^\circ}} \right) + \left( {x + {{20}^\circ}} \right) = {180^\circ} \) \(x + {{40}^\circ} + x + {{20}^\circ} = {180^\circ} \) \(2x = {120^\circ} \) Suy ra \(x = {60^\circ}\) . Do \(\widehat {BCD},\,\widehat {BCE}\) là hai góc kề bù nên \(\widehat {BCD} + \,\widehat {BCE} = {180^\circ}\) suy ra \(\widehat {BCD} = {180^\circ} - {60^\circ} = {120^\circ}\) Ta lại có \(\widehat {BAD},\,\widehat {BCD}\) là hai góc đối diện của tứ giác nội tiếp nên $\widehat {BAD} + \,\widehat {BCD} = {180^\circ}$ suy ra $\widehat {BAD} = {180^\circ} - {120^\circ} = {60^\circ}$ Cách khác: Xét tam giác \(ADE\), theo định lí về tổng ba góc trong tam giác, ta có: \(\widehat {BAD} + \widehat {CDA} + \widehat {AED} = {180^\circ}\) \( \widehat {BAD} + \widehat {CDA} + {40^\circ} = {180^\circ}\) \( \widehat {BAD} + \widehat {CDA} = {140^\circ}\,(1*)\) Xét tam giác \(ABF\), theo định lí về tổng ba góc trong tam giác, ta có: \(\widehat {BAD} + \widehat {CBA} + \widehat {AFB} = {180^\circ}\) \(\widehat {BAD} + \widehat {CBA} + {20^\circ} = {180^\circ}\) \(\widehat {BAD} + \widehat {CBA} = {160^\circ}\,(2*)\) Vì tứ giác \(ABCD\) nội tiếp đường tròn \((O)\) nên \(\widehat {ADC} + \widehat {CBA} = {180^\circ}\) (3*) (tổng hai góc đối bằng \(180^\circ\)) Từ \((1*), (2*)\) và (3*) ta có: \(\widehat {BAD} + \widehat {ADC} + \widehat {BAD} + \widehat {CBA} = {140^\circ} + {160^\circ}\) \(2\widehat {BAD} + \left( {\widehat {ADC} + \widehat {CBA}} \right) = {300^\circ}\) \(2\widehat {BAD} + {180^\circ} = {300^\circ}\) \(2\widehat {BAD} = {120^\circ}\) \(\widehat {BAD} = {60^\circ}\)
Câu 8 :
Cho \(\Delta ABC\) cân tại \(A\) có \(\widehat {BAC} = {120^0}.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A\), lấy \(D\) sao cho \(BCD\) là tam giác đều. Khi đó
Đáp án : B Phương pháp giải :
Chứng minh tam giác ABD và tam giác ACD là hai tam giác vuông nội tiếp đường tròn đường kính AD nên là tứ giác nội tiếp. Lời giải chi tiết :
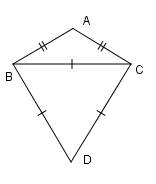 Ta có $\Delta BCD$ là tam giác đều nên \(\widehat {DCB} = {60^0}\,\,\left( 1 \right).\) Mặt khác \(\Delta ABC\) là tam giác cân tại \(A\) có $\widehat {BAC} = {120^0}$. Áp dụng định lí tổng ba góc trong một tam giác bằng \({180^0}\) nên \(\widehat {ACB} = \widehat {ABC}\) và \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\) nên \(\widehat {ACB} = {30^0}\,\,\,\,\left( 2 \right)\) . Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có \(\widehat {ACD} = \widehat {DCB} + \widehat {BCA} = {60^0} + {30^0} = {90^0}\). Tam giác ACD có \(\widehat {ACD} = {90^0}\) nên nội tiếp đường tròn đường kính AD. (3) Chứng minh tương tự ta có \(\widehat {ABD} = {90^0}\). Tam giác ABD có \(\widehat {ABD} = {90^0}\) nên nội tiếp đường tròn đường kính AD. (4) Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) suy ra tứ giác \(ABDC\) là tứ giác nội tiếp (vì bốn đỉnh A, B, C, D cùng thuộc đường tròn đường kính AD).
Câu 9 :
Cho tam giác $ABC$ nhọn nội tiếp đường tròn $\left( O \right)$ . $M$ là điểm thuộc cung nhỏ $AC$ (cung \(CM < \) cung \(AM\)). Vẽ $MH$ vuông góc với $BC$ tại $H$ , vẽ $MI$ vuông góc với $AC$ tại $I$ . Chọn câu đúng:
Đáp án : D Phương pháp giải :
Tứ giác có 4 đỉnh thuộc một đường tròn thì nội tiếp đường tròn đó. Lời giải chi tiết :
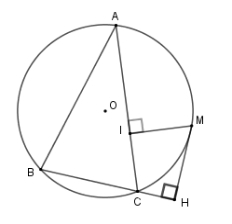 Tam giác MIC có $\widehat {MIC} = {90^0}$ ($MI$ vuông góc với $AC$) nên là tam giác vuông nội tiếp đường tròn đường kính MC. Tam giác MHC có $\widehat {MHC} = {90^0}$ ($MH$ vuông góc với $BC$) nên là tam giác vuông nội tiếp đường tròn đường kính MC. Suy ra tứ giác $IMHC$ nội tiếp (vì 4 đỉnh I, M, H, C cùng thuộc đường tròn đường kính BC) nên đáp án D đúng và đáp án C sai. Tuy nhiên tứ giác $IMHC$ chưa đủ điều kiện để là hình chữ nhật và hình vuông nên đáp án A, B chưa chính xác. Cho đường tròn $(O)$ đường kính $AB.$ Gọi $H$ là điểm nằm giữa $O$ và $B.$ Kẻ dây $CD$ vuông góc với $AB$ tại $H$. Trên cung nhỏ $AC$ lấy điểm $E,$ kẻ $CK \bot AE$ tại $K.$ Đường thẳng $DE$ cắt $CK$ tại $F.$ Câu 10
Tứ giác \(AHCK\) là
Đáp án : A Phương pháp giải :
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. Lời giải chi tiết :
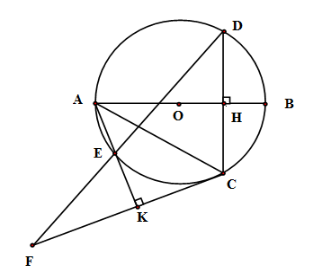 Xét tam giác AHC và tam giác AKC có \(\widehat {AHC} = 90^\circ \left( {AB \bot CD} \right);\widehat {AKC} = 90^\circ \left( {AK \bot FC} \right)\) nên tam giác AHC và AKC vuông và nội tiếp đường tròn đường kính AC. Do đó tứ giác \(AHCK\) nội tiếp (bốn đỉnh A, H, C, K cùng thuộc đường tròn đường kính AC). Câu 11
Tích \(AH.AB\) bằng
Đáp án : D Phương pháp giải :
Sử dụng góc nội tiếp chắn nửa đường tròn và chứng minh \(\Delta ADB \backsim \Delta AHD\) (g.g). Lời giải chi tiết :
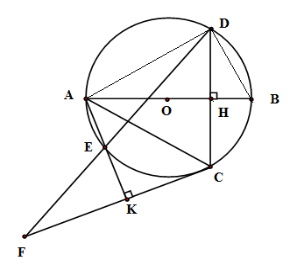 Xét tam giác \(ADB\) có \(\widehat {ADB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(\Delta ADB\) vuông tại \(D\). Xét tam giác ADB và tam giác AHD có: \(\widehat A\) chung \(\widehat {ADB} = \widehat {AHD} \left( = 90 ^\circ \right) \) suy ra \(\Delta ADB \backsim \Delta AHD\) (g.g) suy ra \(\frac{AD}{AB} = \frac{AH}{AD}\) Do đó \(A{D^2} = AH.AB\) Mà \(AD \ne BD;AD < AB\) nên phương án A, B, C sai.
Câu 12 :
Cho \(\Delta ABC\) vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:
Đáp án : D Phương pháp giải :
Góc nội tiếp chắn nửa đường tròn là góc vuông. Dấu hiệu nhận biết tứ giác nội tiếp: +) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\) +) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\) +) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác. +) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. Lời giải chi tiết :
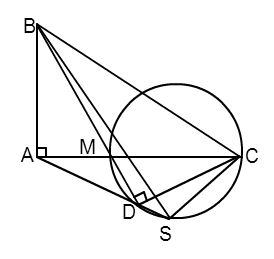 +) Ta có: \(\widehat {MDC}\) là góc nội tiếp chắn nửa đường tròn đường kính $MC$ \( \Rightarrow \widehat {MDC} = {90^0}\) (tính chất góc nội tiếp). Xét tứ giác $ABCD$ ta có: Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc \({90^0}.\) \( \Rightarrow \) $ABCD$ là tứ giác nội tiếp (dhnb) \( \Rightarrow \) phương án A đúng. +) Xét tứ giác $ABCD$ nội tiếp ta có\(\widehat {ABD} = \widehat {ACD}\) (cùng nhìn đoạn $AD$ )\( \Rightarrow \) phương án B đúng. +) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn. \( \Rightarrow \) Tứ giác $MCSD$ là tứ giác nội tiếp. \( \Rightarrow \widehat {ADM} = \widehat {SCM}\) (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$ Vì tứ giác $ABCD$ nội tiếp (cmt) \( \Rightarrow \widehat {ACB} = \widehat {ADB}\) (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$ Từ $\left( 1 \right)$ và $\left( 2 \right)$ \( \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).\) Hay $CA$ là phân giác của \(\widehat {SCB} \Rightarrow \) phương án C đúng. +) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp \( \Rightarrow \widehat {ASB} = \widehat {BCA}\) (hai góc cùng nhìn đoạn $AB$ ). Mà \(\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}\) (xét trong đường tròn đường kính $CM$ ) \( \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow \) tứ giác $ABCS$ không là tứ giác nội tiếp \( \Rightarrow \)phương án D sai. Trên các cạnh \(BC,CD\) của hình vuông \(ABCD\) ta lấy lần lượt các điểm \(M,N\) sao cho \(\widehat {MAN} = {45^0}\). Đường thẳng \(BD\) cắt các đường thẳng \(AM,AN\) tương ứng tại các điểm \(P,Q\). Câu 13
$\left( I \right):$ Tứ giác \(ABMQ\) nội tiếp; $\left( {II} \right):$ Tứ giác \(ADNP\) nội tiếp. Chọn kết luận đúng.
Đáp án : A Phương pháp giải :
Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\) Lời giải chi tiết :
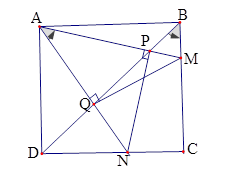 Xét hình vuông \(ABCD\) có \(\widehat {DBC} = \widehat {BDC} = 45^\circ \) (tính chất) Xét tứ giác \(ABMQ\) có \(\widehat {QAM} = \widehat {QBM} = 45^\circ \) mà hai đỉnh \(A\) và \(B\) cùng nhìn đoạn thẳng \(MQ\) nên \(ABMQ\) là tứ giác nội tiếp. Xét tứ giác \(APND\) có \(\widehat {PAN} = \widehat {PDN} = 45^\circ \) mà hai đỉnh \(A\) và ${\rm{D}}$ cùng nhìn đoạn thẳng \(PN\) nên \(APND\) là tứ giác nội tiếp. Câu 14
Năm điểm nào sau đây cùng thuộc một đường tròn?
Đáp án : B Phương pháp giải :
Sử dụng các đỉnh cùng nhìn cạnh \(AB\) dưới một góc vuông thì nằm trên đường tròn đường kính \(AB\) Lời giải chi tiết :
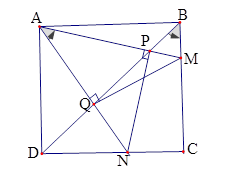 Từ kết quả câu trước ta suy ra \(\widehat {ADP} = \widehat {ANP} = {45^0},\widehat {QAM} = \widehat {QBM} = {45^0}\)\( \Rightarrow NP \bot AM,MQ \bot AN\). Tập hợp các điểm \(P,Q,C\) nhìn đoạn \(MN\) dưới một góc vuông, nên các điểm này nằm trên đường tròn đường kính \(MN\).
Câu 15 :
Cho đường tròn $\left( O \right)$ đường kính $AB$. Gọi $I$ là trung điểm của $OA$ . Dây $CD$ vuông góc với $AB$ tại $I$. Lấy $K$ tùy ý trên cung $BC$ nhỏ, $AK$ cắt $CD$ tại $H$. Khẳng định nào đúng ?
Đáp án : A Phương pháp giải :
Góc nội tiếp chắn nửa đường tròn là góc vuông. Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. Lời giải chi tiết :
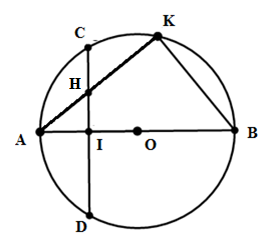 Ta có: \(\widehat {AKB}\) là góc nội tiếp chắn nửa đường tròn (O) suy ra \( \widehat {AKB} = {90^0}.\) Tam giác HKB có \(\widehat {HKB} = {90^0}\) và tam giác HIB có \(\widehat {HIB} = {90^0}\left( {do\;\;CD \bot AB } \right)\) nên tam giác HKB và tam giác HIB vuông và nội tiếp đường tròn đường kính HB. Do đó tứ giác HKBI là tứ giác nội tiếp (bốn đỉnh H, K, B, I cùng thuộc đường tròn đường kính HB). Vậy A đúng, B sai. Lại có \(\widehat {KBA} < {90^0}\) do \(\Delta AKB\) vuông tại \(K\) nên \(KBIH\) không là hình chữ nhật. Do đó C sai.
Câu 16 :
Cho tam giác $ABC$ vuông tại $A$ và điểm $D$ nằm giữa $A$ và $B$ . Đường tròn đường kính $BD$ cắt $BC$ tại $E$. Các đường thẳng $CD$ , $AE$ lần lượt cắt đường tròn tại các điểm thứ hai là $F$ và $G$. Khi đó, kết luận không đúng là:
Đáp án : C Phương pháp giải :
Góc nội tiếp chắn nửa đường tròn là góc vuông. Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. Lời giải chi tiết :
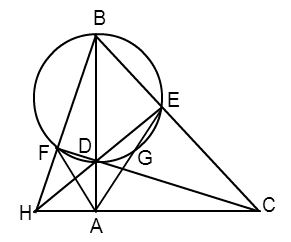 +) Xét đường tròn đường kính $BD$ có góc $BED$ là góc nội tiếp chắn nửa đường tròn nên \( \widehat {BED} = {90^0}.\) Xét \(\Delta ABC\) và \(\Delta BED\) ta có: \(\widehat {DBE}\;\;chung\) và \(\widehat {BAC} = \widehat {BED} = {90^0}\) suy ra $\Delta ABC\backsim\Delta EBD\;\left( {g - g} \right)$ Vậy A đúng. +) Do tam giác ADC vuông tại A (\(\widehat {DAC} = 90^0\)) và tam giác DEC vuông tại E (\(\widehat {DEC} = 90^0\)) nên tam giác ADC và tam giác DEC nội tiếp đường tròn đường kính DC. Do đó tứ giác $ADEC$ là tứ giác nội tiếp. Vậy B đúng. +) Chứng minh tương tự ta được tứ giác $AFBC$ là tứ giác nội tiếp. Vậy C sai. +) Gọi giao điểm của $BF$ và $AC$ là $H$ . Xét tam giác $BHC$ có hai đường cao $CF$ và $BA$ cắt nhau tại $D$. Do đó $D$ là trực tâm của tam giác $BHC$ Mà $DE = \bot AB$ nên $DE$ là đường cao của tam giác $BHC$ hay $H,E,D$ thẳng hàng. Suy ra $DE,AC$ và $BF$ đồng quy tại $H$ suy ra D đúng.
Câu 17 :
Cho nửa $(O)$ đường kính $AB.$ Lấy $M \in OA(M \ne O,A).$ Qua $M$ vẽ đường thẳng $d$ vuông góc với $AB.$ Trên $d$ lấy $N$ sao cho $ON > R.$ Nối $NB$ cắt $(O)$ tại $C.$ Kẻ tiếp tuyến $NE$ với $(O)$ ($E$ là tiếp điểm, $E$ và $A$ cùng thuộc nửa mặt phẳng bờ $d$). Gọi $H$ là giao điểm của $AC$ và $d$, $F$ là giao điểm của $EH$ và đường tròn $(O)$. Chọn khẳng định sai?
Đáp án : D Phương pháp giải :
* Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: +) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\) +) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\) +) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác. +) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. * Sử dụng tam giác đồng dạng. Lời giải chi tiết :
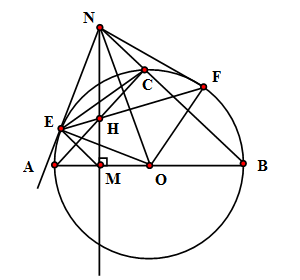 +) Vì \(\widehat {NEO} = \widehat {NMO} = 90^\circ \Rightarrow NEMO\) là tứ giác nội tiếp nên bốn điểm $O,E,M,N$ cùng thuộc một đường tròn \( \Rightarrow \) Phương án A đúng. +) \(\widehat {NEC} = \widehat {CBE} = \dfrac{1}{2}\) số đo cung $CE \Rightarrow \Delta NEC\backsim\Delta NBE\left( {g - g} \right) \Rightarrow \dfrac{{NE}}{{NB}} = \dfrac{{NC}}{{NE}}$ \( \Rightarrow NB.NC = N{E^2}\) \( \Rightarrow \) Phương án B đúng. +) Hai tam giác vuông $\Delta NCH\backsim\Delta NMB\left( {g - g} \right) $ $\Rightarrow \dfrac{{NC}}{{NM}} = \dfrac{{NH}}{{NB}} $ $\Rightarrow NC.NB=NH.NM$ Từ đó $\Delta NEH\backsim\Delta NME\left( {c-g -c} \right) \Rightarrow \widehat {NEH} = \widehat {EMN}$ \( \Rightarrow \) Phương án C đúng. +) \(\widehat {EMN} = \widehat {EON}\) (tứ giác \(NEMO\) nội tiếp) \( \Rightarrow \widehat {NEH} = \widehat {NOE}\) Mà góc $ENO$ phụ với góc $EON$ nên góc $ENO$ cũng phụ với góc $NEH$ \(\Rightarrow EH \bot NO\) \( \Rightarrow \Delta OEF\) cân có \(ON\) là phân giác \( \Rightarrow \widehat {EON} = \widehat {NOF} \Rightarrow \widehat {NEF} = \widehat {NOF}\) nên tứ giác \(NEOF\) nội tiếp \( \Rightarrow \widehat {NFO} = 180^\circ - \widehat {NEO} = 90^\circ \) . \( \Rightarrow \) Phương án D sai.
Câu 18 :
Cho nửa đường tròn tâm \(O,\) đường kính \(AB = 2R.\) Đường thẳng qua \(O\) và vuông góc \(AB\) cắt cung \(AB\) tại \(C.\) Gọi \(E\) là trung điểm \(BC.\,\,AE\) cắt nửa đường tròn \(O\) tại \(F.\) Đường thẳng qua \(C\) và vuông góc $AF$ tại \(G\) cắt \(AB\) tại $H.$ Khi đó góc \(\widehat {OGH}\) có số đo là:
Đáp án : A Phương pháp giải :
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn. Các góc nội tiếp cùng chắn một cung thì bằng nhau. Lời giải chi tiết :
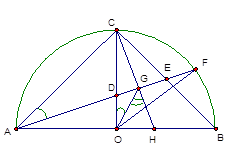 Theo giả thiết ta có \(OC \bot AB,\,CG \bot AG\) nên ta suy ra \(\widehat {AOC} = \widehat {AGC} = {90^0}.\) Suy ra tam giác AOC vuông tại O nên nội tiếp đường tròn đường kính AC; tam giác AGC vuông tại G và nội tiếp đường tròn đường kính AC. Mà \(\Delta OAC\) vuông cân tại O nên \(\widehat {OCA} = {45^0}.\) Suy ra \(\widehat {OGA} = {45^0}.\) Ta lại có \(\widehat {OGH} + \widehat {OGA} = \widehat {HGA} = \widehat {AGC} = {90^0} \) Suy ra \(\widehat {OGH} = {90^0} - \widehat {OGA} = {90^0} - {45^0} = {45^0}.\) Do đó \(\widehat {OGH} = {45^0}\)
Câu 19 :
Cho hình vẽ. Khi đó đáp án đúng là 
Đáp án : B Phương pháp giải :
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau. - Tổng ba góc trong một tam giác bằng \({180^0}\). Lời giải chi tiết :
Do tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O,\) nên ta có $\widehat {CAD} = \widehat {CBD}$ (cùng chắn cung \(CD\) ). Do đó ta có \(\widehat {CAD} = {40^0}.\) Áp dụng định lí tổng ba góc trong một tam giác bằng \({180^0}\) vào tam giác ACD, ta có: $\widehat {CAD} + \widehat {ACD} + \widehat {ADC} = {180^0}$ Suy ra \( \widehat {ADC} = {180^0} - \left( {\widehat {CAD} + \widehat {ACD}} \right) \) \(= {180^0} - \left( {{{40}^0} + {{60}^0}} \right) = {80^0}\)
Câu 20 :
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) và $\widehat A = \partial \;\;\left( {0 < \partial < {{90}^0}} \right)$. Gọi M là một điểm tùy ý trên cung nhỏ AC vẽ tia Bx vuông góc với AM cắt tia CM tại D. Số đo góc $\widehat {BDM}$ là:
Đáp án : A Phương pháp giải :
+) Áp dụng quan hệ số đo góc nội tiếp và cung bị chắn. +) Tính chất trong tứ giác nội tiếp tổng hai góc đối diện bằng \({180^0}.\) Lời giải chi tiết :
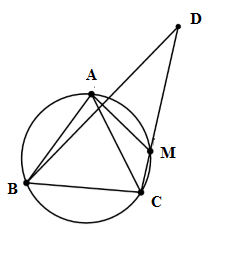 Xét tam giác ABC cân tại A và \(\widehat A = {60^0} \Rightarrow \widehat B = \widehat C = \dfrac{{{{180}^0} - \widehat A}}{2} = \dfrac{{{{180}^0} - \partial }}{2} = {90^0} - \dfrac{\partial }{2}.\) Ta có tứ giác AMCB là tứ giác nội tiếp (4 điểm A, M, B, C cùng thuộc (O)). \( \Rightarrow \widehat {AMC} = {180^0} - \widehat {ABC} \)\(= {180^0} - \left( {{{90}^0} - \dfrac{\partial }{2}} \right) = {90^0} + \dfrac{\partial }{2}.\) \( \Rightarrow \widehat {DMA} = \widehat {ABC} = {90^0} - \dfrac{\partial }{2}\) (tính chất tứ giác nội tiếp). Gọi I là giao điểm của AM và BD. \( \Rightarrow \Delta DMI\) vuông tại I. \( \Rightarrow \widehat {BDM} = {90^0} - \widehat {AMD} \)\(= {90^0} - \left( {{{90}^0} - \dfrac{\partial }{2}} \right) = \dfrac{\partial }{2}.\)
Câu 21 :
Tứ giác ABCD nội tiếp (O) . Hai đường chéo AC và BD cắt nhau tại I. Vẽ đường tròn ngoại tiếp tam giác ABI. Tiếp tuyến của đường tròn này tại I cắt AD và BC lần lượt M và N. Chọn câu sai:
Đáp án : C Phương pháp giải :
Góc nội tiếp chắn nửa đường tròn là góc vuông. Dấu hiệu nhận biết tứ giác nội tiếp: +) Tứ giác có tổng hai góc đối diện bằng \({180^0}.\) +) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha .\) +) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác. +) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó. Lời giải chi tiết :
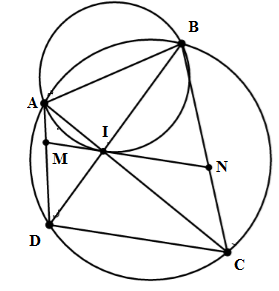 Xét đường tròn ngoại tiếp tam giác ABI ta có: \(\widehat {BAI}\) là góc nội tiếp chắn cung BI. \(\widehat {BIN}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung BI. \( \Rightarrow \widehat {BAI} = \widehat {BIN}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BI). Xét đường tròn (O) ta có: \(\widehat {BDC} = \widehat {BAC}\) (hai góc nội tiếp cùng chắn cung BC). \( \Rightarrow \widehat {BIN} = \widehat {BDC}\left( { = \widehat {BAC}} \right)\) Lại có hai góc này ở vị trí đồng vị \( \Rightarrow IN//CD\;\;hay\;\;MN//CD\;\;\left( {dpcm} \right).\) \( \Rightarrow \) đáp án A đúng. Do MN//CD nên \(\widehat {MNC} + \widehat {NCD} = {180^0}\)(trong cùng phía) Mà do tứ giác ABCD nội tiếp nên \(\widehat {MAB} + \widehat {NCD} = {180^0}\) => \(\widehat {MNC} = \widehat {NAB}\) => Tứ giác ABNM nội tiếp (góc trong bằng góc ngoài tại đỉnh đối diện) \( \Rightarrow \) Đáp án B đúng. +) Ta có: \(IN//CD\;\;\left( {cmt} \right) \Rightarrow \) INCD là hình thang \( \Rightarrow \) đáp án D đúng.
Câu 22 :
Cho tứ giác \(ABCD\) nội tiếp đường tròn tâm \(O\) bán kính bằng \(a.\) Biết rằng \(AC \bot BD.\) Khi đó để \(AB + CD\) đạt giá trị lớn nhất thì
Đáp án : B Phương pháp giải :
Vẽ đường kính \(CE\) của đường tròn \(\left( O \right).\) Chứng minh \(AB = DE\) rồi đánh giá \({\left( {AB + CD} \right)^2}\) đạt GTLN dựa vào bđt Cô-si, từ đó suy ra điều kiện thỏa mãn bài toán. Lời giải chi tiết :
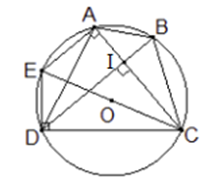 Vẽ đường kính \(CE\) của đường tròn \(\left( O \right).\) Ta có \(\widehat {EAC} = {90^0},\,\widehat {EDC} = {90^0}\) (góc nội tiếp chắn đường kính \(EC\) ). Từ đó ta có \(AE \bot AC.\) Mặt khác theo giả thiết \(AC \bot BD.\) Kéo theo \(AE//BD.\) Vậy \(AEDB\) là hình thang. Do hình thang \(AEDB\) nội tiếp \(\left( O \right)\) nên nói phải là hình thang cân. Kéo theo \(AB = DE\) (các cạnh bên hình thang cân). Từ đó ta có \(A{B^2} + C{D^2} = D{E^2} + D{C^2} = E{C^2} = {\left( {2a} \right)^2} = 4{a^2}\) (do \(\Delta EDC\) vuông tại \(D).\) Áp dụng bất đẳng thức Cô-si cho \(\left( {A{B^2},B{D^2}} \right)\) ta có $A{B^2} + B{D^2} \ge 2AB.CD $$\Rightarrow 2\left( {A{B^2} + B{D^2}} \right) \ge A{B^2} + B{D^2} + 2AB.CD $$= {\left( {AB + CD} \right)^2}.$ Kéo theo \({\left( {AB + CD} \right)^2} \le 2\left( {4{a^2}} \right) = 8{a^2}\)\( \Rightarrow AB + CD \le 2\sqrt 2 a.\) Đẳng thức xảy ra khi và chỉ khi \(AB = CD.\) Xét tam giác \(\Delta ABI,\,\,\Delta DCI\) có \(AB = CD,\) \(\widehat {ABD} = \widehat {ACD}\) (góc nội tiếp cùng chắn cung \(AD),\) \(\widehat {BAC} = \widehat {DCB}\) (góc nội tiếp cùng chắn cung \(BC).\) Do đó \(\Delta ABI = \Delta DCI\left( {g.c.g}. \right)\) Kéo theo \(AI = ID,\,IB = IC.\) Suy ra \(AC = AI + IC = ID + IB = BD.\)
Câu 23 :
Cho tam giác \(ABC\) không cân, nội tiếp đường tròn \(\left( O \right),\,\,BD\) là đường phân giác của góc \(\widehat {ABC}.\) Đường thẳng \(BD\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(E.\) Đường tròn \(\left( {{O_1}} \right)\) đường kính \(DE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Khi đó đường thẳng đối xứng với đường thẳng \(BF\) qua đường thẳng \(BD\) cắt \(AC\) tại \(N\) thì:
Đáp án : A Phương pháp giải :
Chứng minh \(N\) là trung điểm của \(AC\) bằng cách gọi \(M\) là trung diểm của \(AC\) rồi chứng minh \(\widehat {FBE} = \widehat {MBE}\), từ đó suy ra \(BM\) đối xứng với \(BF\) qua \(BE\). Lời giải chi tiết :
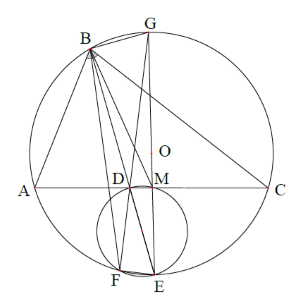 Gọi \(M\) là trung điểm của \(AC.\) Do \(E\) là điểm chính giữa cung \(AC\) nên \(EM \bot AC.\) Do đó \(EM\) đi qua tâm của đường tròn \(\left( O \right).\) Giả sử rằng \(G = DF \cap \left( O \right).\) Do \(\widehat {DFE} = {90^0},\) nên \(\widehat {GFE} = {90^0},\) hay \(GE\) là đường kính của \(\left( O \right).\) Suy ra \(G,M,E\) thẳng hàng. Vì vậy \(\widehat {GBE} = {90^0},\) mà \(\widehat {GMD} = {90^0}.\) Kéo theo tứ giác \(BDMG\) là tứ giác nội tiếp đường tròn đường kính \(GD.\) Vì vậy \(\widehat {MBD} = \widehat {DGM} = \widehat {FGE}\,\,\left( 1 \right)\) (cùng chắn cung \(DM)\) Lại có tứ giác \(BFEG\) là tứ giác nội tiếp nên \(\widehat {FBE} = \widehat {FGE}\,\,\left( 2 \right)\,\) ( cùng chắn cung \(FE\) ). Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(\widehat {MBD} = \widehat {FBE}.\) Do đó \(BF\) và \(BM\) đối xứng nhau qua \(BD.\) Vì vậy \(M \equiv N\) hay \(N\) là trung điểm của \(AC\) nên \(AN = NC.\)
|



















Danh sách bình luận