Trắc nghiệm Bài 6: Cung chứa góc Toán 9Đề bài
Câu 1 :
Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là
Câu 2 :
Với đoạn thẳng \(AB\) và góc \(\alpha \) \(\left( {0^\circ < \alpha < 180^\circ } \right)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat {AMB} = \alpha \) là
Câu 3 :
Cho tam giác \(ABC\) có \(BC\) cố định và góc \(A\) bằng \(50^\circ \). Gọi \(D\) là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm \(D\).
Câu 4 :
Cho các hình thoi $ABCD$ có cạnh $AB$ cố định. Tìm quỹ tích giao điểm $O$ của hai đường chéo của hình thoi đó.
Câu 5 :
Cho nửa đường tròn đường kính \(AB\). Gọi \(M\) là điểm chính giữa của cung \(AB\) . Trên cung \(AM\) lấy điểm \(N\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MB\), trên tia đối của tia \(NB\) lấy điểm \(E\) sao cho \(NA = NE\), trên tia đối của tia \(MB\) lấy điểm \(C\) sao cho \(MC = MA\) . Các điểm nào dưới đây cùng thuộc một đường tròn ?
Câu 6 :
Cho hình vuông \(ABCD\). Trên cạnh \(BC\) lấy điểm \(E\) , trên tia đối của tia \(CD\) lấy điểm \(F\) sao cho \(CE = CF\). Gọi \(M\) là giao điểm của hai đường thẳng \(DE\) và \(BF\). Tìm quỹ tích của điểm \(M\) khi \(E\) di động trên cạnh \(BC\).
Câu 7 :
Cho tam giác đều $ABC$ . Tìm quỹ tích các điểm $M$ nằm trong tam giác đó sao cho \(M{A^2} = M{B^2} + M{C^2}\).
Câu 8 :
Cho tam giác $ABC$ vuông cân tại $A$ . Tìm quỹ tích các điểm $M$ nằm trong tam giác đó sao cho \(2M{A^2} = M{B^2} - M{C^2}\).
Câu 9 :
Cho hình bình hành $ABCD$ , hai đường chéo cắt nhau tại $I$ . Từ $A$ kẻ các đường vuông góc với $BC$ , $CD$ , $DB$ thứ tự tại $H,E,K$ . Xét các khẳng định sau: I. Bốn điểm $A,H,C,E$ nằm trên một đường tròn. II. Bốn điểm $A,K,D,E$ nằm trên một đường tròn. III. Bốn điểm $A,H,K,B$ nằm trên một đường tròn. IV. Bốn điểm $K,I,E,H$ nằm trên một đường tròn. Chọn khẳng định đúng.
Câu 10 :
Cho đường tròn đường kính $AB$ cố định, $M$ là một điểm chạy trên đường tròn. Trên tia đối của tia $MA$ lấy điểm $I$ sao cho $MI = 2MB$. Quỹ tích các điểm $I$ là:
Câu 11 :
Cho tam giác$ABC$ , gọi $I$ là tâm đường tròn nội tiếp tam giác, $P$ là một điểm trong tam giác thỏa mãn \(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB}\). Xét các khẳng định sau: I. $P$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\) II. $I$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\) Kết luận nào sau đây đúng?
Câu 12 :
Cho tam giác $ABC$ cân tại $A,M$ là điểm trên cạnh đáy $BC$. Qua $M$ kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại $D$ và $E$. Gọi $N$ là điểm đối xứng của $M$ qua $DE$. Quỹ tích các điểm $N$ là:
Câu 13 :
Cho đoạn thẳng \(AB = 10cm\), \(M\) là trung điểm của \(AB\). Quỹ tích các điểm \(C\) trong mặt phẳng thỏa mãn tam giác \(ABC\) có \(C{A^2} + C{B^2} = 100\) là:
Câu 14 :
Cho tam giác ABC nội tiếp đường tròn (O,R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau: (I): O nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\). (II): I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\). (III): H trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
Câu 15 :
Cho nửa đường tròn đường kính AB, dây MN có độ dài bằng bán kính R của đường tròn, M thuộc cung AN. Các tia AM và BN cắt nhau ở I, dây AN và BM cắt nhau ở K. Với vị trí nào của dây MN thì diện tích tam giác IAB lớn nhất? Tính diện tích đó theo bán kính R.
Lời giải và đáp án
Câu 1 :
Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là
Đáp án : A Lời giải chi tiết :
Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\).
Câu 2 :
Với đoạn thẳng \(AB\) và góc \(\alpha \) \(\left( {0^\circ < \alpha < 180^\circ } \right)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat {AMB} = \alpha \) là
Đáp án : C Lời giải chi tiết :
Với đoạn thẳng \(AB\) và góc \(\alpha \) \(\left( {0^\circ < \alpha < 180^\circ } \right)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat {AMB} = \alpha \) là hai cung chứa góc \(\alpha \) dựng trên đoạn \(AB\). Hai cung chứa góc \(\alpha \) nói trên là hai cung tròn đối xứng nhau qua \(AB\). Hai điểm \(A,B\) được coi là thuộc quỹ tích.
Câu 3 :
Cho tam giác \(ABC\) có \(BC\) cố định và góc \(A\) bằng \(50^\circ \). Gọi \(D\) là giao điểm của ba đường phân giác trong của tam giác. Tìm quỹ tích điểm \(D\).
Đáp án : D Phương pháp giải :
Sử dụng tính chất tia phân giác để tính góc \(BDC\) từ đó sử dụng quỹ tích cung chứa góc Lời giải chi tiết :
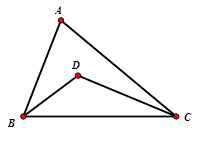 Ta có \(\widehat A = 50^\circ \Rightarrow \widehat B + \widehat C = 130^\circ \) nên \(\widehat {BDC} + \widehat {DBC} = \dfrac{{130^\circ }}{2} = 65^\circ \Rightarrow \widehat {BDC} = 115^\circ \) Quỹ tích của điểm $D$ là hai cung chứa góc \(115^\circ \) dựng trên đoạn $BC$.
Câu 4 :
Cho các hình thoi $ABCD$ có cạnh $AB$ cố định. Tìm quỹ tích giao điểm $O$ của hai đường chéo của hình thoi đó.
Đáp án : B Phương pháp giải :
Sử dụng phương pháp cung chứa góc. Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên $BC$ . Lời giải chi tiết :
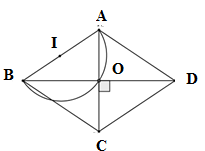 Xét hình thoi $ABCD$ có hai đường chéo $AC$ và $BD$ vuông góc với nhau tại trung điểm của mỗi đường. Suy ra \(AO \bot BO \Rightarrow \) \(\widehat {AOB} = {90^0}\) Ta có \(\widehat {AOB} = {90^0}\) không đổi mà $A,B$ cố định \( \Rightarrow \) Quỹ tích điểm $O$ là nửa đường tròn đường kính $AB$ trừ hai điểm $A$ và $B.$
Câu 5 :
Cho nửa đường tròn đường kính \(AB\). Gọi \(M\) là điểm chính giữa của cung \(AB\) . Trên cung \(AM\) lấy điểm \(N\). Trên tia đối của tia \(MA\) lấy điểm \(D\) sao cho \(MD = MB\), trên tia đối của tia \(NB\) lấy điểm \(E\) sao cho \(NA = NE\), trên tia đối của tia \(MB\) lấy điểm \(C\) sao cho \(MC = MA\) . Các điểm nào dưới đây cùng thuộc một đường tròn ?
Đáp án : C Phương pháp giải :
Chứng minh các đỉnh cùng nhìn một đoạn thẳng dưới một góc cho trước Lời giải chi tiết :
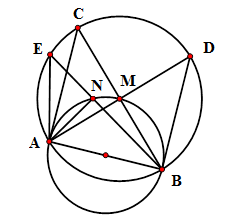 Các tam giác \(\Delta ANE,\,\Delta AMC,\,\Delta BMD\) lần lượt vuông cân tại $N,M,M$ nên \(\widehat {AEB} = \widehat {ADB} = \widehat {ACB} = 45^\circ \) Mà $AB$ cố định nên các điểm $A,B,C,D,E$ cùng thuộc một đường tròn.
Câu 6 :
Cho hình vuông \(ABCD\). Trên cạnh \(BC\) lấy điểm \(E\) , trên tia đối của tia \(CD\) lấy điểm \(F\) sao cho \(CE = CF\). Gọi \(M\) là giao điểm của hai đường thẳng \(DE\) và \(BF\). Tìm quỹ tích của điểm \(M\) khi \(E\) di động trên cạnh \(BC\).
Đáp án : B Phương pháp giải :
Sử dụng : Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\). Lời giải chi tiết :
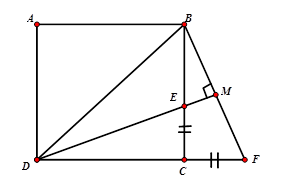 Ta có \(\Delta DEC = \Delta BFC\left( {c - g - c} \right)\) \( \Rightarrow \widehat {EDC} = \widehat {EBM}\) \( \Rightarrow \widehat {EDC} + \widehat {DEC} = \widehat {EBM} + \widehat {BEM} \Rightarrow \widehat {EMB} = 90^\circ \) Hay \(\widehat {BMD} = 90^\circ \) nên $M$ thuộc đườngtròn đường kính$BD$ . Mà \(E \in BC\) nên quỹ tích của điểm $M$ là cung \(BC\) của đường tròn đường kính $BD$ .
Câu 7 :
Cho tam giác đều $ABC$ . Tìm quỹ tích các điểm $M$ nằm trong tam giác đó sao cho \(M{A^2} = M{B^2} + M{C^2}\).
Đáp án : A Phương pháp giải :
Sử dụng phương pháp cung chứa góc. Hai điểm $B, C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên $BC$. Lời giải chi tiết :
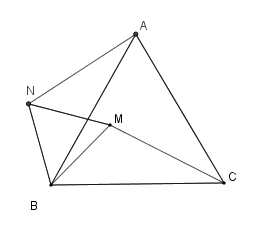 Vẽ tam giác $BMN$ đều ($N$ khác phía $C$ đối với$BM$ ). Xét \(\Delta BNA\) và \(\Delta BMC\) có: \(BN = BM\) (vì tam giác $BMN$ đều) \(BA = BC\) (vì tam giác $ABC$ đều) \(\widehat {NBA} = \widehat {MBC}\) (vì cùng bằng \({60^0\ } - \widehat {ABM}\) ) Suy ra \(\Delta BNA = \Delta BMC(c.g.c)\) nên ta có $NA = MC$. Ta có: \(M{A^2} = M{B^2} + M{C^2} = M{N^2} + N{A^2}\) nên \(\widehat {MNA} = {90^0}\). Suy ra \(\widehat {BNA} = {90^0} + {60^0} = {150^0}\), do đó \(\widehat {BMC} = \widehat {BNA} = {150^0}\). $B,C$ cố định \( \Rightarrow \) Quỹ tích điểm $M$ là hai cung chứa góc \({150^0}\) dựng trên$BC$ , trừ hai điểm $B$ và $C$ .
Câu 8 :
Cho tam giác $ABC$ vuông cân tại $A$ . Tìm quỹ tích các điểm $M$ nằm trong tam giác đó sao cho \(2M{A^2} = M{B^2} - M{C^2}\).
Đáp án : A Phương pháp giải :
Sử dụng phương pháp cung chứa góc. Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên $BC$ . Lời giải chi tiết :
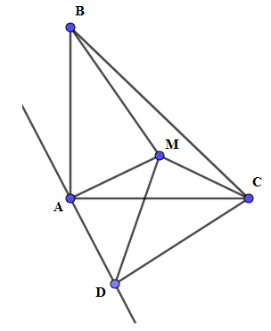 Vẽ tam giác $MAD$ vuông cân tại $A$ ($M$ và $D$ khác phía đối với$AC$ ). Xét \(\Delta BAM\) và \(\Delta CAD\) có: \(AM = AD\) (vì tam giác $MAD$ vuông cân tại$A$ ) \(BA = AC\) (vì tam giác $ABC$ vuông cân tại$A$ ) \(\widehat {MAB} = \widehat {CAD}\) (vì cùng bằng \({90^0} - \widehat {MAC}\) ) Suy ra \(\Delta BAM = \Delta CAD(c - g - c)\) nên ta có $BM = CD$. Ta có: \(2M{A^2} = M{B^2} - M{C^2}\) \( \Rightarrow 2M{A^2} + M{C^2} = M{B^2} \Rightarrow {\left( {MA\sqrt 2 } \right)^2} + M{C^2} = C{D^2} \Rightarrow M{D^2} + M{C^2} = C{D^2}\) nên \(\widehat {DMC} = {90^0}\). Suy ra \(\widehat {AMC} = {135^0}\). Mà $A,C$ cố định \( \Rightarrow \) Quỹ tích điểm M là cung chứa góc \({135^0}\) dựng trên$AC$ , trừ hai điểm $A$ và$C$ .
Câu 9 :
Cho hình bình hành $ABCD$ , hai đường chéo cắt nhau tại $I$ . Từ $A$ kẻ các đường vuông góc với $BC$ , $CD$ , $DB$ thứ tự tại $H,E,K$ . Xét các khẳng định sau: I. Bốn điểm $A,H,C,E$ nằm trên một đường tròn. II. Bốn điểm $A,K,D,E$ nằm trên một đường tròn. III. Bốn điểm $A,H,K,B$ nằm trên một đường tròn. IV. Bốn điểm $K,I,E,H$ nằm trên một đường tròn. Chọn khẳng định đúng.
Đáp án : B Lời giải chi tiết :
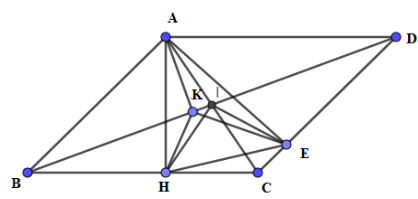 \(AH \bot BC,AE \bot CD \Rightarrow \) bốn điểm $A,H,C,E$ nằm trên đường tròn đường kính$AC$ , $I$ là trung điểm của $AC$ \( \Rightarrow \) $I$ là tâm đường tròn đường kính $AC$ $ \Rightarrow \widehat {HIE} = 2\widehat {HAE} = 2\left( {\widehat {HAC} + \widehat {EAC}} \right)$ \( = 2\left( {{{90}^0} - \widehat {ACB} + {{90}^0} - \widehat {ACE}} \right) = 2\left( {{{180}^0} - \widehat {BCD}} \right)\) Lại có \(AH \bot BC,AK \bot BD,AE \bot CD\) nên bốn đỉnh \(A,K,E,D\) nằm trên đường tròn đường kính \(AD\) và bốn đỉnh \(A;K;H;B\) nằm trên đường tròn đường kính \(AB\) \( \Rightarrow \widehat {EKD} = \widehat {EAD}\) và \(\widehat {BKH} = \widehat {BAH}\) \( \Rightarrow \widehat {HKE} = {180^0} - \widehat {EKD} - \widehat {BKH} = {180^0} - \widehat {EAD} - \widehat {BAH}\\ = {90^0} - \widehat {EAD} + {90^0} - \widehat {BAH} = \widehat {ADC} + \widehat {ABC} = 2\left( {{{180}^0} - \widehat {BCD}} \right)\) Suy ra $K$ và $I$ cùng nhìn đoạn $HE$ dưới một góc \(2\left( {{{180}^0} - \widehat {BCD}} \right)\) Vậy $K,I,E,H$ nằm trên một đường tròn.
Câu 10 :
Cho đường tròn đường kính $AB$ cố định, $M$ là một điểm chạy trên đường tròn. Trên tia đối của tia $MA$ lấy điểm $I$ sao cho $MI = 2MB$. Quỹ tích các điểm $I$ là:
Đáp án : C Phương pháp giải :
Sử dụng phương pháp cung chứa góc. Hai điểm $B,C$ cố định. Quỹ tích các điểm $M$ thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là $2$ cung chứa góc \(\alpha \) dựng trên$BC$ . Lời giải chi tiết :
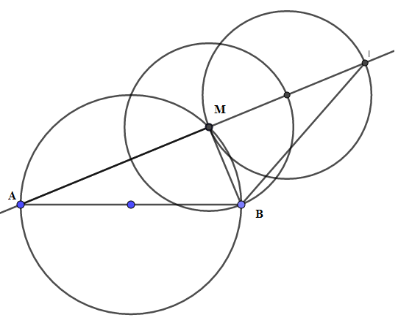 Tam giác $AMB$ vuông tại$M$ , ta có \(\widehat {AMB} = {90^0 }\). Mặt khác ta có: \(\widehat {AMB} + \widehat {IMB} = {180^0 },\) suy ra \(\widehat {IMB} = {90^0 }\) hay tam giác $BMI$ vuông tại $M$ . Trong tam giác vuông $BMI$ ta có \(\tan\widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{1}{2}\) Suy ra \(\widehat {MIB} = {a^0}\) không đổi hay \(\widehat {AIB} = {a^0}\) không đổi. Mà $A,B$ cố định \( \Rightarrow \) Quỹ tích điểm $I$ là $2$ cung chứa góc \({a^0}\) dựng trên $AB$ với \(\tan a = \dfrac{1}{2}.\)
Câu 11 :
Cho tam giác$ABC$ , gọi $I$ là tâm đường tròn nội tiếp tam giác, $P$ là một điểm trong tam giác thỏa mãn \(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB}\). Xét các khẳng định sau: I. $P$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\) II. $I$ nhìn đoạn $BC$ dưới một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\) Kết luận nào sau đây đúng?
Đáp án : B Lời giải chi tiết :
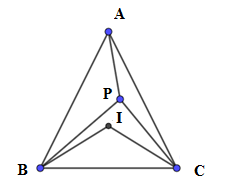 Theo giả thiết ta có:\(\widehat {PBA} + \widehat {PCA} = \widehat {PBC} + \widehat {PCB} \Rightarrow \widehat {PBA} + \widehat {PCA} + \widehat {PBC} + \widehat {PCB} = 2\left( {\widehat {PBC} + \widehat {PCB}} \right)\) \( \Rightarrow 2\left( {\widehat {PBC} + \widehat {PCB}} \right) = \widehat B + \widehat C \Rightarrow 2\left( {{{180}^0} - \widehat {BPC}} \right) = \widehat B + \widehat C = {180^0} - \widehat {BAC}\)\( \Rightarrow \widehat {BPC} = {90^0} + \dfrac{1}{2}\widehat {BAC}\) Mặt khác \(\widehat {BIC} = {180^0} - \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\) \( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC}\) Suy ra $P$ và $I$ luôn nhìn đoạn $BC$ về cùng một phía dưới cùng một góc \({90^0} + \dfrac{1}{2}\widehat {BAC}\).
Câu 12 :
Cho tam giác $ABC$ cân tại $A,M$ là điểm trên cạnh đáy $BC$. Qua $M$ kẻ các đường thẳng song song với hai cạnh bên cắt hai cạnh đó tại $D$ và $E$. Gọi $N$ là điểm đối xứng của $M$ qua $DE$. Quỹ tích các điểm $N$ là:
Đáp án : A Lời giải chi tiết :
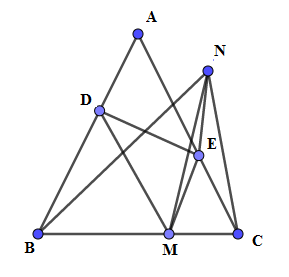 Ta có $MD{\rm{//}}AC,ME{\rm{//}}AB$ \( \Rightarrow \widehat {BDM} = \hat A = \widehat {MEC} \) \(\Rightarrow DB = DM,\;EC = EM.\) $M,N$ đối xứng nhau qua $DE$ \( \Rightarrow DN = DM;\;\;EM = EN.\) \( \Rightarrow \) $D$ là tâm đường tròn ngoại tiếp tam giác $BMN$ \( \Rightarrow \widehat {BNM} = \dfrac{1}{2}\widehat {BDM} = \dfrac{1}{2}\widehat A\) (góc nội tiếp bằng nửa góc ở tâm cùng chắn cung $BM$ ). Tương tự, $E$ là tâm đường tròn ngoại tiếp tam giác $CMN$ . \( \Rightarrow \widehat {MNC} = \dfrac{1}{2}\widehat {MEC} = \dfrac{1}{2}\widehat A\) \( \Rightarrow \widehat {BNC} = \widehat {BNM} + \widehat {MNC} = \widehat A\) Suy ra $N$ nhìn đoạn $BC$ dưới một góc bằng \(\widehat {BAC}\) không đổi. Nên quỹ tích các điểm $N$ là cung chứa góc bằng \(\widehat {BAC}\) dựng trên đoạn $BC$ .
Câu 13 :
Cho đoạn thẳng \(AB = 10cm\), \(M\) là trung điểm của \(AB\). Quỹ tích các điểm \(C\) trong mặt phẳng thỏa mãn tam giác \(ABC\) có \(C{A^2} + C{B^2} = 100\) là:
Đáp án : C Phương pháp giải :
Sử dụng: “Quỹ tích các điểm \(M\) nhìn đoạn thẳng \(AB\) cho trước dưới một góc vuông là đường tròn đường kính \(AB\). » Lời giải chi tiết :
Vì \(C{A^2} + C{B^2} = 100 = A{B^2}\) nên \(\Delta ABC\) là tam giác vuông tại \(C\) hay điểm \(C\) luôn nhìn đoạn \(AB\) một góc \({90^0}\). Do đó quỹ tích các điểm \(C\) là đường tròn đường kính \(AB = 10cm\) hay đường tròn tâm \(M\) bán kính \(5cm\).
Câu 14 :
Cho tam giác ABC nội tiếp đường tròn (O,R), gọi H là trực tâm, I và O là tâm đường tròn nội tiếp và ngoại tiếp tam giác ABC, đồng thời AH bằng bán kính đường tròn ngoại tiếp tam giác ABC. Ta có các nhận xét sau: (I): O nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\). (II): I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\). (III): H trên cung tròn nhìn về một phía của BC dưới góc \({120^\circ }\).
Đáp án : A Phương pháp giải :
Sử dụng tính chất đường trung bình, tính chất hình bình hành và quỹ tích cung chứa góc. Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC. Lời giải chi tiết :
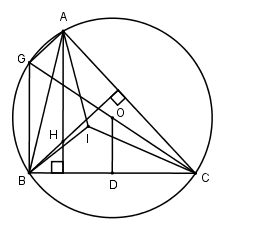 Gọi D là trung điểm của BC. Suy ra \(OD \bot BC\). Kéo dài OC cắt đường tròn tại điểm G ta có : \(\widehat {CBG} = {90^0} \Rightarrow BG \bot BC \Rightarrow BG//AH\) \( \Rightarrow OD = \dfrac{1}{2}BG\) (tính chất đường trung bình). Ta có: \(\widehat {CAG} = {90^0} \Rightarrow AG \bot AC \Leftrightarrow AG//BH \Rightarrow \) AHBG là hình bình hành \( \Rightarrow BG = AH \Rightarrow AH = 2OD\) Theo giả thiết $AH = R \Rightarrow R = OB = 2OD$ Tam giác OBD là tam giác vuông có $OB = 2OD \Rightarrow \widehat {OBD} = {30^0}$ $ \Rightarrow \widehat {BOC} = {120^0} \Rightarrow \widehat {BAC} = {60^0}$ H là trực tâm của tam giác ABC\( \Rightarrow CH \bot AB,BH \bot AC \Rightarrow \widehat {BHC} = {120^\circ }.\) \(\widehat {BIC} = {180^0} - \dfrac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\)\( = {180^0} - \dfrac{1}{2}\left( {{{180}^0} - \widehat {BAC}} \right) = {90^0} + \dfrac{1}{2}\widehat {BAC} = {120^0}\) Ta thấy \(\widehat {BOC} = \widehat {BHC} = \widehat {BIC} = {120^\circ }\)nên ba điểm O, H, I nằm trên cung tròn nhìn về một phía của BC dưới góc \({120^0}\).
Câu 15 :
Cho nửa đường tròn đường kính AB, dây MN có độ dài bằng bán kính R của đường tròn, M thuộc cung AN. Các tia AM và BN cắt nhau ở I, dây AN và BM cắt nhau ở K. Với vị trí nào của dây MN thì diện tích tam giác IAB lớn nhất? Tính diện tích đó theo bán kính R.
Đáp án : D Phương pháp giải :
Sử dụng tính chất hình bình hành, định lý Pytago và quỹ tích cung chứa góc Hai điểm B, C cố định. Quỹ tích các điểm M thỏa mãn \(\widehat {BMC} = \alpha \) không đổi là 2 cung chứa góc \(\alpha \) dựng trên BC. Lời giải chi tiết :
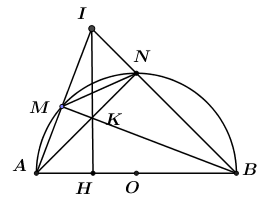 Gọi H là chân đường cao kẻ từ I đến cạnh AB. Khi đó ta có: \({S_{IAB}} = \dfrac{1}{2}IH.AB.\) Ta có AB là đường kính \( \Rightarrow {S_{IAB}}\;\;Max \Leftrightarrow IH\;Max \Leftrightarrow \) H trùng với O. 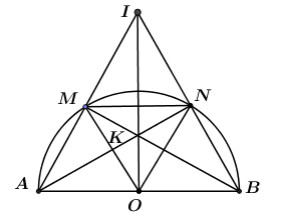 Khi H trùng với O thì OI vừa là đường cao vừa là đường trung tuyến của tam giác \( \Rightarrow \Delta IAB\) cân tại I. Lại có \(\dfrac{{MN}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2} \Rightarrow MN\) là đường trung bình của tam giác \(\Delta ABC\). \( \Rightarrow MN//BC.\) Xét \(\Delta MON\) có \(MO = ON = MN = R \Rightarrow \Delta MON\) là tam giác đều. Tam giác IAB cân tại I có MN là đường trung bình \( \Rightarrow \) M và N lần lượt là trung điểm của AM và AB. Lại có O là trung điểm của AB \( \Rightarrow OM;\;\;ON\) cũng là hai đường trung bình của tam giác IAB. \( \Rightarrow \left\{ \begin{array}{l}ON//IM\\OM//IN\end{array} \right. \Rightarrow \) tứ giác IMON là hình bình hành. Lại có hai đường chéo OI và MN vuông góc với nhau \(\left( {do\;MN//AB;\;\;OI \bot AB} \right).\) \( \Rightarrow IMON\) là hình thoi \( \Rightarrow MI = IN = OM = R \Rightarrow IA = 2IM = 2R.\) Xét tam giác AOI vuông tại O ta có: \(OI = \sqrt {I{A^2} - O{A^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 .\) \( \Rightarrow {S_{IAB}} = \dfrac{1}{2}OI.AB = \dfrac{1}{2}.R\sqrt 3 .2R = {R^2}\sqrt 3 .\)
|



















Danh sách bình luận