Trắc nghiệm Bài 3: Góc nội tiếp Toán 9Đề bài
Câu 1 :
Hình nào dưới đây biểu diễn góc nội tiếp? 
Câu 2 :
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
Câu 3 :
Khẳng định nào sau đây là sai?
Cho đường tròn $(O)$ và điểm $I$ nằm ngoài $(O).$Từ điểm $I$ kẻ hai dây cung $AB$ và $CD$ ( $A$ nằm giữa $I$ và $B,C$ nằm giữa $I$ và $D$). Câu 4
Cặp góc nào sau đây bằng nhau?
Câu 5
Tích $IA.IB$ bằng
Cho tam giác $ABC$ có ba góc nhọn nằm trên đường tròn tâm $(O)$, đường cao $AH$ và đường kính $AM$ Câu 6
Số đo $\widehat {ACM}$ là
Câu 7
Góc $\widehat {OAC}$ bằng
Câu 8
Gọi $N$ là giao điểm của $AH$ với đường tròn $(O)$. Tứ giác $BCMN$ là hình gì ?
Câu 9 :
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
Cho tam giác \(ABC\) nhọn có ba đỉnh thuộc đường tròn \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Vẽ đường kính \(AF\) . Câu 10
Hai đoạn thẳng nào sau đây bằng nhau?
Câu 11
Hệ thức nào dưới đây là đúng?
Câu 12
Gọi \(M\) là trung điểm \(BC\) . Khi đó
Cho \((O)\), đường kính \(AB\), điểm \(D\) thuộc đường tròn. Gọi \(E\) là điểm đối xứng với \(A\) qua \(D.\) Câu 13
Tam giác $ABE$ là tam giác gì?
Câu 14
Gọi \(K\) là giao điểm của \(EB\) với \((O)\). Chọn khẳng định sai?
Câu 15 :
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
Câu 16 :
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
Câu 17 :
Tam giác $ABC$ nằm trên đường tròn $\left( {O;R} \right)$ biết góc $\widehat C = {45^o}$ và $AB = a$. Bán kính đường tròn $\left( O \right)$ là
Lời giải và đáp án
Câu 1 :
Hình nào dưới đây biểu diễn góc nội tiếp? 
Đáp án : B Phương pháp giải :
Sử dụng định nghĩa góc nội tiếp: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Lời giải chi tiết :
Hình \(1\) góc \(\widehat {BOA}\) là góc ở tâm . Hình \(3\) có \(1\) cạnh không phải là dây của đường tròn. Hình \(4\) đỉnh $B$ không nằm trên đường tròn. Hình \(2\) góc \(\widehat {BCA}\) là góc nội tiếp chắn cung \(AB\)
Câu 2 :
Góc nội tiếp nhỏ hơn hoặc bằng \(90^\circ \) có số đo
Đáp án : A Phương pháp giải :
Dựa vào Định lí mối liên hệ giữa góc nội tiếp với cung bị chắn: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. Lời giải chi tiết :
Trong một đường tròn: Góc nội tiếp (nhỏ hơn hoặc bằng $90^\circ $) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
Câu 3 :
Khẳng định nào sau đây là sai?
Đáp án : D Lời giải chi tiết :
Trong một đường tròn: + Các góc nội tiếp bằng nhau chắn các cung bằng nhau. + Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau. + Góc nội tiếp chắn nửa đường tròn là góc vuông. Như vậy hai góc nội tiếp bằng nhau có thể cùng chắn một cung hoặc chắn các cung bằng nhau . Phương án A, B, C đúng và D sai Cho đường tròn $(O)$ và điểm $I$ nằm ngoài $(O).$Từ điểm $I$ kẻ hai dây cung $AB$ và $CD$ ( $A$ nằm giữa $I$ và $B,C$ nằm giữa $I$ và $D$). Câu 4
Cặp góc nào sau đây bằng nhau?
Đáp án : A Lời giải chi tiết :
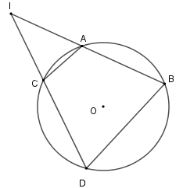 Xét \(\left( O \right)\) có \(\widehat {ACD}\) là góc nội tiếp chắn cung \(AD\) (chứa điểm \(B\) ); \(\widehat {ABD}\) là góc nội tiếp chắn cung $AD$ (chứa điểm \(C\) ) nên \(\widehat {ACD} + \widehat {ABD} = \dfrac{1}{2}.360^\circ = 180^\circ \) Lại có \(\widehat {ACD} + \widehat {ACI} = 180^\circ \) nên \(\widehat {ACI} = \widehat {IBD}\) . Tương tự ta có \(\widehat {IAC} = \widehat {IDB}\) . Câu 5
Tích $IA.IB$ bằng
Đáp án : D Phương pháp giải :
Sử dụng tam giác đồng dạng Lời giải chi tiết :
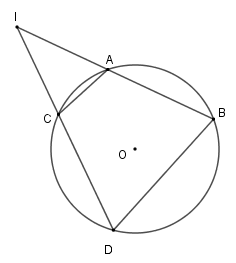 Xét $\Delta IAC$ và \(\Delta IDB\) có \(\widehat I\) chung và \(\widehat {ACI} = \widehat {IBD}\) (câu trước) nên $\Delta IAC\backsim\Delta IDB$ (g-g) \( \Rightarrow \dfrac{{IA}}{{ID}} = \dfrac{{IC}}{{IB}} \Rightarrow IA.IB = IC.ID\) . Cho tam giác $ABC$ có ba góc nhọn nằm trên đường tròn tâm $(O)$, đường cao $AH$ và đường kính $AM$ Câu 6
Số đo $\widehat {ACM}$ là
Đáp án : B Phương pháp giải :
Sử dụng kiến thức: Góc nội tiếp chắn nửa đường tròn là góc vuông. Lời giải chi tiết :
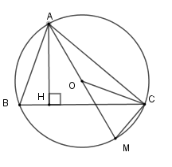 Xét \(\left( O \right)\) có \(\widehat {ACM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACM} = 90^\circ \) . Câu 7
Góc $\widehat {OAC}$ bằng
Đáp án : B Phương pháp giải :
Sử dụng số đo của góc nội tiếp bằng nửa số đo cung bị chắn Lời giải chi tiết :
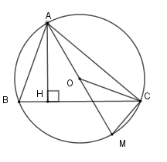 Xét \(\left( O \right)\) có \(\widehat {ABC}\) là góc nội tiếp chắn cung \(AC\) và \(\widehat {CAM}\) là góc nội tiếp chắn cung \(CM\) Nên \(\widehat {ABC} = \dfrac{1}{2}\) sđ \(\overparen{AC}\); \(\widehat {CAM} = \dfrac{1}{2}\) sđ \(\overparen{CM}\) Lại có sđ \(\overparen{AC}+\) sđ \(\overparen{CM}= 180^\circ \) nên \(\widehat {ABC} + \widehat {CAM} = \dfrac{{180^\circ }}{2} = 90^\circ \) Mà \(\widehat {ABC} + \widehat {BAH} = 90^\circ \) nên \(\widehat {BAH} = \widehat {CAM}\) . Câu 8
Gọi $N$ là giao điểm của $AH$ với đường tròn $(O)$. Tứ giác $BCMN$ là hình gì ?
Đáp án : C Phương pháp giải :
+ Sử dụng Góc nội tiếp chắn nửa đường tròn là góc vuông + Dấu hiệu nhận biết hình thang cân: Hình thang có hai cạnh bên bằng nhau là hình thang cân Lời giải chi tiết :
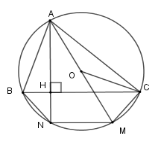 Xét \(\left( O \right)\) có \(\widehat {ANM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ANM} = 90^\circ \) hay \(AN \bot NM\) mà \(BC \bot AN \) nên \(NM{\rm{//}}BC\) Lại có \(\widehat {BAN} = \widehat {CAM}\) (cmt) nên cung $BN = $ cung $CM$ Suy ra \( BN = CM\) Từ đó tứ giác \(BNMC\) có \(NM{\rm{//}}BC\); \(BN = CM\) nên \(BNMC\) là hình thang cân.
Câu 9 :
Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó \(A{B^2}\) bằng
Đáp án : A Phương pháp giải :
Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng Từ đó có hệ thức cần chứng minh. Lời giải chi tiết :
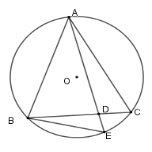 Xét \(\left( O \right)\) có \(\widehat {AEB} = \widehat {ABC}\) (hai góc nội tiếp chắn hai cung bằng nhau \(AB = AC\) ) Xét \(\Delta ABD\) và \(\Delta AEB\) có \(\widehat A\) chung và \(\widehat {AEB} = \widehat {ABC}\) (cmt) nên \(\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD\) Cho tam giác \(ABC\) nhọn có ba đỉnh thuộc đường tròn \(\left( O \right)\). Hai đường cao \(BD\) và \(CE\) cắt nhau tại \(H\). Vẽ đường kính \(AF\) . Câu 10
Hai đoạn thẳng nào sau đây bằng nhau?
Đáp án : C Phương pháp giải :
+ Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông để chứng minh các đường thẳng song song. + Từ đó chứng minh \(BHCF\) là hình bình hành và suy ra các đoạn thẳng bằng nhau Lời giải chi tiết :
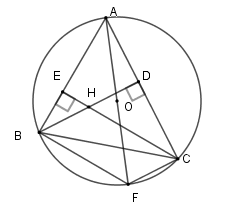 Xét \(\left( O \right)\) có \(\widehat {ACF} = 90^\circ ;\widehat {ABF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) Suy ra \(CF \bot AC;BF \bot AB\) Mà $BD \bot AC;CE \bot AB$ nên \(BD{\rm{//}}CF;CE{\rm{//}}BF\) Suy ra $BHCF$ là hình bình hành Do đó \(BH = CF;BF = CH\) . Câu 11
Hệ thức nào dưới đây là đúng?
Đáp án : A Phương pháp giải :
Sử dụng tam giác đồng dạng Lời giải chi tiết :
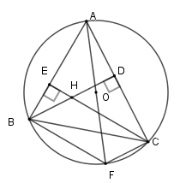 Xét hai tam giác vuông \(\Delta EBH\) và \(\Delta ECA\) có \(\widehat {EBH} = \widehat {ECA}\) (cùng phụ với \(\widehat {BAC}\) ) Nên $\Delta EBH\backsim\Delta ECA\left( {g - g} \right) $ Suy ra $\dfrac{{EB}}{{EC}} = \dfrac{{EH}}{{EA}} $ Dẫn đến $ EB.EA = EC.EH$. Câu 12
Gọi \(M\) là trung điểm \(BC\) . Khi đó
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về đường trung bình của tam giác. Lời giải chi tiết :
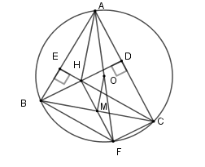 Tứ giác \(BHCF\) là hình bình hành có \(M\) là trung điểm của \(BC\) nên \(M\) cũng là trung điểm của \(HF\) Khi đó \(OM\) là đường trung bình của tam giác \(AHF\) nên \(AH = 2.OM\). Cho \((O)\), đường kính \(AB\), điểm \(D\) thuộc đường tròn. Gọi \(E\) là điểm đối xứng với \(A\) qua \(D.\) Câu 13
Tam giác $ABE$ là tam giác gì?
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc nội tiếp để chứng minh tam giác có đường trung tuyến trùng với đường cao nên nó là tam giác cân. Lời giải chi tiết :
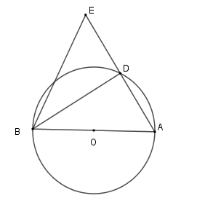 Xét \(\left( O \right)\) có $\widehat {BDA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(BD \bot EA\) mà \(D\) là trung điểm \(EA\) Nên \(\Delta BEA\) có \(BD\) vừa là đường cao vừa là đường trung tuyến nên \(\Delta BAE\) cân tại \(B\) . Câu 14
Gọi \(K\) là giao điểm của \(EB\) với \((O)\). Chọn khẳng định sai?
Đáp án : D Phương pháp giải :
Sử dụng tính chất góc nội tiếp và quan hệ từ vuông góc đến song song Lời giải chi tiết :
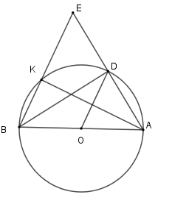 Xét \(\left( O \right)\) có $\widehat {BKA} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) nên \(AK \bot BE\) Mà \(OD\) là đường trung bình của tam giác \(ABE\) nên \(OD{\rm{//}}EB\) từ đó $OD \bot AK.$ Nên A, B, C đúng.
Câu 15 :
Cho tam giác $ABC$ có ba đỉnh thuộc đường tròn tâm $(O)$, đường cao $AH$, đường kính $AD.$ Khi đó tích $AB.AC$ bằng
Đáp án : B Phương pháp giải :
Sử dụng tính chất góc nội tiếp để chứng minh các góc bằng nhau để chứng minh hai tam giác đồng dạng. Lời giải chi tiết :
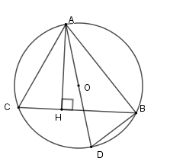 Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) Xét \(\Delta ACH\) và \(\Delta ADB\) có: \(\widehat {ACB} = \widehat {ADB}\) \(\widehat {AHC} = \widehat {ABD} (= 90^\circ) \) Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}} $ Do đó $AH.AD = AC.AB$.
Câu 16 :
Cho tam giác ABC nằm trên đường tròn $(O;R), $đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.
Đáp án : A Phương pháp giải :
Kẻ đường kính \(AD\) Chứng minh \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) Suy ra \( AD = \dfrac{{AB.AC}}{{AH}}\) Lời giải chi tiết :
 Kẻ đường kính \(AD\) Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung \(AB\) ); \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) Nên \(\Delta ACH \backsim \Delta ADB\left( {g - g} \right)\) Suy ra $\dfrac{{AC}}{{AD}} = \dfrac{{AH}}{{AB}}$ Do đó $AH.AD = AC.AB$ Suy ra \(AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{9.12}}{4} = 27\) Do đó \(R = 13,5cm\) .
Câu 17 :
Tam giác $ABC$ nằm trên đường tròn $\left( {O;R} \right)$ biết góc $\widehat C = {45^o}$ và $AB = a$. Bán kính đường tròn $\left( O \right)$ là
Đáp án : C Phương pháp giải :
Sử dụng góc nội tiếp nhỏ hơn \(90^\circ \) có số đo bằng nửa số đo của góc ở tâm chắn cung đó. Sử dụng định lí Pythagore để tính toán. Lời giải chi tiết :
 Xét đường tròn \(\left( O \right)\) có \(\widehat {ACB}\) là góc nội tiếp chắn cung \(AB\) Mà \(\widehat {ACB} = {45^0}\) và \(\widehat {AOB} = {90^0}\) suy ra \(\Delta AOB\) vuông cân tại \(O\). Theo định lí Pythagore ta có $\begin{array}{l}A{O^2} + O{B^2} = A{B^2}\\2A{O^2} = A{B^2}\\AO = \dfrac{{a\sqrt 2 }}{2}\end{array}$ Vậy bán kính đường tròn là \(R = \dfrac{{a\sqrt 2 }}{2}\)
|



















Danh sách bình luận