Trắc nghiệm Bài 6: Tính chất hai tiếp tuyến cắt nhau Toán 9Đề bài
Câu 1 :
Tâm đường tròn nội tiếp của tam giác là
Câu 2 :
Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp?
Câu 3 :
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
Hai tiếp tuyến tại $B$ và $C$ của đường tròn $\left( O \right)$ cắt nhau tại$A$ . Câu 4
Vẽ đường kính $CD$ của $\left( O \right).$ Khi đó
Câu 5
Chọn khẳng định sai ?
Cho nửa đường tròn tâm $O$, đường kính $AB$. Vẽ các tiếp tuyến $Ax,By$ với nữa đường tròn cùng phía đối với $AB$. Từ điểm $M$ trên nửa đường tròn ($M$ khác $A,B$ ) vẽ tiếp tuyến với nửa đường tròn, cắt $Ax$ và $By$ lần lượt tại $C$ và $D$ . Câu 6
Khi đó $MC.MD$ bằng
Câu 7
Cho $OD = BA = 2R$ . Tính $AC$ và $BD$ theo $R.$
Câu 8 :
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.
Câu 9 :
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
Cho tam giác $ABC$ cân tại $A$, $I$ là tâm đường tròn nội tiếp, $K$ là tâm đường tròn bàng tiếp trong góc $A.$ Gọi $O$ là trung điểm của $IK.$ Câu 10
Tâm của đường tròn đi qua bốn điểm $B,I,C,K$ là
Câu 11
Tính bán kính đường tròn $(O)$ biết $AB = AC = 20cm,BC = 24cm.$
Cho đường tròn $\left( O \right)$, bán kính $OA$. Dây $CD$ là đường trung trực của $OA$. Câu 12
Tứ giác $OCAD$ là hình gì?
Câu 13
Kẻ tiếp tuyến với đường tròn tại $C$, tiếp tuyến này cắt đường thẳng $OA$ tại $I$. Biết $OA = R$. Tính $CI$ theo $R$.
Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $\left( O \right)$. Gọi $D$ là trung điểm cạnh $AC$, tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ cắt tia $BD$ tại $E$. Câu 14
Chọn khẳng định đúng.
Câu 15
Tứ giác $ABCE$ là hình gì?
Câu 16 :
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm). Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Câu 17
Chọn câu đúng.
Câu 18
Cho \(FK = 4cm.\) Khi đó:
Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D). Câu 19
Chọn câu đúng nhất.
Câu 20
Tỉ số \(\dfrac{{DE}}{{BE}}\) bằng
Câu 21
Số đo góc \(HEC\) là
Câu 22 :
Hai tiếp tuyến tại hai điểm \(B,C\) của một đường tròn \(\left( O \right)\) cắt nhau tại \(A\) tạo thành \(\widehat {BAC} = {50^0}\). Số đo của góc \(\widehat {BOC}\) chắn cung nhỏ \(BC\) bằng
Câu 23 :
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài tại \(A\). Kẻ tiếp tuyến chung ngoài \(BC,B \in \left( O \right)\) và \(C \in (O')\). Tiếp tuyến chung trong tại \(A\) cắt tiếp tuyến chung ngoài \(BC\) tại \(I\). Tính độ dài \(BC\) biết \(OA = 9cm,O'A = 4cm\).
Câu 24 :
Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn \(\left( {O,3cm} \right)\), \(MA = 4cm\). Độ dài đoạn thẳng AB là:
Lời giải và đáp án
Câu 1 :
Tâm đường tròn nội tiếp của tam giác là
Đáp án : A Lời giải chi tiết :
Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác các góc trong tam giác.
Câu 2 :
Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp?
Đáp án : C Lời giải chi tiết :
Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dàicủa hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác. Với một tam giác có ba đường tròn bàng tiếp.
Câu 3 :
Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Chọn khẳng định sai?
Đáp án : B Lời giải chi tiết :
Nếu hai tiếp tuyến của đường tròn cắt nhau tại một điểm thì: - Điểm đó cách đều hai tiếp điểm. - Tia kẻ từ điểm đó đi qua tâm là tia phân giác của các góc tạo bởi hai tiếp tuyến. - Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm. Hai tiếp tuyến tại $B$ và $C$ của đường tròn $\left( O \right)$ cắt nhau tại$A$ . Câu 4
Vẽ đường kính $CD$ của $\left( O \right).$ Khi đó
Đáp án : A Phương pháp giải :
Sử dụng quan hệ từ vuông góc đến song song Lời giải chi tiết :
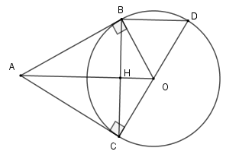 Theo câu trước ta có $AO \bot BC$ (*) Xét tam giác $BCD$ có $DC$ là đường kính của $\left( O \right)$ và $B \in \left( O \right)$ nên $\Delta BDC$ vuông tại $B$ hay $BD \bot BC$ (**) Từ (*) và (**) suy ra $BD{\rm{//}}AO$ Mà $AO$ và $AC$ cắt nhau nên $BD$ và $AC$ không thể song song. Câu 5
Chọn khẳng định sai ?
Đáp án : D Phương pháp giải :
Dựa vào tính chất hai tiếp tuyến cắt nhau. Lời giải chi tiết :
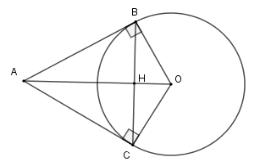 Gọi $H$ là giao của $BC$ với $AO$. Xét $\left( O \right)$ có hai tiếp tuyến tại $B$ và $C$ cắt nhau tại $A$ nên $AB = AC$ (tính chất) Lại có $OB = OC$ nên $AO$ là đường trung trực của đoạn $BC$ hay $AO \bot BC$ tại $H$ là trung điểm của $BC$. Ta chưa kết luận được $H$ có là trung điểm của $AO$ hay không nên đáp án D sai. Cho nửa đường tròn tâm $O$, đường kính $AB$. Vẽ các tiếp tuyến $Ax,By$ với nữa đường tròn cùng phía đối với $AB$. Từ điểm $M$ trên nửa đường tròn ($M$ khác $A,B$ ) vẽ tiếp tuyến với nửa đường tròn, cắt $Ax$ và $By$ lần lượt tại $C$ và $D$ . Câu 6
Khi đó $MC.MD$ bằng
Đáp án : B Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau và hệ thức lượng trong tam giác vuông Lời giải chi tiết :
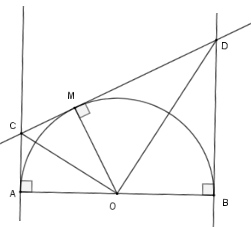 Xét nửa $\left( O \right)$ có $MC$ và $AC$ là hai tiếp tuyến cắt nhau tại $C$ nên $OC$ là phân giác $\widehat {MOA}$ do đó $\widehat {AOC} = \widehat {COM}$ Lại có $MD$ và $BD$ là hai tiếp tuyến cắt nhau tại $D$ nên $OD$ là phân giác $\widehat {MOB}$ do đó $\widehat {DOB} = \widehat {DOM}$ Từ đó $\widehat {AOC} + \widehat {BOD} = \widehat {COM} + \widehat {MOD}$$ = \dfrac{{\widehat {AOC} + \widehat {BOD} + \widehat {COM} + \widehat {MOD}}}{2} = \dfrac{{180^\circ }}{2} = 90^\circ $ Nên $\widehat {COD} = 90^\circ $ hay $\Delta COD$ vuông tại $O$ có $OM$ là đường cao nên $MC.MD = O{M^2}$. Câu 7
Cho $OD = BA = 2R$ . Tính $AC$ và $BD$ theo $R.$
Đáp án : D Phương pháp giải :
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
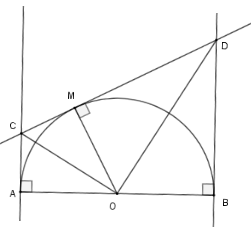 Áp dụng định lý Pytago cho tam giác $BDO$ ta có $BD = \sqrt {O{D^2} - O{B^2}} = \sqrt 3 .R$ Mà $MD = BD;MC = AC$ (tính chất hai tiếp tuyến cắt nhau) nên $MD = \sqrt 3 R$ Theo câu trước ta có $MC.MD = O{M^2} $ $\Rightarrow MC = \dfrac{{O{M^2}}}{{MD}} = \dfrac{{{R^2}}}{{\sqrt 3 .R}} = \dfrac{{R\sqrt 3 }}{3}$ nên $AC = \dfrac{{R\sqrt 3 }}{3}$ Vậy $BD = \sqrt 3 R;AC = \dfrac{{\sqrt 3 R}}{3}.$
Câu 8 :
Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất tam giác cân Lời giải chi tiết :
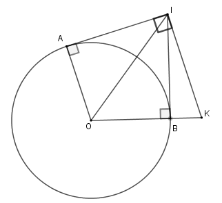 Xét $\left( O \right)$có $IA,IB$ là hai tiếp tuyến cắt nhau tại $I$ nên $\widehat {AOI} = \widehat {KOI}$ Mà $OA{\rm{//}}KI$ (vì cùng vuông góc với $AI$) nên $\widehat {KIO} = \widehat {IOA}$ (hai góc ở vị trí so le trong) Từ đó $\widehat {KOI} = \widehat {KIO}$ suy ra $\Delta KOI$ cân tại $K \Rightarrow KI = KO$.
Câu 9 :
Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
Đáp án : A Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác Lời giải chi tiết :
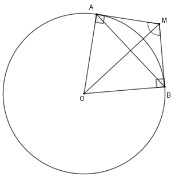 Xét $\left( O \right)$ có $MA = MB$; $\widehat {AMO} = \widehat {BMO}$ (tính chất hai tiếp tuyến cắt nhau) Nên $\widehat {AMO} = 60^\circ $. Xét tam giác vuông $AOM$ có $AM = AO.cot\widehat {AMO} = \dfrac{{R\sqrt 3 }}{3}$ nên $MA = MB = \dfrac{{R\sqrt 3 }}{3}$ Lại có $\widehat {AOB} + \widehat {AMB} = 180^\circ \Rightarrow \widehat {AOB} = 60^\circ $ suy ra $\Delta AOB$ là tam giác đều $ \Rightarrow AB = OB = OA = R$ Chu vi tam giác $MAB$ là $MA + MB + AB = \dfrac{{R\sqrt 3 }}{3} + \dfrac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)$ hay $ R\left( {\dfrac{{3 + 2\sqrt 3 }}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right) \Rightarrow R = 18\,cm$ nên $AB = 18\,cm$. Cho tam giác $ABC$ cân tại $A$, $I$ là tâm đường tròn nội tiếp, $K$ là tâm đường tròn bàng tiếp trong góc $A.$ Gọi $O$ là trung điểm của $IK.$ Câu 10
Tâm của đường tròn đi qua bốn điểm $B,I,C,K$ là
Đáp án : A Phương pháp giải :
Xác định điểm cách đều bốn điểm, điểm đó chính là tâm của đường tròn. Lời giải chi tiết :
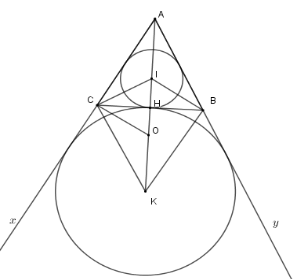 Vì tam giác $ABC$ cân tại $A$ nên $I;K \in $ đường thẳng $AH$ với $\left\{ H \right\} = BC \cap AI$ Ta có $\widehat {HCI} = \dfrac{1}{2}\widehat {HCA};\widehat {KCH} = \dfrac{1}{2}\widehat {xCH}$$ \Rightarrow \widehat {ICK} = \widehat {ICH} + \widehat {HCK} = \dfrac{1}{2}\left( {\widehat {ACH} + \widehat {HCx}} \right) = 90^\circ $ Tương tự ta cũng có $\widehat {IBK} = 90^\circ $ Xét hai tam giác vuông $ICK$ và $IBK$ có $OI = OK = OB = OC = \dfrac{{IK}}{2}$ Nên bốn điểm $B;I;C;K$ nằm trên đường tròn $\left( {O;\dfrac{{IK}}{2}} \right)$. Câu 11
Tính bán kính đường tròn $(O)$ biết $AB = AC = 20cm,BC = 24cm.$
Đáp án : B Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác Lời giải chi tiết :
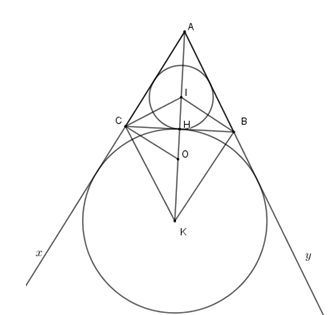 Ta có tam giác $CKI$ vuông nên \(\widehat {CKI} + \widehat {CIO} = 90^\circ \), lại có \(\widehat {CIK} + \widehat {ICH} = 90^\circ \) mà $CI$ là phân giác \(\widehat {ACB}\) nên $\widehat {ACI} =\widehat {CKO} $. Có tam giác $COK$ cân tại $O$ nên \(\widehat {ACI} = \widehat {OCK}\)\( (=\widehat {CKO})\) Nên $\widehat {ICO}+\widehat {ACI}=\widehat {ICO}+\widehat {OCK} = 90 ^\circ $ Suy ra \(\widehat {ACO} = 90^\circ \) $ \Rightarrow OC \bot AC.$ Ta có $HB = HC$ ($AK$ là trung trực của$BC$ ) \( \Rightarrow HB = \dfrac{{BC}}{2} = 12\). Theo Pytago ta có \(AH = \sqrt {A{C^2} - H{C^2}} = 16\) Lại có \(\Delta ACH\backsim\Delta COH\) (hai tam giác vuông có $\widehat {COH} = \widehat {ACH}$ vì cùng phụ với $\widehat {HCO}$) \( \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{HC}}{{CO}}\) \( \Rightarrow CO = \dfrac{{AC.HC}}{{AH}} = 15\) . Cho đường tròn $\left( O \right)$, bán kính $OA$. Dây $CD$ là đường trung trực của $OA$. Câu 12
Tứ giác $OCAD$ là hình gì?
Đáp án : B Phương pháp giải :
Sử dụng liên hệ giữa dây cung và đường kính, dấu hiệu nhận biết các hình đặc biệt Lời giải chi tiết :
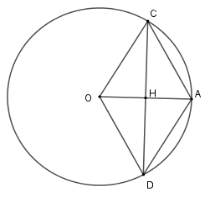 Gọi $H$ là giao của $OA$ và $CD$ Xét $\left( O \right)$ có $OA \bot CD$ tại $H$ nên $H$ là trung điểm của $CD$ Xét tứ giác $OCAD$ có hai đường chéo $OA$ và $CD$ vuông góc với nhau và giao nhau tại trung điểm $H$ mỗi đường nên $OCAD$ là hình thoi. Câu 13
Kẻ tiếp tuyến với đường tròn tại $C$, tiếp tuyến này cắt đường thẳng $OA$ tại $I$. Biết $OA = R$. Tính $CI$ theo $R$.
Đáp án : D Phương pháp giải :
Sử dụng hệ thức giữa cạnh và góc trong tam giác vuông Lời giải chi tiết :
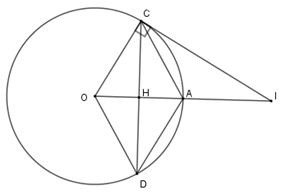 Xét tam giác $COA$ có $OC = OA = R$ và $OC = AC$ (do $OCAD$ là hình thoi) nên $\Delta COA$ là tam giác đều $ \Rightarrow \widehat {COI} = 60^\circ .$ Xét tam giác vuông $OCI$ có $CI = OC.\tan 60^\circ = R\sqrt 3 $. Vậy $CI = R\sqrt 3 $. Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $\left( O \right)$. Gọi $D$ là trung điểm cạnh $AC$, tiếp tuyến của đường tròn $\left( O \right)$ tại $A$ cắt tia $BD$ tại $E$. Câu 14
Chọn khẳng định đúng.
Đáp án : B Phương pháp giải :
Sử dụng quan hệ từ vuông góc đến song song Lời giải chi tiết :
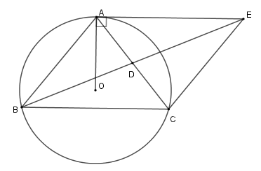 Vì tam giác $ABC$ cân tại $A$ có $O$ là tâm đường tròn ngoại tiếp nên đường thẳng $AO \bot BC$ Lại có $AO \bot AE$ (tính chất tiếp tuyến ) nên $AE{\rm{//}}BC$ Câu 15
Tứ giác $ABCE$ là hình gì?
Đáp án : A Phương pháp giải :
Sử dụng dấu hiệu nhận biết các hình đặc biệt. Lời giải chi tiết :
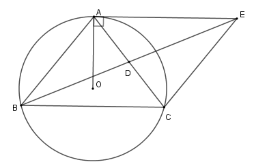 Vì $AE{\rm{//}}BC$ nên $\widehat {EAC} = \widehat {ACB}$ (hai góc ở vị trí so le trong) , lại có $\widehat {ADE} = \widehat {BDC}$ (đối đỉnh) và $AD = DC$ Nên $\Delta ADE = \Delta CDB\left( {g - c - g} \right) $ $\Rightarrow AE = BC$ Tứ giác $AECB$ có $AE = BC;AE{\rm{//}}BC$ nên $AECB$ là hình bình hành.
Câu 16 :
Cho hai đường tròn $\left( O \right);\left( {O'} \right)$ cắt nhau tại $A,B$, trong đó $O' \in \left( O \right)$. Kẻ đường kính $O'OC$ của đường tròn $\left( O \right)$. Chọn khẳng định sai?
Đáp án : D Phương pháp giải :
Sử dụng cách chứng minh một đường thẳng là tiếp tuyến của đường tròn. Lời giải chi tiết :
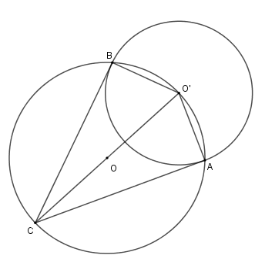 Xét đường tròn $\left( O \right)$ có $O'C$ là đường kính, suy ra $\widehat {CBO'} = \widehat {CAO'} = 90^\circ $ hay $CB \bot O'B$ tại $B$ và $AC \bot AO'$ tại $A$. Do đó $AB,BC$ là hai tiếp tuyến của $\left( {O'} \right)$ nên $AC = CB$ (tính chất hai tiếp tuyến cắt nhau) Nên A, B, C đúng. Cho đường tròn \(\left( {O;R} \right)\). Từ một điểm M nằm ngoài đường tròn kẻ các tiếp tuyến ME, MF đến đường tròn (với E, F là các tiếp điểm). Đoạn OM cắt đường tròn \(\left( {O;R} \right)\) tại I. Kẻ đường kính ED của \(\left( {O;R} \right)\). Hạ FK vuông góc với ED. Gọi P là giao điểm của MD và FK. Câu 17
Chọn câu đúng.
Đáp án : D Phương pháp giải :
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền + Tâm đường tròn nội tiếp tam giác là giao ba đường phân giác + Tâm đường tròn ngoại tiếp tam giác là giao ba đường trung trực Lời giải chi tiết :
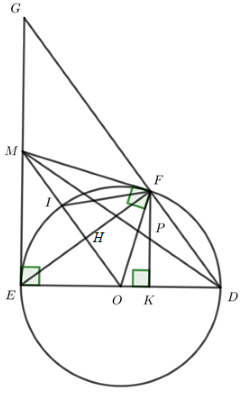 * Vì ME là tiếp tuyến của \(\left( O \right)\) nên ME vuông góc với OE, suy ra tam giác MOE nội tiếp đường tròn đường kính MO (1) Vì MF là tiếp tuyến của \(\left( O \right)\) nên MF vuông góc với OF, suy ra tam giác MOF nội tiếp đường tròn đường kính MO (2) Từ (1) và (2) suy ra M, E, O, F cùng thuộc một đường tròn nên A đúng. * Gọi \(MO \cap EF = \left\{ H \right\}\) Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\) \( \Rightarrow ME = MF\) (tính chất) mà \(OE = OF = R\) (gt) \( \Rightarrow \) MO là đường trung trực của EF \( \Rightarrow MO \bot EF\) \( \Rightarrow \angle IFE + \angle OIF = {90^o}\,\) Vì \(OI = OF = R\) nên tam giác OIF cân tại O \( \Rightarrow \angle OIF = \angle OFI\) mà \(\angle MFI + \angle OFI = {90^o}\,;\,\,\,\angle IFE + \angle OIF = {90^o}\) \( \Rightarrow \angle MFI = \angle IFE\) \( \Rightarrow \) FI là phân giác của \(\angle MFE\) (1) Vì M là giao điểm của 2 tiếp tuyến ME và MF của \(\left( O \right)\) \( \Rightarrow \) MI là phân giác của \(\angle EMF\) (tính chất) (2) Từ (1) và (2) \( \Rightarrow \) I là tâm đường tròn nội tiếp tam giác MEF Câu 18
Cho \(FK = 4cm.\) Khi đó:
Đáp án : A Phương pháp giải :
Kéo dài DF và EM cắt nhau tại G từ đó sử dụng định lý Ta-let để chứng minh. Lời giải chi tiết :
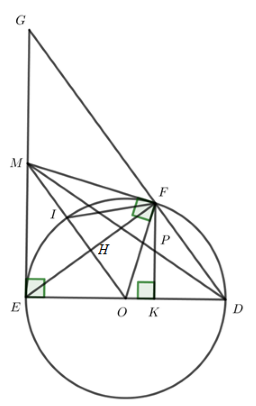 Gọi G là giao điểm của tia DF và tia EM. Ta có \(\angle EFD = {90^o}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow EF \bot DG\) mà \(EF \bot OM\) (cmt) \( \Rightarrow OM//DG\) (từ vuông góc đến song song) Tam giác EDG có \(OE = OD\,\,;\,\,OM//DG\,\, \Rightarrow ME = MG\)(tính chất đường trung bình) Áp dụng định lý Ta-let cho tam giác EDM có \(PK//ME\) (cùng vuông góc với ED) ta được: \(\dfrac{{PK}}{{ME}} = \dfrac{{DP}}{{DM}}\) (3) Áp dụng định lý Ta-let cho tam giác MDG có \(PF//MG\) (cùng vuông góc với ED) ta được: \(\dfrac{{PF}}{{MG}} = \dfrac{{DP}}{{DM}}\) (4) Từ (3) và (4) suy ra \(\dfrac{{PK}}{{ME}} = \dfrac{{PF}}{{MG}}\) mà \(ME = MG\) (cmt) \( \Rightarrow PK = PF\,\, \Rightarrow \) P là trung điểm của FK. Suy ra \(FP = PK = \dfrac{4}{2} = 2cm\) Cho đường tròn \(\left( {O;R} \right)\) và điểm A nằm ngoài \(\left( O \right)\). Từ A kẻ hai tiếp tuyến AB, AC với \(\left( O \right)\) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với \(\left( O \right)\) (E không trùng với D). Câu 19
Chọn câu đúng nhất.
Đáp án : D Phương pháp giải :
+ Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền + Áp dụng tính chất hai tiếp tuyến cắt nhau và tính chất của tam giác cân để chứng minh Lời giải chi tiết :
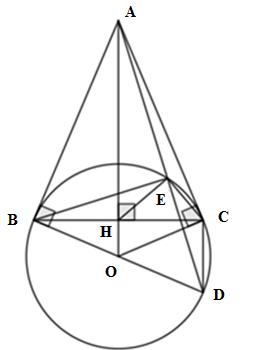 * Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\)\( \Rightarrow \angle OBA = \angle OCA = {90^o}\) \( \Rightarrow \) B, C cùng thuộc đường tròn đường kính OA \( \Rightarrow \) A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai. * Ta có AB, AC là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại A \( \Rightarrow \) \(AB = AC\) và AO là phân giác \(\angle BAC\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow \Delta ABC\) là tam giác cân tại A \( \Rightarrow \) AO vừa là phân giác \(\angle BAC\) vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai. Câu 20
Tỉ số \(\dfrac{{DE}}{{BE}}\) bằng
Đáp án : C Phương pháp giải :
Sử dụng tam giác đồng dạng theo trường hợp góc – góc Chứng minh \(\Delta BED\) và \(\Delta ABD\) là hai tam giác đồng dạng từ đó suy ra hệ thức đúng. Lời giải chi tiết :
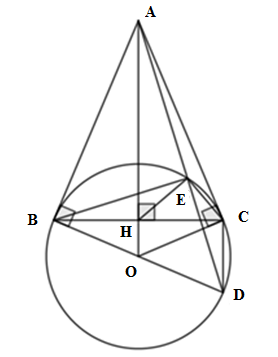 Ta có D đối xứng với B qua O \( \Rightarrow \) BD là đường kính của \(\left( O \right)\) mà \(E \in \left( O \right)\) \( \Rightarrow \) \(\angle BED = {90^o}\) Xét \(\Delta BED\) và \(\Delta ABD\) có: \(\angle BED = \angle ABD = {90^o}\), \(\angle D\) chung \( \Rightarrow \Delta BED \backsim \Delta ABD\left( {g - g} \right) \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}.\) Câu 21
Số đo góc \(HEC\) là
Đáp án : D Phương pháp giải :
Sử dụng các cặp tam giác đồng dạng để tính số đo góc. + Chứng minh \(\Delta BCD \backsim \Delta AHB\) + Chứng minh \(\Delta BHE \backsim \Delta DCE\) Lời giải chi tiết :
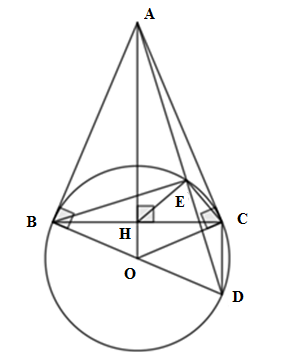 \(\angle BCD = {90^o}\) (góc nội tiếp chắn nửa đường tròn) \(\angle AHB = {90^o}\) (AO là trung trực của BC) Xét \(\Delta BCD\) và \(\Delta AHB\) có: \(\angle BCD = \angle AHB = {90^o},\;\angle BDC = \angle ABH\) (BA là tiếp tuyến của \(\left( O \right)\) tại B) \( \Rightarrow \Delta BCD \backsim \Delta AHB\;\left( {g - g} \right) \)\(\Rightarrow \dfrac{{BD}}{{BA}} = \dfrac{{CD}}{{BH}}\) mà theo câu trước \(\dfrac{{DE}}{{BE}} = \dfrac{{BD}}{{BA}}\) \( \Rightarrow \dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\) Xét \(\Delta BHE\) và \(\Delta DCE\) có \(\dfrac{{DE}}{{BE}} = \dfrac{{CD}}{{BH}}\)\( \Rightarrow \Delta BHE \backsim \Delta DCE \Rightarrow \angle BEH = \angle DEC\) (2 góc tương ứng) \( \Rightarrow \angle BEH + \angle HED = \angle DEC + \angle HED \)\(\Rightarrow \angle BED = \angle HEC\) Mà \(\angle BED = {90^o}\) (chứng minh trên) Vậy \(\angle HEC = {90^o}\)
Câu 22 :
Hai tiếp tuyến tại hai điểm \(B,C\) của một đường tròn \(\left( O \right)\) cắt nhau tại \(A\) tạo thành \(\widehat {BAC} = {50^0}\). Số đo của góc \(\widehat {BOC}\) chắn cung nhỏ \(BC\) bằng
Đáp án : C Phương pháp giải :
Tính chất hai tiếp tuyến cắt nhau. Lời giải chi tiết :
Vì hai tiếp tuyến của đường tròn \(\left( O \right)\) cắt nhau tại \(A\) nên \(\widehat {ACO} = \widehat {ABO} = {90^0} \Rightarrow \widehat {CAB} + \widehat {COB} = {360^0} - {180^0} = {180^0}\) Mà \(\widehat {CAB} = {50^0}\) nên \(\widehat {COB} = {180^0} - {50^0} = {130^0}\)
Câu 23 :
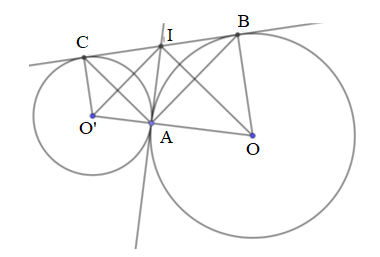
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài tại \(A\). Kẻ tiếp tuyến chung ngoài \(BC,B \in \left( O \right)\) và \(C \in (O')\). Tiếp tuyến chung trong tại \(A\) cắt tiếp tuyến chung ngoài \(BC\) tại \(I\). Tính độ dài \(BC\) biết \(OA = 9cm,O'A = 4cm\).
Đáp án : A Phương pháp giải :
Sử dụng tính chất hai tiếp tuyến cắt nhau Sử dụng công thức lượng giác Lời giải chi tiết :
Ta có \(IO\) là tia phân giác của \(\widehat {BIA}\) \(IO'\) là tia phân giác của \(\widehat {CIA}\) Mà \(\widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}\) Tam giác \(OIO'\) vuông tại \(I\) có \(IA\) là đường cao nên \(I{A^2} = AO.AO' = 9.4 = 36 \Rightarrow IA = 6cm\). \( \Rightarrow IA = IB = IC = 6cm\) (tính chất hai tiếp tuyến cắt nhau) Vậy \(BC = 2IA = 2.6 = 12\left( {cm} \right)\).
Câu 24 :
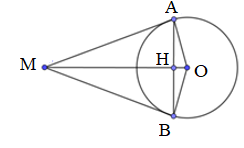
Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn \(\left( {O,3cm} \right)\), \(MA = 4cm\). Độ dài đoạn thẳng AB là:
Đáp án : A Phương pháp giải :
Áp dụng hệ thức lượng trong tam giác vuông. Lời giải chi tiết :
Vì MA và MB là tiếp tuyến nên \(MA = MB\) nên M thuộc trung trực của AB Mà \(OA = OB\) do cùng là bán kính nên O thuộc trung trực của AB Suy ra OM là trung trực của AB. Gọi H là giao điểm của MO và AB, ta có \(AH = BH\) Xét tam giác vuông AMO vuông tại A (do MA là tiếp tuyến) có AH là đường cao \( \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{M^2}}} + \dfrac{1}{{A{O^2}}} \Rightarrow AH = \sqrt {\dfrac{{A{M^2}.A{O^2}}}{{A{M^2} + A{O^2}}}} = \sqrt {\dfrac{{{4^2}{{.3}^2}}}{{{4^2} + {3^2}}}} = 2,4\) Suy ra \(AB = 2AH = 2.2,4 = 4,8\).
|














_co_tiep_tuyen_AB_AC.png)





Danh sách bình luận