Trắc nghiệm Bài 10: Diện tích hình tròn, quạt tròn Toán 9Đề bài
Câu 1 :
Một hình tròn có diện tích \(S = 144\pi \,\left( {c{m^2}} \right)\) . Bán kính của hình tròn đó là:
Câu 2 :
Diện tích hình tròn bán kính \(R = 10\,cm\) là
Câu 3 :
Cho đường tròn $\left( {O,10\,cm} \right)$, đường kính $AB.$. Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {45^0}\). Tính diện tích hình quạt $AOM$ .
Câu 4 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ \(4\sqrt 3 \) $cm$ . Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình viên phân$AC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
Câu 5 :
Cho hình vuông có cạnh là $5\,cm$ nội tiếp đường tròn $\left( O \right)$. Hãy tính diện tích hình tròn $\left( O \right)$.
Câu 6 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 2\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ .
Câu 7 :
Một hình quạt có chu vi bằng \(28\,(cm)\) và diện tích bằng \(49\,(c{m^2})\). Bán kính của hình quạt bằng?
Câu 8 :
Cho đường tròn $\left( {O;R} \right)$ và một điểm $M$ sao cho $OM = 2R$. Từ $M$ vẽ các tiếp tuyến $MA,MB$ với đường tròn $(A,B$ là các tiếp điểm ). Tính diện tích giới hạn bởi hai tiếp tuyến $AM,MB$ và cung nhỏ $AB.$
Câu 9 :
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
Lời giải và đáp án
Câu 1 :
Một hình tròn có diện tích \(S = 144\pi \,\left( {c{m^2}} \right)\) . Bán kính của hình tròn đó là:
Đáp án : C Phương pháp giải :
Sử dụng công thức: Diện tích $S$ của một hình tròn bán kính $R$ là \(S = \pi {R^2}.\) Lời giải chi tiết :
Diện tích \(S = \pi {R^2} = 144\pi \Leftrightarrow {R^2} = 144 \Leftrightarrow R = 12\,\left( {cm} \right)\).
Câu 2 :
Diện tích hình tròn bán kính \(R = 10\,cm\) là
Đáp án : A Phương pháp giải :
Sử dụng công thức: Diện tích $S$ của một hình tròn bán kính $R$ là \(S = \pi {R^2}.\) Lời giải chi tiết :
Diện tích \(S = \pi {R^2} = \pi {.10^2} = 100\pi \,\left( {c{m^2}} \right)\).
Câu 3 :
Cho đường tròn $\left( {O,10\,cm} \right)$, đường kính $AB.$. Điểm \(M \in (O)\) sao cho \(\widehat {BAM} = {45^0}\). Tính diện tích hình quạt $AOM$ .
Đáp án : B Phương pháp giải :
Sử dụng công thức tính diện tích hình quạt tròn có bán kính $R$ với góc ở tâm \({n^0}\): \({S_q} = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{lR}}{2}.\) Lời giải chi tiết :
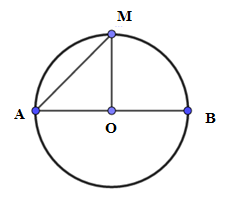 Xét đường tròn $\left( O \right)$ có: \(OA = OM\) và \(\widehat {MAO} = {45^0}\) nên \(\Delta AOM\) là tam giác vuông cân. Suy ra \(\widehat {MOA} = {90^0}.\) Vậy diện tích hình quạt $AOM$ là \(S = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{\pi {{.10}^2}.90}}{{360}} = 25\pi (c{m^2})\)
Câu 4 :
Cho đường tròn $\left( O \right)$ đường kính $AB = $ \(4\sqrt 3 \) $cm$ . Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình viên phân$AC$ . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
Đáp án : B Phương pháp giải :
Áp dụng công thức tính diện tích hình viên phân. \({S_{vp\,AC}} = {S_{qAOC}} - {S_\Delta }_{AOC}\) Lời giải chi tiết :
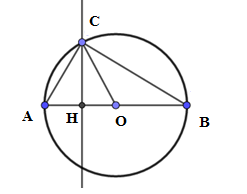 Xét đường tròn $(O)$ có: \(\widehat {ABC}\) và \(\widehat {AOC}\) là góc nội tiếp và góc ở tâm cùng chắn cung$AC$ \( \Rightarrow \widehat {AOC} = 2.\widehat {ABC} = {2.30^0} = {60^0}\)\( \Rightarrow {S_{qAOC}} = \dfrac{{\pi {R^2}.60}}{{360}} = \dfrac{{\pi {R^2}}}{6}\) Xét \(\Delta AOC\) có \(\widehat {AOC} = {60^\circ }\) và $OA=OC=R$ nên tam giác $AOC$ đều cạnh bằng $R$ . Gọi $CH$ là đường cao của tam giác $AOC$ , ta có: \(CH = CO.\sin {60^0} = \dfrac{{\sqrt 3 }}{2}.R \Rightarrow {S_{AOC}} = \dfrac{1}{2}CH.OA = \dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2}.R.R = \dfrac{{\sqrt 3 }}{4}.{R^2}.\) Diện tích hình viên phân $AC$ là: \({S_{qAOC}} - {S_{AOC}} = \dfrac{{\pi {R^2}}}{6} - \dfrac{{\sqrt 3 }}{4}.{R^2} = \left( {\dfrac{\pi }{6} - \dfrac{{\sqrt 3 }}{4}} \right).{R^2} \) \(= \left( {\dfrac{{2\pi - 3\sqrt 3 }}{{12}}} \right).{\left( {2\sqrt 3 } \right)^2} \) \(= 2\pi - 3\sqrt 3 \, cm^2.\)
Câu 5 :
Cho hình vuông có cạnh là $5\,cm$ nội tiếp đường tròn $\left( O \right)$. Hãy tính diện tích hình tròn $\left( O \right)$.
Đáp án : D Phương pháp giải :
Áp dụng công thức tính diện tích hình tròn \(S = \pi {R^2}.\) Lời giải chi tiết :
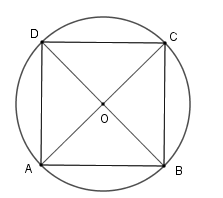 Gọi hình vuông \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) khi đó $OA = OB = OC = OD = R \Rightarrow O$ là giao điểm của \(AC\) và \(BD\) \( \Rightarrow R = \dfrac{{AC}}{2}.\) Xét tam giác vuông \(ABC\) ta có \(A{C^2} = A{B^2} + B{C^2} = {5^2} + {5^2} = 50 \Rightarrow AC = 5\sqrt 2 \) \( \Rightarrow R = \dfrac{{5\sqrt 2 }}{2}\) Diện tích hình tròn \(\left( O \right)\) là $S = \pi {R^2} = \dfrac{{25\pi }}{2}\,\left( {c{m^2}} \right).$
Câu 6 :
Cho đường tròn $\left( O \right)$ đường kính \(AB = 2\sqrt 2 \;cm\). Điểm \(C \in (O)\) sao cho \(\widehat {ABC} = {30^0}\). Tính diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ .
Đáp án : A Phương pháp giải :
Diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ là: \(S = \dfrac{1}{2}{S_{(O)}} - {S_{ABC}}\) Lời giải chi tiết :
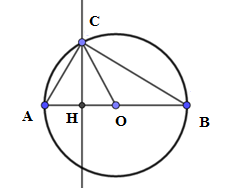 Diện tích hình tròn $\left( O \right)$ là: \({S_{(O)}} = \pi {R^2}\) Ta có góc \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACB} = {90^0}\)\( \Rightarrow \widehat {BAC} = {90^0} - \widehat {CBA} = {90^0} - {30^0} = {60^0}.\) Tam giác $AOC$ có \(\widehat {CAO} = {60^\circ }\) và $OA = OC = R$ nên tam giác $AOC$ đều cạnh bằng $R$ . Giả sử $CH$ là đường cao của tam giác $ABC$ , ta có: \(CH = CO.\sin {60^0} = \dfrac{{\sqrt 3 }}{2}.R \Rightarrow {S_{ABC}} = \dfrac{1}{2}CH.AB\) $= \dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2}R.2R$ \(= \dfrac{{\sqrt 3 }}{2}{R^2}.\) Diện tích hình giới hạn bởi đường tròn $\left( O \right)$ và $AC,BC$ là: $\dfrac{1}{2}{S_{(O)}} - {S_{ABC}} = \dfrac{1}{2}\pi {R^2} - \dfrac{{\sqrt 3 }}{2}{R^2} = \dfrac{1}{2}\left( {\pi - \sqrt 3 } \right){R^2} = \dfrac{1}{2}\left( {\pi - \sqrt 3 } \right){\left( {\sqrt 2 } \right)^2} = \pi - \sqrt 3 .$
Câu 7 :
Một hình quạt có chu vi bằng \(28\,(cm)\) và diện tích bằng \(49\,(c{m^2})\). Bán kính của hình quạt bằng?
Đáp án : C Phương pháp giải :
Sử dụng công thức tính diện tích hình quạt tròn có bán kính $R$ với góc ở tâm \({n^0}\): \(Sq = \dfrac{{\pi {R^2}n}}{{360}} = \dfrac{{lR}}{2}.\) Sử dụng công thức tính chu vi hình quạt \(C = l + 2R\) với $l$ là độ dài cung có số đo $n$ độ. Lời giải chi tiết :
Ta có \(\left\{ \begin{array}{l}\dfrac{{lR}}{2} = 49\\l + 2R = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}lR = 98\\l + 2R = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}l.2R = 196\\l + 2R = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2R = 14\\l = 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}R = 7\\l = 14\end{array} \right.\) . Vậy \(R = 7(cm)\)
Câu 8 :
Cho đường tròn $\left( {O;R} \right)$ và một điểm $M$ sao cho $OM = 2R$. Từ $M$ vẽ các tiếp tuyến $MA,MB$ với đường tròn $(A,B$ là các tiếp điểm ). Tính diện tích giới hạn bởi hai tiếp tuyến $AM,MB$ và cung nhỏ $AB.$
Đáp án : D Phương pháp giải :
Diện tích hình giới hạn bởi cung nhỏ $AB$ và $AM,MB$ là: \(S = {S_{OAMB}} - {S_{q\,AB}}\) Lời giải chi tiết :
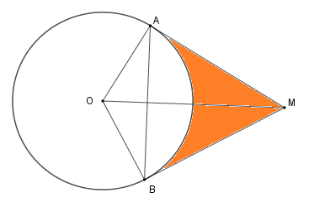 Xét \(\Delta OAM\) có \(AM = \sqrt {O{M^2} - O{A^2}} = R\sqrt 3 \Rightarrow {S_{OAM}} = \dfrac{{OA.AB}}{2} = \dfrac{{{R^2}\sqrt 3 }}{2}\) Mà \(\Delta OAM = \Delta OBM\left( {c - c - c} \right) \Rightarrow {S_{OAMB}} = 2{S_{OAM}} = \sqrt 3 {R^2}\) Xét \(\Delta OAM\) có \(\cos \widehat {AOM} = \dfrac{{OA}}{{OM}} = \dfrac{1}{2} \) \(\Rightarrow \widehat {AOM} = 60^\circ \Rightarrow \widehat {AOB} = 120^\circ \) Diện tích quạt tròn \({S_{q\,AB}} = \dfrac{{\pi {R^2}.120}}{{360}} = \dfrac{{\pi {R^2}}}{3}\) Diện tích giới hạn bởi hai tiếp tuyến $AM,MB$ và cung nhỏ $AB$ là \(S = {S_{OAMB}} - {S_{q\,AB}} = \sqrt 3 {R^2} - \dfrac{{\pi {R^2}}}{3} = {R^2}\left( {\sqrt 3 - \dfrac{\pi }{3}} \right).\)
Câu 9 :
Cho tam giác đều \(ABC\) nội tiếp đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \). Diện tích của tam giác đều \(ABC\) là:
Đáp án : A Phương pháp giải :
+ Áp dụng công thức tính chu vi hình tròn + Tính chất của tam giác cân + Sử dụng định lý Pitago + Sử dụng công thức tính diện tích tam giác Lời giải chi tiết :
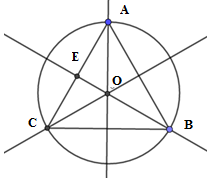 Gọi \(R\) là bán kính của đường tròn \(\left( O \right)\). Độ dài của các cung \(AB,BC,CA\) đều bằng \(4\pi \) nên ta có \(C = 2\pi R = 4\pi + 4\pi + 4\pi = 12\pi \), suy ra \(R = 6\) hay \(OA = OB = OC = 6\) Ta cũng có \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) suy ra \(\Delta AOB = \Delta AOC = \Delta BOC = \dfrac{1}{3}\Delta ABC\) Xét tam giác \(AOC\) có: \(\left\{ \begin{array}{l}\widehat {OAC} = \widehat {OCA} = {30^0}\\\widehat {COA} = {120^0}\end{array} \right.\) Kẻ đường cao$OE$ , ta có đồng thời là đường trung tuyến, phân giác của góc \(\widehat {COA}\) . Ta có \(\widehat {AOE} = \widehat {COE} = \dfrac{1}{2}\widehat {AOC}\) Xét tam giác $COE$ có: \(\left\{ \begin{array}{l}\widehat {ECO} = {30^0}\\\widehat {CEO} = {90^0}\end{array} \right. \Rightarrow OE = \dfrac{1}{2}CO = \dfrac{R}{2}\) Áp dụng định lý Pytago ta có: \(CE = \sqrt {O{C^2} - O{E^2}} = \sqrt {{R^2} - {{\left( {\dfrac{R}{2}} \right)}^2}} = \dfrac{{\sqrt 3 }}{2}R\) Vậy \({S_{COE}} = \dfrac{1}{2}OE.CE = \dfrac{1}{2}.\dfrac{R}{2}.\dfrac{{\sqrt 3 R}}{2} = \dfrac{{\sqrt 3 {R^2}}}{8}\) Suy ra \({S_{COA}} = 2{S_{COE}} = \dfrac{{\sqrt 3 {R^2}}}{4}\) và \({S_{ABC}} = 3{S_{COA}} = \dfrac{{3\sqrt 3 {R^2}}}{4} = \dfrac{{3\sqrt 3 {R^2}}}{4} = 27\sqrt 3 \,\ cm^2 .\)
|



















Danh sách bình luận