Trắc nghiệm Bài tập ôn tập chương 7 Toán 9Đề bài
Câu 1 :
Số đo cung lớn \(BnC\) trong hình bên là: 
Câu 2 :
Cho hình vẽ ở bên. Khi đó mệnh đề đúng là: 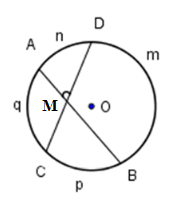
Câu 3 :
Cho bốn điểm A, B, C, D thuộc đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
Câu 4 :
Cho hình vẽ bên. Mệnh đề nào sau đây là sai. 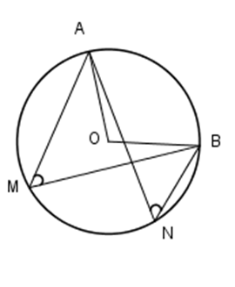
Câu 5 :
Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$ 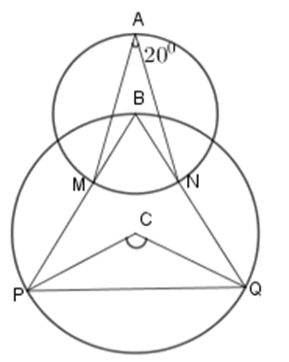 Khi đó \(\widehat {PCQ} = ?\)
Câu 6 :
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\) 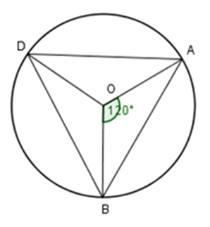 Khi đó \(\Delta ABD\) là:
Câu 7 :
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) cắt nhau tại \(A\) và \(B.\) Vẽ cát tuyến \(CAD\) vuông góc với \(AB\left( {C \in \left( O \right),D \in \left( {O'} \right)} \right)\) . Tia \(CB\) cắt \(\left( {O'} \right)\) tại \(E,\) tia \(DB\) cắt \(\left( O \right)\) tại \(F.\) Khi đó
Câu 8 :
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
Câu 9 :
Cho hình vẽ dưới đây. 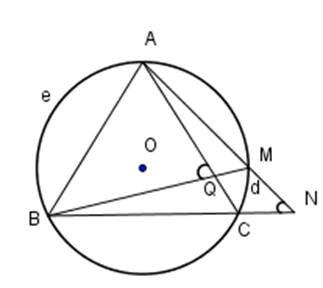 Khi đó mệnh đề đúng là:
Câu 10 :
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
Câu 11 :
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng AP cắt RQ tại S. Khi đó:
Câu 12 :
Cho tam giác nhọn \(ABC\,\,\left( {AB > BC} \right)\) nội tiếp đường tròn \(\left( O \right).\) \(D\) là điểm chính giữa cung \(AC.\) Giả sử \(\{E\} = AB \cap CD,\,\,\{F\} = AD \cap BC.\) Khi đó :
Câu 13 :
Cho hình vẽ, biết số đo cung \(BmD\) là \({120^0}.\) Khi đó 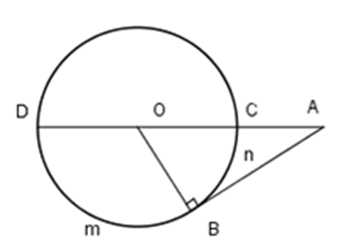
Câu 14 :
Cho đường tròn tâm \(O,\) đường kính \(AB.\) Lấy điểm \(P\) khác \(A\) và \(B\) trên đường tròn sao cho \(\widehat {BAP} = {30^0}.\) Gọi \(T\) là giao điểm của \(AP\) với tiếp tuyến tại \(B\) của đường tròn. Khi đó ta có \(\widehat {PBT} = ?\)
Câu 15 :
Cho hình vẽ ở bên. Biết \( \widehat {BAx}=20^0\). 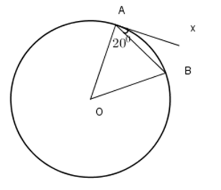 Hãy tính số đo của cung bị chắn \(AB.\)
Câu 16 :
Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai cát tuyến \(ABC\) và \(ADE\) với đường tròn đó (\(B\) nằm giữa \(A\) và \(C,\)\(D\) nằm giữa \(A\) và \(E\)). Kẻ dây \(BF//DE.\) Khi đó kết luận đúng là:
Câu 17 :
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\) .PNG) Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
Câu 18 :
Cho điểm \(C\) thuộc nửa đường tròn \(\left( O \right)\) đường kính \(AB.\) Từ điểm \(D\) thuộc đọan \(AO\) kẻ đường thẳng vuông góc với \(AO\) cắt \(AC\) và \(BC\) lần lượt lại \(E\) và \(F.\) Tiếp tuyến tại \(C\) với nửa đường tròn cắt $EF$ tại \(M\) và cắt \(AB\) tại \(N.\) Khi đó 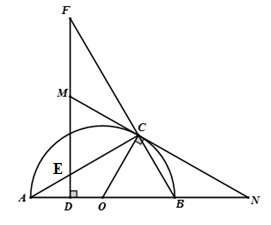
Câu 19 :
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(BC = R.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B,C\) cắt nhau tại \(A.\) Gọi \(M\) là giao điểm của \(AO\) và \(BC.\) Khi đó tam giác \(AMB\) là:
Câu 20 :
Cho hình vẽ. Khi đó đáp án đúng là 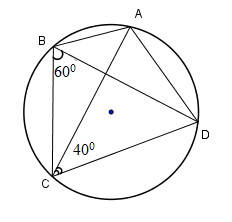
Câu 21 :
Tia phân giác góc \(\widehat {BAD}\) của hình bình hành \(ABCD\) cắt các đường thẳng \(BC\) và \(DC\) lần lượt tại hai điểm \(M\) và \(N.\) Dựng ra phía ngoài hình bình hành \(ABCD\) tam giác \(MCO\) cân tại $O$ với \(\widehat {MOC} = \widehat {BAD}\). Khi đó:
Câu 22 :
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right),\) các đường cao\(AD,\,BE,\,CF\,\left( {D \in BC,\,E \in AC,\,F \in AB} \right)\) cắt nhau tại \(H\). Khi đó ta có
Câu 23 :
Cho nửa đường tròn tâm \(O,\) đường kính \(AB = 2R.\) Đường thẳng qua \(O\) và vuông góc \(AB\) cắt cung \(AB\) tại \(C.\) Gọi \(E\) là trung điểm \(BC.\,AE\) cắt nửa đường tròn \(O\) tại \(F.\) Đường thẳng qua \(C\) và vuông góc $AF$ tại \(G\) cắt \(AB\) tại $H.$ Khi đó góc \(\widehat {OGH}\) có số đo là:
Câu 24 :
Cho hình vuông \(ABCD\) có cạnh \(2R.\) 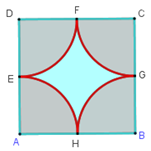 Diện tích \(S\) phần màu xanh trong hình vuông \(ABCD\) là
Cho đường tròn \(\left( {O;R} \right),\) đường kính \(AB\) cố định, đường kính \(CD\) thay đổi \(\left( {CD \ne AB} \right).\) Các tia \(BC,\,BD\) cắt tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) lần lượt tại \(E,\,F.\) Câu 25
Tứ giác \(DCEF\) là
Câu 26
Khi \(CD\) thay đổi. Giá trị nhỏ nhất của \(EF\) theo \(R\) là:
Cho \(BC\) là một dây cung của đường tròn \(\left( {O;R} \right),\,\,\left( {BC \ne 2R} \right).\) Điểm \(A\) di động trên cung lớn \(BC\) sao cho \(O\) luôn nằm trong tam giác \(ABC.\) Các đường cao \(AD,\,BE,\,CF\) của tam giác \(ABC\) đồng quy tại \(H.\) Câu 27
Chọn kết luận sai:
Câu 28
Kẻ đường kính \(AK\) của đường tròn \(\left( {O;R} \right).\) Khi đó \(BHCK\) là:
Câu 29 :
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
Lời giải và đáp án
Câu 1 :
Số đo cung lớn \(BnC\) trong hình bên là: 
Đáp án : A Phương pháp giải :
Số đo cung lớn bằng \(360^\circ - \) số đo cung nhỏ Lời giải chi tiết :
Ta có tổng số đo cung nhỏ \(BmC\) và số đo cung lớn \(BnC\) là \({360^0}.\) Mặt khác số đo cung nhỏ \(BmC = {80^0}.\) Từ đó ta suy ra số đo cung lớn \(BnC\) là: \({360^0} - {80^0} = {280^0}.\)
Câu 2 :
Cho hình vẽ ở bên. Khi đó mệnh đề đúng là: 
Đáp án : A Phương pháp giải :
Tính chất góc có đỉnh nằm trong đường tròn: Số đo góc có đỉnh nằm trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn. Lời giải chi tiết :
Góc \(\widehat {AMD}\) là góc có đỉnh bên trong đường tròn chắn cung \(AD\) và cung \(BC\) nên ta có \(\widehat {AMD} = \)\(\dfrac{1}{2}\) ( sđ\(\overparen{AnD} + \) sđ\(\overparen{CpB}\))
Câu 3 :
Cho bốn điểm A, B, C, D thuộc đường tròn \(\left( O \right).\) Biết \(\widehat {BOD} = {130^0}\) thì số đo \(\widehat {BAD}\) là:
Đáp án : D Phương pháp giải :
Sử dụng góc nội tiếp bằng một nửa số đo của cung bị chắn, số đo góc ở tâm bằng số đo cung bị chắn. Lời giải chi tiết :
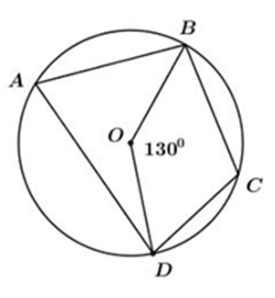 Ta có: \(\widehat {BOD} = {130^0} \) nên \(sđ\,\overparen{BD} = {130^0}\). Do đó \(\widehat {BAD} = \dfrac{1}{2}sđ\overparen{BD} = {65^0}\) (góc nội tiếp bằng một nửa số đo của cung bị chắn)
Câu 4 :
Cho hình vẽ bên. Mệnh đề nào sau đây là sai. 
Đáp án : D Phương pháp giải :
Sử dụng mối liên hệ giữa góc nội tiếp và góc ở tâm cùng chắn một cung: Số đo góc nội tiếp bằng nửa số đo góc ở tâm chắn cung đó. Lời giải chi tiết :
Ta có \(\widehat {AMB} = \widehat {ANB}\) vì hai góc nội tiếp cùng chắn cung \(AB.\) Ta lại có $\widehat {AMB} = \dfrac{1}{2}\widehat {AOB},\widehat {\,\,ANB} = \dfrac{1}{2}\widehat {AOB}$ ( mối liên hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung \(AB)\)
Câu 5 :
Cho hình vẽ (hai đường tròn có tâm là \(B,C \) và điểm \(B\) nằm trên đường tròn tâm \(C\)). Biết $\widehat {MAN} = {20^0}.$  Khi đó \(\widehat {PCQ} = ?\)
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc nội tiếp và góc ở tâm Số đo của góc nội tiếp bằng nửa số đo cung bị chắn Số đo góc ở tâm bằng số đo cung bị chắn Lời giải chi tiết :
Ta nhận thấy \(\widehat {MAN}\) nội tiếp đường tròn tâm \(B\), chắn cung nhỏ \(MN\) của đường tròn \(\left( B \right)\) nên \(\widehat {MAN} = \dfrac{1}{2}\widehat {MBN} = {20^0} \) suy ra \(\widehat {MBN} = {40^0} \) hay \(\widehat {PBQ} = {40^0}.\) Ta lại có \(\widehat {PBQ}\) là góc nội tiếp đường tròn tâm \(C\) và \(\widehat {PCQ}\) là góc ở tâm của \(\left( C \right)\) nên $\widehat {PBQ} = \dfrac{1}{2}\widehat {PCQ}$ suy ra $\widehat {PCQ} = 2\widehat {PBQ} = {80^0}.$ Vậy \(\widehat {PCQ} = {80^0}.\)
Câu 6 :
Cho đường tròn \(\left( O \right)\) Trên \(\left( O \right)\) lấy ba điểm \(A,B,D\) sao cho \(\widehat {AOB} = {120^0},\,\,AD = BD.\)  Khi đó \(\Delta ABD\) là:
Đáp án : A Phương pháp giải :
Sử dụng mối liên hệ về số đo góc ở tâm và số đo góc nội tiếp để tính góc $\widehat {ADB}$ của tam giác $ABD$ Từ đó dựa vào điều kiện đề bài để suy ra tính chất tam giác $ABD$ Lời giải chi tiết :
Từ mối liên hệ về số đo góc ở tâm và số đo góc nội tiếp ta có $\widehat {ADB} = \dfrac{1}{2}\widehat {AOB} = \dfrac{1}{2}{.120^0} = {60^0}.$ \(\Delta ABD\) có \(AD = BD\) nên cân tại \(D,\) có một góc $\widehat {ADB}=60^0$ nên \(\Delta ABD\) là tam giác đều.
Câu 7 :
Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) cắt nhau tại \(A\) và \(B.\) Vẽ cát tuyến \(CAD\) vuông góc với \(AB\left( {C \in \left( O \right),D \in \left( {O'} \right)} \right)\) . Tia \(CB\) cắt \(\left( {O'} \right)\) tại \(E,\) tia \(DB\) cắt \(\left( O \right)\) tại \(F.\) Khi đó
Đáp án : C Phương pháp giải :
Sử dụng tính chất các góc nội tiếp cùng chắn một cung thì bằng nhau Lời giải chi tiết :
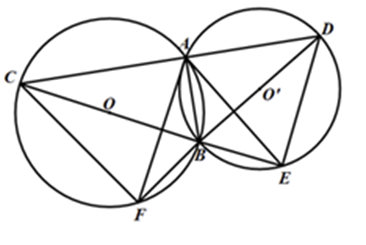 Theo giả thiết ta có \(CD \bot AB\) nên \(\widehat {CAB} = {90^0}.\) Mà \(\widehat {CAB} = \dfrac{1}{2}sđ\overparen{BC} \Rightarrow sđ \overparen{BC} = {180^0}.\) Vậy ba điểm \(B,\,O,\,C\) thẳng hàng. Chứng minh tương tự ta nhận được \(B,\,\,O',\,D\) thẳng hàng. Trong \(\left( O \right)\) các góc \(\widehat {CAF},\,\widehat {CBF}\) là các góc nội tiếp cùng chắn chung \(CF\) nên $\widehat {CAF} = \,\widehat {CBF}.\,\left( 1 \right)$ Trong \(\left( {O'} \right)\) các góc \(\widehat {DAE},\,\widehat {DBE}\) là các góc nội tiếp cùng chắn chung \(DE\) nên \(\widehat {DAE} = \widehat {DBE}\,\left( 2 \right).\) Mặt khác \(\widehat {CBF},{\kern 1pt} \widehat {DBE}\) là các góc đối đỉnh, do đó \(\widehat {CBF} = \widehat {DBE}\,\,\left( 3 \right).\) Từ \(\left( 1 \right),\,\left( 2 \right),\,\left( 3 \right)\) ta suy ra \(\widehat {CAF} = \widehat {DAE}.\)
Câu 8 :
Cho đường tròn \(\left( {O;R} \right)\) và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Khi đó tứ giác \(ABEC\) là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc nội tiếp chắn nửa đường tròn Sử dụng dấu hiệu nhận biết các hình đặc biệt Lời giải chi tiết :
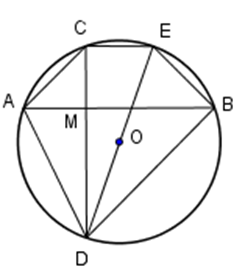 Do \(DE\) là đường kính của \(\left( {O;R} \right)\) nên \(\widehat {DCE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn). Do đó \(CD \bot CE.\) Mặt khác theo giả thiết ta có \(CD \bot AB.\) Do đó \(AB//CE.\) Vậy tứ giác \(ABEC\) là hình thang \(\left( 1 \right).\) Mặt khác các dây \(CE,AB\) là hai dây song song của \(\left( O \right)\) chắn hai cung \(AC\) và \(BE\) nên Cung \(AC = \) cung \(BE \) \( \Rightarrow AC=BE\,\,\,\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra tứ giác \(ABEC\) là hình thang cân.
Câu 9 :
Cho hình vẽ dưới đây.  Khi đó mệnh đề đúng là:
Đáp án : B Phương pháp giải :
- Tính chất góc có đỉnh nằm trong đường tròn: Số đo góc có đỉnh nằm trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn. - Tính chất góc có đỉnh nằm ngoài đường tròn: Số đo góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn. Lời giải chi tiết :
Ta áp dụng công thức về góc có đỉnh ở trong và ở ngoài đường tròn bị chắn bởi cung ta nhận được \(\left\{ \begin{array}{l}\widehat {AQB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} + sđ\overparen{CdM}} \right)\,\,\\\widehat {ANB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} - sđ\overparen{CdM}} \right)\,\,\end{array} \right. \)\(\Rightarrow \widehat {AQB} = \dfrac{1}{2}\left( {sđ\overparen{AeB} + sđ\overparen{CdM}} \right) > \dfrac{1}{2}\left( {sđ\overparen{AeB} - sđ\overparen{CdM}} \right) = \widehat {ANB}.\)
Câu 10 :
Cho tam giác \(ABC\) cân tại \(A\) nội tiếp đường tròn tâm \(O.\) Trên \(\left( O \right)\) lấy điểm \(D\) thuộc cung \(AC\). Gọi \(E = AC \cap BD,\,\,F = AD \cap BC.\) Khi đó mệnh đề đúng là:
Đáp án : D Phương pháp giải :
Áp dụng tính chất góc nội tiếp, góc có đỉnh nằm ngoài đường tròn, các cung chắn hai dây bằng nhau để chứng minh \(\widehat {AFB} = \widehat {ABD}.\) Lời giải chi tiết :
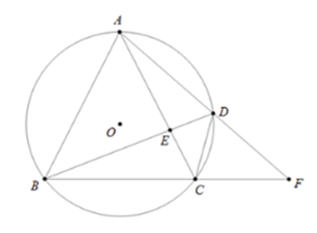 \(\Delta ABC\) cân tại \(A\) nên \(AB = AC\) suy ra \(sđ\,\overparen{AB} = sđ\,\overparen{AC}.\) Áp dụng kết quả trên và theo tính chất của góc ngoài đường tròn ta có: $\widehat {AFB} = \dfrac{1}{2}\left( {sđ\,\overparen{AB} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}\left( {sđ\,\overparen{AC} - sđ\,\overparen{CD}} \right) = \dfrac{1}{2}sđ\,\overparen{AD}.$ Mặt khác theo tính chất góc nội tiếp ta có \(\widehat {ABD} = \dfrac{1}{2}sđ\,\overparen{AD}.\) Do đó \(\widehat {AFB} = \widehat {ABD}.\)
Câu 11 :
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng AP cắt RQ tại S. Khi đó:
Đáp án : D Phương pháp giải :
- Sử dụng tính chất tia phân giác của một góc nội tiếp chia cung bị chắn thành hai cung bằng nhau. - Tính chất góc có đỉnh nằm bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn. Lời giải chi tiết :
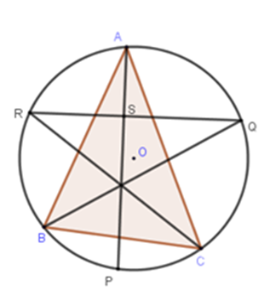 Ta có tia phân giác \(AP\) chia đôi cung \(BC\) thành hai cung bằng nhau, hay\(sđ\overparen{BP} = sđ\overparen{CP}=\dfrac{1}{2}sđ\,\overparen{BC}.\) Tương tự ta có $sđ\overparen{AQ} = sđ\overparen{CQ}=\dfrac{1}{2}sđ\,\overparen{AC} $$sđ\overparen{AR} = sđ\overparen{BR}=\dfrac{1}{2}sđ\,\overparen{AB} .$ Khi đó theo tính chất của góc có đỉnh bên trong đường tròn ta có \(\begin{array}{l}\widehat {ASQ} = \dfrac{1}{2}\left( {sđ\,\overparen{AQ} + sđ\,\overparen{PR}} \right)\\ = \dfrac{1}{2}\left( {\dfrac{1}{2}sđ\,\overparen{AC} + \dfrac{1}{2}sđ\,\overparen{AB} + \dfrac{1}{2}sđ\,\overparen{BC}} \right) \\= \dfrac{1}{2}\left( {\dfrac{1}{2}{{.360}^0}} \right) = {90^0}.\end{array}\)
Câu 12 :
Cho tam giác nhọn \(ABC\,\,\left( {AB > BC} \right)\) nội tiếp đường tròn \(\left( O \right).\) \(D\) là điểm chính giữa cung \(AC.\) Giả sử \(\{E\} = AB \cap CD,\,\,\{F\} = AD \cap BC.\) Khi đó :
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc có đỉnh nằm ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn. Lời giải chi tiết :
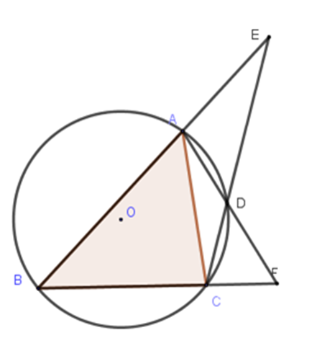 Theo tính chất của góc ngoài đường tròn ta có \(\left\{ \begin{array}{l}\widehat {AED} = \dfrac{1}{2}\left( {sđ\,\overparen{BC} - sđ\,\overparen{AD}} \right)\\\widehat {CFD} = \dfrac{1}{2}\left( {sđ\,\overparen{AB} - sđ\,\overparen{CD}} \right)\end{array} \right.\,\,\left( 1 \right).\) Theo đề bài ta có \(AB > BC \Rightarrow sđ\,\overparen{BC} < sđ\,\overparen{AB}\,\,\left( 2 \right).\) Mặt khác ta có \(D\) là điểm chính giữa cung \(AC\) nên \(sđ\,\overparen{AD} = sđ\,\overparen{CD}\,\left( 3 \right).\) Từ \(\left( 1 \right),\,\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\widehat {AED} < \widehat {CFD}.\)
Câu 13 :
Cho hình vẽ, biết số đo cung \(BmD\) là \({120^0}.\) Khi đó 
Đáp án : D Phương pháp giải :
Tính góc $BOD$ rồi suy ra góc $BOA$ Từ đó ta tính được góc $OAB$ Lời giải chi tiết :
Xét $(O)$ có $\widehat {BOD} = sđ \overparen{BmD}=120^0$ mà góc $BOD$ và $AOB$ là hai góc kề bù nên \(\widehat {AOB} = 180^\circ - \widehat {BOD} = 60^\circ \) Xét tam giác $AOB$ vuông tại $B$ (do $AB$ là tiếp tuyến) nên \( \widehat {AOB} + \widehat {OAB} = 90^\circ \Rightarrow \widehat {OAB} = 90^\circ - 60^\circ = 30^\circ \) Chú ý
Các em có thể sử dụng tính chất góc có đỉnh nằm ngoài đường tròn để tính \(\widehat {OAB}\).
Câu 14 :
Cho đường tròn tâm \(O,\) đường kính \(AB.\) Lấy điểm \(P\) khác \(A\) và \(B\) trên đường tròn sao cho \(\widehat {BAP} = {30^0}.\) Gọi \(T\) là giao điểm của \(AP\) với tiếp tuyến tại \(B\) của đường tròn. Khi đó ta có \(\widehat {PBT} = ?\)
Đáp án : A Phương pháp giải :
Sử dụng tính chất góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau. Lời giải chi tiết :
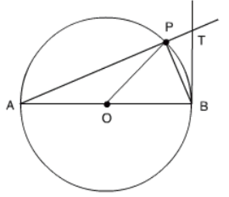 Xét $(O)$ có góc $PAB$ là góc nội tiếp chắn cung $BP$, góc $PBT$ là góc tạo bởi tia tiếp tuyến và dây cung $BP$ nên \(\widehat {PBT} = \widehat {PAB} = 30^\circ \)
Câu 15 :
Cho hình vẽ ở bên. Biết \( \widehat {BAx}=20^0\).  Hãy tính số đo của cung bị chắn \(AB.\)
Đáp án : D Phương pháp giải :
Sử dụng góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn Lời giải chi tiết :
Do \(Ax\) là tiếp tuyến với \(\left( O \right)\) tại \(A\) nên \(\widehat {BAx} = \dfrac{1}{2}\) sđ\(\overparen{AB}\) hay sđ \(\overparen{AB}= 2\widehat {BAx} = {2.20^0} = {40^0}\) Vì vậy sđ\(\overparen{AB} = {40^0}.\)
Câu 16 :
Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) kẻ hai cát tuyến \(ABC\) và \(ADE\) với đường tròn đó (\(B\) nằm giữa \(A\) và \(C,\)\(D\) nằm giữa \(A\) và \(E\)). Kẻ dây \(BF//DE.\) Khi đó kết luận đúng là:
Đáp án : B Phương pháp giải :
Sử dụng các tính chất góc nội tiếp chắn một cung, góc đỉnh nằm ngoài đường tròn, cung bị chắn giữa hai dây song song, tam giác đồng dạng để chứng minh \(\Delta ACE \backsim \Delta DCF \Rightarrow AC.DF = AE.DC\). Lời giải chi tiết :
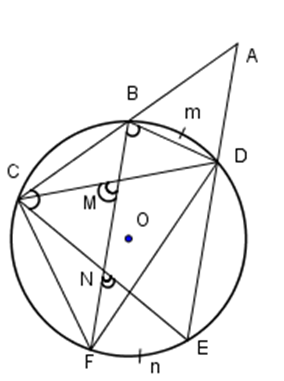 Ta có \(\widehat {BCD}\) là góc nội tiếp chắn cung \(BmD\,\,\left( 1 \right).\) Ta có \(\widehat {FCE}\) là góc nội tiếp chắn cung \(FnE\,\,\left( 2 \right).\) Mặt khác ta có \(sđ\overparen{BmD}\, = sđ\overparen{FnE}\,\,\left( 3 \right).\) (hai cung bị chắn bởi hai dây song song) Từ \(\left( 1 \right),\,\left( 2 \right),\,\left( 3 \right)\) suy ra \(\widehat {FCE} = \widehat {BCD} \Rightarrow \widehat {FCE} + \widehat {ECD} = \widehat {BCD} + \widehat {ECD}.\) Do đó \(\widehat {FCD} = \widehat {ECB}\,\left( 4 \right).\) Theo tính chất về góc có đỉnh bên ngoài đường tròn ta có \(\widehat {CAE} = \dfrac{1}{2}\left( {sđ\overparen{CFE} - sđ\overparen{BmD}} \right) = \dfrac{1}{2}\left( {sđ\,\overparen{CFE} - sđ\overparen{FnE}} \right) = \dfrac{1}{2}sđ\,\overparen{CF}\,\,\left( 5 \right).\) Theo tính chất của góc nội tiếp bị chắn bởi cung ta có $\widehat {CDF} = \dfrac{1}{2}sđ\overparen{CF}\,\,\left( 6 \right).$ Từ \(\left( 5 \right)\) và \(\left( 6 \right)\) ta nhận được \(\widehat {CAE} = \widehat {CDF}\,\,\left( 7 \right).\) Từ \(\left( 4 \right)\) và \(\left( 7 \right)\) ta nhận được \(\Delta ACE \backsim \Delta DCF\) (g-g) Do đó \(\dfrac{{AC}}{{DC}} = \dfrac{{AE}}{{DF}} = \dfrac{{CE}}{{CF}} \Rightarrow AC.DF = AE.DC.\)
Câu 17 :
Từ điểm \(M\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(MA, MB\) với \(\left( O \right)\) tại \(A\) và \(B.\) Qua \(A\) vẽ đường thẳng song song với \(MB\) cắt đường tròn tại \(C.\) .PNG) Nối \(C\) với \(M\) cắt đường tròn \(\left( O \right)\) tại \(D.\) Nối \(A\) với \(D\) cắt \(MB\) tại \(E.\) Chọn câu đúng
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn 1 cung. Sử dụng tính chất tam giác đồng dạng. Lời giải chi tiết :
Xét \(\Delta ABE\) và \(\Delta BDE\) có: + \(\widehat E\) chung. + \(\widehat {BAE} = \widehat {DBE}\) (góc nội tiếp và góc giữa tia tiếp tuyến và dây cung cùng chắn cung $BD$ ) Do đó ta có \(\Delta ABE \backsim \Delta BDE\,\left( {g.g} \right)\). \( \Rightarrow \dfrac{{AE}}{{BE}} = \dfrac{{BE}}{{DE}} \Rightarrow E{B^2} = AE.DE\,\,\left( 1 \right).\) Ta có: \(MB//AC \Rightarrow \widehat {EMD} = \widehat {DCA}\) (hai góc so le trong) Mà \(\widehat {DCA} = \widehat {MAD}\) (góc nội tiếp và góc giữa tiếp tuyến và dây cung cùng chắn cung \(AD\)) Do đó \(\widehat {EMD} = \widehat {MAD}\). Xét \(\Delta MEA\) và \(\Delta DEM\) có: \(\widehat E\) chung. \(\widehat {EMD} = \widehat {MAD}\) (cmt) Suy ra \(\Delta MEA \backsim \Delta DEM\,.\) Do đó \(\dfrac{{ME}}{{DE}} = \dfrac{{EA}}{{EM}} \Rightarrow M{E^2} = DE.EA\,\,\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(2\) ta nhận được \(E{B^2} = E{M^2} \Rightarrow EB = EM.\)
Câu 18 :
Cho điểm \(C\) thuộc nửa đường tròn \(\left( O \right)\) đường kính \(AB.\) Từ điểm \(D\) thuộc đọan \(AO\) kẻ đường thẳng vuông góc với \(AO\) cắt \(AC\) và \(BC\) lần lượt lại \(E\) và \(F.\) Tiếp tuyến tại \(C\) với nửa đường tròn cắt $EF$ tại \(M\) và cắt \(AB\) tại \(N.\) Khi đó 
Đáp án : A Lời giải chi tiết :
Ta có \(\widehat {MCA} = \dfrac{1}{2}\) sđ \(\overparen{AC}\) (góc giữa tiếp tuyến và dây cung chắn cung \(AC\)) \(\left( 1 \right).\) Lại có \(\widehat {MEC} = \widehat {AED} = {90^0} - \widehat {EAD} = {90^0} - \dfrac{1}{2}\) sđ \(\overparen{BC} = \dfrac{1}{2}\) sđ \(\overparen{AC}\,\,\,\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {MCE} = \widehat {MEC}.\) Vậy \(\Delta MEC\) cân tại \(M,\) suy ra \(MC = ME.\) Chứng minh tương tự ta có \(MC = MF.\) Suy ra \(ME = MF.\)
Câu 19 :
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(BC = R.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(B,C\) cắt nhau tại \(A.\) Gọi \(M\) là giao điểm của \(AO\) và \(BC.\) Khi đó tam giác \(AMB\) là:
Đáp án : D Phương pháp giải :
+ Sử dụng góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn + Tổng ba góc trong tam giác bằng $180^0$ Lời giải chi tiết :
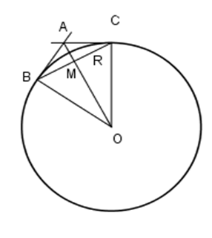 Xét đường tròn $(O)$ có dây \(BC = R = OC = OB\) nên \(\Delta BOC\) là tam giác đều. Do đó \(\widehat {BOC} = {60^0} \Rightarrow \) sđ \(\overparen{BC} = {60^0}\) Lại có \(\widehat {ABC}\) là góc tạo bởi hai tiếp tuyến \(BA\) và dây cung \(BC\) của \(\left( O \right).\) Do góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo cung bị chắn nên \(\widehat {ABC} = \dfrac{1}{2}\) sđ \(\overparen{BC} = {30^0}\). Lại có $AB=AC$ (tính chất hai tiếp tuyến cắt nhau) và $OB=OC=R$ nên $AO$ là đường trung trực của $BC$ Hay $AO \bot BC$ tại $M$, suy ra \(\widehat {AMB} = {90^0} \Rightarrow \widehat {BAM} = {60^0}.\) Như vậy tam giác $AMB$ vuông tại $M$ và có \(\widehat {ABM} = {30^0};\, \widehat {BAM} = {60^0}\) Nên đáp án A, B đều đúng. Ta lại có \(\sin \widehat {ABM} = \dfrac{{AM}}{{AB}} \Rightarrow \dfrac{{AM}}{{AB}} = \sin \,{30^0} = \dfrac{1}{2}.\) Hay cạnh góc vuông \(AM\) bằng nửa cạnh huyền \(AB.\) Vì vậy đáp án C cũng đúng.
Câu 20 :
Cho hình vẽ. Khi đó đáp án đúng là 
Đáp án : B Phương pháp giải :
Sử dụng các tính chất: - Góc nội tiếp cùng chắn một cung trong một đường tròn thì bằng nhau. - Tổng ba góc trong một tam giác bằng \({180^0}\). Lời giải chi tiết :
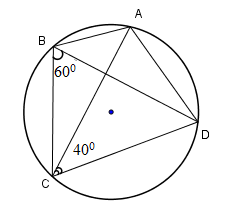 Xét $(O)$ có $\widehat {CAD} = \widehat {CBD}$ (cùng chắn cung \(CD\) ). Do đó ta có \(\widehat {CAD} = {60^0}.\) Tổng ba góc trong một tam giác bằng \({180^0}\) Nên: $\begin{array}{l}\,\,\,\,\,\,\widehat {CAD} + \widehat {ACD} + \widehat {ADC} = {180^0}\\ \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat {CAD} + \widehat {ACD}} \right) \\= {180^0} - \left( {{{60}^0} + {{40}^0}} \right) = {80^0}.\end{array}$
Câu 21 :
Tia phân giác góc \(\widehat {BAD}\) của hình bình hành \(ABCD\) cắt các đường thẳng \(BC\) và \(DC\) lần lượt tại hai điểm \(M\) và \(N.\) Dựng ra phía ngoài hình bình hành \(ABCD\) tam giác \(MCO\) cân tại $O$ với \(\widehat {MOC} = \widehat {BAD}\). Khi đó:
Đáp án : A Phương pháp giải :
Sử dụng dấu hiệu hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau thì tứ giác đó là tứ giác nội tiếp. Lời giải chi tiết :
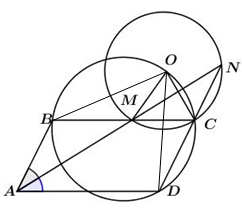 Ta có \(BM//AD\) nên \(\widehat {BMA} = \widehat {MAD}.\) Mặt khác \(AM\) là phân giác của \(\widehat {BAD}\) nên \(\widehat {BAM} = \widehat {MAD}.\) Từ đó \(\widehat {BAM} = \widehat {AMB.}\) Vậy \(\Delta ABM\) cân tại \(B.\) Suy ra \(BM = BA = DC.\) Tam giác \(OMC\) cân tại \(O\) nên \(OM = OC\) và \(\widehat {OMC} = \widehat {OCM} \)\(= \dfrac{{180^\circ - \widehat {MOC}}}{2} \)\(= \dfrac{1}{2}\left( {180^\circ - \alpha } \right)\) Đặt \(\alpha = \widehat {BAD},\) ta có \(\widehat {OCD} \)\(= \widehat {BCD} + \widehat {OCM} \)\(= \alpha + \dfrac{1}{2}\left( {{{180}^0} - \alpha } \right) \)\(= {90^0} + \dfrac{\alpha }{2}\,\,\left( 1 \right).\) Các góc \(\widehat {BMO},\,\widehat {OMC}\) kề bù nên \(\widehat {BMO} = {180^0} - \,\widehat {OMC} = {180^0} - \,\widehat {OCM} = {90^0} + \dfrac{\alpha }{2}\,\,\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\widehat {OCD} = \widehat {BMO}.\) Xét hai tam giác \(\Delta OBM,\,\Delta ODC\) có \(\left\{ \begin{array}{l}\widehat {OCD} = \widehat {BMO}\\OM = OC \, (cmt)\\BM = CD \, (cmt)\end{array} \right.\) nên \(\Delta OBM = \Delta ODC\,\,\left( {c.g.c} \right).\) Do đó \(\widehat {OBM} = \widehat {ODC}.\) Điều này chứng tỏ \(BOCD\) là tứ giác nội tiếp. Do đó bốn điểm \(B,\,O,\,C,\,D\) thuộc cùng một đường tròn.
Câu 22 :
Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O \right),\) các đường cao\(AD,\,BE,\,CF\,\left( {D \in BC,\,E \in AC,\,F \in AB} \right)\) cắt nhau tại \(H\). Khi đó ta có
Đáp án : C Phương pháp giải :
Sử dụng các tính chất: - Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau. - Tính chất tam giác đồng dạng thì các cạnh tương ứng tỉ lệ. Lời giải chi tiết :
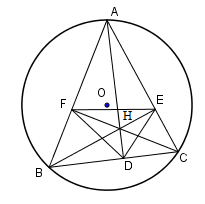 Do \(AD,\,BE\) là các đường cao nên \(\widehat {HDC} = \widehat {HEC} = {90^0}.\) Do đó $\widehat {HDC} + \widehat {HEC} = {90^0} + {90^0} = {180^0}.$ Vậy tứ giác \(DCEH\) là tứ giác nội tiếp. Các góc \(\widehat {HED},\,\widehat {HCD}\) cùng chắn cung \(HD\) nên \(\widehat {HED} = \,\widehat {HCD}\,\,\left( 1 \right).\) Xét hai tam giác \(\Delta BDE,\,\,\Delta BHC\) có \(\widehat {HED} = \,\widehat {HCD}\,\) (theo \(\left( 1 \right)\) ) và góc \(\widehat {EBC}\) chung. Do đó \(\Delta BDE \backsim \,\Delta BHC.\) Từ đó ta nhận được \(\dfrac{{BD}}{{BH}} = \dfrac{{BE}}{{BC}} \Rightarrow BH.BE = BC.BD.\) Đáp án A đúng. Chứng minh tương tự ta có \(\Delta CHB \backsim \Delta CDF\,\left( {g - g} \right) \Leftrightarrow \dfrac{{CH}}{{CD}} = \dfrac{{CB}}{{CF}}\) hay \(CH.CF = CD.CB.\) Đáp án B đúng. Vậy cả A, B đều đúng.
Câu 23 :
Cho nửa đường tròn tâm \(O,\) đường kính \(AB = 2R.\) Đường thẳng qua \(O\) và vuông góc \(AB\) cắt cung \(AB\) tại \(C.\) Gọi \(E\) là trung điểm \(BC.\,AE\) cắt nửa đường tròn \(O\) tại \(F.\) Đường thẳng qua \(C\) và vuông góc $AF$ tại \(G\) cắt \(AB\) tại $H.$ Khi đó góc \(\widehat {OGH}\) có số đo là:
Đáp án : A Phương pháp giải :
+ Sử dụng tính chất tứ giác nội tiếp $ACGO$ và tính chất hai góc phụ nhau + Dấu hiệu nhận biết tứ giác nội tiếp: tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau thì tứ giác đó nội tiếp. Lời giải chi tiết :
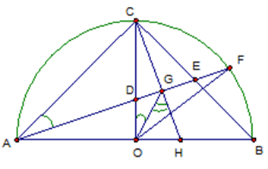 Theo giả thiết ta có \(OC \bot AB,\,CG \bot AG\) nên ta suy ra \(\widehat {AOC} = \widehat {AGC} = {90^0}.\) Nói cách khác \(O,\,G\) cùng nhìn \(AC\) dưới một góc vuông. Kéo theo \(\widehat {OGA} = \widehat {OCA}.\) Mà \(\Delta OAC\) vuông cân tại O nên \(\widehat {OCA} = {45^0}.\) Suy ra \(\widehat {OGA} = {45^0}.\) Ta lại có \(\widehat {OGH} + \widehat {OGA} = \widehat {HGA} = \widehat {AGC} = {90^0} \)\(\Rightarrow \widehat {OGH} = {90^0} - \widehat {OGA} = {90^0} - {45^0} = {45^0}.\) Do đó \(\widehat {OGH} = {45^0}\)
Câu 24 :
Cho hình vuông \(ABCD\) có cạnh \(2R.\)  Diện tích \(S\) phần màu xanh trong hình vuông \(ABCD\) là
Đáp án : A Phương pháp giải :
Tính các diện tích hình vuông \(ABCD\), các hình quạt \(AEH,BHG,CGF,DFE\). Diện tích phần màu xanh là hiệu giữa diện tích hình vuông và các hình quạt. Lời giải chi tiết :
Gọi \(S,\,{S_1},\,{S_2}\) lần lượt là diện tích phần màu xanh, diện tích hình vuông và diện tích phần còn lại. Khi đó ta có \({S_1} = {\left( {2R} \right)^2}=4R^2\,\,\left( 1 \right).\) Nhận thấy mỗi hình quạt \(AEH,BHG,CGF,DFE\) là \(\dfrac{1}{4}\) hình tròn bán kính \(R= \dfrac{{AB}}{2}\) Nên tổng diện tích \(4\) hình quạt \(AEH,BHG,CGF,DFE\) chính bằng diện tích của hình tròn bán kính $R$ . Hay \({S_2} = \pi {R^2}\,\,\left( 2 \right).\) Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(S = 4{R^2} - \pi {R^2}.\) Cho đường tròn \(\left( {O;R} \right),\) đường kính \(AB\) cố định, đường kính \(CD\) thay đổi \(\left( {CD \ne AB} \right).\) Các tia \(BC,\,BD\) cắt tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) lần lượt tại \(E,\,F.\) Câu 25
Tứ giác \(DCEF\) là
Đáp án : C Phương pháp giải :
Sử dụng dấu hiệu nhận biết tứ giác nội tiếp: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó là tứ giác nội tiếp. Lời giải chi tiết :
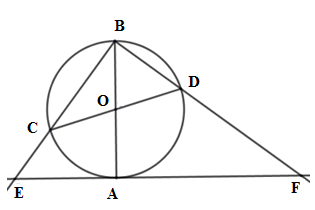 Xét \(\left( O \right)\) có \(AB;CD\) là các đường kính nên \(\widehat {CBD} = 90^\circ \) Xét tam giác \(BCD\) vuông tại \(B\) có \(\widehat {BCD} + \widehat {BDC} = 90^\circ \) mà \(\widehat {OBD} = \widehat {ODB}\) (do \(\Delta OBD\) cân tại \(O\) ) Nên \(\widehat {BCD} + \widehat {OBD} = 90^\circ \Rightarrow \widehat {BCD} = 90^\circ - \widehat {OBD}\) (1) Xét tam giác \(ABF\) vuông tại \(A\) (vì $EF$ là tiếp tuyến của $(O)$) có \(\widehat {BFA} = 90^\circ - \widehat {ABF}\) (2) Từ (1) và (2) suy ra \(\widehat {BCD} = \widehat {DFA}\) Do đó tứ giác \(DCEF\) là tứ giác nội tiếp (dấu hiệu góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó) Câu 26
Khi \(CD\) thay đổi. Giá trị nhỏ nhất của \(EF\) theo \(R\) là:
Đáp án : A Phương pháp giải :
Sử dụng hệ thức giữa đường cao và cạnh trong tam giác vuông để tính \(AE.AF = A{B^2}\). Sử dụng bất đẳng thức Cô-si để tìm GTNN của $EF$. Lời giải chi tiết :
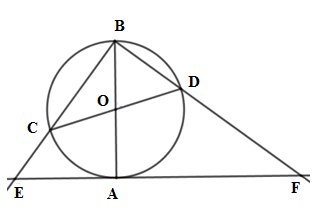 \(B\) thuộc đường tròn $(O)$ đường kính \(CD.\) Suy ra \(\widehat {DBC} = {90^0}.\) Xét \(\Delta EBF\) có \(\widehat {EBF} = {90^0},\,BA \bot EF \Rightarrow AE.AF = A{B^2}\). Theo bất đẳng thức Cô-si cho \(\left( {AE,AF} \right)\) ta có \(EF = AE + AF \ge 2\sqrt {AE.AF} = 2\sqrt {A{B^2}} = 2AB = 4R.\) Vậy giá trị nhỏ nhất của \(EF\) là \(4R.\) đạt được khi \(CD \bot AB.\) Cho \(BC\) là một dây cung của đường tròn \(\left( {O;R} \right),\,\,\left( {BC \ne 2R} \right).\) Điểm \(A\) di động trên cung lớn \(BC\) sao cho \(O\) luôn nằm trong tam giác \(ABC.\) Các đường cao \(AD,\,BE,\,CF\) của tam giác \(ABC\) đồng quy tại \(H.\) Câu 27
Chọn kết luận sai:
Đáp án : A Phương pháp giải :
Sử dụng các dấu hiệu nhận biết tứ giác nội tiếp: - Tổng hai góc đối bằng \({180^0}\). - Hai đỉnh kề nhau cùng nhìn về cạnh đối diện các góc bằng nhau. - Sử dụng trường hợp đồng dạng góc – góc để chứng minh các tam giác đồng dạng. Lời giải chi tiết :
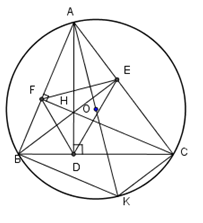 Theo giả thiết ta có \(CF,\,BE\) là các đường cao của tam giác \(ABC\) nên \(CF \bot AB,\,BE \bot AC.\) Do đó \(\widehat {BFC} = {90^0},\,\widehat {BEC} = {90^0}.\) Theo dấu hiệu nhận biết tứ giác nội tiếp ta suy ra \(BFEC\) là tứ giác nội tiếp nên C đúng. \( \Rightarrow \widehat {AFE} = \widehat {ACB}\) (cùng bù với \(\widehat {BFE}\)) Xét hai tam giác $AEF$ và \(ABC\) có \(\widehat A\) chung; \(\widehat {AFE} = \widehat {ACB}\left( {cmt} \right) \Rightarrow \Delta AEF \backsim \Delta ABC\left( {g.g} \right)\) nên B đúng. Lại có \(\widehat {HEC} + \widehat {HDC} = {90^0} + {90^0} = {180^0}\) nên tứ giác \(CDHE\) là tứ giác nội tiếp nên D đúng. Câu 28
Kẻ đường kính \(AK\) của đường tròn \(\left( {O;R} \right).\) Khi đó \(BHCK\) là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất góc nội tiếp chắn nửa tròn để chứng minh \(\widehat {ABK} = \widehat {ACK} = {90^0}\). Sử dụng định lý từ vuông góc đến song song để chứng minh \(BK//CF;CK//BE\). Sử dụng dấu hiệu nhận biết các hình đặc biệt. Lời giải chi tiết :
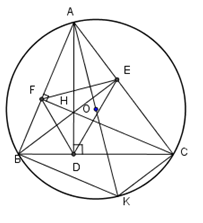 Theo giả thiết ta có \(CF\) là đường cao của \(\Delta ABC\) nên $AF \bot CF\,\left( 1 \right).$ Mặt khác \(AK\) là đường kính của \(\left( O \right)\) nên theo tính chất của góc nội tiếp chắn nửa đường tròn ta suy ra $\widehat {ABK} = {90^0} \Rightarrow BK \bot AB\,\,\left( 2 \right).$ Từ \(\left( 1 \right),\,\left( 2 \right)\) suy ra \(HC//BK\,\,\left( 3 \right).\) Chứng minh tương tự ta có \(BH//CK\,\,\left( 4 \right).\) Từ \(\left( 3 \right),\,\left( 4 \right)\) ta nhận được \(BHCK\) là hình bình hành.
Câu 29 :
Cho \(A\) là điểm cố định trên đường tròn \(\left( {O;R} \right).\) Gọi \(AB\) và \(AC\) là hai dây cung thay đổi trên đường tròn \(\left( O \right)\) thỏa mãn \(\sqrt {AB.AC} = R\sqrt 3 .\) Khi đó vị trí của \(B,\,C\) trên \(\left( O \right)\) để diện tích \(\Delta ABC\) lớn nhất là:
Đáp án : B Phương pháp giải :
Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$ Sử dụng tính chất góc nội tiếp chắn nửa đường tròn để chứng minh \(\widehat {ABD} = {90^0} \Rightarrow \Delta ABD \backsim \Delta AHC\). Tính độ dài \(AH\) từ tính chất hai tam giác đồng dạng, từ đó suy ra điều kiện để diện tích tam giác \(ABC\) lớn nhất. Lời giải chi tiết :
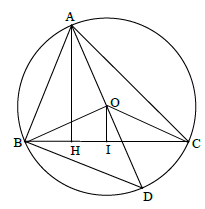 Kẻ \(AH \bot BC,\,OI \bot BC\), đường kính $AD.$ Ta chứng minh được \(\Delta AHC \backsim \Delta ABD\,\left( {g - g} \right).\) Do đó \(\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC \)\(\Rightarrow AB.AC = 2R.AH\,\,\left( 1 \right).\) Theo giả thiết \(\sqrt {AB.AC} = R\sqrt 3 ,\) nên \(AB.AC = 3{R^2}\,\,\left( 2 \right).\) Thay \(\left( 2 \right)\) và \(\left( 1 \right)\) ta có \(AH = \dfrac{{3R}}{2}.\) Lại có \(OI + OA \ge AI \ge AH\) nên \(OI \ge AH - OA = \dfrac{{3R}}{2} - R = \dfrac{R}{2}.\) Do \(AH = \dfrac{{3R}}{2}\) là giá trị không đổi nên \({S_{ABC}}\) lớn nhất khi \(BC\) lớn nhất \( \Leftrightarrow OI\) nhỏ nhất \( \Leftrightarrow OI = \dfrac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow \Delta ABC\) cân tại \(A\). Mà \(OI = \dfrac{R}{2} \Rightarrow \sin \widehat {OBI} \)\(= \dfrac{{OI}}{{OB}} = \dfrac{1}{2}\)\( \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} \)\(\Rightarrow \widehat {BOC} \)\(= {120^0}\)$ \Rightarrow \widehat {BAC} = {60^0}$ Vậy \(\Delta ABC\) đều. Chú ý
HS thường làm sai như sau: Diện tích tam giác \(ABC\) lớn nhất khi \(BC = 2R,AH = R\) mà không để ý đến điều kiện \(\sqrt {AB.AC} = R\sqrt 3 \).
|



















Danh sách bình luận