Trắc nghiệm Bài 2: Liên hệ giữa cung và dây Toán 9Đề bài
Câu 1 :
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Câu 2 :
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
Câu 3 :
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Câu 4 :
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
Câu 5 :
Chọn khẳng định đúng.
Câu 6 :
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
Câu 7 :
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
Câu 8 :
Cho tam giác $ABC$ có $\widehat B = 60^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào đúng khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
Câu 9 :
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 3 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Câu 10 :
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là đúng?
Cho đường tròn $(O)$ đường kính $AB$ và đường tròn $(O')$ đường kính $AO$. Các điểm $C,D$ thuộc đường tròn $(O)$ sao cho $B \in $ cung $CD$ và cung $BC$ nhỏ hơn cung $BD$. Các dây cung $AC$ và $AD$ cắt đường tròn $(O')$ theo thứ tự $E$ và $F$. Câu 11
So sánh dây $OE$ và $OF$ của đường tròn $(O')$.
Câu 12
So sánh dây $AE$ và $AF$ của đường tròn $(O')$.
Lời giải và đáp án
Câu 1 :
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung. Lời giải chi tiết :
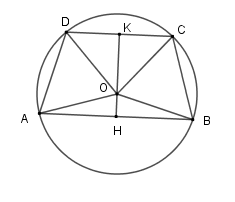 Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$. Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$ $ \Rightarrow \widehat {DOK} = \widehat {COK}$ Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$ $ \Rightarrow \widehat {AOH} = \widehat {BOH}$ Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$ Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$. Phương án A, C, D sai, B đúng. Chú ý
Lời giải trên chính là một cách chứng minh cho tính chất “Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.”
Câu 2 :
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
Đáp án : A Lời giải chi tiết :
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau: +) Cung lớn hơn căng dây lớn hơn. +) Dây lớn hơn căng cung lớn hơn. Nên dây $AB > CD$ thì cung $AB$ lớn hơn cung $CD$
Câu 3 :
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung. Lời giải chi tiết :
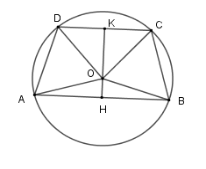 Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$. Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$$ \Rightarrow \widehat {DOK} = \widehat {COK}$ Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$$ \Rightarrow \widehat {AOH} = \widehat {BOH}$ Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$ Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$. Phương án A, C, D sai và B đúng. Chú ý
Lời giải trên chính là một cách chứng minh cho tính chất “Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.”
Câu 4 :
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
Đáp án : D Phương pháp giải :
Sử dụng liên hệ giữa dây và đường kính để so sánh các góc ở tâm từ đó so sánh các cung và dây cung Lời giải chi tiết :
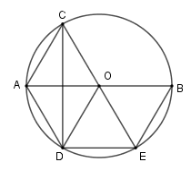 Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD}$ Suy ra cung $AD$ bằng cung $AC$ nên dây $AD = AC$ Lại thấy $\widehat {AOC} = \widehat {BOE}$ (đối đỉnh) nên cung $AC$ bằng cung $BE$ suy ra dây $AC = BE$. Phương án A, B, C đúng.
Câu 5 :
Chọn khẳng định đúng.
Đáp án : A Lời giải chi tiết :
+) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy. +) Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy. +) Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
Câu 6 :
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 66^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung lớn nhất?
Đáp án : C Phương pháp giải :
Sử dụng mối liên hệ giữa cung và dây Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau: +) Cung lớn hơn căng dây lớn hơn. +) Dây lớn hơn căng cung lớn hơn. +) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại Lời giải chi tiết :
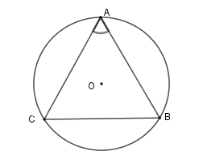 Vì tam giác $ABC$ cân tại $A$ có $\widehat A = 66^\circ \Rightarrow \widehat B = \widehat C = \dfrac{{180^\circ - \widehat A}}{2} = \dfrac{{180^\circ - 66^\circ }}{2} = 57^\circ $ Vì $\widehat A > \widehat B = \widehat C$ nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có $BC > AB = AC$ Theo mối liên hệ giữa cung và dây ta có $\overparen{BC}$ $ > $ $\overparen{AB}$ $ = $ $\overparen{AC}$.
Câu 7 :
Cho đường tròn $\left( {O;R} \right)$ và hai dây $AB;CD$ sao cho $\widehat {AOB} = 120^\circ ;\widehat {COD} = 60^\circ $. So sánh các dây $CD;AB$.
Đáp án : D Phương pháp giải :
Sử dụng mối liên hệ giữa cung và dây Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau: +) Cung lớn hơn căng dây lớn hơn. +) Dây lớn hơn căng cung lớn hơn. +) Hai cung bằng nhau căng hai dây bằng nhau và ngược lại Sử dụng định lý: Trong một đường tròn, đường kính là dây có độ dài lớn nhất Lời giải chi tiết :
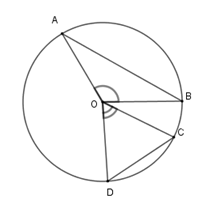 Vì $\widehat {COD} < \widehat {AOB}$ nên cung $CD$ nhỏ hơn cung $AB$, từ đó dây $CD < AB$ (*) Xét tam giác $OCD$ cân tại $O$ có $\widehat {COD} = 60^\circ $ nên $\Delta COD$ là tam giác đều $ \Rightarrow CD = R$ $AB$ là dây không đi qua tâm nên $AB < 2R \Rightarrow AB < 2CD$ (**) Từ (*) và (**) ta có $CD < AB < 2CD$
Câu 8 :
Cho tam giác $ABC$ có $\widehat B = 60^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào đúng khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
Đáp án : D Phương pháp giải :
Sử dụng mối liên hệ giữa cung và dây Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau: Hai cung bằng nhau căng hai dây bằng nhau và ngược lại Lời giải chi tiết :
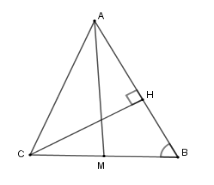 Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng $HB;MB;MH$. Xét tam giác $BCH$ vuông tại $H$ có $\cos B = \dfrac{{HB}}{{BC}} \Leftrightarrow \dfrac{{HB}}{{BC}} = \cos 60^\circ = \dfrac{1}{2} \Rightarrow HB = \dfrac{{BC}}{2} = BM = CM$ Xét tam giác $HBM$ có $BM = BH$ (cmt) và $\widehat {ABC} = 60^\circ $ nên $\Delta HBM$ là tam giác đều $ \Rightarrow BM = BH = HM$ Suy ra ba cung $HB;MB;MH$ bằng nhau.
Câu 9 :
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 3 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Đáp án : A Phương pháp giải :
Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau Sử dụng mối liên hệ giữa dây và đường kính Sử dụng định lý Pytago Lời giải chi tiết :
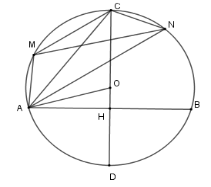 Vì hai dây $MC{\rm{//}}AN$ nên hai cung $AM$ và cung $CN$ bằng nhau, hay $AM = CN$ Suy ra $MCNA$ là hình thang cân $ \Rightarrow MN = AC$. Gọi $H$ là giao của $CD$ và $AB$. Khi đó vì $AB \bot CD$ tại $H$ nên $H$ là trung điểm của $AB \Rightarrow AH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 3 }}{2}$ Xét tam giác vuông $AHO$, theo định lý Pytago ta có $OH = \sqrt {A{O^2} - A{H^2}} = \dfrac{R}{2}$$ \Rightarrow CH = \dfrac{{3R}}{2}$ Theo định lý Pytago cho tam giác $ACH$ vuông ta có $AC = \sqrt {C{H^2} + A{H^2}} = R\sqrt 3 $ Vậy $MN = R\sqrt 3 $.
Câu 10 :
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là đúng?
Đáp án : C Phương pháp giải :
Bước 1: Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau để chứng minh $AC = ED$ Bước 2: Sử dụng định lý Pytago để chứng minh hệ thức. Lời giải chi tiết :
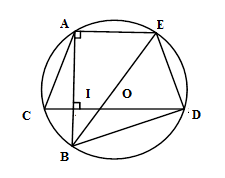 Xét $\left( O \right)$ có $BE$ là đường kính và $A \in \left( O \right)$$ \Rightarrow AE \bot AB$ mà $CD \bot AB$$ \Rightarrow AE{\rm{//}}CD$ Nên cung $AC$ bằng cung $ED$ hay $AC = ED.$ Xét các tam giác vuông $\Delta IAC$ và $\Delta IBD$ ta có $I{A^2} + I{C^2} = A{C^2};$ $I{B^2} + I{D^2} = B{D^2} $ $\Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} $ $= A{C^2} + B{D^2} $ $= E{D^2} + B{D^2}$ Mà $\Delta BED$ vuông tại $D$ nên $E{D^2} + B{D^2} = E{B^2} = {\left( {2R} \right)^2} = 4{R^2}$ Vậy $I{A^2} + I{C^2} + I{B^2} + I{D^2} = 4{R^2}$. Cho đường tròn $(O)$ đường kính $AB$ và đường tròn $(O')$ đường kính $AO$. Các điểm $C,D$ thuộc đường tròn $(O)$ sao cho $B \in $ cung $CD$ và cung $BC$ nhỏ hơn cung $BD$. Các dây cung $AC$ và $AD$ cắt đường tròn $(O')$ theo thứ tự $E$ và $F$. Câu 11
So sánh dây $OE$ và $OF$ của đường tròn $(O')$.
Đáp án : B Lời giải chi tiết :
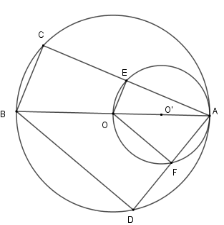 Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$ Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$ $ \Rightarrow $ $E$ là trung điểm của $AC$ $ \Rightarrow $ $OE = \dfrac{1}{2}BC.$ Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ nhỏ hơn cung $BD$ nên $BC < BD \Rightarrow OE < OF$ . Câu 12
So sánh dây $AE$ và $AF$ của đường tròn $(O')$.
Đáp án : A Phương pháp giải :
Sử dụng định lý Pytago Lời giải chi tiết :
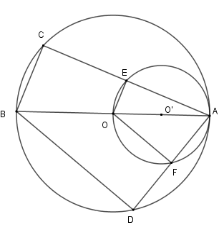 Theo định lý Pytago ta có : $A{E^2} = A{O^2} - O{E^2}$ và $A{F^2} = A{O^2} - A{E^2}$ mà $OE < OF$ $ \Rightarrow A{E^2} > A{F^2} \Rightarrow AE > AF$.
|



















Danh sách bình luận