Trắc nghiệm Bài 1: Hình trụ. Diện tích xung quanh và thể tích hình trụ Toán 9Đề bài
Câu 1 :
Cho hình trụ có chu vi đáy là $8\pi $ và chiều cao \(h = 10\) . Tính thể tích hình trụ.
Câu 2 :
Cho hình trụ có bán kính đáy \(R = 4\,\left( {cm} \right)\) và chiều cao \(h = 5\,\left( {cm} \right)\) . Diện tích xung quanh của hình trụ là
Câu 3 :
Cho hình trụ có bán kính đáy \(R = 8\,cm\) và diện tích toàn phần \(564\pi \)\(c{m^2}\) . Tính chiều cao của hình trụ.
Câu 4 :
Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\) . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
Câu 5 :
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
Câu 6 :
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 25\pi \,c{m^2}\) và chiều cao \(h = 10\,cm\) . Nếu trục lăn đủ \(12\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu? 
Câu 7 :
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là \(3\,cm\) .
Câu 8 :
Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
Câu 9 :
Cho hình trụ bị cắt bỏ một phần \(OABB'A'O'\) như hình vẽ. Thể tích phần còn lại là: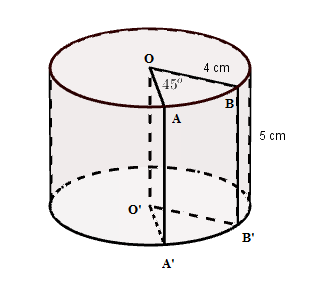 
Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$ Câu 10
Chọn khẳng định sai.
Câu 11
Biết $BC = 25cm$ và $AH = 12cm.$ Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác $ADHE$ quay quanh $AD.$
Lời giải và đáp án
Câu 1 :
Cho hình trụ có chu vi đáy là $8\pi $ và chiều cao \(h = 10\) . Tính thể tích hình trụ.
Đáp án : C Phương pháp giải :
Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\) để tính bán kính đáy Sử dụng công thức tính thể tích hình trụ bán kính \(R\) và chiều cao \(h\): \(V = \pi {R^2}h\) Lời giải chi tiết :
Ta có chu vi đáy \(C = 2\pi R = 8\pi\) suy ra \(R = 4\) Thể tích hình trụ là \(V = \pi {R^2}h = \pi {.4^2}.10 = 160\pi \) (đvtt).
Câu 2 :
Cho hình trụ có bán kính đáy \(R = 4\,\left( {cm} \right)\) và chiều cao \(h = 5\,\left( {cm} \right)\) . Diện tích xung quanh của hình trụ là
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình trụ bán kính \(R\) và chiều cao \(h\) \({S_{xq}} = 2\pi Rh\) Lời giải chi tiết :
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh = 2\pi .4.5 = 40\pi \,\,\left( {c{m^2}} \right)\)
Câu 3 :
Cho hình trụ có bán kính đáy \(R = 8\,cm\) và diện tích toàn phần \(564\pi \)\(c{m^2}\) . Tính chiều cao của hình trụ.
Đáp án : B Phương pháp giải :
Sử dụng công thức tính diện tích toàn phần của hình trụ ${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2}$ để tính bán kính đáy Lời giải chi tiết :
Diện tích toàn phần của hình trụ là: ${S_{tp}} = {S_{xq}} + {S_{2d}} = 2\pi Rh + 2\pi {R^2} = 564\pi $ Suy ra \(16\pi h + 2\pi {.8^2} = 564\pi\) Do đó \(h = 27,25\,(cm)\)
Câu 4 :
Cho hình trụ có bán kính đáy \(R\) và chiều cao \(h\) . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
Đáp án : C Phương pháp giải :
Sử dụng các công thức tính chu vi đáy, diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ. Lời giải chi tiết :
Chiều cao mới của hình trụ là \(h' = 2h\); bán kính đáy mới là \(R' = \dfrac{R}{2}\) Hình trụ mới có: Chu vi đáy: \(2\pi R' = 2\pi \dfrac{R}{2} = \pi R < 2\pi R = C\) nên phương án D sai. Diện tích toàn phần: \(2\pi R'h + 2\pi {R'^2} = 2\pi Rh + \dfrac{{\pi {R^2}}}{2} \ne 2\pi Rh + 2\pi {R^2}\) nên phương án B sai. Thể tích: \(\pi {R'^2}h = \dfrac{{\pi {R^2}h}}{4} \ne \pi {R^2}h\) nên phương án A sai. Diện tích xung quanh: \(2\pi R'h = 2\pi .\dfrac{R}{2}.2h = 2\pi Rh\) nên phương án C đúng.
Câu 5 :
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 12cm\) và đường kính đáy là \(d= 8\,cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
Đáp án : D Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và diện tích một đáy ${S_d} = \pi {R^2}.$ Lời giải chi tiết :
Bán kính đường tròn đáy \(R = \dfrac{8}{2} = 4\,cm\) nên diện tích một đáy ${S_d} = \pi {R^2} = 16\pi \,(c{m^2})$ Ta có diện tích xung quanh của hình trụ: ${S_{xq}} = 2\pi Rh = 2\pi .4.12 = 96\pi \,(c{m^2})$ Vì hộp sữa đã mất nắp nên diện tích các mặt của hộp sữa là: \(96\pi + 16\pi = 112\pi \,\left( {c{m^2}} \right).\)
Câu 6 :
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy \(S = 25\pi \,c{m^2}\) và chiều cao \(h = 10\,cm\) . Nếu trục lăn đủ \(12\) vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
Đáp án : A Phương pháp giải :
Sử dụng diện tích đáy ${S_{_d}} = \pi {R^2}$ để tính bán kính \(R\) . Sử dụng công thức tính diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ Lời giải chi tiết :
Bán kính \(R\) của đường tròn đáy là \(\pi {R^2} = 25\pi \) suy ra \( R = 5\,cm\) Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .5.10 = 100\pi \left( {c{m^2}} \right)\) Vì trục lăn \(12\) vòng nên diện tích tạo trên sân phẳng là \(12.100\pi = 1200\pi \,\left( {c{m^2}} \right)\)
Câu 7 :
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là \(3\,cm\) .
Đáp án : C Phương pháp giải :
Sử dụng công thức diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ và công thức diện tích toàn phần \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\) Lời giải chi tiết :
Từ giả thiết ta cóL \(2\pi Rh + 2\pi {R^2} = 2.2.\pi Rh\) \(Rh = {R^2}\) \(R = h\) . Vậy chiều cao của hình trụ là $3\,cm$ .
Câu 8 :
Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
Đáp án : A Phương pháp giải :
Sử dụng công thức diện thể tích của hình trụ $V = \pi {R^2}h$ và công thức diện tích toàn phần \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\) Sử dụng bất đẳng thức Cô-si cho ba số dương \(a,b,\,c\) là \(a + b + c \ge 3\sqrt[3]{{abc}}\) Dấu “=” xảy ra khi \(a = b = c\) Lời giải chi tiết :
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(R,\,\,h\,\,\left( {R > 0;\,h > 0} \right)\) Ta có \(V = \pi {R^2}h\) suy ra \(h = \dfrac{V}{{\pi {R^2}}}\) Diện tích toàn phần của hình trụ là: \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi R.\dfrac{V}{{\pi {R^2}}} + 2\pi {R^2} = \dfrac{{2V}}{R} + 2\pi {R^2}\) \( = \dfrac{V}{R} + \dfrac{V}{R} + 2\pi {R^2} \ge 3\sqrt[3]{{\dfrac{V}{R}.\dfrac{V}{R}.2\pi {R^2}}} = 3\sqrt[3]{{2\pi {V^2}}}\) (theo bất đẳng thức Cosi) Dấu “=” xảy ra khi \(\dfrac{V}{R} = 2\pi {R^2}\) suy ra \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\) Vậy với \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\) thì \({S_{tp}}\) đạt giá trị nhỏ nhất là \(3\sqrt[3]{{2\pi {V^2}}}\).
Câu 9 :
Cho hình trụ bị cắt bỏ một phần \(OABB'A'O'\) như hình vẽ. Thể tích phần còn lại là:
Đáp án : A Phương pháp giải :
Dựa vào hình vẽ tính xem phần cắt đi chiếm bao nhiêu phần thể tích hình trụ. Sử dụng công thức tính thể tích hình trụ $V = \pi R^2h$. Từ đó suy ra thể tích phần còn lại sau khi cắt. Lời giải chi tiết :
Phần hình trụ bị cắt đi chiếm \(\dfrac{{45^\circ }}{{360^\circ }} = \dfrac{1}{8}\) (hình trụ) Thể tích phần còn lại là \(V = \dfrac{7}{8}\pi {R^2}h = \dfrac{7}{8}\pi {.4^2}.5 = 70\pi \,\,\left( {c{m^3}} \right)\) Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$ Câu 10
Chọn khẳng định sai.
Đáp án : D Phương pháp giải :
Sử dụng dấu hiệu nhận biết hình chữ nhật và hệ thức lượng trong tam giác vuông Lời giải chi tiết :
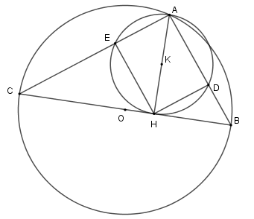 Xét \(\left( O \right)\) có $\widehat {CAD} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn) Xét \(\left( K \right)\) có \(\widehat {AEH} = \widehat {ADH} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) Nên tứ giác $ADHE$ là hình chữ nhật ( vì có ba góc vuông)\( \Rightarrow \) phương án A đúng. Xét tam giác vuông \(AHB\) có \(A{H^2} = AD.AB \Rightarrow \) phương án C đúng Xét tam giác vuông \(A{H^2} = AC.AE\) nên \(AD.AB = AC.AE \Rightarrow \) phương án B đúng Câu 11
Biết $BC = 25cm$ và $AH = 12cm.$ Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác $ADHE$ quay quanh $AD.$
Đáp án : B Phương pháp giải :
Sử dụng hệ thức lượng để tính cạnh \(AD,\,HD\) Sử dụng công thức diện tích xung quanh của hình trụ ${S_{xq}} = 2\pi Rh$ Lời giải chi tiết :
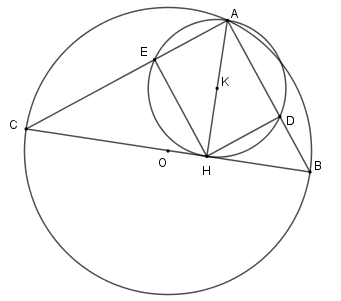 Xét tam giác vuông \(ABC\) có \(HB.HC = A{H^2} \Leftrightarrow HB.HC = 144\) và \(HB + HC = BC \Leftrightarrow HB + HC = 25\) Suy ra \(HB = 9\,cm;\,HC = 16\,cm\) (Chú ý: $AB < AC$ nên $HB < HC$). Xét tam giác vuông \(AHB\) có \(\dfrac{1}{{H{D^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{B^2}}} \Rightarrow HD = \dfrac{{36}}{5}\,cm\) Tương tự ta có $HE = \dfrac{{48}}{5}cm \Rightarrow AD = \dfrac{{48}}{5}\,cm$. Khi quay hình chữ nhật \(ADHE\) quanh \(AD\) ta được hình trụ có chiều cao \(AD\) và bán kính đáy \(HD\). Nên ${S_{xq}} = 2.\pi HD.AD = \dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)$
|
