Trắc nghiệm Bài tập ôn tập chương 8 Toán 9Đề bài
Câu 1 :
Chọn câu sai. Cho hình trụ có bán kính đáy là \(R\) và chiều cao \(h\) . Khi đó
Câu 2 :
Chọn câu sai.
Câu 3 :
Tính diện tích xung quanh của một hình trụ có bán kính đáy là $4\,cm$ và chiều cao là \(6\,cm\) .
Câu 4 :
Diện tích toàn phần của một hình trụ có chu vi đường tròn đáy là $12\,cm$ và chiều cao là \(4\,cm\) là
Câu 5 :
Một hình trụ có bán kính đáy bằng \(5\,cm\) và diện tích xung quanh bằng \(300\pi \,\left( {c{m^2}} \right)\) . Chiều cao của hình trụ là
Câu 6 :
Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh. Tính chiều cao hình trụ biết bán kính hình trụ là $1cm.$
Câu 7 :
Một hình trụ có chiều cao bằng đường kính đáy. Biết thể tích của nó là \(54\pi \,\left( {c{m^3}} \right).\) Tính diện tích toàn phần của hình trụ.
Câu 8 :
Một hình nón có bán kính đáy bằng \(5cm\) , chiều cao bằng \(12\,cm.\)Tính diện tích xung quanh của hình nón.
Câu 9 :
Tính thể tích của một hình nón cụt có các bán kính đáy bằng \(4 cm\) và \(7cm\), chiều cao bằng \(11 cm.\)
Câu 10 :
Cho hai hình trụ. Hình trụ thứ nhất có bán kính đáy bằng nửa bán kính đáy của hình trụ thứ hai và có chiều cao gấp bốn lần chiều cao của hình trụ thứ hai. Tỉ số các thể tích của hình trụ thứ nhất và hình trụ thứ hai bằng:
Câu 11 :
Một hình nón có diện tích xung quanh bằng $960\;c{m^2}$ , chu vi đáy bằng $48\,\left( {cm} \right).$ Đường sinh của hình nón đó bằng
Câu 12 :
Một hình nón có bán kính đáy bằng \(r\) và diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của hình nón theo \(r.\)
Câu 13 :
Một hình nón và một hình trụ có bán kính đáy bằng nhau và chiều cao bằng nhau. Tỉ số các thể tích của hình trụ và hình nón bằng
Câu 14 :
Tính bán kính của một hình cầu biết thể tích của hình cầu bằng $123\,\left( {c{m^3}} \right)$ (làm tròn đến số thập phân thứ nhất). Lấy \(\pi = 3,14.\)
Câu 15 :
Chiều cao của một hình trụ gấp rưỡi bán kính đáy của nó. Tỉ số thể tích của hình trụ này và thể tích hình cầu có bán kính bằng bán kính đáy của hình trụ là:
Câu 16 :
Một hình cầu được đặt khít bên trong một hình trụ, biết đường kính hình cầu là \(20\,cm.\) Tính thể tích hình trụ. 
Câu 17 :
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)
Câu 18 :
Một hình nón có bán kính đáy bằng $2\,cm,$ chiều cao bằng đường kính một hình cầu. Diện tích toàn phần hình nón bằng diện tích mặt cầu. Tính chiều cao hình nón.
Lời giải và đáp án
Câu 1 :
Chọn câu sai. Cho hình trụ có bán kính đáy là \(R\) và chiều cao \(h\) . Khi đó
Đáp án : D Lời giải chi tiết :
Ta có hình trụ có bán kính đáy là \(R\) và chiều cao \(h\) . Khi đó + Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh\) nên A đúng + Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\) nên B đúng + Thể tích khối trụ là \(V = \pi {R^2}h\) nên C đúng, D sai.
Câu 2 :
Chọn câu sai.
Đáp án : B Phương pháp giải :
Áp dụng các công thức liên quan đến hình nón và hình cầu Lời giải chi tiết :
Ta có + Thể tích hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(V = \dfrac{1}{3}\pi {R^2}h\) nên A đúng + Diện tích hình cầu có bán kính \(R\) là \(S = 4\pi {R^2}\) nên C đúng + Đường sinh của hình nón có chiều cao \(h\) và bán kính đáy \(R\) là \(l = \sqrt {{R^2} + {h^2}} \) nên D đúng + Thể tích khối cầu có bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\) nên B sai.
Câu 3 :
Tính diện tích xung quanh của một hình trụ có bán kính đáy là $4\,cm$ và chiều cao là \(6\,cm\) .
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\) Lời giải chi tiết :
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi {.4}.6 = 48\pi \,\left( {c{m^2}} \right).\)
Câu 4 :
Diện tích toàn phần của một hình trụ có chu vi đường tròn đáy là $12\,cm$ và chiều cao là \(4\,cm\) là
Đáp án : C Phương pháp giải :
Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\) để tính bán kính đáy Sử công thức tính diện tích toàn phần hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{tp}} = 2\pi {R}h + 2\pi {R^2}\) Lời giải chi tiết :
Gọi \(R\) là bán kính đường tròn đáy ta có \(12 = 2\pi R \Rightarrow R = \dfrac{6}{\pi }\,\left( {cm} \right)\) Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi .\dfrac{6}{\pi }.4 + 2\pi .{\left( {\dfrac{6}{\pi }} \right)^2} \) \( = 48+ \dfrac{{72}}{\pi }\,\left( {c{m^2}} \right)\)
Câu 5 :
Một hình trụ có bán kính đáy bằng \(5\,cm\) và diện tích xung quanh bằng \(300\pi \,\left( {c{m^2}} \right)\) . Chiều cao của hình trụ là
Đáp án : A Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\) Lời giải chi tiết :
Gọi chiều cao của hình trụ là \(h.\) Ta có \({S_{xq}} = 2\pi R.h \Leftrightarrow 2\pi {.5}.h = 300\pi \Leftrightarrow h = 30\,cm.\)
Câu 6 :
Một hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh. Tính chiều cao hình trụ biết bán kính hình trụ là $1cm.$
Đáp án : B Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh, diện tích toàn phần của hình trụ có bán kính đáy $R$ và chiều cao \(h\) là \({S_{xq}} = 2\pi {R}h\) ; \({S_{tp}} = 2\pi {R}h + 2\pi {R^2}\) Lời giải chi tiết :
Gọi chiều cao của hình trụ là \(h.\) Ta có \({S_{xq}} = 2\pi {R}h\) ; \({S_{tp}} = 2\pi {R}h + 2\pi {R^2}\) mà theo giả thiết thì \({S_{tp}} = 2{S_{xq}}\) nên ta có \(2\pi {R}h + 2\pi {R^2} = 2.2\pi {R}h \Leftrightarrow 2\pi {R^2} = 2\pi {R}h \)\(\Rightarrow h = R=1cm.\)
Câu 7 :
Một hình trụ có chiều cao bằng đường kính đáy. Biết thể tích của nó là \(54\pi \,\left( {c{m^3}} \right).\) Tính diện tích toàn phần của hình trụ.
Đáp án : D Phương pháp giải :
Hình trụ có bán kính đáy $R$ và chiều cao \(h\) có diện tích toàn phần là \({S_{tp}} = 2\pi {R^2}h + 2\pi {R^2}\), thể tích là \(V = \pi {R^2}h.\) Lời giải chi tiết :
Gọi hình trụ có bán kính đáy $R$ và chiều cao \(h\) , từ đề bài suy ra \(h = 2R\) . Khi đó \(V = \pi {R^2}h \Leftrightarrow \pi .{R^2}.2R = 54\pi \Rightarrow {R^3} = 27 \Rightarrow R = 3\,cm\) nên \(h = 2R = 6\,cm.\) Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi .Rh + 2\pi {R^2} = 2\pi .3.6 + 2\pi {.3^2} = 54\pi \,\left( {c{m^2}} \right)\)
Câu 8 :
Một hình nón có bán kính đáy bằng \(5cm\) , chiều cao bằng \(12\,cm.\)Tính diện tích xung quanh của hình nón.
Đáp án : A Phương pháp giải :
Công thức tính diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\) với \(R\) là bán kính đáy, \(l\) là đường sinh của hình nón và \(l = \sqrt {{R^2} + {h^2}} \) , \(h\) là chiều cao hình nón. Lời giải chi tiết :
Đường sinh của hình nón là \(l = \sqrt {{R^2} + {h^2}} = \sqrt {{5^2} + {{12}^2}} = 13.\) Diện tích xung quanh hình nón là \({S_{xq}} = \pi Rl = \pi .5.13 = 65\pi \,\,\left( {c{m^2}} \right)\)
Câu 9 :
Tính thể tích của một hình nón cụt có các bán kính đáy bằng \(4 cm\) và \(7cm\), chiều cao bằng \(11 cm.\)
Đáp án : B Phương pháp giải :
Sử dụng công thức tính thể tích hình nón cụt $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})$ với các bán kính đáy là $R$ và $r,$chiều cao $h.$ Lời giải chi tiết :
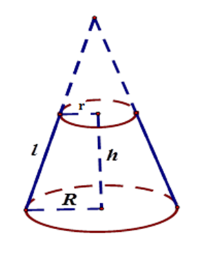 Thể tích nón cụt là $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}) = \dfrac{1}{3}.\pi .11\left( {{4^2} + 4.7 + {7^2}} \right) = 341\pi \,\,\left( {c{m^3}} \right)$
Câu 10 :
Cho hai hình trụ. Hình trụ thứ nhất có bán kính đáy bằng nửa bán kính đáy của hình trụ thứ hai và có chiều cao gấp bốn lần chiều cao của hình trụ thứ hai. Tỉ số các thể tích của hình trụ thứ nhất và hình trụ thứ hai bằng:
Đáp án : A Phương pháp giải :
Hình trụ có bán kính đáy $R$ và chiều cao \(h\) có thể tích là \(V = \pi {R^2}h.\) Lời giải chi tiết :
Giả sử hình trụ thứ nhất có bán kính đáy là \(R\) và chiều cao là \(h.\) Thể tích hình trụ thứ nhất là: ${V_1} = \pi {R^2}h$ (1) Từ (1) và (2) suy ra \({V_1} = {V_2} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = 1\)
Câu 11 :
Một hình nón có diện tích xung quanh bằng $960\;c{m^2}$ , chu vi đáy bằng $48\,\left( {cm} \right).$ Đường sinh của hình nón đó bằng
Đáp án : D Phương pháp giải :
Sử dụng công thức tính chu vi đường tròn đáy \(C = 2\pi R\) và công thức tính diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\) với \(R\) là bán kính đáy, \(l\) là đường sinh của hình nón. Lời giải chi tiết :
Gọi \(R\) là bán kính đáy và \(l\) là đường sinh của hình nón. Vì chu vi đáy là $48\left( {cm} \right) \Rightarrow 2\pi R = 48\, \Rightarrow R = \dfrac{{24}}{\pi }\,cm.$ Diện tích xung quanh \({S_{xq}} = \pi Rl \Leftrightarrow \pi .\dfrac{{24}}{\pi }.l = 960 \Rightarrow l = 40\,cm\)
Câu 12 :
Một hình nón có bán kính đáy bằng \(r\) và diện tích xung quanh gấp đôi diện tích đáy. Tính thể tích của hình nón theo \(r.\)
Đáp án : C Phương pháp giải :
Sử dụng công thức tính diện tích xung quanh hình nón \({S_{xq}} = \pi Rl\) và công thức thể tích $V = \dfrac{1}{3}\pi {R^2}h$ với \(R\) là bán kính đáy, \(l\) là đường sinh của hình nón, \(h\) là chiều cao của hình nón. Sử dụng mối quan hệ ${R^2} + {h^2} = {l^2}$ Lời giải chi tiết :
Gọi \(l\) là đường sinh của hình nón, \(h\) là chiều cao của hình nón. Ta có diện tích xung quanh hình nón là \({S_{xq}} = \pi Rl\), diện tích đáy là \(S = \pi {r^2}\) Vì diện tích xung quanh gấp đôi diện tích đáy nên \(\pi rl = 2\pi {r^2} \Rightarrow l = 2r\) Vì ${r^2} + {h^2} = {l^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} = \sqrt {{{\left( {2r} \right)}^2} - {r^2}} = r\sqrt 3 $ Khi đó thể tích khối nón là \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {r^2}.\sqrt 3 r = \dfrac{{\sqrt 3 }}{3}\pi {r^3}\)
Câu 13 :
Một hình nón và một hình trụ có bán kính đáy bằng nhau và chiều cao bằng nhau. Tỉ số các thể tích của hình trụ và hình nón bằng
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích hình nón ${V_n} = \dfrac{1}{3}\pi {R^2}h$ và công thức tính thể tích hình trụ ${V_t} = \pi {R^2}h$ Lời giải chi tiết :
Vì hình nón và một hình trụ có bán kính đáy bằng nhau và chiều cao bằng nhau nên gọi \(h\) là chiều cao và \(R\) là bán kính đáy khi đó thể tích hình nón ${V_n} = \dfrac{1}{3}\pi {R^2}h$ và thể tích hình trụ ${V_t} = \pi {R^2}h$ Tỉ số thể tích của hình trụ và hình nón là \(\dfrac{{{V_t}}}{{{V_n}}} = \dfrac{{\pi {R^2}h}}{{\dfrac{1}{3}\pi {R^2}h}} = 3.\)
Câu 14 :
Tính bán kính của một hình cầu biết thể tích của hình cầu bằng $123\,\left( {c{m^3}} \right)$ (làm tròn đến số thập phân thứ nhất). Lấy \(\pi = 3,14.\)
Đáp án : C Phương pháp giải :
Sử dụng công thức tính thể tích khối cầu có bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\) Lời giải chi tiết :
Gọi bán kính mặt cầu là \(R\) thì thể tích khối cầu là \(V = \dfrac{4}{3}\pi {R^3}\)\( \Leftrightarrow \dfrac{4}{3}.3,14.{R^3} = 123 \Leftrightarrow R \approx 3,1\,cm\)
Câu 15 :
Chiều cao của một hình trụ gấp rưỡi bán kính đáy của nó. Tỉ số thể tích của hình trụ này và thể tích hình cầu có bán kính bằng bán kính đáy của hình trụ là:
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích hình trụ: $V = \pi {R^2}h$ và thể tích hình cầu \(V = \dfrac{4}{3}\pi {R^3}.\) Lời giải chi tiết :
Giả sử hình trụ có bán kính đáy \(R.\) Suy ra chiều cao của nó là \(1,5R.\) Thể tích hình trụ là \({V_1} = \pi {R^2}h = \pi {R^2}.1,5R = 1,5\pi {R^3}\) Thể tích hình cầu có bán kính \(R\) là \({V_2} = \dfrac{4}{3}\pi {R^3}\) \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{1,5\pi {R^3}}}{{\dfrac{4}{3}\pi {R^3}}} = \dfrac{9}{8}.\)
Câu 16 :
Một hình cầu được đặt khít bên trong một hình trụ, biết đường kính hình cầu là \(20\,cm.\) Tính thể tích hình trụ.
Đáp án : D Phương pháp giải :
Sử dụng công thức tính thể tích hình trụ: $V = \pi {r^2}h$ Lời giải chi tiết :
Bán kính hình cầu là \(r = 20:2 = 10\,cm\) Vì hình cầu nội tiếp hình trụ nên bán kính hình cầu bằng bán kính đáy hình trụ và đường kính hình cầu bằng chiều cao hình trụ. Do đó hình trụ có bán kính đáy là \(r = 10\,cm\) và chiều cao là \(h = 2r = 20\,cm\) Thể tích hình trụ là \(V = \pi {r^2}h = \pi {.10^2}.20 = 2000\pi \,\left( {c{m^3}} \right)\)
Câu 17 :
Cho một hình trụ, một hình nón và một hình cầu có thể tích bằng nhau. Bán kính đáy của hình trụ, bán kính đáy của hình nón và bán kính của hình cầu đều bằng $R.$ Tính các chiều cao \({h_1}\) của hình trụ và \({h_2}\) của hình nón theo \(R.\)
Đáp án : B Phương pháp giải :
Sử dụng công thức + Thể tích hình trụ : $V = \pi {R^2}{h_1}$. + Thể tích hình nón : $V = \dfrac{1}{3}\pi {R^2}{h_2}.$ + Thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}\) Cho ba thể tích trên bằng nhau rồi giải hệ để tìm ${h_1};{h_2}$ Lời giải chi tiết :
+ Thể tích hình trụ : ${V_1} = \pi {R^2}{h_1}$. + Thể tích hình nón : ${V_2} = \dfrac{1}{3}\pi {R^2}{h_2}.$ + Thể tích hình cầu : \({V_3} = \dfrac{4}{3}\pi {R^3}\) Ta có ${V_1} = {V_2} = {V_3}$ Nên \(\left\{ \begin{array}{l}\pi {R^2}{h_1} = \dfrac{4}{3}\pi {R^3}\\\dfrac{1}{3}\pi {R^2}{h_2} = \dfrac{4}{3}\pi {R^3}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{h_1} = \dfrac{4}{3}R\\{h_2} = 4R\end{array} \right.\)
Câu 18 :
Một hình nón có bán kính đáy bằng $2\,cm,$ chiều cao bằng đường kính một hình cầu. Diện tích toàn phần hình nón bằng diện tích mặt cầu. Tính chiều cao hình nón.
Đáp án : C Phương pháp giải :
+ Tính đường sinh của hình nón \(l = \sqrt {{R^2} + {h^2}} \) + Tính diện tích toàn phần hình nón: ${S_{tp}} = {S_{xq}} + {S_d} = \pi Rl + \pi {R^2}.$ + Sử dụng công thức tính diện tích mặt cầu: $S = 4\pi {R^2}$ Dựa vào đề bài để có phương trình từ đó tìm được \(h.\) Lời giải chi tiết :
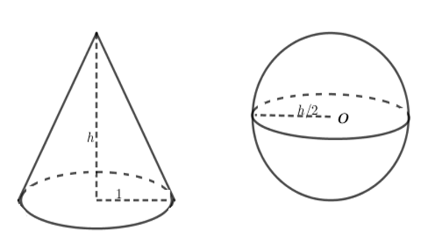 Gọi \(h\) là chiều cao hình nón \(\left( {h > 0} \right)\) . Đường sinh của hình nón bằng \(l = \sqrt {{h^2} + 4} \) Diện tích toàn phần của hình nón \({S_{tp}} = \pi .2.\sqrt {{h^2} + 4} + \pi {.2^2} = \pi \left( {2\sqrt {{h^2} + 4} + 4} \right)\,\,\left( {c{m^2}} \right)\) Vì chiều cao hình nón bằng đường kính hình cầu nên bán kính hình cầu là \(\dfrac{h}{2}\,\left( {cm} \right)\) Diện tích mặt cầu là \(S = 4\pi .{\left( {\dfrac{h}{2}} \right)^2} = \pi {h^2}\) Theo bài ra ta có \(\pi \left( {2\sqrt {{h^2} + 4} + 4} \right) = \pi {h^2}\) \(\begin{array}{l} \Leftrightarrow 2\sqrt {{h^2} + 4} + 4 = {h^2}\\ \Leftrightarrow 2\sqrt {{h^2} + 4} = {h^2} - 4\,\,\left( {h > 2} \right)\end{array}\) \(\begin{array}{l} \Rightarrow 4\left( {{h^2} + 4} \right) = {h^4} - 8{h^2} + 16\\ \Leftrightarrow {h^4} - 12{h^2} = 0\end{array}\) \( \Leftrightarrow \left[ \begin{array}{l}{h^2} = 0\\{h^2} = 12\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}h = 0\left( L \right)\\h = - 2\sqrt 3 \left( L \right)\\h = 2\sqrt 3 \,\left( N \right)\end{array} \right.\) Vậy chiều cao hình nón là \(2\sqrt 3 \,cm.\)
|
