Trắc nghiệm: Phép trừ hai số thập phân Toán 5Đề bài
Câu 1 :
A.
B. 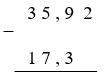 C. 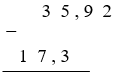 D.
Câu 2 :
Tính: \(42 - 18,37\) A. \(18,5\) B. \(23,37\) C. \(23,63\) D. \(24,37\)
Câu 3 :
\( 72,45 - 26,18 = ...\) A. \(57,27\) B. \(56,17\) C. \(46,27\) D. \(47,27\)
Câu 4 :
\( 51,2 - 17,83 = 33,43\). Đúng hay sai? Đúng Sai
Câu 5 :
Biết: \(49,5 - x = 27,83\). Vậy \(x = \)
Câu 6 :
Chọn dấu thích hợp để điền vào chỗ chấm: \(41,7 - 26,34\,\,\,...\,\,\,50 - 33,92\) A. \( =\) B. \( >\) C. \(< \)
Câu 7 :
Kéo thả dấu thích hợp vào ô trống:
\( = \)
\( > \)
\( < \)
\(75,8 - 13,46 - 26,54 \) ..... \( 75,8 - (13,46 + 26,54)\)
Câu 8 :
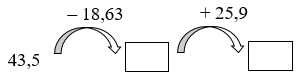 Số thích hợp điền vào ô trống từ trái sang phải lần lượt là: A. \( 24,93\) và \( 51,83\) B. \( 24,87\) và \( 50,77\) C. \(25,27 \) và \( 51,17\) D. \( 25,63\) và \( 51,53\)
Câu 9 :
Cho hình chữ nhật ABCD có chiều dài là \(34,82m\), chiều rộng ngắn hơn chiều dài \(6,9m.\) Vậy chiều rộng hình chữ nhật đó là \(m\).
Câu 10 :
\(82,25\)
\(82,55\)
\(85,25\)
\(85,55\)
\(45,27km + 23km\, \times \,4\, - 54,72km =\) ..... \(km.\)
Câu 11 :
\(136,78 - 52,49 + 13,22 - 47,51\) \( = (136,78 +\) \( ) - \,\,(52,49 + \) \( )\) \(=\) \(-\) \( =\)
Câu 12 :
Một thùng đựng $65kg$ đường. Người ta lấy ra từ thùng đó $23,5kg$ đường, sau đó lại lấy ra $8,75kg$ đường nữa. Hỏi trong thùng còn lại bao nhiêu ki-lô-gam đường? A. $33,75kg$ B. $32,25kg$ C. $32,75kg$ D. $41,5kg$
Câu 13 :
A. Tăng \(0,168\) đơn vị B. Giảm \(0,008\) đơn vị C. Giảm \(0,408\) đơn vị D. Tăng \(0,132\) đơn vị
Câu 14 :
Biết trung bình cộng của ba số là \(208\). Tổng của số thứ nhất và số thứ hai là \(442,45\). Tổng của số thứ hai và số thứ ba là \(426,8\). Hỏi trong ba số đã cho, số lớn nhất là số nào? A. Số thứ nhất B. Số thứ hai C. Số thứ ba Lời giải và đáp án
Câu 1 :
A.
B. 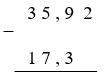C. 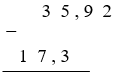D.
Đáp án
B. 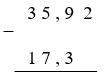Lời giải chi tiết :
Ta đặt tính như sau: - Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. - Viết dấu phẩy của số bị trừ và số trừ thẳng cột với nhau. Vậy trong các cách đặt tính đã cho chỉ có cách B là đúng quy tắc.
Câu 2 :
Tính: \(42 - 18,37\) A. \(18,5\) B. \(23,37\) C. \(23,63\) D. \(24,37\) Đáp án
C. \(23,63\) Phương pháp giải :
Đặt tính rồi tính theo quy tắc: - Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. (ta thấy số chữ số ở phần thập phân của số bị trừ ít hơn số chữ số ở phần thập phân của số trừ thì ta có thể viết thêm \(2\) chữ số \(0\) vào bên phải phần thập phân của số bị trừ) - Trừ như trừ các số tự nhiên. - Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ. Lời giải chi tiết :
Ta đặt tính và thực hiện tính như sau: \(\begin{array}{*{20}{c}}{ - \begin{array}{*{20}{c}}{42,00}\\{18,37}\end{array}}\\\hline{\,\,\,\,23,63}\end{array}\,\) Vậy: \( 42 - 18,37 = 23,63\).
Câu 3 :
\( 72,45 - 26,18 = ...\) A. \(57,27\) B. \(56,17\) C. \(46,27\) D. \(47,27\) Đáp án
C. \(46,27\) Phương pháp giải :
Muốn trừ một số thập phân cho một số thập phân ta làm như sau: - Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. - Trừ như trừ các số tự nhiên. - Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ. Lời giải chi tiết :
Ta đặt tính và thực hiện tính như sau: \(\begin{array}{*{20}{c}}{ - \begin{array}{*{20}{c}}{72,45}\\{26,18}\end{array}}\\\hline{\,\,\,46,27}\end{array}\) Vậy \( 72,45 - 26,18 = 46,27\).
Câu 4 :
\( 51,2 - 17,83 = 33,43\). Đúng hay sai? Đúng Sai Đáp án
Đúng Sai Phương pháp giải :
Muốn trừ một số thập phân cho một số thập phân ta làm như sau: - Viết số trừ dưới số bị trừ sao cho các chữ số ở cùng một hàng đặt thẳng cột với nhau. - Trừ như trừ các số tự nhiên. - Viết dấu phẩy ở hiệu thẳng cột với các dấu phẩy của số bị trừ và số trừ. Chú ý: Nếu số chữ số ở phần thập phân của số bị trừ ít hơn số chữ số ở phần thập phân của số trừ thì ta có thể viết thêm một số thích hợp chữ số \(0\) vào bên phải phần thập phân của số bị trừ rồi trừ như trừ các số tự nhiên. Lời giải chi tiết :
Ta đặt tính và thực hiện tính như sau: \(\begin{array}{*{20}{c}}{ - \begin{array}{*{20}{c}}{51,20}\\{17,83}\end{array}}\\\hline{\,\,\,\,33,37}\end{array}\) \( 51,2 - 17,83 = 33,37\). Do đó khẳng định \( 51,2 - 17,83 = 33,43\) là sai.
Câu 5 :
Biết: \(49,5 - x = 27,83\). Vậy \(x = \) Đáp án
Biết: \(49,5 - x = 27,83\). Vậy \(x = \) Phương pháp giải :
\(x\) ở vị trí số trừ nên để tìm \(x\) ta lấy số bị trừ trừ đi hiệu. Lời giải chi tiết :
\(\begin{array}{l}49,5-x = 27,83\\ \quad \quad\quad x = 49,5 - 27,83\\\quad\quad\quad x = 21,67\end{array}\) Vậy số thích hợp điền vào ô trống là \(21,67\).
Câu 6 :
Chọn dấu thích hợp để điền vào chỗ chấm: \(41,7 - 26,34\,\,\,...\,\,\,50 - 33,92\) A. \( =\) B. \( >\) C. \(< \) Đáp án
C. \(< \) Phương pháp giải :
Tính kết quả của từng vế rồi so sánh các kết quả với nhau. Lời giải chi tiết :
Ta có: \(41,7 - 26,34 = 15,36\,\,; \quad \quad \,\,\,50 - 33,92 = 16,08\) Mà \(15,36 < 16,08\). Vậy \(41,7 - 26,34\,\,\, < \,\,\,50 - 33,92\).
Câu 7 :
Kéo thả dấu thích hợp vào ô trống:
\( = \)
\( > \)
\( < \)
\(75,8 - 13,46 - 26,54 \) ..... \( 75,8 - (13,46 + 26,54)\) Đáp án
\( = \)
\( > \)
\( < \)
\(75,8 - 13,46 - 26,54 \)
\( = \) \( 75,8 - (13,46 + 26,54)\) Phương pháp giải :
Biểu thức vế trái chỉ có phép trừ, ta tính lần lượt từ trái qua phải. Biểu thức vế phải có chứa dấu ngoặc, ta tính trong ngoặc trước, ngoài ngoặc sau. Lời giải chi tiết :
Ta có: \(\begin{array}{l}+) \;75,8 - 13,46 - 26,54\,\, = 62,34\, - 26,54 = 35,8\\+) \; 75,8 - (13,46 + 26,54) = 75,8 - 40 = 35,8\end{array}\) Mà \(35,8 = 35,8\). Vậy \(75,8 - 13,46 - 26,54\,\, = \,75,8 - (13,46 + 26,54)\).
Câu 8 :
Số thích hợp điền vào ô trống từ trái sang phải lần lượt là: A. \( 24,93\) và \( 51,83\) B. \( 24,87\) và \( 50,77\) C. \(25,27 \) và \( 51,17\) D. \( 25,63\) và \( 51,53\) Đáp án
B. \( 24,87\) và \( 50,77\) Phương pháp giải :
- Ta tính lần lượt từ trái qua phải. - Áp dụng các quy tắc cộng hai số thập phân và trừ hai số thập phân. Lời giải chi tiết :
Tính lần lượt từ trái qua phải ta có: \(\begin{array}{l}43,5 - 18,63 = 24,87\\24,87 + 25,9 = 50,77\end{array}\) Vậy số thích hợp điền vào ô trống từ trái sang phải lần lượt là \(24,87\, ; \,\, 50,77\). Chọn B.
Câu 9 :
Cho hình chữ nhật ABCD có chiều dài là \(34,82m\), chiều rộng ngắn hơn chiều dài \(6,9m.\) Vậy chiều rộng hình chữ nhật đó là \(m\). Đáp án
Cho hình chữ nhật ABCD có chiều dài là \(34,82m\), chiều rộng ngắn hơn chiều dài \(6,9m.\) Vậy chiều rộng hình chữ nhật đó là \(m\). Phương pháp giải :
Chiều rộng ngắn hơn chiều dài \(6,9m\) nên chiều rộng bằng chiều dài trừ đi \(6,9m\). Lời giải chi tiết :
Chiều rộng hình chữ nhật đó là: \(34,82 - 6,9 = 27,92\; (m) \) Đáp số: \(27,92m \).
Câu 10 :
\(82,25\)
\(82,55\)
\(85,25\)
\(85,55\)
\(45,27km + 23km\, \times \,4\, - 54,72km =\) ..... \(km.\) Đáp án
\(82,25\)
\(82,55\)
\(85,25\)
\(85,55\)
\(45,27km + 23km\, \times \,4\, - 54,72km =\)
\(82,55\) \(km.\) Phương pháp giải :
- Biểu thức có chứa phép cộng, phép nhân và phép trừ nên ta thực hiện tính phép nhân trước, phép cộng, trừ sau. - Khi biểu thức chỉ có phép cộng, trừ thì ta tính lần lượt từ trái qua phải. Lời giải chi tiết :
Ta có: \(\begin{array}{l}45,27km + 23km \times \,4 - 54,72km\\ = 45,27km + 92km - 54,72km\\ = 137,27km - 54,72km\\ = 82,55km\end{array}\) Vậy số thích hợp điền vào ô trống là \(82,55\).
Câu 11 :
\(136,78 - 52,49 + 13,22 - 47,51\) \( = (136,78 +\) \( ) - \,\,(52,49 + \) \( )\) \(=\) \(-\) \( =\) Đáp án
\(136,78 - 52,49 + 13,22 - 47,51\) \( = (136,78 +\) \( ) - \,\,(52,49 + \) \( )\) \(=\) \(-\) \( =\) Phương pháp giải :
Ta có: $a -b + \,c - d\; = \;\left( {a + c} \right) - \left( {b + d} \right)$. Nhận thấy \(78 + 22 = 100;\,\,\,49 + 51 = 100\) nên ta nhóm các số thập phân có phần thập phân cộng với nhau là số tròn chục, tròn trăm, tròn nghìn, ... Lời giải chi tiết :
Ta có: \(\begin{array}{l}136,78 - 52,49 + 13,22 - 47,51\\ = (136,78 + 13,22) - (52,49 + 47,51)\\ = 150 - 100\\ = 50\end{array}\) Vậy số thích hợp điền vào ô trống từ trên xuống dưới, từ trái sang phải lần lượt là \(13,22 \,;\,\, 47,51 \,;\,\,150 \,;\,\,100\,;\,\, 50\).
Câu 12 :
Một thùng đựng $65kg$ đường. Người ta lấy ra từ thùng đó $23,5kg$ đường, sau đó lại lấy ra $8,75kg$ đường nữa. Hỏi trong thùng còn lại bao nhiêu ki-lô-gam đường? A. $33,75kg$ B. $32,25kg$ C. $32,75kg$ D. $41,5kg$ Đáp án
C. $32,75kg$ Phương pháp giải :
Để tìm được số đường còn lại trong thùng ta có thể làm như sau: Bước 1: Tìm số ki-lô-gam đường người ta đã lấy ra ta lấy số đường lấy lần thứ nhất cộng với số đường lấy lần thứ hai. Bước 2: Tìm số đường còn lại trong thùng ta lấy số đường có lúc đầu trừ đi số đường người ta lấy ra. Lời giải chi tiết :
Người ta đã lấy ra số ki-lô-gam đường là: $23,5 + 8,75 = 32,25\;(kg)$ Trong thùng còn lại số ki-lô-gam đường là: $65 - 32,25 = 32,75\;(kg)$ Đáp số: $32,75kg$.
Câu 13 :
A. Tăng \(0,168\) đơn vị B. Giảm \(0,008\) đơn vị C. Giảm \(0,408\) đơn vị D. Tăng \(0,132\) đơn vị Đáp án
D. Tăng \(0,132\) đơn vị Phương pháp giải :
- Xác định số mới sau khi xóa bỏ hai chữ số \(4\) và \(8\) ở phần thập phân của số $79,468$. - So sánh số ban đầu và số mới rồi tính xem tăng hay giảm bao nhiêu đơn vị. Lời giải chi tiết :
Số $79,468$ khi xóa bỏ hai chữ số \(4\) và \(8\) ở phần thập phân thì được số mới là \(79,6\). Ta có $79,468 < 79,6$. Số ban đầu sau khi xóa bỏ hai chữ số \(4\) và \(8\) ở phần thập phân đã tăng lên số đơn vị là: $79,6 - 79,468 = 0,132$
Câu 14 :
Biết trung bình cộng của ba số là \(208\). Tổng của số thứ nhất và số thứ hai là \(442,45\). Tổng của số thứ hai và số thứ ba là \(426,8\). Hỏi trong ba số đã cho, số lớn nhất là số nào? A. Số thứ nhất B. Số thứ hai C. Số thứ ba Đáp án
B. Số thứ hai Phương pháp giải :
- Nhớ lại công thức : tổng = trung bình cộng × số số hạng và áp dụng tìm tổng của ba số ta lấy trung bình cộng của ba số nhân với \(3\). - Tìm số thứ ba ta lấy tổng của ba số trừ đi tổng của số thứ nhất và số thứ hai. - Tìm số thứ hai ta lấy tổng của số thứ hai và số thứ ba trừ đi số thứ ba. - Tìm số thứ nhất ta lấy tổng của số thứ nhất và số thứ hai trừ đi số thứ hai. - So sánh ba số vừa tìm được để tìm số lớn nhất. Lời giải chi tiết :
Tổng của ba số đó là : \(208 \times 3 = 624\) Số thứ ba là: \(624 - 442,45 = 181,55\) Số thứ hai là: \(426,8 - 181,55 = 245,25\) Số thứ nhất là: \(442,45 - 245,25 = 197,2\) Ta có \(181,55 < 197,2 < 245,25\) nên số thứ hai là số lớn nhất trong ba số.
|
Cho phép tính \(35,92 - 17,3\). Tìm cách đặt tính đúng.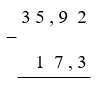
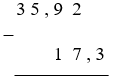
Chọn số thích hợp để điền vào chỗ chấm:
Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống:
Kéo thả số thích hợp vào ô trống:
Điền số thích hợp vào ô trống để tính bằng cách thuận tiện:
Cho số $79,468$. Hỏi số này thay đổi như thế nào nếu xóa bỏ hai chữ số \(4\) và \(8\) ở phần thập phân?
