Trắc nghiệm: Ôn tập chương 3 Toán 5Đề bài
Câu 1 :
Em hãy chọn phát biểu sai: A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). C. Muốn tính diện tích hình tròn ta lấy đường kính nhân với đường kính rồi nhân với số \(3,14\). D. Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\).
Câu 2 :
A. Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo). B. Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh. C. Cả A và B đều sai D. Cả A và B đều đúng
Câu 3 :
Điền số thích hợp vào ô trống: Cho hình thang có độ dài đáy lần lượt là $14cm$ và $18cm$; chiều cao là $11cm$. Diện tích hình thang đó là \(c{m^2}\).
Câu 4 :
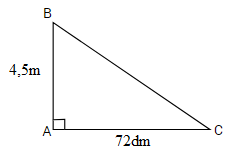
Điền số thích hợp vào ô trống: Cho tam giác ABC có số đo như hình vẽ:
Diện tích tam giác ABC là \(d{m^2}\).
Câu 5 :
Một hình chữ nhật có chu vi là \(32cm\) và chiều dài là \(9cm\). Tính chu vi hình tròn tâm \(O\) có bán kính bằng chiều rộng của hình chữ nhật. A. \(21,98cm\) B. \(43,96cm\) C. \(72,22cm\) D. \(144,44cm\)
Câu 6 :
Điền số thích hợp vào ô trống: Cho hình hộp chữ nhật có số đo như hình vẽ:
Vậy diện tích toàn phần của hình hộp chữ nhật đó là \(d{m^2}\).
Câu 7 :
Một hình lập phương có diện tích toàn phần là \(864c{m^2}\). Vậy diện tích xung quanh của hình lập phương đó là \(c{m^2}\).
Câu 8 :
Điền dấu thích hợp vào chỗ chấm: \(27,5{m^3}\) ... \(2750d{m^3}\) A. \( < \) B. \( > \) C. \( = \)
Câu 9 :
Cho hình hộp chữ nhật có thể tích bằng \(5,2d{m^3}\). Biết chiều dài là \(25cm\), chiều rộng là \(16cm\). Vậy diện tích xung quanh của hình hộp chữ nhật đó là \(c{m^2}\).
Câu 10 :
A. \(4\) lần B. \(16\) lần C. \(32\) lần D. \(64\) lần
Câu 11 :
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\). Vậy diện tích đáy căn phòng đó là \({m^2}\).
Câu 12 :
Một cái bể hình hộp chữ nhật có chiều dài là $2,5m$; chiều rộng kém chiều dài $1,3m$; chiều cao gấp $1,5$ lần chiều rộng. Hiện tại, lượng nước trong bể chiếm \(45\% \) thể tích của bể. Hỏi cần phải cho thêm vào bể bao nhiêu lít nước để được đầy bể nước? A. \(5400\) lít B. \(2970\) lít C. \(2700\) lít D. \(2430\) lít
Câu 13 :
Một bể nước dạng hình hộp chữ nhật có các kích thước đo ở trong lòng bể là: chiều dài là $1,5m$; chiều rộng $1,2m$, chiều cao \(2m\). Mặt nước cách miệng bể \(0,5m\). Người ta mở khóa cho nước chảy ra khỏi bể, sau \(5\) giờ thì bể cạn. Hỏi nước chảy ra khỏi bể mỗi phút được bao nhiêu lít? A. \(3\) lít B. \(6\) lít C. \(9\) lít D. \(12\) lít Lời giải và đáp án
Câu 1 :
Em hãy chọn phát biểu sai: A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). C. Muốn tính diện tích hình tròn ta lấy đường kính nhân với đường kính rồi nhân với số \(3,14\). D. Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\). Đáp án
C. Muốn tính diện tích hình tròn ta lấy đường kính nhân với đường kính rồi nhân với số \(3,14\). Phương pháp giải :
Dựa vào quy tắc tính diện tích các hình tam giác, hình thang, hình tròn và tính chu vi hình tròn. Lời giải chi tiết :
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). - Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2.\) - Muốn tính diện tích hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\). - Muốn tính chu vi hình tròn ta lấy đường kính nhân với số \(3,14\). Vậy kết luận sai là "Muốn tính diện tích hình tròn ta lấy đường kính nhân với đường kính rồi nhân với số \(3,14\)".
Câu 2 :
A. Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo). B. Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh. C. Cả A và B đều sai D. Cả A và B đều đúng Đáp án
D. Cả A và B đều đúng Phương pháp giải :
Dựa vào quy tắc tính thể tích hình lập phương và hình hộp chữ nhật. Lời giải chi tiết :
- Muốn tính thể tích hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng đơn vị đo). - Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh. Vậy cả A và B đều đúng
Câu 3 :
Điền số thích hợp vào ô trống: Cho hình thang có độ dài đáy lần lượt là $14cm$ và $18cm$; chiều cao là $11cm$. Diện tích hình thang đó là \(c{m^2}\). Đáp án
Cho hình thang có độ dài đáy lần lượt là $14cm$ và $18cm$; chiều cao là $11cm$. Diện tích hình thang đó là \(c{m^2}\). Phương pháp giải :
Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). Lời giải chi tiết :
Diện tích hình thang đã cho là: \((14 + 18) \times 11:2 = 176\;(c{m^2})\) Đáp số: \(176c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(176\).
Câu 4 :
Điền số thích hợp vào ô trống: Cho tam giác ABC có số đo như hình vẽ:
Diện tích tam giác ABC là \(d{m^2}\). Đáp án
Cho tam giác ABC có số đo như hình vẽ:
Diện tích tam giác ABC là \(d{m^2}\). Phương pháp giải :
- Đổi độ dài hai cạnh góc vuông về cùng một đơn vị đo là đề-xi-mét. - Tính diện tích tam giác vuông ta tìm tích độ dài hai cạnh góc vuông rồi chia cho \(2\). Lời giải chi tiết :
Đổi \(4,5m = 45dm\) Diện tích tam giác \(ABC\) là: \(45 \times 72:2 = 1620 \; (d{m^2})\) Đáp số: \(1620d{m^2}\). Vậy đáp án đúng điền vào ô trống là \(1620\).
Câu 5 :
Một hình chữ nhật có chu vi là \(32cm\) và chiều dài là \(9cm\). Tính chu vi hình tròn tâm \(O\) có bán kính bằng chiều rộng của hình chữ nhật. A. \(21,98cm\) B. \(43,96cm\) C. \(72,22cm\) D. \(144,44cm\) Đáp án
B. \(43,96cm\) Phương pháp giải :
- Tính nửa chu vi hình chữ nhật : nửa chu vi = chu vi : 2. - Tính chiều rộng hình chữ nhật: chiều rộng = nửa chu vi – chiều dài. - Hình tròn tâm \(O\) có bán kính bằng chiều rộng của hình chữ nhật nên ta tìm được bán kính của hình tròn. - Tính chu vi hình tròn ta lấy \(2\) lần bán kính nhân với số \(3,14\). Lời giải chi tiết :
Nửa chu vi hình chữ nhật là: \(32:2 = 16 \;(cm)\) Chiều rộng hình chữ nhật: \(16 - 9 = 7\;(cm)\) Hình tròn tâm \(O\) có bán kính bằng chiều rộng của hình chữ nhật nên bán kính của hình tròn là \(7cm\). Chu vi hình tròn là: \(7 \times 2 \times 3,14 = 43,96\;(cm)\) Đáp số: \(43,96cm\).
Câu 6 :
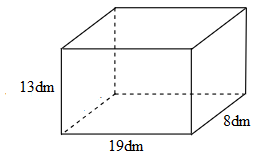
Điền số thích hợp vào ô trống: Cho hình hộp chữ nhật có số đo như hình vẽ:
Vậy diện tích toàn phần của hình hộp chữ nhật đó là \(d{m^2}\). Đáp án
Cho hình hộp chữ nhật có số đo như hình vẽ:
Vậy diện tích toàn phần của hình hộp chữ nhật đó là \(d{m^2}\). Phương pháp giải :
Hình hộp chữ nhật đã cho có chiều dài \(19dm\), chiều rộng \(8dm\) và chiều cao \(13dm\). Để giải bài này ta có thể làm như sau: - Tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao. - Tính diện tích đáy ta lấy chiều dài nhân với chiều rộng. - Tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy. Lời giải chi tiết :
Diện tích xung quanh của hình hộp chữ nhật là: \((19 + 8) \times 2 \times 13 = 702\;(d{m^2})\) Diện tích đáy của hình hộp chữ nhật là: \(19 \times 8 = 152\;(d{m^2})\) Diện tích toàn phần của hình hộp chữ nhật là: \(702 + 152 \times 2 = 1006\;(d{m^2})\) Đáp số: \(1006d{m^2}\). Vậy đáp án đúng điền vào ô trống là \(1006\).
Câu 7 :
Một hình lập phương có diện tích toàn phần là \(864c{m^2}\). Vậy diện tích xung quanh của hình lập phương đó là \(c{m^2}\). Đáp án
Một hình lập phương có diện tích toàn phần là \(864c{m^2}\). Vậy diện tích xung quanh của hình lập phương đó là \(c{m^2}\). Phương pháp giải :
- Diện tích toàn phần \(=\) diện tích $1$ mặt \( \times \,6\) nên diện tích $1$ mặt \(=\) diện tích toàn phần \(:6\). - Diện tích xung quanh \(=\) diện tích $1$ mặt \( \times \,4\). Lời giải chi tiết :
Diện tích một mặt của hình lập phương đó là: \(864:6 = 144\;(c{m^2})\) Diện tích xung quanh của hình lập phương đó là: \(144 \times 4 = 576\;(c{m^2})\) Đáp số: \(576c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(576\).
Câu 8 :
Điền dấu thích hợp vào chỗ chấm: \(27,5{m^3}\) ... \(2750d{m^3}\) A. \( < \) B. \( > \) C. \( = \) Đáp án
B. \( > \) Phương pháp giải :
Áp dụng cách đổi \(1{m^3} = 1000d{m^3}\) để đổi hai số đo về cùng một đơn vị đo rồi so sánh kết quả.
Lời giải chi tiết :
Ta có: \(1{m^3} = 1000d{m^3}\) và \(27,5 \times 1000 = 27500\) nên \(27,5{m^3} = 27500d{m^3}\). Mà \(27500d{m^3} > 2750d{m^3}\). Vậy \(27,5{m^3} > 2750d{m^3}\).
Câu 9 :
Cho hình hộp chữ nhật có thể tích bằng \(5,2d{m^3}\). Biết chiều dài là \(25cm\), chiều rộng là \(16cm\). Vậy diện tích xung quanh của hình hộp chữ nhật đó là \(c{m^2}\). Đáp án
Cho hình hộp chữ nhật có thể tích bằng \(5,2d{m^3}\). Biết chiều dài là \(25cm\), chiều rộng là \(16cm\). Vậy diện tích xung quanh của hình hộp chữ nhật đó là \(c{m^2}\). Phương pháp giải :
Thể tích của hình hộp chữ nhật = Chiều dài × chiều rộng × chiều cao = Diện tích đáy × chiều cao. Do đó, Chiều cao = Thể tích của hình hộp chữ nhật : diện tích đáy (chú ý : đơn vị phải tương ứng với nhau, ví dụ các kích thước của hình có đơn vị là xăng-ti-mét thì thể tích có đơn vị xăng-ti-mét khối). Để giải bài này ta có thể thực hiện như sau: - Đổi \(5,2d{m^3} = 5200c{m^3}\) - Tính diện tích đáy ta lấy chiều dài nhân với chiều rộng. - Tính chiều cao ta lấy thể tích của hình hộp chữ nhật chia cho diện tích đáy. - Tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi đáy nhân với chiều cao. Lời giải chi tiết :
Đổi \(5,2d{m^3} = 5200c{m^3}\) Diện tích mặt đáy của hình hộp chữ nhật đó là: \(25 \times 16 = 400 \;(c{m^2})\) Chiều cao của hình hộp chữ nhật đó là: \(5200:400 = 13\;(cm)\) Diện tích xung quanh của hình hộp chữ nhật đó là: \((25 + 16) \times 2 \times 13 = 1066 \; (c{m^2})\) Đáp số: \(1066c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(1066\).
Câu 10 :
A. \(4\) lần B. \(16\) lần C. \(32\) lần D. \(64\) lần Đáp án
D. \(64\) lần Phương pháp giải :
- Giả sử cạnh hình lập phương B là \(a\) thì cạnh hình lập phương A là \(4 \times a\). - Tính thể tích hai hình lập phương đó rồi so sánh. Thể tích hình lập phương = cạnh \(\times \) cạnh \(\times \) cạnh. Lời giải chi tiết :
Giả sử cạnh hình lập phương B là \(a\) thì cạnh hình lập phương A là \(4 \times a\). Thể tích hình lập phương B là ${V_{(B)}} = a \times a \times a$ Thể tích hình lập phương A là: ${V_{(A)}} = (4 \times a) \times (4 \times a) \times (4 \times a) $ $= (4 \times 4 \times 4) \times (a \times a \times a) $ $= 64 \times (a \times a \times a) $ $= 64 \times {V_{(B)}}$ Vậy nếu hình lập phương A có độ cạnh dài gấp \(4\) lần cạnh hình lập phương B thì thể tích hình A gấp \(64\) lần thể tích hình B.
Câu 11 :
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\). Vậy diện tích đáy căn phòng đó là \({m^2}\). Đáp án
Một căn phòng hình hộp chữ nhật chứa được \(36\) người và mỗi người có đủ \(4,5{m^3}\) không khí để thở. Biết chiều cao căn phòng là \(4m\). Vậy diện tích đáy căn phòng đó là \({m^2}\). Phương pháp giải :
Thể tích không khí chứa trong phòng chính bằng thể tích của căn phòng đó. Để giải bài này ta có thể làm như sau: - Tìm thể tích không khí ta lấy số mét khối không khí để thở của một người nhân với số người. Từ đó tìm được thể tích căn phòng. - Tìm diện tích đáy của căn phòng ta lấy thể tích chia cho chiều cao. Lời giải chi tiết :
Thể tích không khí chứa trong phòng là: \(4,5 \times 36 = 162 \;({m^3})\) Diện tích đáy căn phòng đó là: \(162:4 = 40,5 \;({m^2})\) Đáp số: \(40,5{m^2}\). Vậy đáp án đúng điền vào ô trống là \(40,5\).
Câu 12 :
Một cái bể hình hộp chữ nhật có chiều dài là $2,5m$; chiều rộng kém chiều dài $1,3m$; chiều cao gấp $1,5$ lần chiều rộng. Hiện tại, lượng nước trong bể chiếm \(45\% \) thể tích của bể. Hỏi cần phải cho thêm vào bể bao nhiêu lít nước để được đầy bể nước? A. \(5400\) lít B. \(2970\) lít C. \(2700\) lít D. \(2430\) lít Đáp án
B. \(2970\) lít Phương pháp giải :
Thể tích nước khi bể đầy nước chính là thể thể tích của hình hộp chữ nhật có chiều dài $2,5m$ ; chiều rộng kém chiều dài $1,3m$ và chiều cao gấp $1,5$ chiều rộng. Để giải bài ta có thể làm như sau: - Tính chiều rộng ta lấy chiều dài trừ đi \(1,3m\). - Tính chiều cao ta lấy chiều rộng nhân với \(1,5\). - Tính thể tích bể nước đó theo công thức: Thể tích = Chiều dài × chiều rộng × chiều cao. - Tính thể tích nước đang có trong bể, tức là tìm \(45\% \) thể tích bể ta lấy thể tích bể nước chia cho \(100\) nhân với \(45\). - Tính thể tích cần đổ thêm vào bể ta lấy thể tích bể nước trừ đi thể tích nước đang có trong bể. - Đổi thể tích từ đơn vị mét khối sang đơn vị đề-xi-mét khối rồi tính số lít nước. Lời giải chi tiết :
Chiều rộng của bể nước là: $2,5 - 1,3 = 1,2 \;(m)$ Chiều cao của bể nước là: $1,2 \times 1,5 = 1,8\;(m)$ Thể tích của bể nước là: \(2,5 \times 1,2 \times 1,8 = 5,4\;({m^3})\) Thể tích nước đang có trong bể là: \(5,4:100 \times 45 = 2,43\;({m^3})\) Thể tích cần đổ thêm vào bể để bể đầy nước là: \(5,4 - 2,43 = 2,97\;({m^3})\) Đổi \(2,97{m^3} = 2970d{m^3} = 2970\) lít Đáp số: \(2970\) lít.
Câu 13 :
Một bể nước dạng hình hộp chữ nhật có các kích thước đo ở trong lòng bể là: chiều dài là $1,5m$; chiều rộng $1,2m$, chiều cao \(2m\). Mặt nước cách miệng bể \(0,5m\). Người ta mở khóa cho nước chảy ra khỏi bể, sau \(5\) giờ thì bể cạn. Hỏi nước chảy ra khỏi bể mỗi phút được bao nhiêu lít? A. \(3\) lít B. \(6\) lít C. \(9\) lít D. \(12\) lít Đáp án
C. \(9\) lít Phương pháp giải :
- Vì mặt nước cách miệng bể \(0,5m\) nên tính chiều cao mực nước trong bể ta lấy chiều cao của bể trừ đi \(0,5m\). - Tính thể tích nước đang có trong bể ta lấy chiều dài nhân chiều rộng rồi nhân với chiều cao mực nước. - Tính thể tích nước chảy ra trong \(1\) giờ ta lấy thể tích nước chia cho 5. - Đổi thể tích nước chảy ra trong \(1\) giờ sang đơn vị đề-xi-mét khối, từ đó tìm được số lít nước chảy ra trong \(1\) giờ. - Đổi \(1\) giờ $ = 60$ phút. Để tìm số lít nước chảy ra trong \(1\) phút ta lấy số lít nước chảy ra trong \(1\) giờ chia cho \(60\). Lời giải chi tiết :
Chiều cao mực nước trong bể là: \(2 - 0,5 = 1,5\;(m)\) Thể tích nước đang có trong bể \(1,5 \times 1,2 \times 1,5 = 2,7\;({m^3})\) Thể tích nước chảy ra trong \(1\) giờ là: \(2,7:5 = 0,54\;({m^3})\) Đổi \(0,54{m^3} = 540d{m^3} = 540\) lít; \(1\) giờ $ = 60$ phút Mỗi phút nước chảy ra khỏi bể số lít là: \(540:60 = 9\) (lít) Đáp số: \(9\) lít.
|
