Trắc nghiệm: Hai vật chuyển động ngược chiều Toán 5Đề bài
Câu 1 :
Một ô tô đi từ A đến B với vận tốc là \({v_1}\), cùng lúc đó xe máy đi từ B đến A với vận tốc là \({v_2}\). Độ dài quãng đường AB là \(s\). Công thức tính thời gian đi để hai xe gặp nhau là: A. \({t_{gn}} = s:({v_1} + {v_2})\) B. \({t_{gn}} = s:({v_1} - {v_2})\) C. \({t_{gn}} = s:({v_1} \times {v_2})\) D. \({t_{gn}} = s:({v_1}:{v_2})\)
Câu 2 :
Quãng đường AB dài $360km$. Một ô tô đi từ A tới B với vận tốc $50$ km/giờ. Cùng lúc đó một xe máy đi từ B tới A với vận tốc $40$ km/giờ. Hỏi sau bao lâu hai xe gặp nhau? A. \(0,18\) giờ B. \(4\) giờ C. \(36\) giờ D. \(288\) giờ
Câu 3 :
Hai ca nô khởi hành cùng một lúc, đi ngược chiều nhau trên quãng đường sông AB dài $153km$. Vận tốc của ca nô đi từ A đến B là \(36\) km/giờ và hơn vận tốc ca nô đi từ B đến A là \(4\) km/giờ. Hỏi kể từ khi khởi hành, sau bao lâu hai ca nô gặp nhau? A. \(2,25\) giờ B. \(3,825\) giờ C. \(4,78\) giờ D. \(38,25\) giờ
Câu 4 :
Điền số thích hợp vào ô trống: Quãng đường từ Hà Nội đến Hải Dương dài $90km$. Lúc \(7\) giờ \(15\) phút, anh Tuấn đi từ Hà Nội về Hải Dương với vận tốc \(35\) km/giờ. Cùng lúc đó anh Huy cũng đi từ Hải Dương lên Hà Nội với vận tốc $40$ km/giờ. Vậy hai người gặp nhau lúc giờ phút.
Câu 5 :
Hai thành phố A và B cách nhau $135km$. Một xe máy đi từ A đến B với vận tốc $42$ km/giờ và một xe đạp đi từ B đến A với vận tốc $12$ km/giờ. Hỏi sau bao lâu hai xe gặp nhau? Lúc gặp nhau xe máy cách B bao nhiêu ki-lô-mét? A. \(4,5\) giờ; \(81km\) B. \(2,5\) giờ; \(105km\) C. \(4,5\) giờ; \(54km\) D. \(2,5\) giờ; \(30km\)
Câu 6 :
Điền số thích hợp vào ô trống: Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau. Vậy quãng đường từ thị xã A đến thị xã B dài \(km\).
Câu 7 :
Điền số thích hợp vào ô trống: Quãng đường AB dài $126km$. Cùng một lúc ô tô đi từ A tới B, xe máy đi từ B tới A. Sau \(1\) giờ \(45\) phút thì hai xe gặp nhau. Biết rằng vận tốc xe máy bằng \(\dfrac{3}{5}\) vận tốc của ô tô. Vậy vận tốc ô tô là km/giờ; vận tốc xe máy là km/giờ.
Câu 8 :
Cùng một lúc, một ô tô đi từ tỉnh A đến tỉnh B với vận tốc lớn hơn vận tốc xe máy đi từ tỉnh B đến tỉnh A là $15$km/giờ. Sau \(2\) giờ ô tô và xe máy gặp nhau. Khoảng cách từ tỉnh A đến tỉnh B là $150km$. Tính vận tốc mỗi xe. A. Ô tô : \(48\) km/giờ; xe máy: \(33\) km/giờ B. Ô tô : \(45\) km/giờ; xe máy: \(30\) km/giờ C. Ô tô : \(55\) km/giờ; xe máy: \(40\) km/giờ D. Ô tô : \(60\) km/giờ; xe máy: \(45\) km/giờ
Câu 9 :
Một ô tô đi từ tỉnh A đến tỉnh B với vận tốc $54$ km/giờ. Ô tô đi được $40$ phút thì có một xe máy đi từ B đến A với vận tốc $36$ km/giờ. Biết quãng đường AB dài $81km$ . Hỏi sau bao lâu kể từ khi xe máy xuất phát thì hai xe gặp nhau? Chỗ gặp nhau cách B bao nhiêu ki-lô-mét? A. \(0,9\) giờ; \(32,4km\) B. \(0,66\) giờ; \(23,76km\) C. \(2,5\) giờ; \(18km\) D. \(0,5\) giờ; \(18km\)
Câu 10 :
Điền số thích hợp vào ô trống: Lúc \(8\) giờ $30$ phút ô tô thứ nhất đi từ A đến B với vận tốc $44$ km/giờ. Lúc $9$ giờ ô tô thứ hai đi từ B để đến A với vận tốc $56$ km/giờ. Hai xe gặp nhau lúc $10$ giờ $45$ phút. Vậy độ dài quãng đường AB là \(km\).
Câu 11 :
Lúc \(7\) giờ, xe thứ nhất đi từ A đến B với vận tốc $40$ km/giờ. Đến \(7\) giờ \(45\) phút, xe thứ hai đi từ B đến A. Đến \(9\) giờ hai xe gặp nhau. Hỏi xe thứ hai đi với vận tốc bao nhiêu, biết rằng quãng đường AB dài $142,5km$. A. \(16,25\) km/giờ B. \(31,25\) km/giờ C. \(50\) km/giờ D. \(74\) km/giờ Lời giải và đáp án
Câu 1 :
Một ô tô đi từ A đến B với vận tốc là \({v_1}\), cùng lúc đó xe máy đi từ B đến A với vận tốc là \({v_2}\). Độ dài quãng đường AB là \(s\). Công thức tính thời gian đi để hai xe gặp nhau là: A. \({t_{gn}} = s:({v_1} + {v_2})\) B. \({t_{gn}} = s:({v_1} - {v_2})\) C. \({t_{gn}} = s:({v_1} \times {v_2})\) D. \({t_{gn}} = s:({v_1}:{v_2})\) Đáp án
A. \({t_{gn}} = s:({v_1} + {v_2})\) Phương pháp giải :
Hai vật xuất phát cùng lúc, thời gian đi để gặp nhau bằng quãng đường chia cho tổng hai vận tốc. Lời giải chi tiết :
Theo đề bài, ô tô và xe máy xuất phát cùng lúc, thời gian đi để gặp nhau bằng quãng đường chia cho tổng hai vận tốc, hay \({t_{gn}} = s:({v_1} + {v_2})\).
Câu 2 :
Quãng đường AB dài $360km$. Một ô tô đi từ A tới B với vận tốc $50$ km/giờ. Cùng lúc đó một xe máy đi từ B tới A với vận tốc $40$ km/giờ. Hỏi sau bao lâu hai xe gặp nhau? A. \(0,18\) giờ B. \(4\) giờ C. \(36\) giờ D. \(288\) giờ Đáp án
B. \(4\) giờ Phương pháp giải :
Theo đề bài, ô tô và xe máy xuất phát cùng lúc. Để giải bài này ta làm như sau: - Tính tổng vận tốc hai xe. - Thời gian đi để gặp nhau bằng quãng đường chia cho tổng hai vận tốc. Lời giải chi tiết :
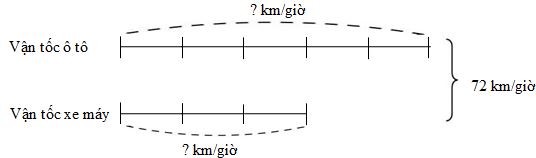
Ta có sơ đồ chuyển động của hai xe như sau:
Tổng vận tốc của hai xe là: \(50 + 40 = 90\) (km/giờ) Thời gian đi để hai xe gặp nhau là: \(360:90 = 4\) (giờ) Đáp số: \(4\) giờ. Chú ý
Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách lấy quãng đường chia cho hiệu hai vận tốc.
Câu 3 :
Hai ca nô khởi hành cùng một lúc, đi ngược chiều nhau trên quãng đường sông AB dài $153km$. Vận tốc của ca nô đi từ A đến B là \(36\) km/giờ và hơn vận tốc ca nô đi từ B đến A là \(4\) km/giờ. Hỏi kể từ khi khởi hành, sau bao lâu hai ca nô gặp nhau? A. \(2,25\) giờ B. \(3,825\) giờ C. \(4,78\) giờ D. \(38,25\) giờ Đáp án
A. \(2,25\) giờ Phương pháp giải :
- Tính vận tốc của ca nô đi từ B ta lấy vận tốc ca nô đi từ A trừ đi \( \,4\) km/giờ. - Tính tổng vận tốc hai xe. - Thời gian đi để gặp nhau = quãng đường : tổng vận tốc hai xe. Lời giải chi tiết :
Vận tốc của ca nô đi từ B đến A là: \(36 - 4 = 32\) (km/giờ) Tổng vận tốc hai ca nô là: \(36 + 32 = 68\) (km/giờ) Kể từ khi khởi hành, hai ca nô gặp nhau sau khi đi số giờ là: \(153:68 = 2,25\) (giờ) Đáp số: \(2,25\) giờ. Chú ý
- Học sinh có thể làm sai khi xác định vận tốc ca nô đi từ B là \(4\) km/giờ, sau đó tính thời gian đi để gặp nhau bằng cách lấy quãng đường chia cho tổng hai vận tốc hoặc chia cho hiệu hai vận tốc. Từ đó dẫn đến đáp án sai là B hoặc C. - Học sinh tính đúng vận tốc ca nô đi từ B nhưng có thể làm sai khi tính thời gian đi để gặp nhau bằng cách lấy quãng đường chia cho hiệu hai vận tốc. Từ đó dẫn đến đáp án sai là D.
Câu 4 :
Điền số thích hợp vào ô trống: Quãng đường từ Hà Nội đến Hải Dương dài $90km$. Lúc \(7\) giờ \(15\) phút, anh Tuấn đi từ Hà Nội về Hải Dương với vận tốc \(35\) km/giờ. Cùng lúc đó anh Huy cũng đi từ Hải Dương lên Hà Nội với vận tốc $40$ km/giờ. Vậy hai người gặp nhau lúc giờ phút. Đáp án
Quãng đường từ Hà Nội đến Hải Dương dài $90km$. Lúc \(7\) giờ \(15\) phút, anh Tuấn đi từ Hà Nội về Hải Dương với vận tốc \(35\) km/giờ. Cùng lúc đó anh Huy cũng đi từ Hải Dương lên Hà Nội với vận tốc $40$ km/giờ. Vậy hai người gặp nhau lúc giờ phút. Phương pháp giải :
Theo đề bài, hai người xuất phát cùng lúc. Để giải bài này ta làm như sau: - Tính tổng vận tốc hai xe. - Thời gian đi để gặp nhau = quãng đường : tổng vận tốc hai xe. - Đổi số đo thời gian dạng số thập phân sang dạng số tự nhiên. - Thời gian lúc hai người gặp nhau = thời gian xuất phát + thời gian đi để gặp nhau. Lời giải chi tiết :
Tổng vận tốc của hai anh là: \(35 + 40 = 75\) (km/giờ) Thời gian đi để hai anh gặp nhau là: \(90:75 = 1,2\) (giờ) Đổi \(1,2\) giờ \( = \,\,72\) phút \( = \,\,1\) giờ \(12\) phút Hai người gặp nhau lúc: \(7\) giờ \(15\) phút \( + \,\,1\) giờ \(12\) phút \( = \,\,8\) giờ \(27\) phút Đáp số: \(8\) giờ \(27\) phút. Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(8\,;\,\,27\). Chú ý
- Học sinh có thể làm sai khi xác định thời gian lúc hai người gặp nhau chính là thời gian đi để gặp nhau (tức là gặp nhau lúc \(1\) giờ \(12\) phút). - Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách lấy quãng đường chia cho hiệu vận tốc.
Câu 5 :
Hai thành phố A và B cách nhau $135km$. Một xe máy đi từ A đến B với vận tốc $42$ km/giờ và một xe đạp đi từ B đến A với vận tốc $12$ km/giờ. Hỏi sau bao lâu hai xe gặp nhau? Lúc gặp nhau xe máy cách B bao nhiêu ki-lô-mét? A. \(4,5\) giờ; \(81km\) B. \(2,5\) giờ; \(105km\) C. \(4,5\) giờ; \(54km\) D. \(2,5\) giờ; \(30km\) Đáp án
D. \(2,5\) giờ; \(30km\) Phương pháp giải :
Theo đề bài, xe đạp và xe máy xuất phát cùng lúc. Để giải bài này ta làm như sau: - Tính tổng vận tốc hai xe. - Thời gian đi để gặp nhau = quãng đường : tổng vận tốc hai xe. - Khoảng cách từ chỗ gặp nhau đến B chính là quãng đường mà xe đạp đã đi từ lúc xuất phát đến lúc gặp nhau. Để tính quãng đường đó ta lấy vận tốc xe đạp nhân với thời gian đi để gặp nhau. Cách giải: Lời giải chi tiết :
Tổng vận tốc của hai xe là: \(42 + 12 = 54\) (km/giờ) Thời gian đi để hai xe gặp nhau là: \(135:54 = 2,5\) (giờ) Chỗ gặp nhau cách B số ki-lô-mét là: \(12 \times 2,5 = 30 \;(km)\) Đáp số: \(2,5\) giờ; \(30km\). Chú ý
- Học sinh có thể sai khi xác định khoảng cách từ chỗ gặp nhau đến B là quãng đường mà xe máy đã đi từ lúc xuất phát đến lúc gặp nhau. Từ đó chọn đáp án sai là B. - Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách lấy quãng đường chia cho hiệu vận tốc. Từ đó tìm khoảng cách từ chỗ gặp nhau đến B là \(54km\) và chọn đáp án sai là C. - Có thể tìm khoảng cách từ chỗ gặp nhau đến B bằng cách lấy độ dài quãng đường AB trừ đi khoảng cách từ chỗ gặp nhau đến A.
Câu 6 :
Điền số thích hợp vào ô trống: Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau. Vậy quãng đường từ thị xã A đến thị xã B dài \(km\). Đáp án
Một ô tô đi từ thị xã A đến thị xã B với vận tốc là $48$ km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc $54$ km/giờ. Sau \(2\) giờ \(30\) phút hai ô tô gặp nhau. Vậy quãng đường từ thị xã A đến thị xã B dài \(km\). Phương pháp giải :
Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau: - Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ. - Tính tổng vận tốc hai ô tô. - Tính quãng đường ta lấy tổng hai vận tốc nhân với thời gian đi để gặp nhau. Lời giải chi tiết :
Đổi: \(2\) giờ \(30\) phút \( = \,\,2,5\) giờ Tổng vận tốc hai ô tô là: \(48 + 54 = 102\) (km/giờ) Quãng đường từ thị xã A đến thị xã B dài số ki-lô-mét là: \(102 \times 2,5 = 255 \;(km)\) Đáp số: \(255km\). Vậy đáp án đúng điền vào ô trống là \(255\).
Câu 7 :
Điền số thích hợp vào ô trống: Quãng đường AB dài $126km$. Cùng một lúc ô tô đi từ A tới B, xe máy đi từ B tới A. Sau \(1\) giờ \(45\) phút thì hai xe gặp nhau. Biết rằng vận tốc xe máy bằng \(\dfrac{3}{5}\) vận tốc của ô tô. Vậy vận tốc ô tô là km/giờ; vận tốc xe máy là km/giờ. Đáp án
Quãng đường AB dài $126km$. Cùng một lúc ô tô đi từ A tới B, xe máy đi từ B tới A. Sau \(1\) giờ \(45\) phút thì hai xe gặp nhau. Biết rằng vận tốc xe máy bằng \(\dfrac{3}{5}\) vận tốc của ô tô. Vậy vận tốc ô tô là km/giờ; vận tốc xe máy là km/giờ. Phương pháp giải :
Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau: - Đổi số đo thời gian sang dạng số thập phân có đơn vị là giờ. - Tính tổng vận tốc hai ô tô ta lấy quãng đường chia cho thời gian đi để gặp nhau. - Khi đó ta có bài toán tìm hai số khi biết tổng và tỉ số. Theo đề bài, vận tốc xe máy bằng \(\dfrac{3}{5}\) vận tốc của ô tô nên ta vẽ sơ đồ biểu thị vận tốc xe máy là \(3\) phần thì vận tốc ô tô là \(5\) phần như thế. Cọi vận tốc xe máy là số bé, vận tốc ô tô là số lớn, ta tìm hai số theo công thức: Số bé = Giá trị một phần × số phần của số bé hoặc Số lớn = Giá trị một phần × số phần của số lớn. Lời giải chi tiết :
Đổi \(1\) giờ \(45\) phút \( = \,1,75\) giờ Tổng vận tốc hai xe là: \(126:1,75 = 72\) (km/giờ) Ta có sơ đồ:
Tổng số phần bằng nhau là: \(3 + 5 = 8\) (phần) Vận tốc ô tô là: \(72:8 \times 5 = 45\) (km/giờ) Vận tốc xe máy là \(72 - 45 = 27\) (km/giờ) Đáp số: Vận tốc ô tô: \(45\) km/giờ; Vận tốc xe máy \(27\) km/giờ. Vậy đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(45\,;\,\,27\). Chú ý
Học sinh có thể đổi sai số đo thời gian sang dạng số thập phân có đơn vị là giờ nên tìm tổng vận tốc chưa đúng, từ đó tìm vận tốc mỗi xe cũng sẽ chưa đúng.
Câu 8 :
Cùng một lúc, một ô tô đi từ tỉnh A đến tỉnh B với vận tốc lớn hơn vận tốc xe máy đi từ tỉnh B đến tỉnh A là $15$km/giờ. Sau \(2\) giờ ô tô và xe máy gặp nhau. Khoảng cách từ tỉnh A đến tỉnh B là $150km$. Tính vận tốc mỗi xe. A. Ô tô : \(48\) km/giờ; xe máy: \(33\) km/giờ B. Ô tô : \(45\) km/giờ; xe máy: \(30\) km/giờ C. Ô tô : \(55\) km/giờ; xe máy: \(40\) km/giờ D. Ô tô : \(60\) km/giờ; xe máy: \(45\) km/giờ Đáp án
B. Ô tô : \(45\) km/giờ; xe máy: \(30\) km/giờ Phương pháp giải :
Theo đề bài, hai ô tô xuất phát cùng lúc. Để giải bài này ta làm như sau: - Tính tổng vận tốc hai ô tô ta lấy quãng đường chia cho thời gian đi để gặp nhau. - Khi đó ta có bài toán tìm hai số khi biết tổng và hiệu của hai số đó. Coi vận tốc xe máy là số bé và vận tốc ô tô là số lớn, ta tìm hai số theo công thức: Số bé = (tổng – hiệu) : \(2\) ; Số lớn = (tổng + hiệu) : \(2\) Lời giải chi tiết :
Tổng vận tốc hai xe là: \(150:2 = 75\) (km/giờ) Vận tốc ô tô là: \((75 + 15):2 = 45\) (km/giờ) Vận tốc xe máy là: \(45 - 15 = 30\) (km/giờ) Đáp số: Ô tô : \(45\) km/giờ; Xe máy: \(30\) km/giờ. Chú ý
Học sinh cần nhớ cách giải bài toán tìm hai số khi biết tổng và hiệu của hai số đó. Hoc sinh có thể làm sai khi tìm số lớn bằng cách lấy tổng trừ đi hiệu và chọn đáp sai là D.
Câu 9 :
Một ô tô đi từ tỉnh A đến tỉnh B với vận tốc $54$ km/giờ. Ô tô đi được $40$ phút thì có một xe máy đi từ B đến A với vận tốc $36$ km/giờ. Biết quãng đường AB dài $81km$ . Hỏi sau bao lâu kể từ khi xe máy xuất phát thì hai xe gặp nhau? Chỗ gặp nhau cách B bao nhiêu ki-lô-mét? A. \(0,9\) giờ; \(32,4km\) B. \(0,66\) giờ; \(23,76km\) C. \(2,5\) giờ; \(18km\) D. \(0,5\) giờ; \(18km\) Đáp án
D. \(0,5\) giờ; \(18km\) Phương pháp giải :
Theo đề bài, xe đạp và xe máy xuất phát không cùng lúc. Sau khi ô tô đã đi được $40$ phút thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau: - Đổi $40$ phút \( = \dfrac{2}{3}\) giờ. - Tính quãng đường ô tô đi được trong \(\dfrac{2}{3}\) giờ. - Tính quãng đường ô tô và xe máy cùng chuyển động ngược chiều ta lấy độ dài quãng đường AB trừ đi quãng đường ô tô đi được trong \(\dfrac{2}{3}\) giờ. - Tính tổng vận tốc hai xe. - Thời gian đi để gặp nhau \(=\) quãng đường \(:\) tổng vận tốc hai xe. - Khoảng cách từ chỗ gặp nhau đến B chính là quãng đường mà xe máy đã đi từ lúc xuất phát đến lúc gặp nhau. Để tính quãng đường đó ta lấy vận tốc xe máy nhân với thời gian đi để gặp nhau. Lời giải chi tiết :
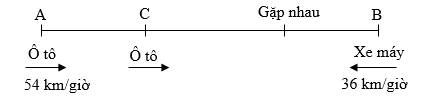
Ta có sơ đồ chuyển động của hai xe như sau:
Đổi: $40$ phút \( = \,\dfrac{2}{3}\) giờ Trong \(\dfrac{2}{3}\) giờ, ô tô đi được quãng đường AC dài là: \(54 \times \dfrac{2}{3} = 36 \;(km)\) Quãng đường BC dài là: \(81 - 36 = 45 \;(km)\) Tổng vận tốc của hai xe là: \(54 + 36 = 90\) (km/giờ) Thời gian đi để hai xe gặp nhau là: \(45:90 = 0,5\) (giờ) Chỗ gặp nhau cách B số ki-lô-mét là: \(36 \times 0,5 = 18 \;(km)\) Đáp số: \(0,5\) giờ; \(18km\). Chú ý
- Học sinh có thể không đọc kĩ đề bài để xác định rằng hai xe xuất phát không cùng lúc nên tính thời gian đi để gặp nhau bằng độ dài quãng đường AB chia cho tổng hai vận tốc. - Học sinh có thể sai khi xác định khoảng cách từ chỗ gặp nhau đến B là quãng đường mà ô tô đã đi từ lúc xuất phát đến lúc gặp nhau. - Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách lấy quãng đường BC chia cho hiệu vận tốc.
Câu 10 :
Điền số thích hợp vào ô trống: Lúc \(8\) giờ $30$ phút ô tô thứ nhất đi từ A đến B với vận tốc $44$ km/giờ. Lúc $9$ giờ ô tô thứ hai đi từ B để đến A với vận tốc $56$ km/giờ. Hai xe gặp nhau lúc $10$ giờ $45$ phút. Vậy độ dài quãng đường AB là \(km\). Đáp án
Lúc \(8\) giờ $30$ phút ô tô thứ nhất đi từ A đến B với vận tốc $44$ km/giờ. Lúc $9$ giờ ô tô thứ hai đi từ B để đến A với vận tốc $56$ km/giờ. Hai xe gặp nhau lúc $10$ giờ $45$ phút. Vậy độ dài quãng đường AB là \(km\). Phương pháp giải :
Theo đề bài, hai ô tô xuất phát không cùng lúc. Đến $9$ giờ thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau: - Tính thời gian ô tô thứ nhất đi trước ô tô thứ hai: $9$ giờ \( - 8\) giờ $30$ phút \( = 30\) phút và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ. - Tính quãng đường ô tô đi được trong \(30\) phút. - Tính thời gian đi để gặp nhau ta lấy thời gian lúc gặp nhau trừ đi thời gian lúc ô tô thứ hai xuất phát: $10$ giờ $45$ phút $ - \,9$ giờ và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ. - Tính tổng vận tốc hai xe. - Tính quãng đường ô tô và xe máy chuyển động ngược chiều ta lấy tổng vận tốc nhân với thời gian đi để gặp nhau. - Độ dài quãng đường AB bằng tổng quãng đường ô tô đi được trong \(30\) phút và quãng đường ô tô và xe máy chuyển động ngược chiều. Lời giải chi tiết :
Ta có sơ đồ chuyển động của hai xe như sau:
Thời gian ô tô thứ nhất đi trước ô tô thứ hai là: $9$ giờ \( - \,8\) giờ $30$ phút \( = \,30\) phút Đổi: $30$ phút \( = \,0,5\) giờ Trong \(0,5\) giờ, ô tô đi được quãng đường AC dài là: \(44 \times \,0,5 = 22 \;(km)\) Thời gian đi để hai xe gặp nhau (kể từ khi ô tô thứ hai xuất phát) là: $10$ giờ $45$ phút $ - \,9$ giờ $ = \,1$ giờ $45$ phút Đổi $1$ giờ $45$ phút \( = \,1,75\) giờ Tổng vận tốc của hai xe là: \(44 + 56 = 100\) (km/giờ) Quãng đường BC dài là: \(100 \times 1,75 = 175\;(km)\) Quãng đường AB dài là: \(22 + 175 = 197\;(km)\) Đáp số: \(197km\). Vậy đáp án đúng điền vào ô trống là \(197\). Chú ý
- Học sinh cần đọc kĩ đề bài và xác định được thời gian lúc hai xe cùng chuyển động. - Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách tính $10$ giờ $45$ phút $ - \,9$ giờ rồi nhân với hiệu vận tốc để tìm quãng đường BC, từ đó tìm độ dài quãng đường AB. - Học sinh có thể làm sai khi tính thời gian đi để gặp nhau bằng cách tính $10$ giờ $45$ phút $ - \,8$ giờ \(30\) phút rồi nhân với tổng vận tốc để tìm độ dài quãng đường AB.
Câu 11 :
Lúc \(7\) giờ, xe thứ nhất đi từ A đến B với vận tốc $40$ km/giờ. Đến \(7\) giờ \(45\) phút, xe thứ hai đi từ B đến A. Đến \(9\) giờ hai xe gặp nhau. Hỏi xe thứ hai đi với vận tốc bao nhiêu, biết rằng quãng đường AB dài $142,5km$. A. \(16,25\) km/giờ B. \(31,25\) km/giờ C. \(50\) km/giờ D. \(74\) km/giờ Đáp án
C. \(50\) km/giờ Phương pháp giải :
Theo đề bài, hai xe xuất phát không cùng lúc. Đến $7$ giờ \(45\) phút thì hai xe mới cùng chuyển động. Để giải bài này ta làm như sau: - Tính thời gian xe thứ nhất đi trước xe thứ hai: $7$ giờ $45$ phút \( - \,7\) giờ \( = \,45\) phút và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ. - Tính quãng đường xe thứ nhất đi được trong \(45\) phút. - Tính thời gian đi để gặp nhau ta lấy thời gian lúc gặp nhau trừ đi thời gian lúc xe thứ hai xuất phát: $9$ giờ $ - \,7$ giờ $45$ phút và đổi kết quả vừa tìm được sang dạng số thập phân có đơn vị là giờ. - Tính quãng đường hai xe chuyển động ngược chiều ta lấy độ dài quãng đường AB trừ đi quãng đường xe thứ nhất đi được trong \(45\) phút. - Tính tổng vận tốc hai xe ta lấy quãng đường ô tô và xe máy chuyển động ngược chiều chia cho thời gian đi để gặp nhau. - Tính vận tốc xe thứ hai ta lấy tổng vận tốc trừ đi vận tốc xe thứ nhất. Lời giải chi tiết :
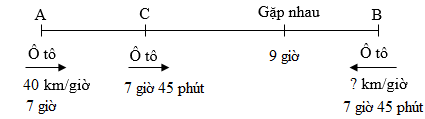
Ta có sơ đồ chuyển động của hai xe như sau:
Thời gian ô tô thứ nhất đi trước ô tô thứ hai là: $7$ giờ $45$ phút \( - \,7\) giờ \( = \,45\) phút Đổi: $45$ phút \( = \,0,75\) giờ Trong \(0,75\) giờ, ô tô đi được quãng đường AC dài là: \(40 \times \,0,75 = 30\;(km)\) Thời gian đi để hai xe gặp nhau (kể từ khi ô tô thứ hai xuất phát) là: $9$ giờ $ - \,7$ giờ $45$ phút $ = \,1$ giờ $15$ phút Đổi $1$ giờ $15$ phút \( = \,1,25\) giờ Quãng đường BC dài là: \(142,5 - 30 = 112,5\;(km)\) Tổng vận tốc của hai xe là: \(112,5:1,25 = 90\) (km/giờ) Vận tốc xe thứ hai là: \(90 - 40 = 50\) (km/giờ) Đáp số: \(50\) km/giờ. Chú ý
- Học sinh cần đọc kĩ đề bài và xác định được thời gian lúc hai xe cùng chuyển động. - Học sinh có thể làm sai khi tính tổng vận tốc bằng cách lấy độ dài quãng đường AB chia cho thời gian đi để gặp nhau là \(9\) giờ \( - \,\,7\) giờ, từ đó tìm vận tốc xe thứ hai là \(31,25\) km/giờ; hoặc tính tổng vận tốc bằng cách lấy độ dài quãng đường AB chia cho thời gian đi để gặp nhau là \(9\) giờ \( - \,\,7\) giờ \(45\) phút, từ đó tìm vận tốc xe thứ hai là \(74\) km/giờ. - Học sinh có thể làm sai khi tính tổng vận tốc bằng cách lấy độ dài quãng đường BC chia cho thời gian đi để gặp nhau là \(9\) giờ \( - \,\,7\) giờ, từ đó tìm vận tốc xe thứ hai là \(16,25\) km/giờ.
|


















.png)







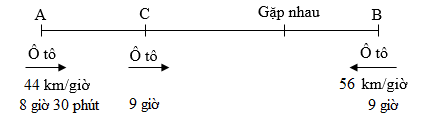





Danh sách bình luận