Trắc nghiệm: Bảng đơn vị đo thời gian Toán 5Đề bài
Câu 1 :
Điền số thích hợp vào ô trống: \(1\) giờ = phút.
Câu 2 :
Điền số thích hợp vào ô trống: Tháng hai (năm nhuận) có ngày.
Câu 3 :
Điền số thích hợp vào ô trống: \(3\) giờ = phút.
Câu 4 :
Điền số thích hợp vào ô trống: \(2,5\) phút = giây.
Câu 5 :
\(\dfrac{5}{4}\) ngày \(= \,….\) giờ. Số thích hợp điền vào chỗ chấm là: A. \(54\) giờ B. \(50\) giờ C. \(30\) giờ D. \(25\) giờ
Câu 6 :
Bạn An nói “\(1,6\) giờ \( = 1\) giờ \(6\) phút”. Vậy An nói đúng hay sai? A. Đúng B. Sai
Câu 7 :
Bạn Hà nói “\(2\) năm \( = 24\) tháng”. Vậy Hà nói đúng hay sai? A. Đúng B. Sai
Câu 8 :
Một chiếc máy khâu được phát minh năm $1898$. Hỏi chiếc máy khâu đó được phát minh vào thế kỉ nào? A. Thế kỉ \(XVIII\) B. Thế kỉ \(XIX\) C. Thế kỉ \(XX\) D. Thế kỉ $XXI$
Câu 9 :
Điền số thích hợp vào ô trống: \(155\) phút = giờ phút.
Câu 10 :
\(5\) năm \(6\) tháng = …. năm. Số thích hợp điền vào chỗ chấm là: A. \(66\) B. \(56\) C. \(5,6\) D. \(5,5\)
Câu 11 :
Viết số thập phân thích hợp vào ô trống : \(204\) giây = phút.
Câu 12 :
Điền dấu thích hợp vào ô trống: \(3,5\) năm \(35\) tháng
Câu 13 :
Điền số thích hợp vào ô trống: An đi từ nhà đến trường hết \(0,45\) giờ. Vậy An đi từ nhà đến trường hết phút.
Câu 14 :
Quãng đường AB dài $306 m$, một vận động viên chạy hết \(4\) phút \(15\) giây. Hỏi mỗi phút vận động viên đó chạy được bao nhiêu mét ? A. \(74m\) B. \(72m\) C. \(70m\) D. \(68m\)
Câu 15 :
Một ô tô được phát minh năm \(1886\). Một chiếc máy bay được phát minh sau ô tô đó là \(17\) năm. Hỏi chiếc máy bay đó được phát minh vào thế kỉ nào? A. Thế kỉ \(XVIII\) B. Thế kỉ \(XIX\) C. Thế kỉ \(XX\) D. Thế kỉ $XXI$
Câu 16 :
Quãng đường AB dài $3000m$, vận động viên A chạy hết \(12,6\) phút, vận động viên B chạy hết $754$ giây, vận động viên C chạy hết $0,2$ giờ. Hỏi ai chạy nhanh nhất? A. Vận động viên A B. Vận động viên B C. Vận động viên C
Câu 17 :
Ngày \(28\) tháng \(3\) năm \(2017\) là thứ ba. Hỏi ngày \(28\) tháng \(3\) năm \(2019\) là thứ mấy? A. Thứ ba B. Thứ năm C. Thứ bảy D. Chủ nhật Lời giải và đáp án
Câu 1 :
Điền số thích hợp vào ô trống: \(1\) giờ = phút. Đáp án
\(1\) giờ = phút. Lời giải chi tiết :
Ta có: \(1\) giờ = \(60\) phút Vậy đáp án đúng điền vào ô trống là \(60\).
Câu 2 :
Điền số thích hợp vào ô trống: Tháng hai (năm nhuận) có ngày. Đáp án
Tháng hai (năm nhuận) có ngày. Lời giải chi tiết :
Tháng hai có \(28\) ngày, tháng hai năm nhuận có \(29\) ngày. Vậy đáp án đúng điền vào ô trống là \(29\).
Câu 3 :
Điền số thích hợp vào ô trống: \(3\) giờ = phút. Đáp án
\(3\) giờ = phút. Phương pháp giải :
\(1\) giờ = $60$ phút . Muốn đổi một số từ đơn vị giờ sang phút ta lấy 60 phút nhân với số đó. Lời giải chi tiết :
Ta có \(1\) giờ $=60$ phút nên \(3\) giờ $ = 60$ phút \( \times \,3\, = \,180\) phút. Vậy số thích hợp điền vào ô trống là \(180\).
Câu 4 :
Điền số thích hợp vào ô trống: \(2,5\) phút = giây. Đáp án
\(2,5\) phút = giây. Phương pháp giải :
\(1\) phút $= 60$ giây. Muốn đổi một số từ đơn vị phút sang giây ta lấy 60 giây nhân với số đó. Lời giải chi tiết :
Ta có \(1\) phút = $60$ giây nên \(2,5\) phút $ = 60$ giây \( \times \,\,2,5\,\, = \,\,150\) giây Vậy đáp án cần điền vào ô trống là \(150\).
Câu 5 :
\(\dfrac{5}{4}\) ngày \(= \,….\) giờ. Số thích hợp điền vào chỗ chấm là: A. \(54\) giờ B. \(50\) giờ C. \(30\) giờ D. \(25\) giờ Đáp án
C. \(30\) giờ Phương pháp giải :
\(1\) ngày $=\,24$ giờ . Muốn đổi một số từ đơn vị ngày sang giờ ta lấy \(24\) giờ nhân với số đó. Lời giải chi tiết :
Ta có \(1\) ngày $=\, 24$ giờ. Do đó, \(\dfrac{5}{4}\) ngày $ = 24$ giờ \( \times \,\dfrac{5}{4}\,=\,30\) giờ. Vậy \(\dfrac{5}{4}\) ngày \(=\,30\) giờ. Chú ý
Học sinh có thể làm sai khi xác định \(1\) ngày = $20$ giờ.
Câu 6 :
Bạn An nói “\(1,6\) giờ \( = 1\) giờ \(6\) phút”. Vậy An nói đúng hay sai? A. Đúng B. Sai Đáp án
A. Đúng B. Sai Phương pháp giải :
\(1\) giờ = $60$ phút. Muốn đổi một số từ đơn vị giờ sang phút ta lấy \(60\) phút nhân với số đó. Lời giải chi tiết :
Ta có \(1\) giờ = $60$ phút nên \(1,6\) giờ $ = 60$ phút $ \times \,\,1,6\,\, = \,\,96$ phút \( = 1\) giờ \(36\) phút Vậy bạn An đã nói sai.
Câu 7 :
Bạn Hà nói “\(2\) năm \( = 24\) tháng”. Vậy Hà nói đúng hay sai? A. Đúng B. Sai Đáp án
A. Đúng B. Sai Phương pháp giải :
\(1\) năm \( = \,\,12\) tháng. Muốn đổi một số từ đơn vị năm sang tháng ta lấy \(12\) tháng nhân với số đó. Lời giải chi tiết :
Ta có \(1\) năm \( = \,\,12\) tháng nên \(2\) năm \( = \,\,12\) tháng \( \times \,\,2\, = \,24\) tháng. Vậy bạn Hà nói đúng.
Câu 8 :
Một chiếc máy khâu được phát minh năm $1898$. Hỏi chiếc máy khâu đó được phát minh vào thế kỉ nào? A. Thế kỉ \(XVIII\) B. Thế kỉ \(XIX\) C. Thế kỉ \(XX\) D. Thế kỉ $XXI$ Đáp án
B. Thế kỉ \(XIX\) Phương pháp giải :
Từ năm \(1\) đến năm $100$ là thế kỉ một ( thế kỉ $I$) Từ năm $101$ đến năm \(200\) là thế kỉ hai ( thế kỉ $II$) ... Từ năm $1801$ đến năm $1900$ là thế kỉ mười chín ( thế kỉ $XIX$) Từ năm $1901$ đến năm $2000$ là thế kỉ hai mươi ( thế kỉ $XX$) Từ năm $2001$ đến năm $2100$ là thế kỉ hai mươi mốt ( thế kỉ $XXI$) Lời giải chi tiết :
Ta có: Từ năm $1801$ đến năm $1900$ là thế kỉ mười chín ( thế kỉ $XIX$). Do đó, chiếc máy khâu phát minh năm $1898$ thuộc thế kỉ $XIX$.
Câu 9 :
Điền số thích hợp vào ô trống: \(155\) phút = giờ phút. Đáp án
\(155\) phút = giờ phút. Phương pháp giải :
\(1\) giờ $ = 60$ phút nên ta thực hiện tính phép chia \(155:60\). Thương chính là số giờ còn số dư là số phút. Lời giải chi tiết :
Ta có: Vậy \(155\) phút = \(2\) giờ \(35\) phút Đáp án đúng điền vào ô trống theo thứ tự từ trái sang phải là \(2\,;\,\,35\).
Câu 10 :
\(5\) năm \(6\) tháng = …. năm. Số thích hợp điền vào chỗ chấm là: A. \(66\) B. \(56\) C. \(5,6\) D. \(5,5\) Đáp án
D. \(5,5\) Phương pháp giải :
- Đổi \(5\) năm \(6\) tháng \( = \,5\) năm \( + \,\,6\) tháng \( = 12\) tháng \( \times \,5\) \( + \,\,6\) tháng \( = \,\,66\) tháng - Khi đổi một số có đơn vị là tháng sang năm ta chỉ cần lấy số đó chia cho $12$. Lời giải chi tiết :
Ta có: \(5\) năm \(6\) tháng \( = \,5\) năm \( + \,\,6\) tháng \( = 12\) tháng \( \times \,5\) \( + \,\,6\) tháng \( = \,\,66\) tháng. Vậy \(66\) tháng \( = 5,5\) năm hay \(5\) năm \(6\) tháng \( = \,5,5\) năm. Chú ý
- Học sinh có thể không đọc kĩ bài nên đổi \(5\) năm \(6\) tháng theo đơn vị là tháng, xác định \(1\) năm \( = 12\) tháng hoặc xác định sai \(1\) năm \( = 10\) tháng, do đó có thể chọn đáp án sai là A hoặc B. - Có thể xác định sai \(1\) năm \( = 10\) tháng nên tính \(5\) năm \(6\) tháng \( = \,5,6\) năm.
Câu 11 :
Viết số thập phân thích hợp vào ô trống : \(204\) giây = phút. Đáp án
\(204\) giây = phút. Phương pháp giải :
\(1\) phút $ = 60$ giây. Khi đổi một số có đơn vị là giây sang phút ta chỉ cần lấy số đó chia cho $60$. Lời giải chi tiết :
Ta có: \(204\) giây \(=\, 3,4\) phút. Vậy số thập phân thích hợp điền vào ô trống là \(3,4\).
Câu 12 :
Điền dấu thích hợp vào ô trống: \(3,5\) năm \(35\) tháng Đáp án
\(3,5\) năm \(35\) tháng Phương pháp giải :
- Đưa về cùng đơn vị đo thời gian là tháng để so sánh. - \(1\) năm $ = \,12$ tháng. Để đổi một số có đơn vị đo là năm sang đơn vị đo là tháng ta chỉ việc lấy \(12\) tháng nhân với số đó. Lời giải chi tiết :
Ta có: \(1\) năm \( = 12\) tháng. Do đó: \(3,5\) năm \( = 12\) tháng \( \times \,3,5\, = \,42\) tháng. Mà \(42\) tháng $ > \,35$ tháng nên \(3,5\) năm \( > \,35\) tháng. Chú ý
Học sinh có thể xác định sai \(1\) năm \( = 10\) tháng, từ đo tính được \(3,5\) năm \( = 35\) tháng, do đó chọn đáp án sai là dấu \( = \) .
Câu 13 :
Điền số thích hợp vào ô trống: An đi từ nhà đến trường hết \(0,45\) giờ. Vậy An đi từ nhà đến trường hết phút. Đáp án
An đi từ nhà đến trường hết \(0,45\) giờ. Vậy An đi từ nhà đến trường hết phút. Phương pháp giải :
\(1\) giờ \( = 60\) phút. Tính thời gian An đi từ nhà đến trường hết bao nhiêu phút ta chỉ cần lấy \(60\) phút nhân với \(0,45\). Lời giải chi tiết :
An đi từ nhà đến trường hết số phút là: \(60 \times 0,45 = 27\) (phút) Đáp số: \(27\) phút. Vậy đáp án đúng điền vào ô trống là \(27\).
Câu 14 :
Quãng đường AB dài $306 m$, một vận động viên chạy hết \(4\) phút \(15\) giây. Hỏi mỗi phút vận động viên đó chạy được bao nhiêu mét ? A. \(74m\) B. \(72m\) C. \(70m\) D. \(68m\) Đáp án
B. \(72m\) Phương pháp giải :
- Đổi thời gian vận động viên đó chạy về đơn vị là phút. \(4\) phút \(15\) giây \( = 4\) phút \( + \,15\) giây \( = 4\) phút \( + \,(\,15:60)\) phút \( = 4\) phút \( + \,0,25\) phút \( = 4,25\) phút. - Tính quãng đường vận động viên chạy được trong mỗi phút ta lấy quãng đường vận động viên đã chạy chia cho thời gian vận động viên đã chạy. Lời giải chi tiết :
Đổi \(4\) phút \(15\) giây \( = 4,25\) phút Mỗi phút vận động viên chạy được số mét là: \(306:4,25 = 72 \;(m)\) Đáp số: \(72m\).
Câu 15 :
Một ô tô được phát minh năm \(1886\). Một chiếc máy bay được phát minh sau ô tô đó là \(17\) năm. Hỏi chiếc máy bay đó được phát minh vào thế kỉ nào? A. Thế kỉ \(XVIII\) B. Thế kỉ \(XIX\) C. Thế kỉ \(XX\) D. Thế kỉ $XXI$ Đáp án
C. Thế kỉ \(XX\) Phương pháp giải :
Từ năm \(1\) đến năm $100$ là thế kỉ một ( thế kỉ $I$ ) Từ năm $101$ đến năm 200 là thế kỉ hai ( thế kỉ $II$) ... Từ năm $1801$ đến năm $1900$ là thế kỉ mười chín ( thế kỉ $XIX$) Từ năm $1901$ đến năm $2000$ là thế kỉ hai mươi ( thế kỉ $XX$) Từ năm $2001$ đến năm $2100$ là thế kỉ hai mươi mốt ( thế kỉ $XXI$) - Chiếc máy bay được phát minh sau ô tô đó là \(17\) năm nên tính thời gian phát minh máy bay ta lấy năm phát minh ô tô cộng thêm \(17\) năm. Sau đó dựa vào bảng trên để xác định thế kỉ. Lời giải chi tiết :
Máy bay được phát minh vào năm: \(1886 + 17 = 1903\) Từ năm $1901$ đến năm $2000$ là thế kỉ hai mươi ( thế kỉ $XX$) nên năm \(1903\) thuộc thế kỉ hai mươi. Do đó, chiếc máy bay đó được phát minh vào thế kỉ hai mươi (thế kỉ $XX$). Chú ý
Học sinh có thể làm sai khi tính thời gian phát minh máy bay bằng cách lấy năm phát minh ô tô trừ đi \(17\) năm, từ đó xác định thế kỉ phát minh ra máy bay là thế kỉ \(XIX\)
Câu 16 :
Quãng đường AB dài $3000m$, vận động viên A chạy hết \(12,6\) phút, vận động viên B chạy hết $754$ giây, vận động viên C chạy hết $0,2$ giờ. Hỏi ai chạy nhanh nhất? A. Vận động viên A B. Vận động viên B C. Vận động viên C Đáp án
C. Vận động viên C Phương pháp giải :
- Đổi các đơn vị thời gian về cùng một đơn vị (có thể đổi về cùng đơn vị là giờ, phút hoặc giây…) - So sánh thời gian các vận động viên đã chạy, thời gian của ai ít nhất thì người đó chạy nhanh nhất. Lời giải chi tiết :
Ta có: \(12,6\) phút $ = 60$ giây \( \times \,\,12,6\,\, = \,\,756\) giây; \(0,2\) giờ $ = 60$ phút \( \times \,\,0,2\,\, = \,12\,\,\) phút $ = 60$ giây \( \times \,\,12\,\, = \,720\) giây; Ta thấy: \(720\) giây $ < {\rm{ 754}}$ giây $ < {\rm{ 756}}$ giây. Hay $0,2$ giờ \( < \,\,\,754\) giây \( < \,\,12,6\) phút. Vậy vận động viên C chạy nhanh nhất. Chú ý
- Ta có thể đưa về cùng đơn vị là giờ hoặc phút. - Chú ý tính toán cẩn thận.
Câu 17 :
Ngày \(28\) tháng \(3\) năm \(2017\) là thứ ba. Hỏi ngày \(28\) tháng \(3\) năm \(2019\) là thứ mấy? A. Thứ ba B. Thứ năm C. Thứ bảy D. Chủ nhật Đáp án
B. Thứ năm Phương pháp giải :
- Tính số ngày từ ngày \(28\) tháng \(3\) năm \(2017\) đến ngày \(28\) tháng \(3\) năm \(2019\). - Lấy số ngày đó chia cho \(7\) để xác định số tuần và số ngày dư. Sau đó dựa vào đó để lập luận tìm ngày \(28\) tháng \(3\) năm \(2019\) là thứ mấy. Lời giải chi tiết :
Từ ngày \(28\) tháng \(3\) năm \(2017\) đến ngày \(28\) tháng \(3\) năm \(2019\) có số ngày là: \(365 \times 2 = 730\) (ngày) Ta có: \(730:7 = 104\) dư \(2\) Vì ngày \(28\) tháng \(3\) năm \(2017\) là thứ ba nên ngày \(28\) tháng \(3\) năm \(2019\) là thứ năm.
|































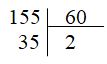
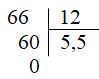
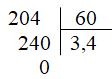





Danh sách bình luận