Trắc nghiệm: Viết các số đo diện tích dưới dạng số thập phân Toán 5Đề bài
Câu 1 :
Chọn số thích hợp để điền vào chỗ chấm: $2{m^2}\;5d{m^2} \;= \;...\;d{m^2}$ A. \(25\) B. \(205\) C. \(250\) D. \(2005\)
Câu 2 :
Điền số thích hợp vào ô trống: \(5ha\,42{m^2} = \) ${m^2}$
Câu 3 :
Chọn số thích hợp để điền vào chỗ chấm : $37d{m^2}\;21c{m^2} = ...d{m^2}$ A. \(3,721\) B. \(37,0021\) C. \(37,21\) D. \(372,1\)
Câu 4 :
Điền số thích hợp vào ô trống: \(13k{m^2}\;8ha = \) $k{m^2}$
Câu 5 :
Điền số thích hợp vào ô trống: \(361d{m^2} = \) $da{m^2}$
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm : $48267m{m^2} = \;...d{m^2}$ A. \(4,8267\) B. \(48,267\) C. \(482,67\) D. \(4826,7\)
Câu 7 :
Điền số thích hợp vào ô trống: \(5,7ha = \) \({m^2}\).
Câu 8 :
$34d{m^2}\,5c{m^2}\,...\,$ $34,5d{m^2}$ Dấu thích hợp điền vào chỗ chấm là: A. \( > \) B. \( < \) C. \( = \)
Câu 9 :
Một hình vuông có độ dài cạnh là \(28cm\). Tính diện tích hình vuông đó. A. \(7c{m^2}\) B. \(7,84d{m^2}\) C. \(49d{m^2}\) D. \(112c{m^2}\)
Câu 10 :
Điền số thích hợp vào ô trống: Một sân trường hình chữ nhật có chu vi là \(168m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Vậy diện tích sân trường đó là \(km^2\). Lời giải và đáp án
Câu 1 :
Chọn số thích hợp để điền vào chỗ chấm: $2{m^2}\;5d{m^2} \;= \;...\;d{m^2}$ A. \(25\) B. \(205\) C. \(250\) D. \(2005\) Đáp án
B. \(205\) Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho: \({m^2}\) và \(d{m^2}\). - Tìm mối liên hệ giữa chúng: $1{m^2} = 100d{m^2}$. - Đổi \(2m^2\) sang đơn vị đo \(dm^2\) rồi cộng thêm với \(5dm^2\). Lời giải chi tiết :
Theo bảng đơn vị đo diện tích ta có $1{m^2} = 100d{m^2}$ nên $2{m^2} = 200d{m^2}$. Do đó $2{m^2}\;5d{m^2} = 2{m^2} + 5d{m^2} = 200d{m^2} + 5d{m^2} $ $= 205d{m^2}$ Vậy $2{m^2}\;5d{m^2} = 205d{m^2}$.
Câu 2 :
Điền số thích hợp vào ô trống: \(5ha\,42{m^2} = \) ${m^2}$ Đáp án
\(5ha\,42{m^2} = \) ${m^2}$ Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho: \({m^2}\) và \(ha\). - Tìm mối liên hệ giữa chúng: $1ha = 10000{m^2}$. - Đổi \(5ha\) sang đơn vị đo là \(m^2\), sau đó cộng thêm với \(42m^2\). Lời giải chi tiết :
Theo bảng đơn vị đo diện tích ta có $1ha = 10000{m^2}$ nên $5ha = 50000{m^2}$. Do đó $5ha\,42{m^2} = 5\, ha + 42 {m^2} $ $= 50000{m^2} + 42{m^2} $ $= 50042{m^2}$ Vậy đáp án đúng điền vào ô trống là \(50042\).
Câu 3 :
Chọn số thích hợp để điền vào chỗ chấm : $37d{m^2}\;21c{m^2} = ...d{m^2}$ A. \(3,721\) B. \(37,0021\) C. \(37,21\) D. \(372,1\) Đáp án
C. \(37,21\) Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho (\(d{m^2}\) và \(c{m^2}\)) và tìm mối liên hệ giữa chúng: \(1d{m^2} = 100c{m^2}\) hay \(1c{m^2} = \dfrac{1}{{100}}d{m^2}\). - Đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân gọn nhất. Lời giải chi tiết :
Theo bảng đơn vị đo diện tích ta có \(1d{m^2} = 100c{m^2}\) hay \(1c{m^2} = \dfrac{1}{{100}}d{m^2}\). Nên $37d{m^2}\;21c{m^2} = 37\,\dfrac{{21}}{{100}}d{m^2}= 37,21d{m^2}$. Vậy $37d{m^2}\;21c{m^2} = 37,21d{m^2}$.
Câu 4 :
Điền số thích hợp vào ô trống: \(13k{m^2}\;8ha = \) $k{m^2}$ Đáp án
\(13k{m^2}\;8ha = \) $k{m^2}$ Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho là (\(k{m^2}\), \(ha\)) và tìm mối liên hệ giữa chúng: \(1k{m^2} = 100ha\) hay \(1ha = \dfrac{1}{{100}}k{m^2}\). - Đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân - Đổi hỗn số vừa tìm được thành số thập phân gọn nhất. Lời giải chi tiết :
Theo bảng đơn vị đo diện tích ta có \(1k{m^2} = 100\,ha\) hay \(1ha = \dfrac{1}{{100}}k{m^2}\). Nên $13k{m^2}\;8\,ha = 13\,\dfrac{8}{{100}}k{m^2} = 13,08k{m^2}$ Vậy đáp án đúng điền vào ô trống là \(13,08\).
Câu 5 :
Điền số thích hợp vào ô trống: \(361d{m^2} = \) $da{m^2}$ Đáp án
\(361d{m^2} = \) $da{m^2}$ Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho (\(da{m^2}\) và \(d{m^2}\)) và tìm mối liên hệ giữa chúng: \(1da{m^2} = 10000d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{10000}}da{m^2}\). - Đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân gọn nhất. Lời giải chi tiết :
Theo bảng đơn vị đo diện tích ta có \(1da{m^2} = 10000d{m^2}\) hay \(1d{m^2} = \dfrac{1}{{10000}}da{m^2}\). Nên $361d{m^2}\, = \dfrac{{361}}{{10000}}da{m^2} $$= 0,0361da{m^2}$ Vậy đáp án đúng điền vào ô trống là \(0,0361\).
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm : $48267m{m^2} = \;...d{m^2}$ A. \(4,8267\) B. \(48,267\) C. \(482,67\) D. \(4826,7\) Đáp án
A. \(4,8267\) Phương pháp giải :
- Xác định hai đơn vị đo diện tích đã cho (\(d{m^2}\) và \(m{m^2}\)) và tìm mối liên hệ giữa chúng: \(1d{m^2} = 10000m{m^2}\) hay \(1m{m^2} = \dfrac{1}{{10000}}d{m^2}\). - Đổi $48267m{m^2} = 40000m{m^2} + 8267m{m^2}$, rồi đổi số đo diện tích đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân. Lời giải chi tiết :
Ta có: \(\begin{array}{l}48267m{m^2} \\= 40000m{m^2} + 8267m{m^2} \\= 4d{m^2} + 8267m{m^2}\\ = 4\dfrac{{8267}}{{10000}}d{m^2} \\= 4,8267d{m^2}\end{array}\) Vậy $48267m{m^2} = 4,8267d{m^2}$.
Câu 7 :
Điền số thích hợp vào ô trống: \(5,7ha = \) \({m^2}\). Đáp án
\(5,7ha = \) \({m^2}\). Phương pháp giải :
- Xác định các đơn vị đo diện tích đã cho là \({m^2};\,ha\) và tìm mối liên hệ giữa chúng: \(1ha = 10000{m^2}\) hay \(1{m^2} = \dfrac{1}{{10000}}ha\). - Viết \(5,7ha\) dưới dạng hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số trên thành số đo diện tích có đơn vị là \({m^2}\). Lời giải chi tiết :
Ta có: \(5,7ha = 5\dfrac{7}{{10}}ha = 5\dfrac{{7000}}{{10000}}ha= 5ha + \dfrac{{7000}}{{10000}}ha \) \(= 50000{m^2} + 7000{m^2}= 57000{m^2}\) Vậy \(5,7ha=57000m^2\). Đáp án cần điền vào ô trống là \(57000\).
Câu 8 :
$34d{m^2}\,5c{m^2}\,...\,$ $34,5d{m^2}$ Dấu thích hợp điền vào chỗ chấm là: A. \( > \) B. \( < \) C. \( = \) Đáp án
B. \( < \) Phương pháp giải :
- Đưa hai số đo về cùng một dạng là dạng số thập phân. - Xác định các số đo đã cùng đơn vị đo chưa, nếu không cùng đơn vị đo ta phải đổi thành cùng 1 đơn vị đo. - Xác định các phần nguyên và phần thập phân để so sánh bình thường như so sánh các số thập phân. Lời giải chi tiết :
Hai số đã cho chưa cùng đơn vị đo, ta sẽ đưa về cùng dạng số thập phân có đơn vị đo là \(d{m^2}\). Ta có: $34d{m^2}\;5c{m^2} = 34\,\dfrac{5}{{100}}d{m^2}= 34,05d{m^2}$. So sánh hai số $34,05d{m^2}$ và $34,5d{m^2}$ ta thấy $34,05 < 34,5$ nên $34,05d{m^2} < 34,5d{m^2}$. Hay $34d{m^2}\,5c{m^2} < 34,5d{m^2}$. Vậy đáp án đúng là dấu \( < \).
Câu 9 :
Một hình vuông có độ dài cạnh là \(28cm\). Tính diện tích hình vuông đó. A. \(7c{m^2}\) B. \(7,84d{m^2}\) C. \(49d{m^2}\) D. \(112c{m^2}\) Đáp án
B. \(7,84d{m^2}\) Phương pháp giải :
- Tính diện tích hình vuông ta lấy cạnh nhân với cạnh. Lời giải chi tiết :
Diện tích hình vuông đó là: \(28 \times 28 = 784(c{m^2})\) \(784c{m^2} = 7,84d{m^2}\) Đáp số: \(7,84d{m^2}\).
Câu 10 :
Điền số thích hợp vào ô trống: Một sân trường hình chữ nhật có chu vi là \(168m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Vậy diện tích sân trường đó là \(km^2\). Đáp án
Một sân trường hình chữ nhật có chu vi là \(168m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Vậy diện tích sân trường đó là \(km^2\). Phương pháp giải :
- Hình chữ nhật có chu vi bằng \(168m\) chiều rộng bằng \(\dfrac{3}{4}\) chiều dài. Tìm nửa chu vi hình chữ nhật, khi đó ta có bài toán tìm hai số khi biết tổng và tỉ số. Giải bài toán ta tìm được chiều rộng hình chữ nhật, chiều dài hình chữ nhật. - Tìm diện tích ta lấy chiều dài nhân với chiều rộng. - Đổi diện tích ra đơn vị \(k{m^2}\). Lời giải chi tiết :
Nửa chu vi sân trườnghình chữ nhật là: \(168:2 = 84(m)\) Ta có sơ đồ: 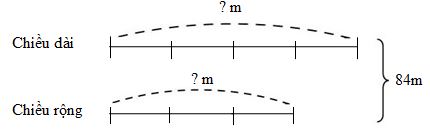 Theo sơ đồ, tổng số phần bằng nhau là: \(4 + 3 = 7\) (phần) Giá trị một phần là: \(84:7 = 12\;(m)\) Chiều dài sân trường là: \(12 \times 4 = 48\;(m)\) Chiều rộng sân trường là: \(12 \times 3 = 36\;(m)\) Diện tích sân trường là: \(48 \times 36 = 1728\;({m^2})\) Đổi \(1728{m^2} \)\(= \dfrac{{1728}}{{1000000}}k{m^2} \)\(= 0,001728k{m^2}\) Đáp số: \( 0,001728k{m^2}\). Vậy đáp án cần điền vào ô trống là \(0,001728.\)
|
