Trắc nghiệm: Ôn tập khái niệm về phân số. Tính chất cơ bản của phân số Toán 5Đề bài
Câu 1 :
Trong các cách viết phân số sau, cách viết nào sai?
Câu 2 :
Tử số của phân số \(\dfrac{{25}}{{37}}\) là
Câu 3 :
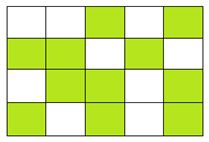
Phân số chỉ số ô vuông đã tô màu trong hình sau là:
Câu 4 :
Thương của phép chia \(9:14\) được viết dưới dạng phân số là:
Câu 5 :
Điền số thích hợp vào chỗ chấm: \(1 = \dfrac{{...}}{{99}}\)
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{2}{3} = \dfrac{8}{{...}}\)
Câu 7 :
\(\dfrac{8}{{14}}\) \(\dfrac{{16}}{{18}}\) \(\dfrac{{20}}{{35}}\) \(\dfrac{{52}}{{91}}\) \(\dfrac{{100}}{{185}}\)
Câu 8 :
Rút gọn phân số \(\dfrac{{15}}{{36}}\) thành phân số tối giản ta được phân số nào sau đây?
Câu 9 :
Câu 10 :
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản, sau đó quy đồng mẫu số ta được hai phân số lần lượt là:
Lời giải và đáp án
Câu 1 :
Trong các cách viết phân số sau, cách viết nào sai?
Đáp án : D Lời giải chi tiết :
\(\dfrac{3}{5};\,\,\dfrac{{18}}{1};\,\,\dfrac{0}{7}\) là các phân số vì có mẫu số khác \(0\). \(\dfrac{5}{0}\) không là phân số vì có số dưới gạch ngang bằng \(0\).
Câu 2 :
Tử số của phân số \(\dfrac{{25}}{{37}}\) là
Đáp án : A Lời giải chi tiết :
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang. Vậy tử số của phân số \(\dfrac{{25}}{{37}}\) là \(25\).
Câu 3 :
Phân số chỉ số ô vuông đã tô màu trong hình sau là:
Đáp án : B Phương pháp giải :
Quan sát hình vẽ, tìm ô vuông được tô màu và tổng số ô vuông, từ đó tìm được phân số. Lời giải chi tiết :
Quan sát hình vẽ ta thấy có tất cả \(20\) ô vuông, trong đó có \(11\) ô vuông được tô màu. Vậy phân số chỉ số ô vuông đã tô màu trong hình là \(\dfrac{{11}}{{20}}\).
Câu 4 :
Thương của phép chia \(9:14\) được viết dưới dạng phân số là:
Đáp án : C Phương pháp giải :
Dựa vào chú ý : Thương của phép chia số tự nhiên cho một số tự nhiên (khác \(0\)) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia. Lời giải chi tiết :
Ta có \(9:14 = \dfrac{9}{{14}}\). Vậy thương của phép chia \(9:14\) được viết dưới dạng phân số là \(\dfrac{9}{{14}}\).
Câu 5 :
Điền số thích hợp vào chỗ chấm: \(1 = \dfrac{{...}}{{99}}\)
Đáp án : D Phương pháp giải :
Số \(1\) có thể viết thành phân số có tử số và mẫu số bằng nhau và khác \(0\) . Lời giải chi tiết :
Ta có: \(1 = \dfrac{{99}}{{99}}\). Vậy số thích hợp điền vào ô trống là \(99\).
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{2}{3} = \dfrac{8}{{...}}\)
Đáp án : B Lời giải chi tiết :
Ta có : $8:2 = 4$. Nhân cả tử số và mẫu số của phân số \(\dfrac{2}{3}\)với \(4\) ta được \(\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\) Vậy số thích hợp điền vào chỗ chấm là \(12\).
Câu 7 :
\(\dfrac{8}{{14}}\) \(\dfrac{{16}}{{18}}\) \(\dfrac{{20}}{{35}}\) \(\dfrac{{52}}{{91}}\) \(\dfrac{{100}}{{185}}\) Đáp án
\(\dfrac{8}{{14}}\) \(\dfrac{{20}}{{35}}\) \(\dfrac{{52}}{{91}}\) Phương pháp giải :
Rút gọn các phân số rồi xác định các phân số bằng \(\frac{4}{7}\) Lời giải chi tiết :
Ta rút gọn các phân số, được: $\frac{8}{{14}} = \frac{{8:2}}{{14:2}} = \frac{4}{7}$ $\frac{{16}}{{18}} = \frac{{16:2}}{{18:2}} = \frac{8}{9}$ $\frac{{20}}{{35}} = \frac{{20:5}}{{35:5}} = \frac{4}{7}$ $\frac{{52}}{{91}} = \frac{{52:13}}{{91:13}} = \frac{4}{7}$ $\frac{{100}}{{185}} = \frac{{100:5}}{{185:5}} = \frac{{20}}{{37}}$ Vậy trong các phân số đã cho, phân số bằng với phân số \(\dfrac{4}{7}\) là \(\dfrac{8}{14};\,\dfrac{{20}}{{35}}; \, \dfrac{{52}}{{91}}\).
Câu 8 :
Rút gọn phân số \(\dfrac{{15}}{{36}}\) thành phân số tối giản ta được phân số nào sau đây?
Đáp án : B Phương pháp giải :
Bước 1: Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào (khác \(1\)) không? Bước 2: Chia cả tử số và mẫu số của phân số đó cho số tự nhiên vừa tìm được. Bước 3: Cứ làm như thế cho đến khi tìm được phân số tối giản. Lời giải chi tiết :
Ta có: \(\dfrac{{15}}{{36}} = \dfrac{{15:3}}{{36:3}} = \dfrac{5}{{12}}\). Vậy rút gọn phân số \(\dfrac{{15}}{{36}}\) ta được phân số tối giản là \(\dfrac{5}{{12}}\).
Câu 9 :
Đáp án : C Lời giải chi tiết :
Ta có : $637:49 = 13$. Chia cả tử số và mẫu số của phân số \(\dfrac{{637}}{{741}}\)cho \(13\) ta được \(\dfrac{{637}}{{741}} = \dfrac{{637:13}}{{741:13}} = \dfrac{{49}}{{57}}\) Vậy số thích hợp điền vào chỗ chấm là \(57\).
Câu 10 :
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản, sau đó quy đồng mẫu số ta được hai phân số lần lượt là:
Đáp án : D Phương pháp giải :
Bước 1: Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào (khác 1) không? Bước 2: Chia cả tử số và mẫu số của phân số đó cho số tự nhiên vừa tìm được. Bước 3: Cứ làm như thế cho đến khi tìm được phân số tối giản. Bước 4: Sau khi tìm được phân số tối giản ta sẽ quy đồng mẫu số hai phân số đó. Lời giải chi tiết :
Ta có: \(\begin{array}{l}\dfrac{{91}}{{117}} = \dfrac{{91:13}}{{117:13}} = \dfrac{7}{9};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{182}}{{224}} = \dfrac{{182:14}}{{224:14}} = \dfrac{{13}}{{16}}\\MSC = 9 \times 16 = 144\\\dfrac{7}{9} = \dfrac{{7 \times 16}}{{9 \times 16}} = \dfrac{{112}}{{144}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{13}}{{16}} = \dfrac{{13 \times 9}}{{16 \times 9}} = \dfrac{{117}}{{144}}\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\) Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản sau đó quy đồng mẫu số ta được hai phân số lần lượt là \(\dfrac{{112}}{{144}}\)và \(\dfrac{{117}}{{144}}\).
|
.jpg)
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{{637}}{{741}} = \dfrac{{49}}{{...}}\)
