Trắc nghiệm: Viết các số đo độ dài dưới dạng số thập phân Toán 5Đề bài
Câu 1 :
Bạn An nói: Hai đơn vị đo độ dài liền nhau hơn kém nhau \(100\) lần. Bạn Bình nói: Mỗi đơn vị đo độ dài sẽ gấp \(10\) lần đơn vị bé hơn liền nó. Hỏi bạn nào nói đúng? A. Bạn An B. Bạn Bình C. Cả hai bạn đều nói sai D. Cả hai bạn đều nói đúng
Câu 2 :
Điền số thích hợp vào ô trống: \(3km\,9m = \) \(m\)
Câu 3 :
Chọn đáp án đúng để điền vào chỗ chấm: Viết số đo độ dài sau dưới dạng hỗn số có phần phân số là phân số tối giản: \(578m = ...hm\). A. \(5\dfrac{{78}}{{100}}\) B. \(57\dfrac{8}{{100}}\) C. \(5\dfrac{{39}}{{50}}\) D. \(57\dfrac{2}{{25}}\)
Câu 4 :
Viết số thập phân thích hợp vào ô trống (dạng gọn nhất): \(24m\,7dm = \) \(m\)
Câu 5 :
Viết số thập phân (gọn nhất) thích hợp vào ô trống: \(18km\,\,81m = \) \(km\).
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm: \(38317dm\,=\,... \, hm\). A. \(3,8317\) B. \(38,317\) C. \(383,17\) D. \(3831,7\)
Câu 7 :
Điền số thích hợp vào ô trống sau: \(53,2dm = \) \(dm\) \(cm\).
Câu 8 :
Điền số thích hợp vào ô trống: \(27,9{\rm{ }}km{\rm{ }} = \) \(m\).
Câu 9 :
Kéo thả dấu thích hợp vào ô trống:
\(>\)
\(=\)
\(<\)
\(72,5m\) ..... \(\,721,4dm\)
Câu 10 :
Trong cùng một thời gian Tom đi được quãng đường \(5km\,3m\), Jerry đi được quãng đường \(5,3km\). Hỏi bạn nào đi nhanh hơn? A. Bạn Tom B. Bạn Jerry C. Hai bạn đi nhanh như nhau.
Câu 11 :
Điền số thích hợp vào ô trống: Một hình vuông có chu vi là \(512cm.\) Vậy độ dài cạnh hình vuông đó là \(m.\)
Câu 12 :
Điền số thích hợp vào ô trống: Một hình chữ nhật có chu vi là \(336cm\). Biết chiều dài gấp đôi chiều rộng. Vậy chiều dài hình chữ nhật đó là \(km\). Chiều rộng hình chữ nhật đó là \(km\). Lời giải và đáp án
Câu 1 :
Bạn An nói: Hai đơn vị đo độ dài liền nhau hơn kém nhau \(100\) lần. Bạn Bình nói: Mỗi đơn vị đo độ dài sẽ gấp \(10\) lần đơn vị bé hơn liền nó. Hỏi bạn nào nói đúng? A. Bạn An B. Bạn Bình C. Cả hai bạn đều nói sai D. Cả hai bạn đều nói đúng Đáp án
B. Bạn Bình Phương pháp giải :
Dựa vào nhận xét, trong bảng đơn vị đo độ dài, hai đơn vị liền nhau hơn (kém) nhau \(10\) lần. Lời giải chi tiết :
Trong bảng đơn vị đo độ dài, hai đơn vị liền nhau hơn (kém) nhau \(10\) lần, tức là mỗi đơn vị đo độ dài sẽ gấp \(10\) lần đơn vị bé hơn liền nó. Vậy bạn An nói sai, bạn Bình nói đúng.
Câu 2 :
Điền số thích hợp vào ô trống: \(3km\,9m = \) \(m\) Đáp án
\(3km\,9m = \) \(m\) Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho: \(km\) và \(m\). - Tìm mối liên hệ giữa chúng: \(1{\rm{ }}km = 1000{\rm{ }}m\). - Đổi \(3km\) sang đơn vị đo là \(m\) rồi cộng thêm với \(9m\). Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có \(1{\rm{ }}km = 1000{\rm{ }}m\) nên \(3{\rm{ }}km = 3000{\rm{ }}m\). Do đó: \(3km\,9m = 3km + 9m = 3000m + 9m= 3009m\). Vậy đáp án đúng điền vào ô trống là \(3009\).
Câu 3 :
Chọn đáp án đúng để điền vào chỗ chấm: Viết số đo độ dài sau dưới dạng hỗn số có phần phân số là phân số tối giản: \(578m = ...hm\). A. \(5\dfrac{{78}}{{100}}\) B. \(57\dfrac{8}{{100}}\) C. \(5\dfrac{{39}}{{50}}\) D. \(57\dfrac{2}{{25}}\) Đáp án
C. \(5\dfrac{{39}}{{50}}\) Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho (\(hm\) và \(m\)) và tìm được mối liên hệ giữa chúng: \(1hm = 100m\) hay \(1m = \dfrac{1}{{100}}hm\) - Viết số đo độ dài đã cho thành số đo độ dài dưới dạng hỗn số có phần phân số là phân số thập phân. Rút gọn phần phân số của hỗn số vừa viết được thành phân số tối giản. Hỗn số viết được có đơn vị đo là \(hm\). Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có: \(1hm = 100m\) hay \(1m = \dfrac{1}{{100}}hm\). Do đó ta có: \(578m = 500m + 78m = 5hm + \dfrac{{78}}{{100}}hm = 5\dfrac{{78}}{{100}}hm = 5\dfrac{{39}}{{50}}hm\) Vậy \(578m = 5\dfrac{{39}}{{50}}hm\).
Câu 4 :
Viết số thập phân thích hợp vào ô trống (dạng gọn nhất): \(24m\,7dm = \) \(m\) Đáp án
\(24m\,7dm = \) \(m\) Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho (\(m\) và \(dm\)) và tìm mối liên hệ giữa chúng: \(1m = 10dm\) hay \(1dm = \dfrac{1}{{10}}m\). - Đổi số đo độ dài đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân dạng gọn nhất. Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có \(1m = 10dm\) hay\(1dm = \dfrac{1}{{10}}m\). Nên \(24m\,\,7dm = 24\dfrac{7}{{10}}m = 24,7m\) Vậy $24m\;{\rm{ 7}}dm = 24,7m$ Đáp án đúng điền vào ô trống là \(24,7\).
Câu 5 :
Viết số thập phân (gọn nhất) thích hợp vào ô trống: \(18km\,\,81m = \) \(km\). Đáp án
\(18km\,\,81m = \) \(km\). Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho (\(km\) và \(m\)) và tìm mối liên hệ giữa chúng: \(1km = 1000m\) hay \(1m = \dfrac{1}{{1000}}km\). - Đổi số đo độ dài đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân gọn nhất. Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có \(1km = 1000m\) hay \(1m = \dfrac{1}{{1000}}km\) Nên \(18km\,\,81m = 18\,\dfrac{{81}}{{1000}}km = 18,081km\). Vậy \(18km\,\,81m = 18,081km\). Đáp án đúng điền vào ô trống là \(18,081\).
Câu 6 :
Chọn số thích hợp để điền vào chỗ chấm: \(38317dm\,=\,... \, hm\). A. \(3,8317\) B. \(38,317\) C. \(383,17\) D. \(3831,7\) Đáp án
B. \(38,317\) Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho (\(hm\) và \(dm\)) và tìm mối liên hệ giữa chúng: \(1hm = 1000dm\) hay \(1dm = \dfrac{1}{{1000}}hm\). - Tách \(38317dm\,=\,38000dm\,+\,317dm\) rồi đổi số đo độ dài đã cho thành hỗn số có phần phân số là phân số thập phân. - Đổi hỗn số vừa tìm được thành số thập phân. Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có \(1hm = 1000dm\) hay \(1dm = \dfrac{1}{{1000}}hm\). Nên \(38317dm\,=\,38000dm\,+\,317dm\,=\,38hm\,\,317dm\,=\,38\dfrac{{317}}{{1000}}hm\,=\,38,317hm\) Vậy \(38317dm\,=\,38,317dm\).
Câu 7 :
Điền số thích hợp vào ô trống sau: \(53,2dm = \) \(dm\) \(cm\). Đáp án
\(53,2dm = \) \(dm\) \(cm\). Phương pháp giải :
- Xác định các đơn vị đo độ dài đã cho: \(dm;\,cm\). - Tách hỗn số thành phần nguyên và phần phân số, hai thành phần đều có đơn vị là \(dm.\) - Chuyển phần phân số với đơn vị là \(dm\) sang đơn vị \(cm\). Lời giải chi tiết :
Ta có: \(53,2dm = 53\dfrac{2}{{10}}dm = 53dm + \dfrac{2}{{10}}dm = 53dm+ 2cm = 53dm\;2cm\) Vậy \(53,2dm=53dm\;2cm\). Đáp án cần điền vào ô trống theo thứ tự từ trái qua phải là \(53;\,2\).
Câu 8 :
Điền số thích hợp vào ô trống: \(27,9{\rm{ }}km{\rm{ }} = \) \(m\). Đáp án
\(27,9{\rm{ }}km{\rm{ }} = \) \(m\). Phương pháp giải :
- Xác định hai đơn vị đo độ dài đã cho (\(km\) và \(m\)) và tìm được mối liên hệ giữa chúng: \(1km = 1000m\) hay \(1m = \dfrac{1}{{1000}}km\). - Viết số đo độ dài đã cho ra hỗn số có mẫu số ở phần phân số là \(10;{\rm{ }}100;{\rm{ }}1000…\) - Đổi hỗn số trên thành số đo độ dài có đơn vị là \(m\). Lời giải chi tiết :
Theo bảng đơn vị đo độ dài ta có \(1km = 1000m\) hay \(1m = \dfrac{1}{{1000}}km\) Nên \(27,9km = 27,900km = 27\dfrac{{900}}{{1000}}km = 27km + \dfrac{{900}}{{1000}}km = 27000m + 900m = 27900m\). Vậy đáp án đúng điền vào ô trống là \(27900\).
Câu 9 :
Kéo thả dấu thích hợp vào ô trống:
\(>\)
\(=\)
\(<\)
\(72,5m\) ..... \(\,721,4dm\) Đáp án
\(>\)
\(=\)
\(<\)
\(72,5m\)
\(>\) \(\,721,4dm\) Phương pháp giải :
- Xác định các số đo đã cùng đơn vị đo chưa, nếu không cùng đơn vị đo ta phải đổi thành cùng một đơn vị đo. - Xác định các phần nguyên và phần thập phân để so sánh bình thường như so sánh các số thập phân. Lời giải chi tiết :
Hai số đã cho không cùng đơn vị đo. Ta có: \(72,5m = 72\dfrac{5}{{10}}m = 72m + \dfrac{5}{{10}}m = 720dm + 5dm = 725dm\) So sánh hai số \(725dm\) và \(721,4dm\) ta thấy \(725 > 721,4\) (vì có phần nguyên \(725 > 721\)). Nên \(725dm > 721,4dm\), hay \(72,5m > 721,4dm\). Vậy đáp án đúng là dấu \( > \).
Câu 10 :
Trong cùng một thời gian Tom đi được quãng đường \(5km\,3m\), Jerry đi được quãng đường \(5,3km\). Hỏi bạn nào đi nhanh hơn? A. Bạn Tom B. Bạn Jerry C. Hai bạn đi nhanh như nhau. Đáp án
B. Bạn Jerry Phương pháp giải :
So sánh độ dài hai đoạn đường hai bạn đã đi bằng cách đưa độ dài quãng đường hai bạn đi được về cùng một đơn vị đo. Bạn nào đi quãng đường dài hơn bạn đó đi nhanh hơn. Lời giải chi tiết :
Ta thấy độ dài quãng đường hai bạn đi không cùng đơn vị đo. Ta có: +) \(5km\,3m{\rm{ }} = {\rm{ 5k}}m + 3m= 5000m + 3m = 5003m\). +) \(5,3km = 5,300km = 5\,\dfrac{{300}}{{1000}}km = 5km + \dfrac{{300}}{{1000}}km = 5000m + 300m = 5300m\). Mà \(5003m < 5300m\) nên \(5km\,3m < 5,3km\). Vậy bạn Jerry đi nhanh hơn bạn Tom.
Câu 11 :
Điền số thích hợp vào ô trống: Một hình vuông có chu vi là \(512cm.\) Vậy độ dài cạnh hình vuông đó là \(m.\) Đáp án
Một hình vuông có chu vi là \(512cm.\) Vậy độ dài cạnh hình vuông đó là \(m.\) Phương pháp giải :
- Tìm độ dài cạnh hình vuông ta lấy chu vi chia cho \(4\). - Đổi độ dài cạnh hình vuông từ \(cm\) sang đơn vị \(m\). Lời giải chi tiết :
Độ dài cạnh hình vuông đó là: \(512:4 = 128\;(cm)\) Ta có: \(128cm = 100cm + 28cm = 1m\;28cm = 1\dfrac{{28}}{{100}}m = 1,28m\) Vậy đáp án đúng điền vào ô trống là \(1,28\).
Câu 12 :
Điền số thích hợp vào ô trống: Một hình chữ nhật có chu vi là \(336cm\). Biết chiều dài gấp đôi chiều rộng. Vậy chiều dài hình chữ nhật đó là \(km\). Chiều rộng hình chữ nhật đó là \(km\). Đáp án
Một hình chữ nhật có chu vi là \(336cm\). Biết chiều dài gấp đôi chiều rộng. Vậy chiều dài hình chữ nhật đó là \(km\). Chiều rộng hình chữ nhật đó là \(km\). Phương pháp giải :
- Tìm nửa chu vi hình chữ nhật = chu vi \(:2\). Khi đó ta có tổng của chiều dài và chiều rộng và tỉ số của chiều dài, chiều rộng. Giải bài toán tìm hai số khi biết tổng và tỉ số ta tìm được chiều dài, chiều rộng hình chữ nhật. - Đổi độ dài chiều rộng hình chữ nhật từ \(cm\) sang đơn vị \(km\). - Đổi chiều dài hình chữ nhật từ đơn vị \(cm\) sang đơn vị \(km\). Lời giải chi tiết :
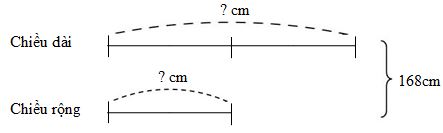
Nửa chu vi hình chữ nhật là: \(336:2 = 168(cm)\) Ta có sơ đồ:
Theo sơ đồ, tổng số phần bằng nhau là: \(1 + 2 = 3\) (phần) Giá trị một phần hay chiều rộng hình chữ nhật là: \(168:3 = 56\,(cm)\) Chiều dài hình chữ nhật là: \(56 \times 2 = 112\,(cm)\) Đổi: \(56cm = \dfrac{{56}}{{100000}}km = 0,00056km;\) \(112cm = \dfrac{{112}}{{100000}}km = 0,00112km \). Vậy đáp án cần điền vào ô trống theo thứ tự từ trên xuông dưới là \(0,00112;\,\,0,00056\).
|
.png)
.png)
.png)
.png)
