Trắc nghiệm: Luyện tập về diện tích các hình Toán 5Đề bài
Câu 1 :
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\). D. Cả A, B, C đều đúng.
Câu 2 :
Cho hình vẽ như bên dưới:
Biết hình chữ nhật \(ABCD\) có diện tích là \(1776c{m^2}\). Diện tích của hình tam giác \(MDC\) là: A. \(600c{m^2}\) B. \(750c{m^2}\) C. \(900c{m^2}\) D. \(1200c{m^2}\)
Câu 3 :
Điền số thích hợp vào ô trống: Cho hình vẽ như bên dưới:
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\). Vậy diện tích hình thang \(HBCD\) là \(d{m^2}\).
Câu 4 :
Tính diện tích phần được tô màu trong hình sau, biết khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\):
A. \(7,065c{m^2}\) B. \(21,195c{m^2}\) C. \(28,26c{m^2}\) D. \(35,325c{m^2}\)
Câu 5 :
Điền số thích hợp vào ô trống: Cho hình vẽ dưới đây:
Biết rằng \(ABCD\) là hình chữ nhật có \(AB = 35cm;\,\,BC = 18cm;\,\,AM = CP = \dfrac{1}{5}AB;\,\,BN = DQ = \dfrac{1}{3}BC\). Vậy diện tích hình bình hành \(MNPQ\) là \(c{m^2}\).
Câu 6 :
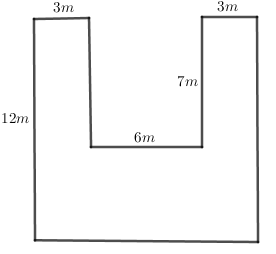
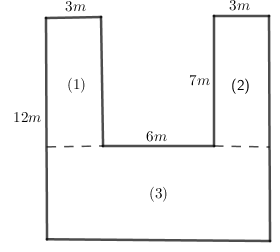
Tính diện tích mảnh đất có kích thước như hình vẽ:
A. \(60{m^2}\) B. \(102{m^2}\) C. \(132{m^2}\) D. \(144{m^2}\)
Câu 7 :
Điền số thích hợp vào ô trống: Một miếng bìa có hình dạng như hình vẽ dưới đây:
Vậy diện tích miếng bìa đó là \({cm^2}\).
Câu 8 :
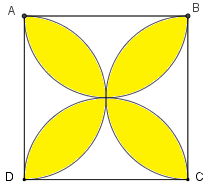
Cho hình vẽ như sau:
Tính diện tích phần tô màu trong hình vẽ, biết rằng hình vuông \(ABCD\) có cạnh dài $10cm$. A. \(5,375c{m^2}\) B. \(21,5c{m^2}\) C. \(38,5c{m^2}\) D. \(78,5c{m^2}\)
Câu 9 :
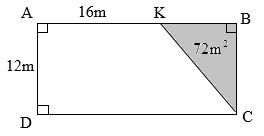
Điền số thích hợp vào ô trống: Một mảnh đất hình thang vuông có đáy bé là \(16m\), chiều cao là \(12m\). Người ta mở rộng mảnh đất hình thang về phía cạnh bên để có hình chữ nhật (xem hình vẽ bên dưới). Biết diện tích phần mở rộng (phần đã tô đậm) là \(72{m^2}\). Vậy diện tích mảnh đất hình thang vuông ban đầu là \({m^2}\).
Câu 10 :
Điền số thích hợp vào ô trống: Cho hình vẽ như bên dưới:
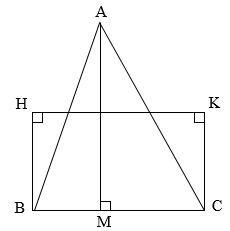
Biết rằng diện tích tam giác \(ABC\) bằng \(\dfrac{4}{5}\) diện tích hình chữ nhật \(HKCB\) và \(BC = 40cm\), độ dài cạnh \(BH\) bằng \(87,5\% \) độ dài cạnh \(BC\). Vậy chiều cao \(AM\) của tam giác \(ABC\) là \(cm\).
Câu 11 :
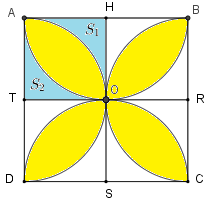
Tính diện tích bông hoa được tô màu trong hình vẽ sau, biết hình vuông \(ABCD\) có độ dài cạnh là \(6cm\).
A. \(5,13c{m^2}\) B. \(7,065c{m^2}\) C. \(20,52c{m^2}\) D. \(28,26c{m^2}\) Lời giải và đáp án
Câu 1 :
A. Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). B. Muốn tính diện tích hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). C. Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số \(3,14\). D. Cả A, B, C đều đúng. Đáp án
D. Cả A, B, C đều đúng. Phương pháp giải :
Dựa vào quy tắc tính diện tích các hình tam giác, hình thang, hình tròn. Lời giải chi tiết :
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho \(2\). Vậy cả A, B, C đều đúng.
Câu 2 :
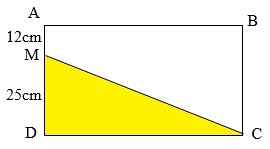
Cho hình vẽ như bên dưới:
Biết hình chữ nhật \(ABCD\) có diện tích là \(1776c{m^2}\). Diện tích của hình tam giác \(MDC\) là: A. \(600c{m^2}\) B. \(750c{m^2}\) C. \(900c{m^2}\) D. \(1200c{m^2}\) Đáp án
A. \(600c{m^2}\) Phương pháp giải :
- Tìm chiều rộng của hình chữ nhật : \(AD = 25cm + 12cm = 37cm\). - Tìm chiều dài của hình chữ nhật ta lấy diện tích chia cho chiều rộng. - Tam giác \(MDC\) là tam giác vuông nên để tìm diện tích ta tìm tích độ dài hai cạnh góc vuông rồi chia cho \(2\). Lời giải chi tiết :
Độ dài cạnh \(AD\) là: \(25cm + 12cm = 37\;(cm)\) Độ dài cạnh \(DC\) là: \(1776:37 = 48\;(cm)\) Diện tích tam giác \(MDC\) là: \(25 \times 48:2 = 600\;(c{m^2})\) Đáp số: \(600c{m^2}\).
Câu 3 :
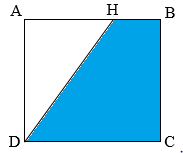
Điền số thích hợp vào ô trống: Cho hình vẽ như bên dưới:
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\). Vậy diện tích hình thang \(HBCD\) là \(d{m^2}\). Đáp án
Cho hình vẽ như bên dưới:
Biết hình vuông \(ABCD\) có diện tích là \(2500d{m^2}\), độ dài cạnh \(AH\) bằng \(70\% \) độ dài đoạn \(AB\). Vậy diện tích hình thang \(HBCD\) là \(d{m^2}\). Phương pháp giải :
- Tìm độ dài cạnh hình vuông. - Tìm độ dài các cạnh đáy và chiều cao của hình thang sau đó để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho \(2\). Lời giải chi tiết :
Ta có \(50 \times 50 = 2500\). Vậy độ dài cạnh hình vuông \(ABCD\) là \(50dm\) hay \(AB = BC = CD = AD = 50dm\). Ta có \(HBCD\) là hình thang vuông với chiều cao là cạnh \(BC\), hai đáy là \(HB,\,\,DC\). Độ dài cạnh \(AH\) là: \(50:100 \times 70 = 35\;(dm)\) Độ dài cạnh \(HB\) là: \(50 - 35 = 15\;(dm)\) Diện tích hình thang \(HBCD\) là: \((15 + 50) \times 50:2 = 1625\;(d{m^2})\) Đáp số: \(1625d{m^2}\). Vậy đáp án đúng điền vào ô trống là \(1625\).
Câu 4 :
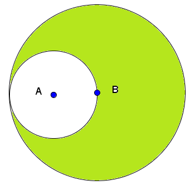
Tính diện tích phần được tô màu trong hình sau, biết khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\):
A. \(7,065c{m^2}\) B. \(21,195c{m^2}\) C. \(28,26c{m^2}\) D. \(35,325c{m^2}\) Đáp án
B. \(21,195c{m^2}\) Phương pháp giải :
- Xác định bán kính của hai hình tròn: hình tròn tâm \(A\) có bán kính là \(AB = 1,5cm\) và hình tròn tâm \(B\) có bán kính là \(1,5 \times 2 = 3cm\). - Tính diện tích của hai hình tròn theo công thức: \(S = r \times r \times 3,14\). - Tính diện tích phần tô màu ta lấy diện tích hình tròn tâm \(B\) trừ đi diện tích hình tròn tâm \(A\). Lời giải chi tiết :
Khoảng cách từ tâm \(A\) đến tâm \(B\) là \(1,5cm\) nên ta có \(AB = 1,5cm\). \(AB\) chính là bán kính của hình tròn tâm \(A\), vậy hình tròn tâm \(A\) có bán kính là \(1,5cm\). Hình tròn tâm \(B\) có bán kính chính là đường kính của hình tròn tâm \(A\). Vậy hình tròn tâm \(B\) có bán kính là: \(1,5 \times 2 = 3 \;(cm)\) Diện tích của hình tròn tâm \(A\) là: \(1,5 \times 1,5 \times 3,14 = 7,065\;(c{m^2})\) Diện tích của hình tròn tâm \(B\) là: \(3 \times 3 \times 3,14 = 28,26\;(c{m^2})\) Diện tích của phần được tô màu là: \(28,26 - 7,065 = 21,195\;(c{m^2})\) Đáp số: \(21,195c{m^2}\).
Câu 5 :
Điền số thích hợp vào ô trống: Cho hình vẽ dưới đây:
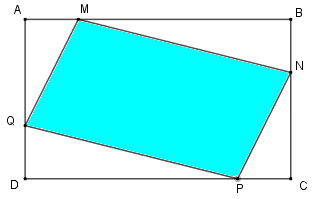
Biết rằng \(ABCD\) là hình chữ nhật có \(AB = 35cm;\,\,BC = 18cm;\,\,AM = CP = \dfrac{1}{5}AB;\,\,BN = DQ = \dfrac{1}{3}BC\). Vậy diện tích hình bình hành \(MNPQ\) là \(c{m^2}\). Đáp án
Cho hình vẽ dưới đây:
Biết rằng \(ABCD\) là hình chữ nhật có \(AB = 35cm;\,\,BC = 18cm;\,\,AM = CP = \dfrac{1}{5}AB;\,\,BN = DQ = \dfrac{1}{3}BC\). Vậy diện tích hình bình hành \(MNPQ\) là \(c{m^2}\). Phương pháp giải :
Diện tích hình bình hành \(MNPQ\) bằng diện tích hình chữ nhật \(ABCD\) trừ đi tổng diện tích của bốn hình tam giác vuông \(AMQ,\,\,BMN,\,\,CPN,\,\,DPQ\). Lời giải chi tiết :
Theo đề bài ta có: \(\begin{array}{l}AM = CP = 35:5 = 7cm\\BN = DQ = 18:3 = 6cm\end{array}\) Từ đó ta có: \(\begin{array}{l}BM = DP = 35 - 7 = 28cm\\AQ = CN = 18 - 6 = 12cm\end{array}\) Diện tích tam giác \(AMQ\) là : \(7 \times 12:2 = 42 \; (c{m^2})\) Diện tích tam giác \(BMN\) là : \(28 \times 6:2 = 84 \;(c{m^2})\) Diện tích tam giác \(\,CPN\) là : \(7 \times 12:2 = 42 \;(c{m^2})\) Diện tích tam giác \(DPQ\) là : \(28 \times 6:2 = 84 \;(c{m^2})\) Diện tích hình chữ nhật \(ABCD\) là : \(35 \times 18 = 630 \;(c{m^2})\) Diện tích hình bình hành \(MNPQ\) là: \(630 - (42 + 84 + 42 + 84) = 378 \;(c{m^2})\) Đáp số: \(378c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(378\).
Câu 6 :
Tính diện tích mảnh đất có kích thước như hình vẽ:
A. \(60{m^2}\) B. \(102{m^2}\) C. \(132{m^2}\) D. \(144{m^2}\) Đáp án
B. \(102{m^2}\) Phương pháp giải :
Chia mảnh đất đã cho thành các mảnh đất nhỏ mà có thể dễ dàng tính được diện tích các mảnh đó. Diện tích mảnh đất ban đầu bằng tổng diện tích các mảnh đất nhỏ. Lời giải chi tiết :
Chia mảnh đất đã cho thành \(3\) mảnh đất hình chữ nhật như sau:
Gọi \(S\) là diện tích mảnh đất ban đầu, \({S_1},\,\,{S_2},\,\,{S_3}\) lần lượt là diện tích các mảnh đất \((1),\,(2),\,(3)\). Khi đó: \(S = {S_1} + {S_2} + {S_3}\). Diện tích mảnh đất thứ nhất là: \(7 \times 3 = 21\;({m^2})\) Diện tích mảnh đất thứ hai là: \(7 \times 3 = 21\;({m^2})\) Chiều rộng của mảnh đất thứ ba là: \(12 - 7 = 5\;(m)\) Chiều dài của mảnh đất thứ ba là: \(3 + 6 + 3 = 12\;(m)\) Diện tích mảnh đất thứ ba là: $12 \times 5 = 60\;({m^2})$ Diện tích mảnh đất ban đầu là: \(21 + 21 + 60 = 102\;({m^2})\) Đáp số: \(102{m^2}\).
Câu 7 :
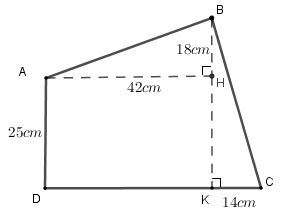
Điền số thích hợp vào ô trống: Một miếng bìa có hình dạng như hình vẽ dưới đây:
Vậy diện tích miếng bìa đó là \({cm^2}\). Đáp án
Một miếng bìa có hình dạng như hình vẽ dưới đây:
Vậy diện tích miếng bìa đó là \({cm^2}\). Phương pháp giải :
Diện tích miếng bìa \(ABCD\) bằng tổng diện tích của hai miếng bìa hình tam giác \(ABH,\,\,BKC\) và miếng bìa hình chữ nhật \(AHKD\). Lời giải chi tiết :
Diện tích miếng bìa hình tam giác \(ABH\) là: \(42 \times 18:2 = 378 \; (c{m^2})\) Độ dài đoạn \(BK\) là: \(18 + 25 = 43\;(cm)\) Diện tích miếng bìa hình tam giác \(BKC\) là: \(43 \times 14:2 = 301\; (c{m^2})\) Diện tích miếng bìa hình chữ nhật \(AHKD\) là: \(42 \times 25 = 1050\; (c{m^2})\) Diện tích miếng bìa \(ABCD\) là : \(378 + 301 + 1050 = 1729 \;(c{m^2})\) Đáp số: \(1729c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(1729\).
Câu 8 :
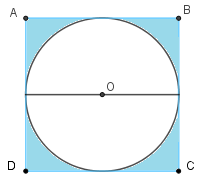
Cho hình vẽ như sau:
Tính diện tích phần tô màu trong hình vẽ, biết rằng hình vuông \(ABCD\) có cạnh dài $10cm$. A. \(5,375c{m^2}\) B. \(21,5c{m^2}\) C. \(38,5c{m^2}\) D. \(78,5c{m^2}\) Đáp án
B. \(21,5c{m^2}\) Phương pháp giải :
- Hình tròn tâm \(O\) có đường kính bằng độ dài cạnh hình vuông. Từ đó ta tìm được bán kính hình tròn, sau đó tính diện tích hinh tròn theo công thức \(S = r \times r \times 3,14\). - Tính diện tích hình vuông. - Diện tích phần tô màu bằng diện tích hình vuông trừ đi diện tích hình tròn tâm \(O\). Lời giải chi tiết :
Hình tròn tâm \(O\) có đường kính bằng độ dài cạnh hình vuông và bằng \(10cm\). Bán kính của hình tròn tâm \(O\) là: \(10:2 = 5\;(cm)\) Diện tích hình tròn tâm \(O\) là: \(5 \times 5 \times 3,14 = 78,5\;(c{m^2})\) Diện tích hình vuông \(ABCD\) là: \(10 \times 10 = 100\;(c{m^2})\) Diện tích phần tô màu là: \(100 - 78,5 = 21,5\;(c{m^2})\) Đáp số: \(21,5c{m^2}\).
Câu 9 :
Điền số thích hợp vào ô trống: Một mảnh đất hình thang vuông có đáy bé là \(16m\), chiều cao là \(12m\). Người ta mở rộng mảnh đất hình thang về phía cạnh bên để có hình chữ nhật (xem hình vẽ bên dưới). Biết diện tích phần mở rộng (phần đã tô đậm) là \(72{m^2}\). Vậy diện tích mảnh đất hình thang vuông ban đầu là \({m^2}\).
Đáp án
Một mảnh đất hình thang vuông có đáy bé là \(16m\), chiều cao là \(12m\). Người ta mở rộng mảnh đất hình thang về phía cạnh bên để có hình chữ nhật (xem hình vẽ bên dưới). Biết diện tích phần mở rộng (phần đã tô đậm) là \(72{m^2}\). Vậy diện tích mảnh đất hình thang vuông ban đầu là \({m^2}\).
Phương pháp giải :
Muốn tính được diện tích hình thang vuông ta phải tìm được đáy lớn \(DC\). - Diện tích phần mở rộng là diện tích hình tam giác có chiều cao bằng \(12m\) (bằng chiều cao hình thang) từ đó ta tìm được đáy \(BK\). - Tìm độ dài \(AB\): \(AB = AK + KB\) - \(ABCD\) là hình chữ nhật nên \(AB = CD\) - Tính diện tích mảnh đất hình thang ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\). Lời giải chi tiết :
Diện tích phần đất mở rộng chính là diện tích của mảnh đất hình tam giác vuông \(KBC\) có chiều cao \(BC\) bằng \(12m\) (bằng chiều cao của hình thang). Độ dài cạnh \(KB\) là: \(72 \times 2:12 = 12\;(m)\) Độ dài cạnh \(AB\) là: \(16 + 12 = 28\;(m)\) Vì \(ABCD\) là hình chữ nhật nên \(AB = CD = 28cm\). Diện tích mảnh đất hình thang vuông ban đầu là: \((16 + 28) \times 12:2 = 264\;({m^2})\) Đáp số: \(264{m^2}\). Vậy đáp án đúng điền vào ô trống là \(264\).
Câu 10 :
Điền số thích hợp vào ô trống: Cho hình vẽ như bên dưới:
Biết rằng diện tích tam giác \(ABC\) bằng \(\dfrac{4}{5}\) diện tích hình chữ nhật \(HKCB\) và \(BC = 40cm\), độ dài cạnh \(BH\) bằng \(87,5\% \) độ dài cạnh \(BC\). Vậy chiều cao \(AM\) của tam giác \(ABC\) là \(cm\). Đáp án
Cho hình vẽ như bên dưới:
Biết rằng diện tích tam giác \(ABC\) bằng \(\dfrac{4}{5}\) diện tích hình chữ nhật \(HKCB\) và \(BC = 40cm\), độ dài cạnh \(BH\) bằng \(87,5\% \) độ dài cạnh \(BC\). Vậy chiều cao \(AM\) của tam giác \(ABC\) là \(cm\). Phương pháp giải :
- Tính độ dài chiều rộng \(BH\) ta lấy độ dài cạnh \(BC\) chia cho \(100\) rồi nhân với \(87,5\). - Tính diện tích hình chữ nhật \(HKCB\). - Tính diện tích tam giác \(ABC\) ta lấy diện tích hình chữ nhật \(HKCB\) nhân với \(\dfrac{4}{5}\). - Tính chiều cao \(AH\) ta lấy diện tích tam giác \(ABC\) nhân với \(2\) rồi chia cho độ dài đáy \(BC\). Lời giải chi tiết :
Độ dài cạnh \(BH\) là: \(40:100 \times 87,5 = 35 \;(cm)\) Diện tích hình chữ nhật \(HKCB\) là: \(40 \times 35 = 1400\;(c{m^2})\) Diện tích tam giác \(ABC\) là: \(1400 \times \dfrac{4}{5} = 1120\;(c{m^2})\) Chiều cao \(AH\) là: \(1120 \times 2:40 = 56\;(cm)\) Đáp số: \(56cm\). Vậy đáp án đúng điền vào ô trống là \(56\).
Câu 11 :
Tính diện tích bông hoa được tô màu trong hình vẽ sau, biết hình vuông \(ABCD\) có độ dài cạnh là \(6cm\).
A. \(5,13c{m^2}\) B. \(7,065c{m^2}\) C. \(20,52c{m^2}\) D. \(28,26c{m^2}\) Đáp án
C. \(20,52c{m^2}\) Phương pháp giải :
- Gọi \(H,R,S,T\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA\) và \(O\) là giao điểm của hai cạnh \(HS\) và \(RT\). Ta chia hình vuông ban đầu thành \(4\) hình vuông bằng nhau có cạnh là \(3cm\) (xem hình vẽ ở bài giải). - Tính diện tích hình vuông \(AHOT\). - Diện tích phần \({S_1}\) bằng diện tích hình vuông \(AHOT\) trừ đi \(\dfrac{1}{4}\) diện tích hình tròn tâm \(T\) bán kính \(3cm\). - Diện tích phần \({S_2}\) bằng diện tích phần \({S_1}\). - Diện tích một cánh hoa bằng diện tích hình vuông \(AHOT\) trừ đi tổng diện tích hai phần \({S_1}\) và \({S_2}\). - Diện tích bông hoa được tô màu bằng diện tích một cánh hoa nhân với \(4\) (do \(4\) cánh hoa có diện tích bằng nhau). Lời giải chi tiết :
Gọi \(H,R,S,T\) lần lượt là trung điểm của các cạnh \(AB,BC,CD,DA\) và \(O\) là giao điểm của hai cạnh \(HS\) và \(RT\). Ta chia hình vuông ban đầu thành \(4\) hình vuông bằng nhau như hình vẽ.
Độ dài cạnh của mỗi hình vuông nhỏ là: \(6:2 = 3\;(cm)\) Nhận xét rằng diện tích \(4\) hình vuông nhỏ đều bằng nhau, \(2\) phần không được tô màu ở mỗi hình vuông nhỏ đều bằng nhau và diện tích mỗi cánh hoa đều bằng nhau. Diện tích hình vuông \(AHOT\) là: \(3 \times 3 = 9\;(c{m^2})\) Diện tích hình tròn tâm \(T\) bán kính \(3cm\) là: \(3 \times 3 \times 3,14 = 28,26\;(c{m^2})\) \(\dfrac{1}{4}\) diện tích của hình tròn tâm \(T\) bán kính \(3cm\) là: \(28,26 \times \dfrac{1}{4} = 7,065\;(c{m^2})\) Diện tích phần \({S_1}\) là: \(9 - 7,065 = 1,935\;(c{m^2})\) Ta có phần \({S_1}\) và phần \({S_2}\) có diện tích bằng nhau và bằng \(1,935c{m^2}\). Diện tích \(1\) cánh hoa là: \(9 - (1,935 + 1,935) = 5,13\;(c{m^2})\) Diện tích bông hoa được tô màu là: \(5,13 \times 4 = 20,52\;(c{m^2})\) Đáp số: \(20,52c{m^2}\).
|
.jpg)
