Trắc nghiệm: Hình tam giác. Diện tích hình tam giác Toán 5Đề bài
Câu 1 :
A. \(3\) cạnh B. \(3\) góc C. \(3\) đỉnh D. Cả A, B, C đều đúng
Câu 2 :
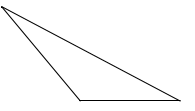
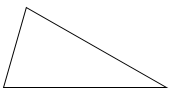
Hình tam giác có ba góc nhọn. Hình tam giác có một góc vuông và hai góc nhọn Hình tam giác có một góc tù và hai góc nhọn.
Câu 3 :
Cho hình vẽ như bên dưới:
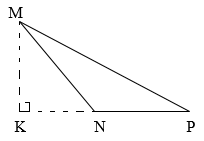
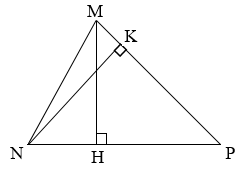
Trong tam giác \(MNP\), \(MK\) là chiều cao tương ứng với: A. Cạnh \(MN\) B. Cạnh \(NP\) C. Cạnh \(MP\) D. Cạnh \(KN\)
Câu 4 :
Điền số thích hợp vào ô trống: Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là \(c{m^2}.\)
Câu 5 :
Tính diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là \(27dm\). A. \(67,5\,d{m^2}\) B. \(67,5\,{m^2}\) C. \(675\,d{m^2}\) D. \(675\,{m^2}\)
Câu 6 :
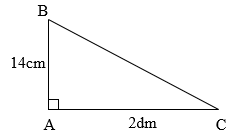
Tính diện tích tam giác vuông \(ABC\) có kích thước như hình vẽ bên dưới:
A. \(140\,c{m^2}\) B. \(280\,d{m^2}\) C. \(14\,d{m^2}\) D. \(28\,c{m^2}\)
Câu 7 :
A. \(17,5cm\) B. \(23,5cm\) C. \(35cm\) D. \(396cm\)
Câu 8 :
Một hình tam giác có diện tích là \(8{m^2}\) và độ dài cạnh đáy là \(32dm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(dm\).
Câu 9 :
Cho hình vẽ như bên dưới:
Tính diện tích hình tam giác \(HDC\). Biết hình chữ nhật \(ABCD\) có \(AB = 37cm,\,\,BC = 24cm\) A. \(444c{m^2}\) B. \(888c{m^2}\) C. \(1234c{m^2}\) D. \(1776c{m^2}\)
Câu 10 :
Một miếng đất hình chữ nhật có chu vi là \(86m\), chiều dài $28m$. Ở giữa miếng đất, người ta làm một bồn hoa hình tam giác có chiều cao $9,6m$ và bằng $\dfrac{3}{5}$ cạnh đáy. Vậy diện tích miếng đất còn lại là \({m^2}.\)
Câu 11 :
Tính diện tích hình tam giác \(AHK\). Biết hình vuông \(ABCD\) có cạnh \(16cm\) và \(BK = KC,\,\,DH = HC\).
A. \(156c{m^2}\) B. \(128c{m^2}\) C. \(96c{m^2}\) D. \(64c{m^2}\)
Câu 12 :
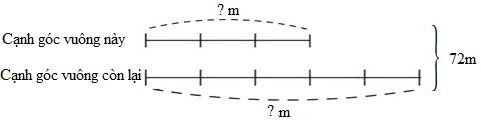
Một thửa ruộng hình tam giác vuông có tổng hai cạnh góc vuông là $72m$ và cạnh góc vuông này bằng $0,6$ lần cạnh góc vuông kia. Trên thửa ruộng này người ta trồng lúa, trung bình cứ \(100m^2\) thu được $60kg$ thóc. Hỏi trên cả thửa ruộng, người ta thu hoạch được bao nhiêu tạ thóc? A. \(3,645\) tạ B. \(7,29\) tạ C. \(364,5\) tạ D. \(729\) tạ
Câu 13 :
Cho tam giác \(MNP\) có \(MP = 32cm,\,NP = 36cm\). Biết chiều cao tương ứng với đáy \(NP\) là \(MH = 24cm\). Vậy chiều cao tương ứng với đáy \(MP\) là \(NK = \) \(cm\).
Câu 14 :
A. \(569,5d{m^2}\) B. \(1139d{m^2}\) C. \(1394d{m^2}\) D. \(2278d{m^2}\) Lời giải và đáp án
Câu 1 :
A. \(3\) cạnh B. \(3\) góc C. \(3\) đỉnh D. Cả A, B, C đều đúng Đáp án
D. Cả A, B, C đều đúng Phương pháp giải :
Dựa vào cấu trúc của một tam giác. Lời giải chi tiết :
Một tam giác có \(3\) cạnh, \(3\) góc và \(3\) đỉnh. Vậy cả A, B, C đều đúng.
Câu 2 :
Hình tam giác có ba góc nhọn. Hình tam giác có một góc vuông và hai góc nhọn Hình tam giác có một góc tù và hai góc nhọn. Đáp án
Hình tam giác có một góc vuông và hai góc nhọn
Hình tam giác có một góc tù và hai góc nhọn.
Hình tam giác có ba góc nhọn. Phương pháp giải :
Quan sát các góc trong một tam giác để mô ta tam giác đã cho. Lời giải chi tiết :
Quan sát các tam giác theo thứ tự từ trên xuống dưới ta có: - Hình tam giác thứ nhất có một góc vuông và hai góc nhọn - Hình tam giác thứ hai có một góc tù và hai góc nhọn. - Hình tam giác thứ ba có ba góc nhọn.
Câu 3 :
Cho hình vẽ như bên dưới:
Trong tam giác \(MNP\), \(MK\) là chiều cao tương ứng với: A. Cạnh \(MN\) B. Cạnh \(NP\) C. Cạnh \(MP\) D. Cạnh \(KN\) Đáp án
B. Cạnh \(NP\) Phương pháp giải :
Trong hình tam giác, độ dài đoạn thẳng từ đỉnh vuông góc với đáy tương ứng gọi là chiều cao của hình tam giác. Lời giải chi tiết :
Hình tam giác \(MNP\) có \(MK\) vuông góc với \(NP \), do đó \(MK\) là chiều cao tương ứng với cạnh đáy \(NP\).
Câu 4 :
Điền số thích hợp vào ô trống: Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là \(c{m^2}.\) Đáp án
Diện tích hình tam giác có độ dài đáy là \(25cm\) và chiều cao là \(16cm\) là \(c{m^2}.\) Phương pháp giải :
Độ dài đáy và chiều cao đã có cùng đơn vị đo nên để tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho \(2\). Lời giải chi tiết :
Diện tích tam giác đó là: \(\dfrac{{25 \times 16}}{2} = 200\left( {c{m^2}} \right)\) Đáp số: \(200c{m^2}\). Vậy đáp án đúng điền vào ô trống là \(200\).
Câu 5 :
Tính diện tích hình tam giác có độ dài đáy là \(5m\) và chiều cao là \(27dm\). A. \(67,5\,d{m^2}\) B. \(67,5\,{m^2}\) C. \(675\,d{m^2}\) D. \(675\,{m^2}\) Đáp án
C. \(675\,d{m^2}\) Phương pháp giải :
Độ dài đáy và chiều cao chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, \(5m = 50dm\), sau đó tính diện tích ta lấy độ dài đáy nhân với chiều cao rồi chia cho \(2\). Lời giải chi tiết :
Đổi \(5m = 50dm\) Diện tích tam giác đó là: \(\dfrac{{50 \times 27}}{2} = 675\left( {d{m^2}} \right)\) Đáp số: \(675d{m^2}\)
Câu 6 :
Tính diện tích tam giác vuông \(ABC\) có kích thước như hình vẽ bên dưới:
A. \(140\,c{m^2}\) B. \(280\,d{m^2}\) C. \(14\,d{m^2}\) D. \(28\,c{m^2}\) Đáp án
A. \(140\,c{m^2}\) Phương pháp giải :
Muốn tính diện tích tam giác vuông ta lấy độ dài hai cạnh góc vuông nhân với nhau (cùng một đơn vị đo) rồi chia cho \(2\). Lời giải chi tiết :
Đổi \(2dm = 20cm\) Diện tích tam giác vuông \(ABC\) là: \(\dfrac{{14 \times 20}}{2} = 140\left( {c{m^2}} \right)\) Đáp số: \(140c{m^2}\). Chú ý
Nếu hai cạnh góc vuông chưa cùng đơn vị đo thì ta phải đổi về cùng đơn vị đo rồi sau đó tính diện tích.
Câu 7 :
A. \(17,5cm\) B. \(23,5cm\) C. \(35cm\) D. \(396cm\) Đáp án
C. \(35cm\) Phương pháp giải :
Từ công thức tính diện tích hình tam giác: \(S = \dfrac{{a \times h}}{2}\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S \times 2:h\). Lời giải chi tiết :
Độ dài cạnh đáy của hình tam giác đó là: \(420 \times 2:24 = 35\,\,(cm)\) Đáp số: \(35cm\).
Câu 8 :
Một hình tam giác có diện tích là \(8{m^2}\) và độ dài cạnh đáy là \(32dm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(dm\). Đáp án
Một hình tam giác có diện tích là \(8{m^2}\) và độ dài cạnh đáy là \(32dm\). Vậy chiều cao tương ứng với cạnh đáy đó là \(dm\). Phương pháp giải :
- Đổi \(8{m^2}\) sang đơn vị đo là \(d{m^2}\) . - Từ công thức tính diện tích hình tam giác: \(S = \dfrac{{a \times h}}{2}\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S \times 2:a\) . Lời giải chi tiết :
Đổi \(8{m^2} = 800d{m^2}\) Chiều cao của tam giác đó là: \(800 \times 2:32 = 50\,\,(dm)\) Đáp số: \(50dm\). Vậy đáp án đúng điền vào ô trống là \(50\). Chú ý
Đơn vị đo của diện tích phải tương ứng với đơn vị đo của độ dài đáy và chiều cao. Độ dài cạnh đáy và chiều cao có đơn vị đo là \(dm\) thì đơn vị đo của diện tích phải \(d{m^2}\). Vì thế để giải được bài toán này ta cần đổi diện tích sang đơn vị đo là \(d{m^2}\) rồi mới thay số vào công thức để tính chiều cao.
Câu 9 :
Cho hình vẽ như bên dưới:
Tính diện tích hình tam giác \(HDC\). Biết hình chữ nhật \(ABCD\) có \(AB = 37cm,\,\,BC = 24cm\) A. \(444c{m^2}\) B. \(888c{m^2}\) C. \(1234c{m^2}\) D. \(1776c{m^2}\) Đáp án
A. \(444c{m^2}\) Phương pháp giải :
- Kẻ \(HK\) vuông góc với \(CD\), khi đó \(HK\) là chiều cao tương ứng với cạnh đáy \(CD\). Ta có chiều cao \(HK\) bằng chiều rộng của hình chữ nhật \(ABCD\): \(HK = BC = 24cm\). - \(ABCD\) là hình chữ nhật nên \(CD = AB = 37cm\). - Tính diện tích tam giác \(HCD\) theo công thức: \(S = a \times h:2\). Lời giải chi tiết :
Kẻ \(HK\) vuông góc với \(CD\), khi đó \(HK\) là chiều cao tương ứng với cạnh đáy \(CD\). Ta có chiều cao \(HK\) bằng chiều rộng của hình chữ nhật \(ABCD\) hay \(HK = BC = 24cm\) Vì \(ABCD\) là hình chữ nhật nên \(CD = AB = 37cm\). Diện tích tam giác \(HDC\) là: \(37 \times 24:2 = 444\left( {c{m^2}} \right)\) Đáp số: \(444c{m^2}\).
Câu 10 :
Một miếng đất hình chữ nhật có chu vi là \(86m\), chiều dài $28m$. Ở giữa miếng đất, người ta làm một bồn hoa hình tam giác có chiều cao $9,6m$ và bằng $\dfrac{3}{5}$ cạnh đáy. Vậy diện tích miếng đất còn lại là \({m^2}.\) Đáp án
Một miếng đất hình chữ nhật có chu vi là \(86m\), chiều dài $28m$. Ở giữa miếng đất, người ta làm một bồn hoa hình tam giác có chiều cao $9,6m$ và bằng $\dfrac{3}{5}$ cạnh đáy. Vậy diện tích miếng đất còn lại là \({m^2}.\) Phương pháp giải :
- Tìm nửa chu vi ta lấy chu vi chia cho \(2\). - Tìm chiều rộng miếng đất theo công thức: chiều rộng = nửa chu vi – chiều dài. - Tính diện tích miếng đất hình chữ nhật theo công thức: Diện tích = chiều dài × chiều rộng. - Tính cạnh đáy của bồn hoa: \(9,6:3 \times 5 = 16m\) - Tính diện tích bồn hoa theo công thức: \(S = a \times h:2\) - Tính diện tích miếng đất còn lại ta lấy diên tích miếng đất hình chữ nhật trừ đi diện tích bồn hoa. Lời giải chi tiết :
Nửa chu vi miếng đất hình chữ nhật đó là: \(86:2 = 43\;(m)\) Chiều rộng miếng đất đó là: \(43 - 28 = 15\;(m)\) Diện tích miếng đất hình chữ nhật đó là: \(28 \times 15 = 420\,\left( {c{m^2}} \right)\) Độ dài cạnh đáy của bồn hoa là: \(9,6:3 \times 5 = 16\;(m)\) Diện tích bồn hoa hình tam giác đó là: \(16 \times 9,6:2 = 76,8\,\left( {{m^2}} \right)\) Diện tích miếng đất còn lại là: \(420 - 76,8 = 343,2\,\left( {{m^2}} \right)\) Đáp số: \(343,2{m^2}\). Vậy đáp án đúng điền vào ô trống là \(343,2\). Chú ý
- Cần nhớ các công thức tính diện tích hình chữ nhật và diện tích tam giác. - Khi tính chiều rộng hình chữ nhật một số học sinh lấy chu vi trừ đi chiều dài, từ đó tìm diện tích sai.
Câu 11 :
Tính diện tích hình tam giác \(AHK\). Biết hình vuông \(ABCD\) có cạnh \(16cm\) và \(BK = KC,\,\,DH = HC\).
A. \(156c{m^2}\) B. \(128c{m^2}\) C. \(96c{m^2}\) D. \(64c{m^2}\) Đáp án
C. \(96c{m^2}\) Phương pháp giải :
Muốn tính diện tích hình tam giác \(AHK\) ta lấy diện tích hình vuông \(ABCD\) trừ đi tổng diện tích của ba hình tam giác vuông \(ABK,\,\,KCH\) và \(ADH\). Lời giải chi tiết :
Ta có \(ABCD\) là hình vuông cạnh \(16cm\) nên \(AB = BC = CD = AD = 16cm\). Lại có theo đề bài \(BK = KC,\,\,DH = HC\) nên \(BK = KC = \,DH = HC = 16:2 = 8cm\). Diện tích hình vuông \(ABCD\) là: \(16 \times 16 = 256\;(c{m^2})\) Diện tích hình tam giác \(ABK\) là: \(16 \times 8:2 = 64\;(c{m^2})\) Diện tích hình tam giác \(KCH\) là: \(8 \times 8:2 = 32\;(c{m^2})\) Diện tích hình tam giác \(ADH\) là: \(16 \times 8:2 = 64\;(c{m^2})\) Diện tích hình tam giác \(AHK\) là: \(256 - (64 + 32 + 64) = 96\;(c{m^2})\) Đáp số: \(96c{m^2}\).
Câu 12 :
Một thửa ruộng hình tam giác vuông có tổng hai cạnh góc vuông là $72m$ và cạnh góc vuông này bằng $0,6$ lần cạnh góc vuông kia. Trên thửa ruộng này người ta trồng lúa, trung bình cứ \(100m^2\) thu được $60kg$ thóc. Hỏi trên cả thửa ruộng, người ta thu hoạch được bao nhiêu tạ thóc? A. \(3,645\) tạ B. \(7,29\) tạ C. \(364,5\) tạ D. \(729\) tạ Đáp án
A. \(3,645\) tạ Phương pháp giải :
- Đổi \(0,6 = \dfrac{3}{5}\). Khi đó ta có bài toán tổng tỉ cơ bản. Giải bài toán này ta tìm được độ dài hai cạnh góc vuông, từ đó tính được diện tích thửa ruộng. - Tìm số thóc thu được theo bài toán tỉ lệ thuận: tìm tỉ số giữa diện tích và \(100m^2\), diện tích gấp \(100m^2\) bao nhiêu lần thì số thóc thu được cũng gấp \(60kg\) bấy nhiêu lần. - Đổi số ki-lô-gam thóc thu được ra đơn vị là tạ. Lời giải chi tiết :
Đổi \(0,6 = \dfrac{3}{5}\) Ta có sơ đồ:
Tổng số phần bằng nhau là : \(3 + 5 = 8\) (phần) Giá trị một phần là: \(72:8 = 9\;(m)\) Độ dài một cạnh góc vuông là: \(9 \times 3 = 27\;(m)\) Độ dài cạnh góc vuông còn lại là: \(72 - 27 = 45\;(m)\) Diện tích thửa ruộng đó là: \(45 \times 27:2 = 607,5\;({m^2})\) \(607,5m^2\) gấp \(100m^2\) số lần là: $607,5:100 = 6,075$ (lần) Trên cả thửa ruộng, người ta thu hoạch được số thóc là: \(60 \times 6,075 = 364,5\;(kg)\) \(364,5kg = 3,645\) tạ Đáp số: \(3,645\) tạ. Chọn A Chú ý
- Cần nhớ phương pháp giải bài toán tổng tỉ và bài toán về hai đại lượng tỉ lệ thuận. - Cần nhớ bảng đơn vị đo khối lượng và cách viết số đo khối lượng dưới dạng số thập phân. - Bước cuối tìm số thóc thu được ta có thể làm gộp thành một bước: \(607,5:100 \times 60\).
Câu 13 :
Cho tam giác \(MNP\) có \(MP = 32cm,\,NP = 36cm\). Biết chiều cao tương ứng với đáy \(NP\) là \(MH = 24cm\). Vậy chiều cao tương ứng với đáy \(MP\) là \(NK = \) \(cm\). Đáp án
Cho tam giác \(MNP\) có \(MP = 32cm,\,NP = 36cm\). Biết chiều cao tương ứng với đáy \(NP\) là \(MH = 24cm\). Vậy chiều cao tương ứng với đáy \(MP\) là \(NK = \) \(cm\). Phương pháp giải :
- Tính diện tích tam giác \(MNP\) theo công thức \(S = NP \times MH:2\). - Tính chiều cao \(NK\) theo công thức: \(NK = S \times 2:MP\). Lời giải chi tiết :
Theo đề bài ta có hình vẽ:
Diện tích tam giác \(MNP\) là: \(36 \times 24:2 = 432\;(c{m^2})\) Độ dài chiều cao \(NK\) là: \(432 \times 2:32 = 27\;(cm)\) Đáp số: \(27cm\). Vậy đáp án đúng điền vào ô trống là \(27\). Chú ý
Học sinh cần vẽ hình để xác định chiều cao và đáy tương ứng với nó.
Câu 14 :
A. \(569,5d{m^2}\) B. \(1139d{m^2}\) C. \(1394d{m^2}\) D. \(2278d{m^2}\) Đáp án
B. \(1139d{m^2}\) Phương pháp giải :
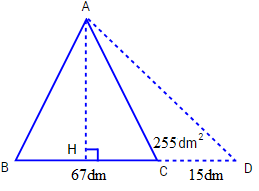
- Vẽ hình theo đề bài ta thấy diện tích phần tăng thêm là diện tích tam giác \(ACD\) có đáy \(CD = 15cm\) và chiều cao chính là chiều cao \(AH\) của tam giác \(ABC\), từ đó áp dụng công thức \(h = S \times 2:a\) ta tìm được chiều cao \(AH\). - Tính diện tích tam giác \(ABC\) theo công thức \(S = a \times h:2\). Lời giải chi tiết :
Theo bài ra ta có hình vẽ
Phần diện tích tăng thêm chính là diện tích của hình tam giác có đáy là $15dm$ và chiều cao cũng chính là chiều cao \(AH\) của tam giác \(ABC\). Chiều cao của tam giác \(ABC\) là: \(255 \times 2:15 = 34\;(dm)\) Diện tích tam giác \(ABC\) là \(67 \times 34:2 = 1139\left( {d{m^2}} \right)\) Đáp số: \(1139d{m^2}\). Chú ý
Với những dạng bài này, học sinh cần vẽ hình để xác định được được phần tăng thêm cũng như xác định chiều cao tương ứng với các cạnh của tam giác.
|














 Trong một tam giác có:
Trong một tam giác có: Nối câu mô tả hình dạng với hình tam giác tương ứng:
Nối câu mô tả hình dạng với hình tam giác tương ứng: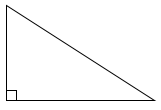


 Độ dài cạnh đáy của hình tam giác có chiều cao \(24cm\) và diện tích là \(420c{m^2}\) là:
Độ dài cạnh đáy của hình tam giác có chiều cao \(24cm\) và diện tích là \(420c{m^2}\) là:  Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống: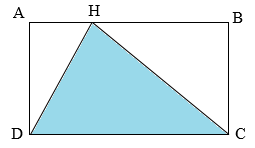
 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống: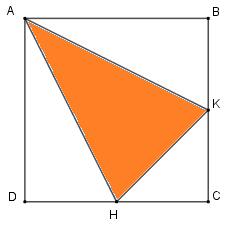

 Điền số thích hợp vào ô trống:
Điền số thích hợp vào ô trống: Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).
Cho tam giác \(ABC\) có $BC = 67dm$. Nếu kéo dài đoạn \(BC\) thêm một đoạn \(CD = 15dm\) thì diện tích tam giác tăng thêm $255d{m^2}$ . Tính diện tích tam giác \(ABC\).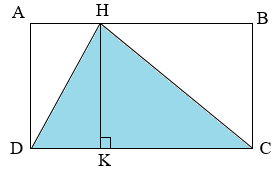





Danh sách bình luận