Toán lớp 5 trang 148, 149 Ôn tập về phân sốa) Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây: b) Viết hỗn số chỉ phần đã tô màu của mỗi hình dưới đây: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
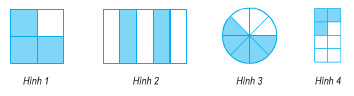
Bài 1 Video hướng dẫn giải a) Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây:
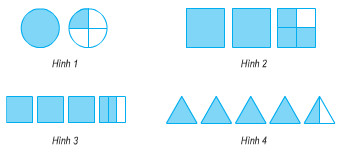
b) Viết hỗn số chỉ phần đã tô màu của mỗi hình dưới đây:
Phương pháp giải: Quan sát hình vẽ để viết phân số hoặc hỗn số tương ứng của mỗi hình. Lời giải chi tiết: a) Hình 1 : \( \displaystyle{3 \over 4}\) Hình 2 : \( \displaystyle{2 \over 5}\) Hình 3 : \( \displaystyle{5 \over 8}\) Hình 4 : \( \displaystyle{3 \over 8}\) b) Hình 1 : \( \displaystyle1{1 \over 4}\) Hình 2 : \( \displaystyle2{3 \over 4}\) Hình 3 : \( \displaystyle3{2 \over 3}\) Hình 4 : \( \displaystyle4{1 \over 2}\)
Bài 2 Video hướng dẫn giải Rút gọn các phân số: \(\dfrac{3}{6}\); \(\dfrac{18}{24}\); \(\dfrac{5}{35}\); \(\dfrac{40}{90}\); \(\dfrac{75}{30}\). Phương pháp giải: Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1. - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết: \(\dfrac{3}{6}= \dfrac{3:3}{6:3}= \dfrac{1}{2}\); \(\dfrac{18}{24} = \dfrac{18:6}{24:6} = \dfrac{3}{4}\); \(\dfrac{5}{35}= \dfrac{5:5}{35:5} = \dfrac{1}{7}\); \(\dfrac{40}{90} = \dfrac{40:10}{90:10}= \dfrac{4}{9}\); \(\dfrac{75}{30} = \dfrac{75:15}{30:15} = \dfrac{5}{2}\). Bài 3 Video hướng dẫn giải Quy đồng mẫu số các phân số: a) \(\dfrac{3}{4}\) và \(\dfrac{2}{5}\); b) \(\dfrac{5}{12}\) và \(\dfrac{11}{36}\); c) \(\dfrac{2}{3}\), \(\dfrac{3}{4}\) và \(\dfrac{4}{5}\). Phương pháp giải: Khi quy đồng mẫu số hai phân số có thể làm như sau: - Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai. - Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất. Lời giải chi tiết: a) \(\dfrac{3}{4}=\dfrac{3 \times 5}{4 \times 5}= \dfrac{15}{20}\); \(\dfrac{2}{5}=\dfrac{2 \times 4}{5 \times 4}=\dfrac{8}{20}\); b) \(\dfrac{5}{12}=\dfrac{5 \times 3}{12 \times 3}=\dfrac{15}{36}\); Giữ nguyên phân số \(\dfrac{11}{36}.\) c) \(\dfrac{2}{3}=\dfrac{2 \times 4 \times 5}{3 \times 4 \times5}=\dfrac{40}{60}\); \(\dfrac{3}{4}=\dfrac{3 \times 3 \times 5}{4 \times 3 \times 5}=\dfrac{45}{60}\); \(\dfrac{4}{5}=\dfrac{4 \times 3 \times 4}{5 \times 3 \times 4}=\dfrac{48}{60}\). Bài 4 Video hướng dẫn giải Điền dấu thích hợp \((>;\; <;\;=)\) vào chỗ chấm: \(\dfrac{7}{12}....\dfrac{5}{12}\) \(\dfrac{2}{5}.....\dfrac{6}{15}\) \(\dfrac{7}{10}....\dfrac{7}{9}\). Phương pháp giải: Áp dụng các quy tắc so sánh phân số: - Nếu hai phân số có cùng mẫu số, phân số nào có tử số lớn hơn thì phân số đó lớn hơn và ngược lại. - Nếu hai phân số có cùng tử số, phân số nào có mẫu số lớn hơn thì phân số đó bé hơn và ngược lại. - Nếu hai phân số không cùng mẫu số, ta có thể quy đồng mẫu số rồi so sánh hai phân số sau khi quy đồng. Lời giải chi tiết: +) \(\dfrac{7}{12} > \dfrac{5}{12}\) (vì \(7>5\)). +) Ta có: \(\dfrac{2}{5}= \dfrac{2 \times 3}{5 \times 3} = \dfrac{6}{15}\) Vậy \(\dfrac{2}{5} = \dfrac{6}{15}\). +) \(\dfrac{7}{10} < \dfrac{7}{9}\) (vì \(10>9\)). Bài 5 Video hướng dẫn giải Viết phân số thích hợp vào vạch giữa \( \dfrac {1}{3}\) và \( \dfrac {2}{3}\) trên tia số:
Phương pháp giải: Quy đồng hai phân số \( \dfrac {1}{3}\) và \( \dfrac {2}{3}\) với mẫu số chung là \(6\) rồi tìm phân số ở giữa hai phân số đó. Lời giải chi tiết: Ta có: \( \dfrac {1}{3} = \dfrac {2}{6}\) ; \( \dfrac {2}{3} = \dfrac {4}{6}\). Mà: \( \dfrac {2}{6} < \dfrac{3}{6}< \dfrac {4}{6}\) Ta điền như sau:
|















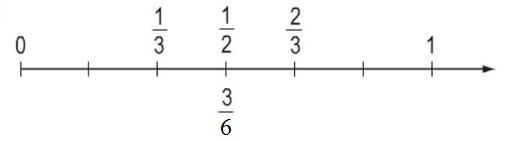






Danh sách bình luận