Toán lớp 5 trang 38, 39 Luyện tậpa) Chuyển các phân số thập phân sau đây thành hỗn số (theo mẫu): b) Chuyển các hỗn số của phần a) thành số thập phân (theo mẫu): Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Bài 1 Video hướng dẫn giải a) Chuyển các phân số thập phân sau đây thành hỗn số (theo mẫu): \(\dfrac{162}{10}\) \(\dfrac{734}{10}\) \(\dfrac{5608}{100}\) \(\dfrac{605}{100}\) Mẫu: \(\dfrac{162}{10} = 16\dfrac{2}{10}\) Cách làm:
Thương tìm được là số nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia. b) Chuyển các hỗn số của phần a) thành số thập phân (theo mẫu): Mẫu: \(16\dfrac{2}{10} = 16,2\) Phương pháp giải: - Lẩy tử số chia cho mẫu số. - Thương tìm được là phần nguyên; viết phần nguyên kèm theo một phân số có tử số là số dư, mẫu số là số chia. Lời giải chi tiết: a) Ta có:
Vậy: \(\dfrac{734}{10} = 73\dfrac{4}{10}\) \(\dfrac{5608}{100} = 56\dfrac{8}{100}\) \(\dfrac{605}{100} = 6\dfrac{5}{100}\) b) \(73\dfrac{4}{10}= 73,4\) \(56\dfrac{8}{100}= 56,08\) \(6\dfrac{5}{100} = 6,05\) Bài 2 Video hướng dẫn giải Chuyển các phân số thập phân sau thành số thập phân, rồi đọc các số thập phân đó: \(\dfrac{45}{10}\); \(\dfrac{834}{10}\); \(\dfrac{1954}{100}\); \(\dfrac{2167}{1000}\); \(\dfrac{2020}{10000}\). Phương pháp giải: Chuyển phân số thập phân đã cho dưới dạng hỗn số rồi viết thành số thập phân. Lời giải chi tiết: \(\dfrac{45}{10}= 4\dfrac{5}{10}= 4,5;\quad 4,5\) đọc là bốn phẩy năm. \(\dfrac{834}{10}= 83\dfrac{4}{10}= 83,4 ;\quad 83,4\) đọc là tám mươi ba phẩy bốn. \(\dfrac{1954}{100}= 19\dfrac{54}{100}= 19,54 ;\quad19,54\) đọc là mười chín phẩy năm mươi tư. \(\dfrac{2167}{1000}= 2\dfrac{167}{1000}= 2,167 ;\quad2,167\) đọc là hai phẩy một trăm sáu mươi bảy. \(\dfrac{2020}{10000}= 0,2020;\quad 0,2020\) đọc là không phẩy hai nghìn không trăm hai mươi. Bài 3 Video hướng dẫn giải Viết số thích hợp vào chỗ chấm (theo mẫu): \(2,1m = ....dm\) \(5,27m =.... cm\) \(8,3m = ...cm\) \(3,15m = ...cm\) Mẫu: \(2,1m=21dm\) Cách làm: \(\displaystyle 2,1m = 2{1 \over {10}}m = 2m\,\,1dm = 21dm\). Phương pháp giải: Quan sát ví dụ mẫu và làm tương tự với các câu còn lại. Lời giải chi tiết: \( \displaystyle 8,3m = 8\,{3 \over {10}}\,m =8\,{30 \over {100}}m \) \(= 8m\;30cm =830cm\) \( \displaystyle 5,27m = 5\,{{27} \over {100}}\,m = 5m\;27cm \) \(= 527cm\) \( \displaystyle 3,15m = 3\,{{15} \over {100}}\,m = 3m\;15cm \) \(= 315cm\). Bài 4 Video hướng dẫn giải a) Viết phân số \(\dfrac{3}{5}\) dưới dạng phân số thập phân có mẫu số là \(10\) và có mẫu số là \(100\). b) Viết hai phân số thập phân mới tìm được thành hai số thập phân. c) Có thể viết \(\dfrac{3}{5}\) thành những số thập phân nào? Phương pháp giải: Nhân cả tử số và mẫu số của phân số \(\dfrac{3}{5}\) với một số thích hợp để được phân số thập phân có mẫu số là \(10\) và có mẫu số là \(100\). Lời giải chi tiết: a) \(\dfrac{3}{5}=\dfrac{3 \times 2}{5\times 2}= \dfrac{6}{10}\) \(\dfrac{3}{5} = \dfrac{3 \times 20}{5\times 20}= \dfrac{60}{100}\) b) \(\dfrac{6}{10}= 0,6\) ; \(\dfrac{60}{100}= 0,60\) c) \(\dfrac{3}{5} = 0,6 = 0,60 = 0,600\) \(= 0,6000=...\)
|














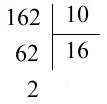







Danh sách bình luận