Trắc nghiệm Bài tập ôn tập chương 8 Toán 8Đề bài
Câu 1 :
Hình lăng trụ đứng tam giác có
Câu 2 :
Quan sát các hình vẽ dưới đây và cho biết hình nào là hình chóp lục giác?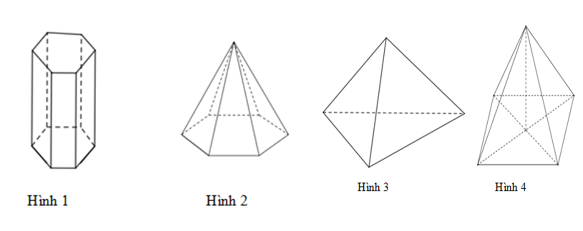 
Câu 3 :
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\), với mặt đáy $ABCD$ là hình chữ nhật. Khi đó:
Câu 4 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Điểm \(M\) thuộc đoạn thẳng $BD.$ Khi đó:
Câu 5 :
Hình chóp có $8$ cạnh thì đáy là hình gì?
Câu 6 :
Thể tích của hình lập phương trong hình là: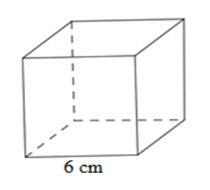 
Câu 7 :
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB = 8{\rm{ }}cm,$ đường cao $SO = 10{\rm{ }}cm.$ Hỏi thể tích của hình chóp đều là bao nhiêu?
Câu 8 :
Tính diện tích xung quanh của một hình lăng trụ đứng có đáy là hình ngũ giác đều cạnh 8 cm, biết rằng chiều cao của hình lăng trụ đứng là 5 cm.
Câu 9 :
Tính diện tích toàn phần hình chóp tứ giác đều dưới đây: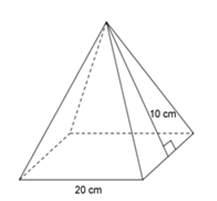 
Câu 10 :
Cho lăng trụ tam giác dưới đây. Tính thể tích hình lăng trụ đó?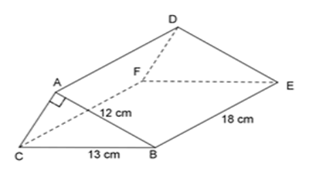 
Câu 11 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(A'C = \sqrt 3 \) . Tính thể tích của hình lập phương.
Câu 12 :
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\) có đáy là hình thang vuông ABCD vuông tại A, B \(\left( {A{\rm{D//}}BC} \right)\) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao ${\rm{AA}}' = 6\;cm$. Thể tích của hình lăng trụ là:
Câu 13 :
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, $M$ là trung điểm của $BC,$ ${\rm{AA}}' = AM = a$. Thể tích của lăng trụ bằng:
Câu 14 :
Hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh $a$ và diện tích hình chữ nhật \(A{\rm{D}}C'B'\) bằng \(2{{\rm{a}}^2}\), diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
Câu 15 :
Tính thể tích của hình chóp tứ giác đều có chiều cao là $4cm$ và độ dài cạnh đáy là $3cm.$
Câu 16 :
Tính diện tích xung quanh của hình hộp chữ nhật có bình phương độ dài đường chéo chính là $77$ ; kích thước đáy là $4$ và $6.$
Câu 17 :
Cho hình lăng trụ đứng đáy là hình thoi có hai đường chéo lần lượt là $8cm$ và $10cm.$ Tính chiều cao của lăng trụ đứng biết thể tích của lăng trụ đứng là $360c{m^3}$ .
Câu 18 :
Cho hình chóp tứ giác đều có cạnh đáy dài $16cm$ và trung đoạn dài $20cm.$ Tính thể tích hình chóp. (làm tròn đến hàng phần trăm)
Câu 19 :
Cho hình chóp tam giác đều $S.ABC$ có tất cả các cạnh bằng $2{\rm{ }}dm.$ Tính độ dài đoạn thẳng $MN$ nối trung điểm 2 cạnh đối $AB$ và $SC.$
Câu 20 :
Cho hình chóp cụt đều có 2 đáy là các hình vuông cạnh a và 2a, trung đoạn bằng a. Tính diện tích xung quanh của hình chóp cụt đều?
Câu 21 :
Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$ Câu 21.1
Tính bình phương đường cao $SH$ của hình chóp.
Câu 21.2
Tính diện tích xung quanh hình chóp
Câu 22 :
Cho hình hộp chữ nhật $ABCD.EFGH.$ Chọn câu đúng:
Câu 23 :
Cho hình hộp chữ nhật $ABCD.A'B'C'D' .$ Tính diện tích hình chữ nhật $ADC'B' \;$ biết $AB = 28cm,B' {D^2} = 3709,DD' = 45cm.$
Lời giải và đáp án
Câu 1 :
Hình lăng trụ đứng tam giác có
Đáp án : A Phương pháp giải :
Sử dụng kiến thức về hình lăng trụ đứng tam giác hoặc vẽ hình rồi đếm số mặt, số đỉnh, số cạnh. Lời giải chi tiết :
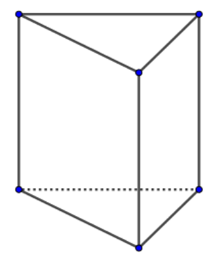 Quan sát hình vẽ ta thấy hình lăng trụ đứng tam giác có \(5\) mặt, \(6\) đỉnh và \(9\) cạnh.
Câu 2 :
Quan sát các hình vẽ dưới đây và cho biết hình nào là hình chóp lục giác?
Đáp án : B Phương pháp giải :
+ Vận dụng kiến thức lý thuyết về hình chóp và hình lăng trụ để tìm đáp án đúng. + Để ý rằng: "Hình chóp lục giác là hình chóp có đáy là hình lục giác". Lời giải chi tiết :
Hình 1 là hình lăng trụ có hai đáy là hai lục giác đều, hình 3 là hình chóp tam giác, hình 4 là hình chóp tứ giác. Hình 2 là hình chóp lục giác vì có đáy là hình lục giác và các cạnh bên giao nhau tại một điểm.
Câu 3 :
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\), với mặt đáy $ABCD$ là hình chữ nhật. Khi đó:
Đáp án : D Phương pháp giải :
- Áp dụng kiến thức về hình lăng trụ đứng và quan hệ giữa đường thẳng trong không gian - Áp dụng tính chất hình chữ nhật Lời giải chi tiết :
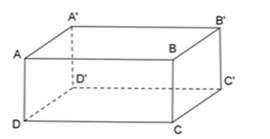 Vì $ABCD.A'B'C'D'$ là hình lăng trụ đứng có đáy là hình chữ nhật nên suy ra \(ABC{\rm{D}}.A'B'C'D'\) là hình hộp chữ nhật $ \Rightarrow {\rm{AA}}' = CC'$ (cùng bằng $BB'$)
Câu 4 :
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Điểm \(M\) thuộc đoạn thẳng $BD.$ Khi đó:
Đáp án : D Phương pháp giải :
- Vận dụng lý thuyết về hình lăng trụ đứng, quan hệ gữa điểm và mặt phẳng, đồng thời quan sát hình vẽ để làm bài Lời giải chi tiết :
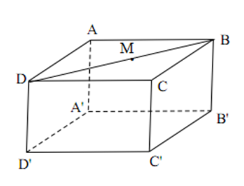 Vì \(M \in BD\) mà $BD \subset (ABCD)$ nên \(M \) thuộc mặt phẳng $\left( {ABCD} \right)$.
Câu 5 :
Hình chóp có $8$ cạnh thì đáy là hình gì?
Đáp án : B Phương pháp giải :
+ Sử dụng công thức liên hệ giữa số cạnh của hình chóp và số cạnh ở đáy của hình chóp: "Hình chóp có số cạnh gấp đôi số cạnh của đa giác ở đáy" Lời giải chi tiết :
Vì hình chóp có số cạnh gấp đôi số cạnh của đa giác ở đáy nên hình chóp có \(8\) cạnh thì đa giác đáy có \(8:2 = 4\) cạnh. Hay đáy là tứ giác.
Câu 6 :
Thể tích của hình lập phương trong hình là:
Đáp án : A Phương pháp giải :
- Vận dụng công thức tính thể tích hình lập phương cạnh $a$ là $V=a^3$. Lời giải chi tiết :
Thể tích hình lập phương \(V = {6^3} = 216\;c{m^3}\)
Câu 7 :
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB = 8{\rm{ }}cm,$ đường cao $SO = 10{\rm{ }}cm.$ Hỏi thể tích của hình chóp đều là bao nhiêu?
Đáp án : B Phương pháp giải :
- Vận dụng công thức tính thể tích hình chóp đều: \(V = \dfrac{1}{3}{S_đ}.h.\) Lời giải chi tiết :
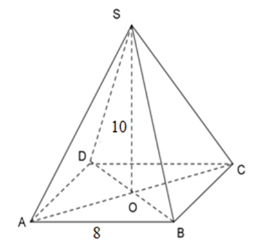 Tứ giác $ABCD$ là hình vuông cạnh $8cm$. Nên thể tích hình chóp tứ giác đều $S.ABCD$ là \( \Rightarrow V = \dfrac{1}{3}.{S_{ABCD}}.SO\)\( = \dfrac{1}{3}{.8^2}.10 = \dfrac{{640}}{3}\;c{m^3}.\)
Câu 8 :
Tính diện tích xung quanh của một hình lăng trụ đứng có đáy là hình ngũ giác đều cạnh 8 cm, biết rằng chiều cao của hình lăng trụ đứng là 5 cm.
Đáp án : D Phương pháp giải :
- Vận dụng công thức tính diện tích xung quanh của hình lăng trụ đứng: \({S_{xq}} = 2ph\) với p là nửa chu vi đáy và h là chiều cao của hình lăng trụ. Hay diện tích xung quanh của hình lăng trụ đứng bằng tích chu vi đáy với chiều cao lăng trụ. Lời giải chi tiết :
Chu vi đáy của hình lăng trụ đứng là $8.5$ (cm) Diện tích xung quanh là \({S_{xq}} = 8.5.5 = 200\;c{m^2}\)
Câu 9 :
Tính diện tích toàn phần hình chóp tứ giác đều dưới đây:
Đáp án : C Phương pháp giải :
- Vận dụng công thức tính diện tích toàn phần của hình chóp đều. \({S_{tp}} = {S_{xq}} + {S_đ}.\) Lời giải chi tiết :
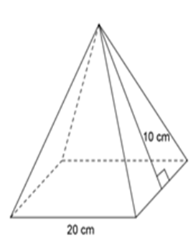 Mỗi mặt bên của hình chóp là tam giác có chiều cao 10 cm và cạnh đáy 20 cm. Diện tích một mặt bên của hình chóp là $\dfrac{1}{2}.10.20=100\, (cm^2)$ Diện tích xung quanh hình chóp là $S_{xq}=4.100=400\, (cm^2)$ $S_{tp} = S_{xq} + S_{đáy} =$ \(400 + 20.20 = 800\;c{m^2}\)
Câu 10 :
Cho lăng trụ tam giác dưới đây. Tính thể tích hình lăng trụ đó?
Đáp án : A Phương pháp giải :
- Vận dụng định lý Pitago kết hợp cách tính thể tích hình lăng trụ đứng: $V=S_đ.h$ để giải bài toán. Lời giải chi tiết :
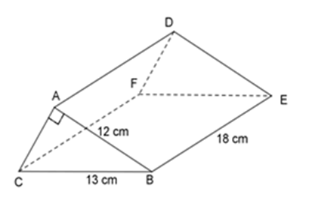 Kí hiệu như hình vẽ. Áp dụng định lý Pitago vào tam giác $ABC$ vuông tại $A.$ \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow A{C^2} = B{C^2} - A{B^2} = {13^2} - {12^2} = 25\\ \Rightarrow AC = 5\;cm\end{array}\) Vậy thể tích của hình lăng trụ đã cho là: \(V = {S_đ}.h\) \( = \dfrac{1}{2}AC.AB.BE = \dfrac{1}{2}.5.12.18 = 540\;c{m^2}\)
Câu 11 :
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(A'C = \sqrt 3 \) . Tính thể tích của hình lập phương.
Đáp án : B Phương pháp giải :
Sử dụng đường chéo hình lập phương cạnh \(a\) có độ dài \(a\sqrt 3 .\) Sử dụng công thức tính thể tích hình lập phương bằng lập phương độ dài một cạnh. Lời giải chi tiết :
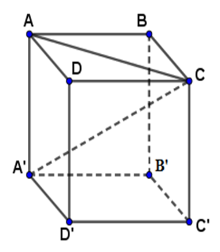 Xét hình lập phương \(ABCD.A'B'C'D'\) có \(A'C = AA'.\sqrt 3 = a\sqrt 3 \Rightarrow AA' = a\) Vậy thể tích hình lập phương là \(V = {a^3}\) .
Câu 12 :
Cho hình lăng trụ đứng \(ABC{\rm{D}}.A'B'C'D'\) có đáy là hình thang vuông ABCD vuông tại A, B \(\left( {A{\rm{D//}}BC} \right)\) và BC = 12 cm, AD = 16 cm, CD = 5 cm, đường cao ${\rm{AA}}' = 6\;cm$. Thể tích của hình lăng trụ là:
Đáp án : C Phương pháp giải :
- Kẻ $CH \bot AD$ tại H, áp dụng định lý Pytago - Áp dụng công thức tính thể tích hình lăng trụ đứng: $V = {S_đ}.h.$ Lời giải chi tiết :
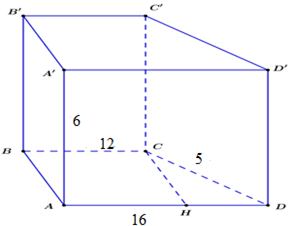 Trong mp $\left( {ABCD} \right)$ kẻ $CH$ vuông góc với $AD$ tại $H.$ Khi đó ta có $ABCH$ là hình chữ nhật. \(\left( {do\;\;\widehat A = \widehat B = \widehat H = 90^\circ } \right)\) \( \Rightarrow BC = AH = 12\;cm \)\(\Rightarrow H{\rm{D}} = A{\rm{D}} - AH = 16 - 12 = 4\;cm\) Xét tam giác $HCD$ vuông tại $H$ ta có: \(H{C^2} + H{{\rm{D}}^2} = C{{\rm{D}}^2} \Leftrightarrow H{C^2} = C{{\rm{D}}^2} - H{{\rm{D}}^2} = {5^2} - {4^2} = 25 - 16 = 9 \Rightarrow HC = 3\;cm\) Vậy thể tích của hình lăng trụ là: $V{\rm{ }} = {\rm{ }}{S_{ABCD}}.h{\rm{ }} = {\rm{ }}{S_{ABCD}}.AA'$ \( = \dfrac{1}{2}AA'.\left( {BC + AD} \right).CH = \dfrac{1}{2}.3.(12 + 16).6 = 252\;c{m^3}\) \(\)
Câu 13 :
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều, $M$ là trung điểm của $BC,$ ${\rm{AA}}' = AM = a$. Thể tích của lăng trụ bằng:
Đáp án : B Phương pháp giải :
- Áp dụng định lý Pytago và công thức tính thể tích hình lăng trụ đứng. Lời giải chi tiết :
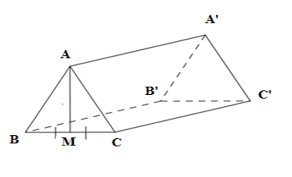 Vì tam giác $ABC$ là tam giác đều nên $AM$ vừa là trung tuyến vừa là đường cao của tam giác $ABC.$ Gọi chiều dài của cạnh tam giác $ABC$ là $x.\,\,\left( {x > 0} \right)$ \( \Rightarrow BM = MC = \dfrac{x}{2},\;AB = AC = BC = x\) Xét tam giác vuông $MAC,$ ta có: \(A{M^2} + M{C^2} = A{C^2} \Leftrightarrow {a^2} + \dfrac{{{x^2}}}{4} = {x^2} \Leftrightarrow \dfrac{{3{{\rm{x}}^2}}}{4} = {a^2} \Rightarrow x = \dfrac{{2\sqrt 3 }}{3}a\) Vậy thể tích của hình lăng trụ là: $V{\rm{ }} = {\rm{ }}{S_{ABC}}.h{\rm{ }} $ \(=\dfrac{1}{2}.AM.BC.AA' = \dfrac{1}{2}a.\dfrac{{2\sqrt 3 }}{3}a.a = \dfrac{{{a^3}\sqrt 3 }}{3}\)
Câu 14 :
Hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh $a$ và diện tích hình chữ nhật \(A{\rm{D}}C'B'\) bằng \(2{{\rm{a}}^2}\), diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
Đáp án : A Phương pháp giải :
- Áp dụng công thức tính diện tích xung quanh hình hộp chữ nhật \({S_{xq}} = 2ph\) (với p là nửa chu vi đáy) và công thức tính diện tích hình chữ nhật, định lý Pytago Lời giải chi tiết :
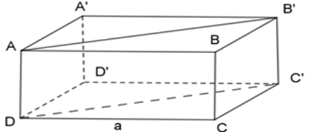 Ta có \(A{\rm{D}}C'B'\) là hình chữ nhật. \( \Rightarrow {S_{A{\rm{D}}C'B'}} = A{\rm{D}}.DC' = 2{{\rm{a}}^2} \Rightarrow a.DC' = 2{{\rm{a}}^2} \Rightarrow DC' = 2{\rm{a}}\) Xét tam giác vuông \(CC'D\) ta có: \(CC{'^2} + C{{\rm{D}}^2} = C'{D^2} \Leftrightarrow CC{'^2} + {a^2} = {(2{\rm{a}})^2} \Leftrightarrow CC{'^2} = 4{{\rm{a}}^2} - {a^2} = 3{{\rm{a}}^2} \Rightarrow CC' = a\sqrt 3 \) Vậy diện tích xung quanh của hình hộp chữ nhật là: Sxq \( = 2.p.CC' = 2.\dfrac{{4{\rm{a}}}}{2}.a\sqrt 3 = 4{{\rm{a}}^2}\sqrt 3 \)
Câu 15 :
Tính thể tích của hình chóp tứ giác đều có chiều cao là $4cm$ và độ dài cạnh đáy là $3cm.$
Đáp án : A Phương pháp giải :
Sử dụng công thức tính thể tích hình chóp đều \(V = \dfrac{1}{3}S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao. Lời giải chi tiết :
Hình chóp tứ giác đều thì có đáy là hình vuông.
Câu 16 :
Tính diện tích xung quanh của hình hộp chữ nhật có bình phương độ dài đường chéo chính là $77$ ; kích thước đáy là $4$ và $6.$
Đáp án : D Phương pháp giải :
Nếu hình hộp chữ nhật có ba kích thước là \(a;b;c\) thì có độ dài đường chéo chính là $\sqrt {{a^2} + {b^2} + {c^2}} $ Sử dụng công thức tính diện tích xung quanh hình hộp chữ nhật bằng chu vi đáy nhân chiều cao. Lời giải chi tiết :
Gọi độ dài đường cao hình hộp chữ nhật là \(h\,\,\left( {h > 0} \right)\) Vậy diện tích xung quanh của hình hộp chữ nhật là:
Câu 17 :
Cho hình lăng trụ đứng đáy là hình thoi có hai đường chéo lần lượt là $8cm$ và $10cm.$ Tính chiều cao của lăng trụ đứng biết thể tích của lăng trụ đứng là $360c{m^3}$ .
Đáp án : C Phương pháp giải :
Sử dụng công thức tính diện tích hình thoi bằng nửa tích hai đường chéo Sử dụng công thức tính thể tích lăng trụ bằng tích diện tích đáy với chiều cao từ đó tính được chiều cao. Lời giải chi tiết :
Diện tích đáy hình thoi là: $\dfrac{1}{2}.8.10 = 40(c{m^2})$ Vì $V = {S_đ}.h \Rightarrow h = \dfrac{V}{{{S_đ}}}$ nên chiều cao của lăng trụ đứng là: $360:40 = 9(cm)$
Câu 18 :
Cho hình chóp tứ giác đều có cạnh đáy dài $16cm$ và trung đoạn dài $20cm.$ Tính thể tích hình chóp. (làm tròn đến hàng phần trăm)
Đáp án : A Phương pháp giải :
Tính chiều cao theo định lý Pytago Tính thể tích khối chóp \(V = \dfrac{1}{3}S.h\) Lời giải chi tiết :
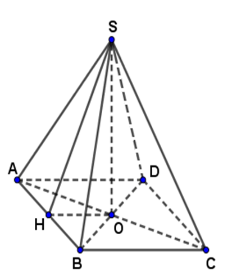 Xét hình chóp tứ giác đều $S.ABCD\;$ có đáy là hình vuông cạnh $16cm$. $O$ là giao điểm của hai đường chéo trong hình vuông $ABCD$ nên $O$ là trung điểm $AC$ Vậy thể tích hình chóp $S.ABCD\;$ là
Câu 19 :
Cho hình chóp tam giác đều $S.ABC$ có tất cả các cạnh bằng $2{\rm{ }}dm.$ Tính độ dài đoạn thẳng $MN$ nối trung điểm 2 cạnh đối $AB$ và $SC.$
Đáp án : A Phương pháp giải :
- Tính \(CM\) theo định lý Pytago - Tính \(MN\) theo định lý Pytago Lời giải chi tiết :
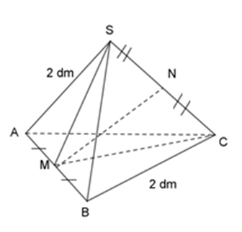 Theo đề bài ta có: \(\begin{array}{l}AM = MB = \dfrac{1}{2}AB = 1\;dm\\SN = NC = \dfrac{1}{2}SC = 1\;dm\end{array}\) Ta có $CM$ là đường trung tuyến của tam giác $ABC.$ Vì tam giác $ABC$ là tam giác đều nên $CM$ cũng là đường cao của tam giác $ABC.$ Áp dụng định lý Pitago vào tam giác $CMB$ vuông tại $M:$ \(\begin{array}{l}M{C^2} + M{B^2} = B{C^2}\\ \Leftrightarrow M{C^2} = B{C^2} - M{B^2} = {2^2} - 1 = 3\\ \Rightarrow MC = \sqrt 3 \;dm\end{array}\) Tương tự ta xét tam giác vuông $SMB,$ ta tính được: \(SM = \sqrt 3 \;dm\) Xét tam giác $SMC$ có: \(M{\rm{S}} = MC = \sqrt 3 \;dm\) \( \Rightarrow \) Tam giác $SMC$ là tam giác cân tại $M.$ \( \Rightarrow \) MN vừa là đường trung tuyến vừa là đường cao của tam giác SMC. Áp dụng định lý Pitago cho tam giác MNC vuông tại N: \(\begin{array}{l}M{N^2} + N{C^2} = M{C^2}\\ \Leftrightarrow M{N^2} = M{C^2} - N{C^2} = 3 - 1 = 2\\ \Rightarrow MN = \sqrt 2 \;dm\end{array}\)
Câu 20 :
Cho hình chóp cụt đều có 2 đáy là các hình vuông cạnh a và 2a, trung đoạn bằng a. Tính diện tích xung quanh của hình chóp cụt đều?
Đáp án : A Phương pháp giải :
- Diện tích xung quanh hình chóp cụt đều bằng tổng diện tích các mặt bên nên ta tính diện tích một mặt bên để suy ra diện tích xung quanh hình chóp cụt đều. Lời giải chi tiết :
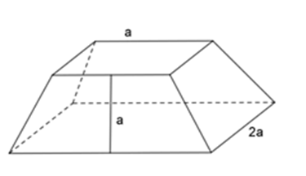 Hình chóp cụt đều có 4 mặt bên là các hình thang cân bằng nhau. Suy ra, diện tích xung quanh của hình chóp cụt đều là tổng diện tích 4 hình thang cân, khi đó diện tích một mặt bên là $S=\dfrac{(a+2a).a}{2}=\dfrac{3a^2}{2}$ Diện tích xung quanh hình chóp cụt đều là \({S_{xq}} = 4. \dfrac{3a^2}{2}= 6{{\rm{a}}^2}\)
Câu 21 :
Cho hình chóp tứ giác đều $S.ABCD$ , đáy $ABCD$ là hình vuông có cạnh $3{\rm{ }}cm,$ cạnh bên $SB$ bằng $5{\rm{ }}cm.$ Câu 21.1
Tính bình phương đường cao $SH$ của hình chóp.
Đáp án : A Phương pháp giải :
+ Lấy $H$ là giao của 2 đường chéo hình vuông $AC$ và $BD,$ khi đó ta có $SH$ là đường cao của hình chóp đều. + Vận dụng định lý Pitago, tính chất đường cao, đường trung tuyến, tam giác đều, tam giác cân để tính chiều cao. Lời giải chi tiết :
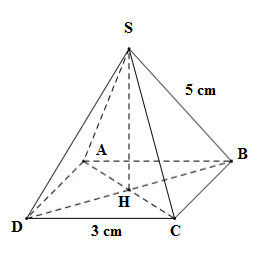 Lấy H là giao của 2 đường chéo hình vuông $AC$ và $BD,$ khi đó ta có $SH$ là đường cao của hình chóp đều. +) Áp dụng định lý Pitago cho tam giác $ABC$ vuông tại $B:$ \(\begin{array}{l}\;\;\;\;A{B^2} + B{C^2} = A{C^2}\\ \Leftrightarrow A{C^2} = {3^2} + {3^2} = 18\\ \Rightarrow AC = \sqrt {18} = 3\sqrt 2 \;cm\end{array}\) \( \Rightarrow HC = \dfrac{1}{2}AC = \dfrac{1}{2}.3\sqrt 2 = \dfrac{{3\sqrt 2 }}{2}\;cm\) (Vì H là trung điểm AC) Áp dụng định lý Pitago cho tam giác SHC vuông tại H có: \(\begin{array}{l}\;\;\;\;S{H^2} + H{C^2} = S{C^2}\\ \Leftrightarrow S{H^2} = S{C^2} - H{C^2} = {5^2} - {\left( {\dfrac{{3\sqrt 2 }}{2}} \right)^2} = \dfrac{{82}}{4} = \dfrac{{41}}{2}\end{array}\) Vậy \(S{H^2} = \dfrac{{41}}{2}.\) Câu 21.2
Tính diện tích xung quanh hình chóp
Đáp án : A Phương pháp giải :
+ Kẻ $SK$ vuông góc với $BC$ (\(K \in BC\)) + Sử dụng công thức tính diện tích xung quanh của hình chóp đều để làm bài. Lời giải chi tiết :
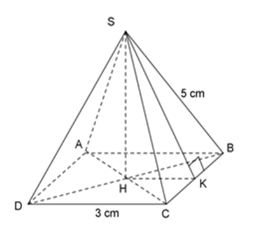 + Kẻ $SK$ vuông góc với $BC$ (\(K \in BC\)) + Vì tam giác $SBC$ là tam giác cân tại $S$ nên $SK$ vừa là đường cao vừa là đường trung tuyến. \( \Rightarrow CK = KB = \dfrac{1}{2}BC = \dfrac{3}{2}\;cm\) Áp dụng định lý Pitago cho tam giác $SKB$ vuông tại $K:$ \(\begin{array}{l}\;\;\;S{K^2} + K{B^2} = S{B^2}\\ \Leftrightarrow S{K^2} = S{B^2} - K{B^2} = {5^2} - {\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{91}}{4}\\ \Rightarrow SK = \dfrac{{\sqrt {91} }}{2}\;cm.\end{array}\) Vậy diện tích xung quanh của hình chóp đều $S.ABCD$ là: \({S_{xq}} =4.S_{SBC}= 4.\dfrac{1}{2}.BC.SK\)\(=4.\dfrac{1}{2}.3.\dfrac{{\sqrt {91} }}{2} = 3\sqrt {91} \;c{m^2}\)
Câu 22 :
Cho hình hộp chữ nhật $ABCD.EFGH.$ Chọn câu đúng:
Đáp án : D Phương pháp giải :
- Sử dụng quan hệ song song, vuông góc giữa các cạnh, các mặt trong hình hộp chữ nhật. - Sử dụng định lý Pytago Lời giải chi tiết :
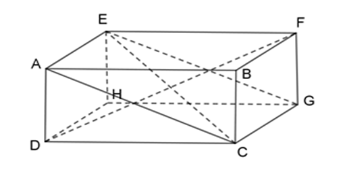 + ) Ta có:\(\) \(AE//CG,\;A{\rm{E}} = CG\;(gt)\) Suy ra tứ giác ACGE là hình bình hành. Mặt khác: \(A{\rm{E}} \bot mp(EFGH)\) Mà \(EG \subset mp(EFGH) \Rightarrow AE \bot EG\;\)tại $E.$ Vậy tứ giác $ACGE$ là hình chữ nhật nên $A$ đúng. +) Vì \(DH \bot mp(EFGH)\) nên \(DH \bot HF\) tại $H.$ Áp dụng định lý Pitago cho tam giác $DHF$ vuông tại $H,$ ta có: \(D{H^2} + H{F^2} = D{F^2}\;(1)\) Vì \(A{\rm{E}} \bot mp(ABC{\rm{D}})\) nên \(A{\rm{E}} \bot AC\) tại $A.$ Áp dụng định lý Pitago cho tam giác EAC vuông tại A, ta có: \(E{{\rm{A}}^2} + A{C^2} = E{C^2}\;(2)\) Mà DH = AE; HF = EG = AC (Hai đường chéo của hình chữ nhật) (3) Từ (1), (2), (3) suy ra: \(D{F^2} = E{C^2} \Rightarrow DF = CE\;\)nên B đúng.
Câu 23 :
Cho hình hộp chữ nhật $ABCD.A'B'C'D' .$ Tính diện tích hình chữ nhật $ADC'B' \;$ biết $AB = 28cm,B' {D^2} = 3709,DD' = 45cm.$
Đáp án : D Phương pháp giải :
Sử dụng định lý Pytago và mối quan hệ giữa các cạnh, các mặt trong hình hộp chữ nhật Lời giải chi tiết :
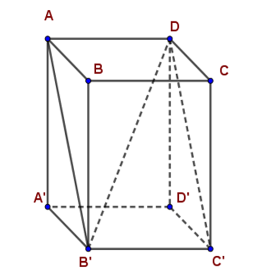 Xét tam giác $AA' B'$ vuông tại $A' $ có: $AA' = DD' = 45cm$ và $A' B' = AB = 28cm$ Áp dụng định lý Pytago ta có: Ta có: $AD \bot AA' ;AD \bot AB$ suy ra $AD \bot mp(AA' B' B) \Rightarrow AD \bot AB' $ Vậy diện tích $ADC' B' $ bằng $AD.AB' = 30.53 = 1590(c{m^2})$
|
