Trắc nghiệm Bài 7: Trường hợp đồng dạng thứ ba Toán 8Đề bài
Câu 1 :
Nếu 2 tam giác ABC và DEF có \(\widehat A = \widehat D\), \(\widehat C = \widehat F\) thì:
Câu 2 :
Cho hình bên biết $AB = 6\,cm,AC = 9\,cm$ , \(\widehat {ABD} = \widehat {BCA}\). Độ dài đoạn $AD$ là: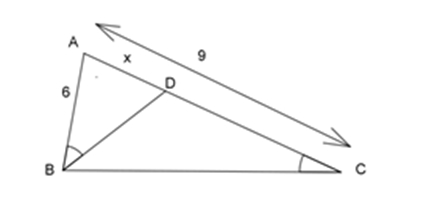 
Câu 3 :
Nếu 2 tam giác ABC và DEF có \(\widehat A = {70^0},\;\widehat C = {60^0},\;\widehat E = {50^0},\;\widehat F = {70^0}\) thì chứng minh được:
Câu 4 :
Tính giá trị của $x$ trong hình dưới đây: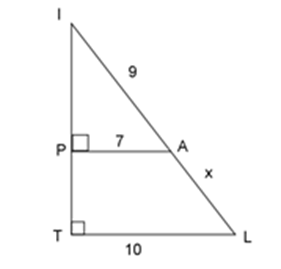 
Câu 5 :
Cho hình thang $ABCD$ (\(AB\,{\rm{//}}\,CD\)) có \(\widehat {ADB} = \widehat {BCD}\), $AB = 2cm$ , \(BD = \sqrt 5 \,cm\), ta có:
Cho tam giác $ABC$ cân tại $A$ . Trên cạnh $AC$ lấy điểm $M$ , trên đoạn thẳng $BM$ lấy điểm $K$ sao cho $\widehat {BCK} = \widehat {ABM}$ . Câu 6
Tam giác \(MBC\) đồng dạng với tam giác
Câu 7
Tích \(MB.MK\) bằng
Cho $\Delta ABC$ có các đường cao $BD$ và $CE$ cắt nhau tại $H.$ Gọi $M$ là giao của $AH$ với $BC.$ Câu 8
Chọn câu đúng.
Câu 9
Chọn khẳng định sai.
Câu 10 :
Cho hình bình hành $ABCD$ , điểm $F$ trên cạnh $BC$ . Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G$ . Chọn khẳng định sai.
Câu 11 :
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
Cho $\Delta ABC$ cân tại $A$ , có $BC = 2a$ , $M$ là trung điểm $BC$ , lấy $D,E$ thuộc $AB,AC$ sao cho \(\widehat {DME} = \widehat {ABC}\). Câu 12
Tích $BD.CE$ bằng
Câu 13
Góc \(BDM\) bằng với góc nào dưới đây?
Lời giải và đáp án
Câu 1 :
Nếu 2 tam giác ABC và DEF có \(\widehat A = \widehat D\), \(\widehat C = \widehat F\) thì:
Đáp án : A Phương pháp giải :
Từ dữ kiện đã có suy ra được $2$ tam giác đồng dạng theo trường hợp góc – góc Lời giải chi tiết :
Xét \(\Delta ABC\) và \(\Delta DEF\) có: \(\widehat A = \widehat D\)(gt) \(\widehat C = \widehat F\) (gt) \( \Rightarrow \Delta ABC\backsim\Delta DEF\;(g - g)\)
Câu 2 :
Cho hình bên biết $AB = 6\,cm,AC = 9\,cm$ , \(\widehat {ABD} = \widehat {BCA}\). Độ dài đoạn $AD$ là:
Đáp án : C Phương pháp giải :
Bước 1: Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp góc – góc. Bước 2: Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của x. Lời giải chi tiết :
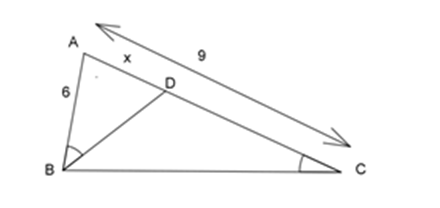 Xét \(\Delta ABD\) và \(\Delta ACB\) có: \(\widehat A\;chung\) \(\widehat {ABD} = \widehat {BCA}\;(gt)\) \( \Rightarrow \Delta ABD\backsim\Delta ACB\;(g - g)\) \( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}} \Leftrightarrow \dfrac{6}{9} = \dfrac{x}{6} \Leftrightarrow x = \dfrac{{6.6}}{9} = 4\;cm\)
Câu 3 :
Nếu 2 tam giác ABC và DEF có \(\widehat A = {70^0},\;\widehat C = {60^0},\;\widehat E = {50^0},\;\widehat F = {70^0}\) thì chứng minh được:
Đáp án : A Phương pháp giải :
Từ dữ kiện đã có suy ra các dữ kiện cần thiết để chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc. Lời giải chi tiết :
Xét \(\Delta ABC\) có: \(\begin{array}{l}\,\,\,\,\,\,\,\widehat A + \widehat B + \widehat C = {180^0}\\ \Leftrightarrow {70^0} + \widehat B + {60^0} = {180^0}\\ \Leftrightarrow \widehat B = {180^0} - {70^0} - {60^0} = {50^0}\end{array}\) Xét \(\Delta ABC\) và \(\Delta FED\) có: \(\widehat A = \widehat F = {70^0}\) \(\widehat B = \widehat E = {50^0}\) \( \Rightarrow \Delta ABC\backsim\Delta FED\;(g - g)\)
Câu 4 :
Tính giá trị của $x$ trong hình dưới đây:
Đáp án : B Phương pháp giải :
Bước 1: Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc. Bước 2: Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị $x$ . Lời giải chi tiết :
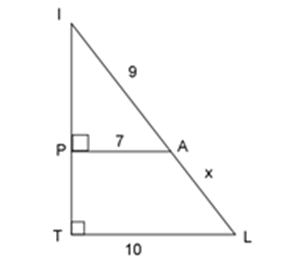 Xét \(\Delta IPA\) và \(\Delta ITL\) ta có: \(+) \widehat {IPA} = \widehat {ITL} = {90^0}\\ +) \widehat {TIL}\,\,\,chung\\ \Rightarrow \Delta IPA\backsim\Delta ITL\;(g - g)\\ \Rightarrow \dfrac{{PA}}{{TL}} = \dfrac{{IA}}{{IL}} \Leftrightarrow \dfrac{{PA}}{{TL}} = \dfrac{{IA}}{{IA + AL}} \Leftrightarrow \dfrac{7}{{10}} = \dfrac{9}{{9 + x}}\)\( \Leftrightarrow x = \dfrac{{27}}{7}\)
Câu 5 :
Cho hình thang $ABCD$ (\(AB\,{\rm{//}}\,CD\)) có \(\widehat {ADB} = \widehat {BCD}\), $AB = 2cm$ , \(BD = \sqrt 5 \,cm\), ta có:
Đáp án : D Phương pháp giải :
- Chứng minh $2$ tam giác đồng dạng theo trường hợp góc – góc. - Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra độ dài đoạn thẳng $CD$ . Lời giải chi tiết :
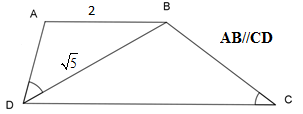 Vì \(AB\,{\rm{//}}\,CD\) nên: \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong) Xét \(\Delta ADB\) và \(\Delta BCD\) ta có: \(\widehat {ABD} = \widehat {BDC}\) (chứng minh trên) \(\widehat {ADB} = \widehat {BCD}\) (theo gt) \( \Rightarrow \Delta ADB\backsim\Delta BCD\;(g - g)\) \( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{DB}}{{CD}}\)\( \Leftrightarrow \dfrac{2}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{{CD}} \)\(\Leftrightarrow CD = \dfrac{{\sqrt 5 .\sqrt 5 }}{2} = \dfrac{5}{2} = 2,5\;cm\) Cho tam giác $ABC$ cân tại $A$ . Trên cạnh $AC$ lấy điểm $M$ , trên đoạn thẳng $BM$ lấy điểm $K$ sao cho $\widehat {BCK} = \widehat {ABM}$ . Câu 6
Tam giác \(MBC\) đồng dạng với tam giác
Đáp án : A Phương pháp giải :
- Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc. Lời giải chi tiết :
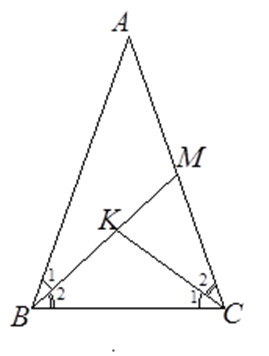 Tam giác $ABC$ cân tại $A$ nên $\widehat {ABC} = \widehat {ACB}$, ta lại có $\widehat {{B_1}} = \widehat {{C_1}}$ (gt) nên $\widehat {{B_2}} = \widehat {{C_2}}$ . $\Delta MBC$ và $\Delta MCK$có $\widehat {BMC}$ là góc chung; $\widehat {{B_2}} = \widehat {{C_2}}$ (chứng minh trên). Do đó $\Delta MBC\backsim\Delta MCK$ (g.g). Câu 7
Tích \(MB.MK\) bằng
Đáp án : C Phương pháp giải :
- Từ đó hai tam giác đồng dạng ta rút ra được tỉ lệ thức phù hợp. Lời giải chi tiết :
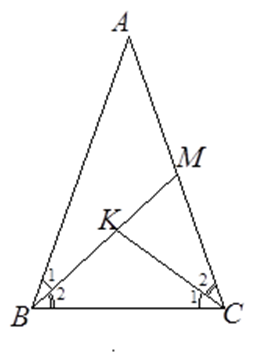 Vì $\Delta MBC\backsim\Delta MCK$ nên $\dfrac{{MC}}{{MK}} = \dfrac{{MB}}{{MC}}$ (hai cạnh tương ứng tỉ lệ) Suy ra $M{C^2} = MB.MK$. Cho $\Delta ABC$ có các đường cao $BD$ và $CE$ cắt nhau tại $H.$ Gọi $M$ là giao của $AH$ với $BC.$ Câu 8
Chọn câu đúng.
Đáp án : C Phương pháp giải :
Chứng minh hai tam giác đồng dạng theo trường hợp góc-góc. Lời giải chi tiết :
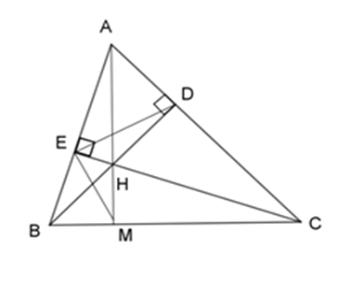 Xét \(\Delta HBE\) và \(\Delta HCD\) có: \(\widehat {BDC} = \widehat {CEB} = {90^0}\) \(\widehat {EHB} = \widehat {DHC}\) (2 góc đối đỉnh) \( \Rightarrow \Delta HBE\backsim\Delta HCD\)(g – g) Xét \(\Delta ABD\) và \(\Delta ACE\) có \(\widehat {AEC} = \widehat {BDA} = 90^\circ \) \(\widehat A\) chung Nên \(\Delta ABD\backsim\Delta ACE\,\left( {g - g} \right)\). Câu 9
Chọn khẳng định sai.
Đáp án : D Phương pháp giải :
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh yêu cầu của bài toán. Lời giải chi tiết :
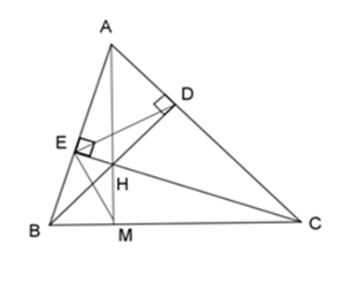 Theo cmt ta có: \(\Delta HBE\backsim\Delta HCD\) \( \Rightarrow \dfrac{{HE}}{{HD}} = \dfrac{{HB}}{{HC}} \Leftrightarrow \dfrac{{HE}}{{HB}} = \dfrac{{HD}}{{HC}}\) Xét \(\Delta HED\) và \(\Delta HBC\) ta có: \(\dfrac{{HE}}{{HB}} = \dfrac{{HD}}{{HC}}\) (chứng minh trên) \(\widehat {EHD} = \widehat {BHC}\) (2 góc đối đỉnh) \(\begin{array}{l}\widehat {HDE} = \widehat {HAE}\\ \Rightarrow \Delta HED\backsim\Delta HBC\,\,\,\left( {c - g - c} \right).\\ \Rightarrow \widehat {HDE} = \widehat {HCB}\,\,\,\,\,\left( 1 \right)\end{array}\) Mà đường cao BD và CE cắt nhau tại H (theo giả thiết) \( \Rightarrow \) H là trực tâm của \(\Delta ABC\). \( \Rightarrow AH \bot BC\) tại M \( \Rightarrow \widehat {AMB} = {90^0}\). Xét \(\Delta AMB\) và \(\Delta CEB\) có: \(\widehat {CEB} = \widehat {AMB} = {90^0}\) \(\widehat B\) chung \( \Rightarrow \Delta AMB\backsim\Delta CEB\;(g - g)\) \( \Rightarrow \widehat {MAB} = \widehat {ECB}\;hay\;\widehat {HAE} = \widehat {HCB}\;(2)\) Từ (1) và (2) ta có: \(\widehat {HDE} = \widehat {HAE}\) nên A, B, C đúng. D sai.
Câu 10 :
Cho hình bình hành $ABCD$ , điểm $F$ trên cạnh $BC$ . Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G$ . Chọn khẳng định sai.
Đáp án : C Phương pháp giải :
- Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc. Lời giải chi tiết :
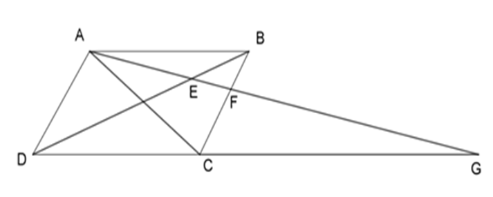 Có ABCD là hình bình hành nên: \(AD{\rm{//}}BC,\;AB{\rm{//}}\,DC\) \( \Rightarrow \widehat {ADE} = \widehat {FBE}\)(cặp góc so le trong) \( \Rightarrow \widehat {ABE} = \widehat {EDG}\)(cặp góc so le trong) Xét tam giác $BFE$ và tam giác $DAE$ có: \(\widehat {ADE} = \widehat {FBE}\;(cmt)\) \(\widehat {AED} = \widehat {FEB}\)(đối đỉnh) \( \Rightarrow \Delta BFE\backsim\Delta DAE\;(g - g)\)nên A đúng, C sai. Xét tam giác $DGE$ và tam giác $BAE$ có: \(\widehat {ABE} = \widehat {EDG\;}(cmt)\) \(\widehat {AEB} = \widehat {GED}\)(đối đỉnh) \( \Rightarrow \Delta DGE\backsim\Delta BAE\;(g - g)\)hay \(\Delta DEG\backsim\Delta BEA\) nên B, D đúng.
Câu 11 :
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
Đáp án : A Phương pháp giải :
Bước 1: Trên tia đối của tia $AC$ lấy điểm $D$ sao cho $AD = AB$ Bước 2: Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc. Bước 3: Từ tam giác đồng dạng suy ra tỉ lệ cạnh thích hợp để tính \(BC\) . Lời giải chi tiết :
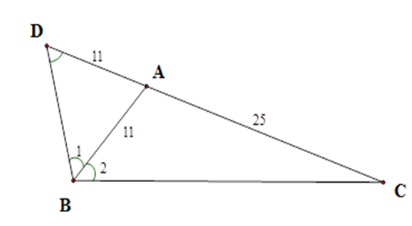 Trên tia đối của tia $AC$ lấy điểm $D$ sao cho $AD = AB$ . Tam giác $ABD$ cân tại $A$ nên \(\widehat {BAC} = \widehat {{B_1}} + \widehat D = 2\widehat D\) . Ta lại có $\widehat {BAC} = 2\widehat {{B_2}}$ nên \(\widehat D = \widehat {{B_2}}\) . Xét \(\Delta CBA\) và \(\Delta CDB\) có \(\widehat C\) chung và \(\widehat D = \widehat {{B_2}}\) Nên \(\Delta CBA\backsim\Delta CDB\,\left( {g - g} \right)\) nên \(\dfrac{{CB}}{{CD}} = \dfrac{{AC}}{{BC}}\) , tức là \(\dfrac{{CB}}{{36}} = \dfrac{{25}}{{BC}}\). Từ đó \(B{C^2} = 25.36\) suy ra \(BC = 5.6 = 30(cm)\). Cho $\Delta ABC$ cân tại $A$ , có $BC = 2a$ , $M$ là trung điểm $BC$ , lấy $D,E$ thuộc $AB,AC$ sao cho \(\widehat {DME} = \widehat {ABC}\). Câu 12
Tích $BD.CE$ bằng
Đáp án : C Phương pháp giải :
Chứng minh các cặp tam giác đồng dạng, từ đó rút ra dữ kiện cần thiết để chứng minh Lời giải chi tiết :
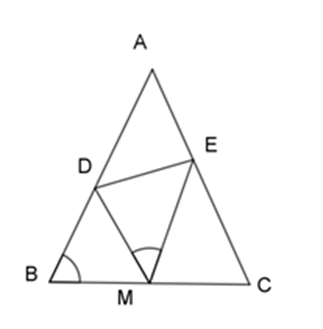 + Ta có: \(\widehat {DMC} = \widehat {DME} + \widehat {EMC}\) Mặt khác: \(\widehat {DMC} = \widehat {ABC} + \widehat {BDM}\) (góc ngoài tam giác) Mà: \(\widehat {DME} = \widehat {ABC}\)(gt) nên \(\widehat {BDM} = \widehat {EMC}\) + Ta có: \(\widehat {ABC} = \widehat {ACB}\) ($\Delta ABC$ cân tại $A$ ) và \(\widehat {BDM} = \widehat {EMC}\) (chứng minh trên) \( \Rightarrow \)\(\Delta BDM\backsim\Delta CME\;(g - g)\) \( \Rightarrow \dfrac{{BD}}{{CM}} = \dfrac{{BM}}{{CE}} \Rightarrow BD.CE = CM.BM\) Lại có M là trung điểm của BC và BC = 2a \( \Rightarrow \)BM = MC = a \( \Rightarrow BD.CE = {a^2}\) không đổi. Câu 13
Góc \(BDM\) bằng với góc nào dưới đây?
Đáp án : B Phương pháp giải :
Từ hai tam giác đồng dạng đã biết suy ra tỉ lệ cạnh thích hợp để chứng minh \(\Delta BDM\backsim\Delta MDE\;(c - g - c)\) để suy ra hai góc bằng nhau. Lời giải chi tiết :
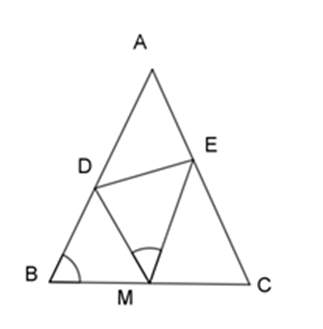 Ta có: \(\Delta BDM\backsim\Delta CME\;\) (chứng minh trên) \( \Rightarrow \dfrac{{DM}}{{ME}} = \dfrac{{BD}}{{CM}} = \dfrac{{BD}}{{BM}}\) (do CM = BM (gt)) \( \Rightarrow \dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}\) Xét \(\Delta BDM\) và \(\Delta MDE\) ta có: \(\dfrac{{BD}}{{DM}} = \dfrac{{BM}}{{ME}}\) \(\widehat {DME} = \widehat {ABC}\) (gt) \( \Rightarrow \Delta BDM\backsim\Delta MDE\;(c - g - c)\) \( \Rightarrow \widehat {BDM} = \widehat {MDE}\) (hai góc tương ứng)
|
