Trắc nghiệm Bài 5: Phương trình chứa dấu giá trị tuyệt đối Toán 8Đề bài
Câu 1 :
Phương trình \(\left| {2x - 5} \right| = 3\) có nghiệm là:
Câu 2 :
Phương trình \(2.\left| {3 - 4x} \right| + 6 = 10\) có nghiệm là
Câu 3 :
Tập nghiệm của phương trình \(\left| {5x - 3} \right| = x + 7\) là
Câu 4 :
Số nghiệm của phương trình \(\left| {x - 3} \right| + 3x = 7\) là
Câu 5 :
Phương trình nào sau đây vô nghiệm?
Câu 6 :
Cho các khẳng định sau: (1) \(\left| {x - 3} \right| = 1\) chỉ có một nghiệm là x = 2 (2) $x = 4$ là nghiệm của phương trình \(\left| {x - 3} \right| = 1\) (3) \(\left| {x - 3} \right| = 1\) có hai nghiệm là $x = 2$ và $x = 4$ Các khẳng định đúng là:
Câu 7 :
Nghiệm nhỏ nhất của phương trình \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\) là
Câu 8 :
Tổng các nghiệm của phương trình \(\left| {3x - 1} \right| = x + 4\) là
Câu 9 :
Nghiệm lớn nhất của phương trình \(\left| {2x} \right| = 3 - 3x\) là
Câu 10 :
Số nghiệm của phương trình \(\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\) là
Câu 11 :
Cho hai phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\) và \(\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\,\left( 2 \right)\). Kết luận nào sau đây là đúng.
Câu 12 :
Tập nghiệm của bất phương trình \(\left| {1 - x} \right| \ge 3\) là
Câu 13 :
Số nguyên dương lớn nhất thỏa mãn bất phương trình \(\left| {x - 6} \right| + 5 \ge x\) là
Câu 14 :
Nghiệm của phương trình \(\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\) là
Lời giải và đáp án
Câu 1 :
Phương trình \(\left| {2x - 5} \right| = 3\) có nghiệm là:
Đáp án : C Phương pháp giải :
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) Lời giải chi tiết :
\(\left| {2x - 5} \right| = 3\) TH1: \(\left| {2x - 5} \right| = 2x - 5\) khi \(2x - 5 \ge 0 \Leftrightarrow 2x \ge 5 \Leftrightarrow x \ge \dfrac{5}{2}\) Khi đó \(\left| {2x - 5} \right| = 3\)$ \Rightarrow 2x - 5 = 3 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\,\left( {TM} \right)$ TH1: \(\left| {2x - 5} \right| = - \left( {2x - 5} \right)\) khi \(2x - 5 < 0 \Leftrightarrow 2x < 5 \Leftrightarrow x < \dfrac{5}{2}\) Khi đó \(\left| {2x - 5} \right| = 3\)$ \Rightarrow - \left( {2x - 5} \right) = 3 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\,\left( {TM} \right)$ Vậy phương trình có nghiệm là \(x = 4;\,x = 1\) .
Câu 2 :
Phương trình \(2.\left| {3 - 4x} \right| + 6 = 10\) có nghiệm là
Đáp án : B Phương pháp giải :
+ Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Sau đó giải phương trình thu được. Lời giải chi tiết :
TH1: \(\left| {3 - 4x} \right| = 3 - 4x\) khi \(3 - 4x \ge 0 \Leftrightarrow 4x \le 3 \Leftrightarrow x \le \dfrac{3}{4}\) Phương trình đã cho trở thành \(2\left( {3 - 4x} \right) + 6 = 10 \)\(\Leftrightarrow 2\left( {3 - 4x} \right) = 4 \)\(\Leftrightarrow 3 - 4x = 2 \)\(\Leftrightarrow x = \dfrac{1}{4}\,\left( {TM} \right)\) TH2: \(\left| {3 - 4x} \right| = - \left( {3 - 4x} \right)\) khi \(3 - 4x < 0 \)\(\Leftrightarrow 4x > 3\)\( \Leftrightarrow x > \dfrac{3}{4}\) Phương trình đã cho trở thành \(2\left( {4x - 3} \right) + 6 = 10 \)\(\Leftrightarrow 2\left( {4x - 3} \right) = 4 \)\(\Leftrightarrow 4x - 3 = 2 \)\(\Leftrightarrow x = \dfrac{5}{4}\,\left( {TM} \right)\) Phương trình có nghiệm \(x = \dfrac{1}{4};\,x = \dfrac{5}{4}\) .
Câu 3 :
Tập nghiệm của phương trình \(\left| {5x - 3} \right| = x + 7\) là
Đáp án : D Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {5x - 3} \right| = 5x - 3\) nếu \(5x - 3 \ge 0 \Leftrightarrow 5x \ge 3 \Leftrightarrow x \ge \dfrac{3}{5}\) Phương trình đã cho trở thành \(5x - 3 = x + 7 \)\(\Leftrightarrow 4x = 10 \)\(\Leftrightarrow x = \dfrac{5}{2}\,\left( {TM} \right)\) . TH2: \(\left| {5x - 3} \right| = - \left( {5x - 3} \right)\) nếu \(5x - 3 < 0 \)\(\Leftrightarrow 5x < 3 \)\(\Leftrightarrow x < \dfrac{3}{5}\) Phương trình đã cho trở thành \( - \left( {5x - 3} \right) = x + 7 \)\(\Leftrightarrow - 6x = 4 \)\(\Leftrightarrow x = - \dfrac{2}{3}\,\left( {TM} \right).\) Vậy tập nghiệm của phương trình \(S = \left\{ {\dfrac{5}{2}; - \dfrac{2}{3}} \right\}\) .
Câu 4 :
Số nghiệm của phương trình \(\left| {x - 3} \right| + 3x = 7\) là
Đáp án : D Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {x - 3} \right| = x - 3\) khi \(x - 3 \ge 0 \Leftrightarrow x \ge 3\) Phương trình đã cho trở thành \(x - 3 + 3x = 7\)\( \Leftrightarrow 4x = 10 \)\(\Leftrightarrow x = \dfrac{5}{2}\,\left( {KTM} \right)\) TH2: \(\left| {x - 3} \right| = - \left( {x - 3} \right)\) khi \(x - 3 < 0 \)\(\Leftrightarrow x < 3\) Phương trình đã cho trở thành \( - \left( {x - 3} \right) + 3x = 7 \)\(\Leftrightarrow 2x = 4 \)\(\Leftrightarrow x = 2\,\left( {TM} \right)\) Vậy phương trình có một nghiệm \(x = 2\).
Câu 5 :
Phương trình nào sau đây vô nghiệm?
Đáp án : B Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right.\) để giải các phương trình. + Lưu ý: \(\left| a \right| \ge 0;\,\forall a\) . Lời giải chi tiết :
* Xét \(\left| {x - 1} \right| = 1\) TH1: \(\left| {x - 1} \right| = x - 1\) khi \(x \ge 1\) , nên ta có phương trình \(x - 1 = 1 \Leftrightarrow x = 2\left( {TM} \right)\) TH2: \(\left| {x - 1} \right| = 1 - x\) khi \(x < 1\) , nên ta có phương trình \(1 - x = 1 \Leftrightarrow x = 0\,\left( {TM} \right)\) Vậy \(S = \left\{ {0;2} \right\}\) * Xét \(\left| {x + 3} \right| = 0 \Leftrightarrow x + 3 = 0 \Rightarrow x = - 3\) nên \(S = \left\{ { - 3} \right\}\) * Xét \(\left| {2x} \right| = 10\) TH1: \(\left| {2x} \right| = 2x\) khi \(x \ge 0\) nên ta có phương trình \(2x = 10 \Leftrightarrow x = 5\,\left( {TM} \right)\) TH2: \(\left| {2x} \right| = - 2x\) khi \(x < 0\) nên ta có phương trình \( - 2x = 10 \Leftrightarrow x = - 5\,\left( {TM} \right)\) Vậy \(S = \left\{ {5; - 5} \right\}\) * Xét \(\left| x \right| = - 9\). Thấy rằng \(\left| x \right| \ge 0;\,\forall x\) mà \( - 9 < 0\) nên \(\left| x \right| > - 9\) với mọi \(x\). Hay phương trình \(\left| x \right| = - 9\) vô nghiệm.
Câu 6 :
Cho các khẳng định sau: (1) \(\left| {x - 3} \right| = 1\) chỉ có một nghiệm là x = 2 (2) $x = 4$ là nghiệm của phương trình \(\left| {x - 3} \right| = 1\) (3) \(\left| {x - 3} \right| = 1\) có hai nghiệm là $x = 2$ và $x = 4$ Các khẳng định đúng là:
Đáp án : B Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Lời giải chi tiết :
Xét phương trình \(\left| {x - 3} \right| = 1\) TH1: \(\left| {x - 3} \right| = x - 3\) khi \(x - 3 \ge 0 \Leftrightarrow x \ge 3\) Phương trình đã cho trở thành \(x - 3 = 1 \Leftrightarrow x = 4\left( {TM} \right)\) TH2: \(\left| {x - 3} \right| = 3 - x\) khi \(x - 3 < 0 \Leftrightarrow x < 3\) Phương trình đã cho trở thành \(3 - x = 1 \Leftrightarrow x = 2\left( {TM} \right)\) Vậy phương trình \(\left| {x - 3} \right| = 1\) có hai nghiệm \(x = 2;x = 4\). Nên \(x = 4\) là nghiệm của phương trình \(\left| {x - 3} \right| = 1\). Khẳng định đúng là (2) và (3).
Câu 7 :
Nghiệm nhỏ nhất của phương trình \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\) là
Đáp án : A Phương pháp giải :
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\) Ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\) Lời giải chi tiết :
Ta có \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\)\( \Leftrightarrow \left[ \begin{array}{l}2 + 3x = 4x - 3\\2 + 3x = 3 - 4x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\7x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = \dfrac{1}{7}\end{array} \right.\) Vậy nghiệm nhỏ nhất của phương trình là \(x = \dfrac{1}{7}\) .
Câu 8 :
Tổng các nghiệm của phương trình \(\left| {3x - 1} \right| = x + 4\) là
Đáp án : D Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {3x - 1} \right| = 3x - 1\) khi \(3x - 1 \ge 0 \Leftrightarrow 3x \ge 1 \Leftrightarrow x \ge \dfrac{1}{3}\) Phương trình đã cho trở thành \(3x - 1 = x + 4 \)\(\Leftrightarrow 2x = 5\)\( \Leftrightarrow x = \dfrac{5}{2}\left( {TM} \right)\) TH2: \(\left| {3x - 1} \right| = 1 - 3x\) khi \(3x - 1 < 0 \)\(\Leftrightarrow x < \dfrac{1}{3}\) Phương trình đã cho trở thành \(1 - 3x = x + 4 \)\(\Leftrightarrow 4x = - 3 \)\(\Leftrightarrow x = - \dfrac{3}{4}\,\left( {TM} \right)\) Vậy \(S = \left\{ {\dfrac{{ - 3}}{4};\dfrac{5}{2}} \right\}\) Tổng các nghiệm của phương trình là \( - \dfrac{3}{4} + \dfrac{5}{2} = \dfrac{7}{4}\) .
Câu 9 :
Nghiệm lớn nhất của phương trình \(\left| {2x} \right| = 3 - 3x\) là
Đáp án : C Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {2x} \right| = 2x\) khi \(2x \ge 0 \Leftrightarrow x \ge 0\) Phương trình đã cho trở thành \(2x = 3 - 3x \Leftrightarrow 5x = 3 \Leftrightarrow x = \dfrac{3}{5}\,\left( {TM} \right)\) TH2: \(\left| {2x} \right| = - 2x\) khi \(2x < 0 \Leftrightarrow x < 0\) Phương trình đã cho trở thành \( - 2x = 3 - 3x \Leftrightarrow x = 3\,\left( {KTM} \right)\) Vậy nghiệm lớn nhất của phương trình là \(x = 3\) .
Câu 10 :
Số nghiệm của phương trình \(\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\) là
Đáp án : A Phương pháp giải :
- Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối. - Căn cứ vào bảng xét từng khoảng giải bài toán (đối chiếu với điều kiện tương ứng). Lời giải chi tiết :
Ta có \(\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\,\,\,\,\left( 1 \right)\) Xét: \(\begin{array}{l} + )\;\;1 - x = 0 \Leftrightarrow x = 1\\ + )\;\;2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\end{array}\) Ta có bảng xét dấu đa thức $1 - x$ và $2x - 1$ dưới đây 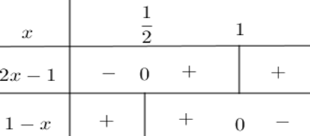 Từ bảng xét dấu ta có: TH1: \(x < \dfrac{1}{2}\) khi đó \(\left| {2x - 1} \right| = 1 - 2x;\,\left| {1 - x} \right| = 1 - x\) nên phương trình \(\left( 1 \right)\) trở thành \(1 - x - \left( {1 - 2x} \right) = x - 2 \Leftrightarrow 1 - x - 1 + 2x = x - 2 \Leftrightarrow x = x - 2\) \( \Leftrightarrow 0 = - 2\) (vô lý) TH2: \(\dfrac{1}{2} \le x \le 1\), khi đó \(\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = 1 - x\) nên phương trình \(\left( 1 \right)\) trở thành \(1 - x - \left( {2x - 1} \right) = x - 2 \Leftrightarrow - 3x + 2 = x - 2 \Leftrightarrow - 4x = - 4 \Leftrightarrow x = 1\,\left( {TM} \right)\) TH3: \(x > 1\) , khi đó \(\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = x - 1\) nên phương trình \(\left( 1 \right)\) trở thành \(x - 1 - \left( {2x - 1} \right) = x - 2 \Leftrightarrow - x = x - 2 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\,\,\left( {L} \right)\) Vậy phương trình có nghiệm \(x = 1\) .
Câu 11 :
Cho hai phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\) và \(\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\,\left( 2 \right)\). Kết luận nào sau đây là đúng.
Đáp án : C Phương pháp giải :
Để giải phương trình \(\left( 1 \right)\) ta thực hiện các bước sau: + Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các phương trình bậc nhất một ẩn + So sánh với điều kiện và kết luận. Để giải phương trình \(\left( 2 \right)\), ta chuyển vế biến đổi phương trình về dạng \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right.\) Lời giải chi tiết :
* Xét phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\) TH1: \(\left| {2x - 1} \right| = 2x - 1\) khi \(x \ge \dfrac{1}{2}\) Phương trình \(\left( 1 \right)\) trở thành \(4\left( {2x - 1} \right) + 3 = 15 \)\(\Leftrightarrow 4\left( {2x - 1} \right) = 12 \)\(\Leftrightarrow 2x - 1 = 3 \)\(\Leftrightarrow x = 2\,\left( {TM} \right)\) TH2: \(\left| {2x - 1} \right| = 1 - 2x\) khi \(x < \dfrac{1}{2}\) Phương trình \(\left( 1 \right)\) trở thành \(4\left( {1 - 2x} \right) + 3 = 15 \)\(\Leftrightarrow 4\left( {1 - 2x} \right) = 12 \)\(\Leftrightarrow 1 - 2x = 3 \)\( \Leftrightarrow x = - 1\left( {TM} \right)\) Vậy phương trình \(\left( 1 \right)\) có hai nghiệm \(x = - 1;\,x = 2\). Xét phương trình \(\;\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\\ \Leftrightarrow \left| {7x + 1} \right| = \left| {5x + 6} \right|\\ \Leftrightarrow \left[ \begin{array}{l}7x + 1 = 5x + 6\\7x + 1 = - (5x + 6)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 5\\12x = - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{2}\\x = - \dfrac{7}{{12}}\end{array} \right.\) Vậy phương trình \(\left( 2 \right)\) có hai nghiệm là \(x = \dfrac{5}{2};x = - \dfrac{7}{{12}}.\)
Câu 12 :
Tập nghiệm của bất phương trình \(\left| {1 - x} \right| \ge 3\) là
Đáp án : A Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các bất phương trình bậc nhất một ẩn + Kết hợp với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {1 - x} \right| = 1 - x\) với \(1 - x \ge 0 \Leftrightarrow x \le 1\) Bất phương trình đã cho trở thành \(1 - x \ge 3 \Leftrightarrow x \le - 2\), kết hợp điều kiện \(x \le 1\) ta có \(x \le - 2\). TH2: \(\left| {1 - x} \right| = x - 1\) với \(1 - x < 0 \Leftrightarrow x > 1\) Bất phương trình đã cho trở thành \(x - 1 \ge 3 \Leftrightarrow x \ge 4\), kết hợp điều kiện \(x > 1\) ta có \(x \ge 4\). Vậy bất phương trình có nghiệm \(x \ge 4,x \le - 2\)
Câu 13 :
Số nguyên dương lớn nhất thỏa mãn bất phương trình \(\left| {x - 6} \right| + 5 \ge x\) là
Đáp án : B Phương pháp giải :
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) + Giải các bất phương trình bậc nhất một ẩn + Kết hợp với điều kiện và kết luận. Lời giải chi tiết :
TH1: \(\left| {x - 6} \right| = x - 6\) với \(x - 6 \ge 0 \Leftrightarrow x \ge 6\) Bất phương trình đã cho trở thành \(x - 6 + 5 \ge x \Leftrightarrow - 1 \ge 0\) (vô lý) TH2: \(\left| {x - 6} \right| = 6 - x\) với \(x - 6 < 0 \Leftrightarrow x < 6\). Bất phương trình đã cho trở thành \(6 - x + 5 \ge x \)\(\Leftrightarrow - 2x \ge - 11 \)\(\Leftrightarrow x \le \dfrac{{11}}{2}\), kết hợp điều kiện \(x < 6\) ta có \(x \le \dfrac{{11}}{2}\). Bất phương trình có tập nghiệm \(S = \left\{ x \in R|{x \le \dfrac{{11}}{2}} \right\}\). Nghiệm nguyên dương lớn nhất thỏa mãn là \(x = 5\).
Câu 14 :
Nghiệm của phương trình \(\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\) là
Đáp án : A Phương pháp giải :
Với \(\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\)\( \Rightarrow x \ge 0\) Bỏ dấu giá trị tuyệt đối ta được phương trình: \(x + \dfrac{1}{{209}} + x + \dfrac{2}{{209}} + ..... + x + \dfrac{{208}}{{209}} = 209x.\) Lời giải chi tiết :
Điều kiện \(209x \ge 0 \Leftrightarrow x \ge 0\) $\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\\ \Leftrightarrow x + \dfrac{1}{{209}} + x + \dfrac{2}{{209}} + x + \dfrac{3}{{209}} + ... + x + \dfrac{{100}}{{209}} = 209x\\ \Leftrightarrow 208x + \left( {\dfrac{1}{{209}} + \dfrac{2}{{209}} + \dfrac{3}{{209}} + ... + \dfrac{{208}}{{209}}} \right) = 209x\\ \Leftrightarrow 208x + \dfrac{{104.209}}{{209}} = 209x\\ \Leftrightarrow 208x + 104 = 209x\\ \Leftrightarrow x = 104\;\;(TM)$ Vậy \(x = 104.\)
|
