Trắc nghiệm Bài 8: Các trường hợp đồng dạng của tam giác vuông Toán 8Đề bài
Câu 1 :
Cho các mệnh đề sau. Chọn câu đúng. (I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. (II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Câu 2 :
Cho hình vẽ dưới đây với \(\widehat {BAH} = \widehat {ACH}\) . 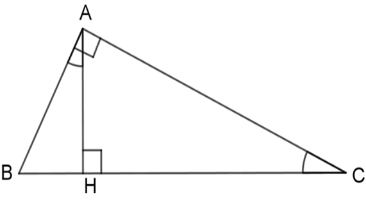 Khi đó các mệnh đề (I) \(\Delta AHB\backsim\Delta CHA\;(g - g)\) (II) \(\Delta AHC\backsim\Delta BAC\;(g - g)\)
Câu 3 :
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau: (I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$. (II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$. (III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$. (IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
Câu 4 :
Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.
Câu 5 :
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
Câu 6 :
Cho tam giác $ABC$ cân tại $A$ , $AC = 20{\rm{cm}}$, $BC = 24{\rm{cm}}$, các đường cao $AD$ và $CE$ cắt nhau ở $H$ . Tính độ dài \(HD\) .
Câu 7 :
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?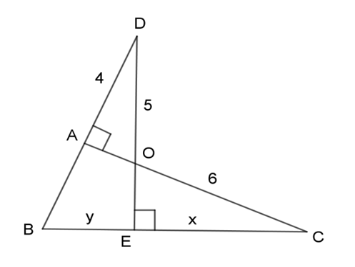 
Cho tam giác $ABC$ vuông ở $A$ , đường cao $AH$ . Câu 8
Tích \(HB.HC\) bằng
Câu 9
Cho $BH = 9cm,HC = 16cm$ . Tính diện tích của tam giác \(ABC\) .
Cho tam giác $ABC$ vuông ở $A,AB = 6cm,AC = 8cm$ , đường cao $AH$ , đường phân giác $BD$ . Câu 10
Tính độ dài các đoạn $AD,DC$ lần lượt là
Câu 11
Gọi $I$ là giao điểm của $AH$ và $BD$ . Chọn câu đúng.
Câu 12 :
Cho tam giác $ABC$, phân giác $AD$ . Gọi $E,F$ lần lượt là hình chiếu của $B$ và $C$ lên $AD$ . Chọn khẳng định đúng.
Câu 13 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ chia cạnh $BC$ thành hai đoạn thẳng $HB = 7$cm và $HC = 18$cm. Điểm $E$ thuộc đoạn thẳng $HC$ sao cho đường thẳng đi qua $E$ và vuông góc với $BC$ chia tam giác $ABC$ thành hai phần có diện tích bằng nhau. Tính $CE$.
Lời giải và đáp án
Câu 1 :
Cho các mệnh đề sau. Chọn câu đúng. (I) Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. (II) Nếu một góc của tam giác vuông này lớn hơn một góc của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Đáp án : A Lời giải chi tiết :
Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. Vậy (I) đúng, (II) sai.
Câu 2 :
Cho hình vẽ dưới đây với \(\widehat {BAH} = \widehat {ACH}\) . Khi đó các mệnh đề (I) \(\Delta AHB\backsim\Delta CHA\;(g - g)\) (II) \(\Delta AHC\backsim\Delta BAC\;(g - g)\)
Đáp án : D Phương pháp giải :
- Áp dụng lý thuyết về các trường hợp đồng dạng của tam giác vuông để chứng minh các cặp tam giác vuông đồng dạng với nhau, từ đó chọn đáp án đúng. Lời giải chi tiết :
Xét $2$ tam giác vuông $AHB$ và $CHA$ có: \(\widehat {BAH} = \widehat {ACH}\) (gt) \( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\) \( \Rightarrow \) (I) đúng. Xét $2$ tam giác vuông $AHC$ và $BAC$ có: \(\widehat C\) chung \( \Rightarrow \Delta AHC\backsim\Delta BAC\;(g - g)\) \( \Rightarrow \) (II) đúng. Vậy cả (I) và (II) đều đúng.
Câu 3 :
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau: (I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$. (II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$. (III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$. (IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
Đáp án : A Phương pháp giải :
Sử dụng tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng. Nếu hai tam giác đồng dạng thì: + Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng; + Tỉ số hai diện tích bằng bình phương tỉ số đồng dạng. Lời giải chi tiết :
Vì $\Delta DHE\backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$ nên tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$ và tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là ${\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}$ Do đó (I) và (IV) đúng, (II) và (III) sai.
Câu 4 :
Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.
Đáp án : B Phương pháp giải :
- Kẻ đường cao \(AD\) sau đó chứng minh hai tam giác đồng dạng để suy ra tỉ lệ cạnh thích hợp, từ đó tính \(AB\) . Lời giải chi tiết :
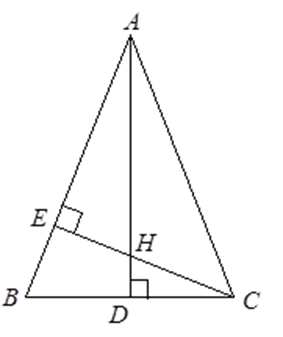 Kẻ đường cao $AD$ . Xét \(\Delta CBE\) và \(\Delta ABD\) có \(\widehat {BEC} = \widehat {ADB} = 90^\circ \) và \(\widehat B\) chung nên $\Delta CBE\backsim\Delta ABD$ (g.g) $ \Rightarrow \dfrac{{BC}}{{AB}} = \dfrac{{BE}}{{BD}}$ hay $\dfrac{{24}}{{AB}} = \dfrac{9}{{12}}$ $ \Rightarrow AB = 32{\rm{cm}}$.
Câu 5 :
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
Đáp án : D Phương pháp giải :
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp. - Tính độ dài các cạnh cần tìm dựa vào định lý Pitago và dữ kiện đã có. Lời giải chi tiết :
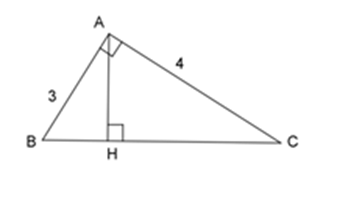 Áp dụng định lý Pytago vào tam giác vuông $ABC$ ta có: \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {3^2} + {4^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 25\\ \Rightarrow BC = 5\;cm\end{array}\) Xét 2 tam giác vuông $ABC$ và $HBA$ có: \(\widehat B\) chung \( \Rightarrow \Delta ABC\backsim\Delta HBA\;(g - g)\) \( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\;cm\) Mặt khác: \(\dfrac{{AB}}{{HB}} = \dfrac{{AC}}{{HA}} \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\;cm\) Nên \(HA = 2,4\,cm;\,HB = 1,8\,cm\) .
Câu 6 :
Cho tam giác $ABC$ cân tại $A$ , $AC = 20{\rm{cm}}$, $BC = 24{\rm{cm}}$, các đường cao $AD$ và $CE$ cắt nhau ở $H$ . Tính độ dài \(HD\) .
Đáp án : C Phương pháp giải :
Bước 1: Tính \(AD\) theo định lý Pytago Bước 2: Chứng minh hai tam giác đồng dạng $\Delta CDH$ và $\Delta ADB$ (góc-góc). Từ đó tính đoạn \(HD\) . Lời giải chi tiết :
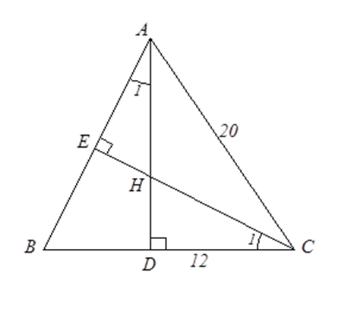 Tam giác $ABC$ cân tại $A$ nên $BD = DC = \dfrac{{BC}}{2} = \dfrac{{24}}{2} = 12\left( {{\rm{cm}}} \right)$. Theo định lý Py-ta-go, ta có $A{D^2} = A{C^2} - D{C^2} = {20^2} - {12^2} = {16^2}$ nên $AD = 16{\rm{cm}}$. Xét $\Delta CDH$ và $\Delta ADB$ có $\widehat {CDH} = \widehat {ADB} = {90^o}$ . $\widehat {{C_1}} = \widehat {{A_1}}$ (cùng phụ với $\widehat B$). Do đó \(\Delta CDH\backsim\Delta ADB\) (g.g) Nên $\dfrac{{HD}}{{BD}} = \dfrac{{HC}}{{AB}} = \dfrac{{CD}}{{AD}}$, tức là $\dfrac{{HD}}{{12}} = \dfrac{{HC}}{{20}} = \dfrac{{12}}{{16}} = \dfrac{3}{4}$ Suy ra $HD = 9{\rm{cm}}$.
Câu 7 :
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?
Đáp án : B Phương pháp giải :
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp. - Tính độ dài $x,y$ dựa vào dữ kiện tìm được và dữ kiện đề bài đã cho (áp dụng định lý Pytago). Lời giải chi tiết :
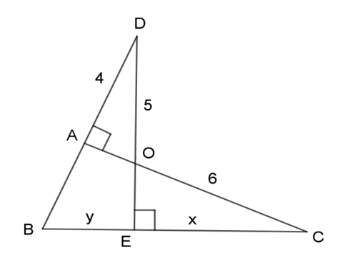 Xét 2 tam giác vuông \(\Delta ADO\)\((\widehat {DAO} = {90^0})\) và \(\Delta ECO\)\((\widehat {CEO} = {90^0})\) ta có: \(\widehat {AOD} = \widehat {EOC}\) (2 góc đối đỉnh) \( \Rightarrow \Delta ADO\backsim\Delta ECO\;(g - g)\) \( \Rightarrow \dfrac{{AD}}{{EC}} = \dfrac{{DO}}{{CO}} \Leftrightarrow \dfrac{4}{x} = \dfrac{5}{6} \Leftrightarrow x = \dfrac{{4.6}}{5} = 4,8\) Vì \(\Delta ADO\) vuông tại A nên áp dụng định lý Pitago ta có: \(\begin{array}{l}\,\,\,\,\,\,\,\,A{D^2} + A{O^2} = O{D^2}\\ \Leftrightarrow {4^2} + A{O^2} = {5^2}\\ \Leftrightarrow A{O^2} = {5^2} - {4^2} = 9\\ \Rightarrow AO = 3\end{array}\) Xét 2 tam giác vuông \(\Delta CEO\;(\widehat {CEO} = {90^0})\) và \(\Delta CAB\;(\widehat {CAB} = {90^0})\) có:\(\widehat C\) chung
\( \Rightarrow \dfrac{{CO}}{{CB}} = \dfrac{{CE}}{{CA}} \Leftrightarrow \dfrac{{CO}}{{CE + EB}} = \dfrac{{CE}}{{CO + OA}} \Leftrightarrow \dfrac{6}{{4,8 + y}} = \dfrac{{4,8}}{{6 + 3}} \Leftrightarrow y = 6,45\) Vậy \(x = 4,8;\;y = 6,45\). Cho tam giác $ABC$ vuông ở $A$ , đường cao $AH$ . Câu 8
Tích \(HB.HC\) bằng
Đáp án : B Phương pháp giải :
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp. Lời giải chi tiết :
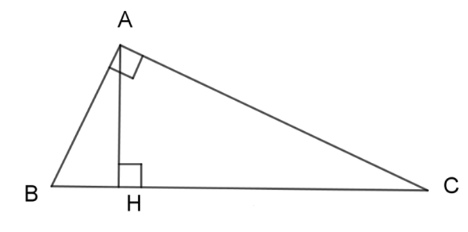 Ta có: \(\widehat {HAB} + \widehat {HAC} = \widehat {BAC} = {90^0}\) Mà: \(\widehat {HBA} + \widehat {HAB} = {90^0}\) (2 góc phụ nhau) \( \Rightarrow \widehat {HAC} = \widehat {HBA}\) Xét 2 tam giác vuông AHB và CHA ta có: \(\widehat {HAC} = \widehat {HBA}\) (cmt) \( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\) \( \Rightarrow \dfrac{{AH}}{{CH}} = \dfrac{{HB}}{{HA}} \Leftrightarrow A{H^2} = HB.HC\) Câu 9
Cho $BH = 9cm,HC = 16cm$ . Tính diện tích của tam giác \(ABC\) .
Đáp án : C Phương pháp giải :
- Tính độ dài các cạnh cần thiết dựa vào định lý Pytago và dữ kiện đã có. - Tính diện tích tam giác \(ABC\) . Lời giải chi tiết :
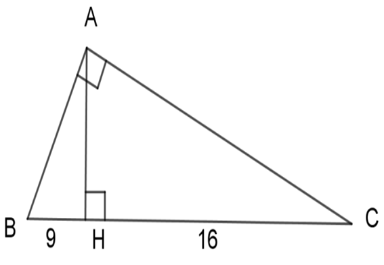 Với $BH = 9cm,HC = 16cm$ . \( \Rightarrow BC = BH + HC \)\(= 9 + 16 = 25\;cm\) Ta có: \(A{H^2} = HB.HC\) (cmt) \(\begin{array}{l} \Rightarrow A{H^2} = 9.16 = 144\\ \Rightarrow AH = 12\;cm\end{array}\) Nên diện tích tam giác \(ABC\) là \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.12.25 = 150\,c{m^2}\) . Cho tam giác $ABC$ vuông ở $A,AB = 6cm,AC = 8cm$ , đường cao $AH$ , đường phân giác $BD$ . Câu 10
Tính độ dài các đoạn $AD,DC$ lần lượt là
Đáp án : D Phương pháp giải :
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp. - Tính độ dài các cạnh cần tìm dựa vào định lý Pytago và dữ kiện đã có. Lời giải chi tiết :
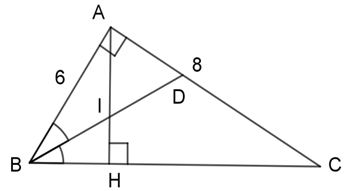 + Áp dụng định lý Pitago trong tam giác vuông $ABC$ ta có: \(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {6^2} + {8^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 100\\ \Rightarrow BC = 10\;cm\end{array}\) + Vì $BD$ là đường phân giác của tam giác $ABC$ nên áp dụng tính chất đường phân giác của tam giác, ta có: \(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\\ \Leftrightarrow \dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CA - AD}}\)\( \Leftrightarrow \dfrac{6}{{AD}} = \dfrac{{10}}{{8 - AD}}\\ \Rightarrow AD = 3\;cm\\ \Rightarrow DC = AC - AD \)\(= 8 - 3 = 5\;cm\) Câu 11
Gọi $I$ là giao điểm của $AH$ và $BD$ . Chọn câu đúng.
Đáp án : A Phương pháp giải :
Từ dữ kiện đã có suy ra hai tam giác đồng dạng từ đó có tỉ lệ cạnh cần tìm. Lời giải chi tiết :
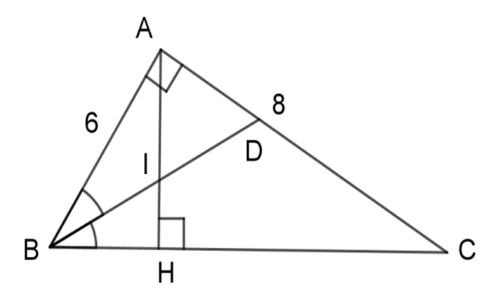 Xét 2 tam giác vuông $ABD$ và $HBI$ có: \(\widehat {ABD} = \widehat {HBI}\) ($BD$ là tia phân giác của góc $B$ ) \( \Rightarrow \Delta ABD\backsim\Delta HBI\;(g - g)\) \( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BD}}{{BI}}\)\( \Leftrightarrow AB.BI = BD.HB\;\)
Câu 12 :
Cho tam giác $ABC$, phân giác $AD$ . Gọi $E,F$ lần lượt là hình chiếu của $B$ và $C$ lên $AD$ . Chọn khẳng định đúng.
Đáp án : C Phương pháp giải :
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp. - Từ đó rút ra điều cần chứng minh. Lời giải chi tiết :
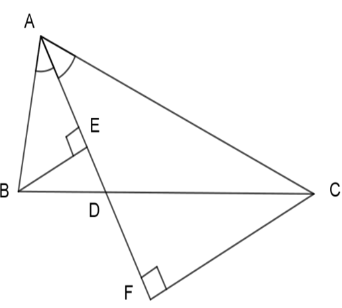 Xét 2 tam giác vuông ABE và ACF ta có: \(\widehat {BAE} = \widehat {CAF}\) (vì AD là tia phân giác của góc A) \( \Rightarrow \Delta ABE\backsim\Delta ACF\;(g - g)\) \( \Rightarrow \dfrac{{AE}}{{AF}} = \dfrac{{BE}}{{CF}}\;(1)\) Xét 2 tam giác vuông BDE và CDF ta có: \(\widehat {EDB} = \widehat {FDC}\) (2 góc đối đỉnh) \( \Rightarrow \Delta BDE\backsim\Delta CDF\)(g – g) \( \Rightarrow \dfrac{{BE}}{{CF}} = \dfrac{{DE}}{{DF}}\;(2)\) Từ (1) và (2) ta có: \(\dfrac{{AE}}{{AF}} = \dfrac{{DE}}{{DF}} \Leftrightarrow AE.DF = AF.DE\) (đpcm)
Câu 13 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ chia cạnh $BC$ thành hai đoạn thẳng $HB = 7$cm và $HC = 18$cm. Điểm $E$ thuộc đoạn thẳng $HC$ sao cho đường thẳng đi qua $E$ và vuông góc với $BC$ chia tam giác $ABC$ thành hai phần có diện tích bằng nhau. Tính $CE$.
Đáp án : A Phương pháp giải :
Bước 1: Gọi $D$ là giao điểm của $AC$ và đường vuông góc với $BC$ tại $E$. Bước 2: Sử dụng cặp tam giác đồng dạng và tỉ số diện tích của hai tam giác đồng dạng để tính toán. Lời giải chi tiết :
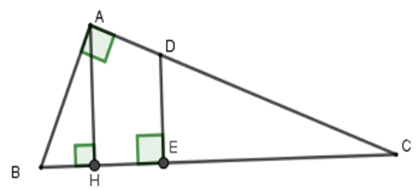 Gọi $D$ là giao điểm của $AC$ và đường vuông góc với $BC$ tại $E$. Xét \(\Delta AHC\) và \(\Delta ABC\) có \(\widehat C\) chung và \(\widehat {AHC} = \widehat {BAC} = 90^\circ \) nên \(\Delta AHC\backsim\Delta BAC\,\left( {g - g} \right)\) Ta có ${S_{DEC}} = \dfrac{1}{2}{S_{ABC}}$ (1), ${S_{AHC}}:{S_{ABC}} = \dfrac{{HC}}{{BC}} = \dfrac{{18}}{{25}}$ (2). Từ (1) và (2) suy ra ${S_{DEC}}:{S_{AHC}} = \dfrac{1}{2}:\dfrac{{18}}{{25}} = \dfrac{{25}}{{36}} = {\left( {\dfrac{5}{6}} \right)^2}$ (3). Vì \(DE{\rm{//}}AH\) (cùng vuông với \(BC\) ) suy ra $\Delta DEC\backsim\Delta AHC$ nên ${S_{DEC}}:{S_{AHC}} = {\left( {\dfrac{{EC}}{{HC}}} \right)^2}$ (4). Từ (3) và (4) suy ra $\dfrac{{EC}}{{HC}} = \dfrac{5}{6}$ tức là $\dfrac{{EC}}{{18}} = \dfrac{5}{6} \Rightarrow EC = 15\,{\rm{cm}}$.
|
