Trắc nghiệm Bài 1: Tứ giác Toán 8Đề bài
Câu 1 :
Hãy chọn câu sai.
Câu 2 :
Cho hình vẽ dưới đây. Chọn khẳng định sai.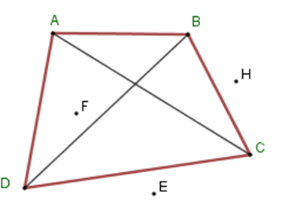 
Câu 3 :
Cho hình vẽ sau. Chọn câu sai.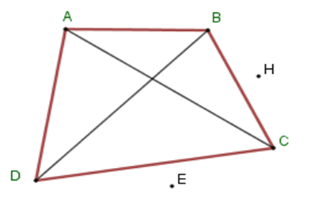 
Câu 4 :
Cho tứ giác \(ABCD\) có \(\widehat A = {60^0};\;\widehat B = {135^0};\;\widehat D = {29^0}\) . Số đo góc $C$ bằng:
Câu 5 :
Cho tứ giác $ABCD$ có \(\widehat A = {50^0};\;\widehat C = {150^0};\;\widehat D = {45^0}\). Số đo góc ngoài tại đỉnh $B$ bằng:
Câu 6 :
Cho tứ giác \(ABCD\) . Tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là
Câu 7 :
Cho tứ giác \(ABCD\) có \(\widehat A = 100^\circ \) . Tổng số đo các góc ngoài đỉnh $B,C,D$ bằng:
Câu 8 :
Tứ giác $ABCD$ có \(AB = BC,CD = DA,\;\widehat B = {90^0};\;\widehat D = {120^0}\). Hãy chọn câu đúng nhất:
Câu 9 :
Cho tứ giác$ABCD$. Gọi $O$ là giao điểm của hai đường chéo $AC$ và$BD$ . Khẳng định nào sau đây là đúng nhất.
Câu 10 :
Cho tứ giác \(ABCD\) biết số đo của các góc \(\widehat A;\,\widehat B;\,\widehat C;\,\widehat D\) tỉ lệ thuận với $4;3;5;6.$ Khi đó số đo các góc \(\widehat A;\,\widehat B;\,\widehat C;\,\widehat D\) lần lượt là:
Câu 11 :
Tam giác \(ABC\) có \(\widehat A = 60^\circ \), các tia phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Các tia phân giác góc ngoài tại đỉnh \(B\) và \(C\) cắt nhau tại \(K\). Tính các góc \(\widehat {BIC};\,\widehat {BKC}.\)
Câu 12 :
Tứ giác \(ABCD\) có \(\widehat C + \widehat D = 90^\circ .\) Chọn câu đúng.
Câu 13 :
Tứ giác \(ABCD\) có \(\widehat A - \widehat C = 60^\circ .\) Các tia phân giác của các góc \(B\) và \(D\) cắt nhau tại \(I.\) Tính số đo góc \(BID.\)
Lời giải và đáp án
Câu 1 :
Hãy chọn câu sai.
Đáp án : B Lời giải chi tiết :
Định lý: Tổng các góc của một tứ giác bằng \({360^0}\) nên C đúng, B sai.
Câu 2 :
Cho hình vẽ dưới đây. Chọn khẳng định sai.
Đáp án : D Phương pháp giải :
Ta sử dụng kiến thức về các yếu tố góc, đỉnh, cạnh của tứ giác \(ABCD\). Lời giải chi tiết :
Từ hình vẽ ta thấy các điểm \(E,\,H\) nằm bên ngoài tứ giác và điểm \(F\) nằm bên trong tứ giác\(ABCD\) nên D sai.
Câu 3 :
Cho hình vẽ sau. Chọn câu sai.
Đáp án : C Phương pháp giải :
Ta sử dụng kiến thức về các yếu tố góc, đỉnh, cạnh của tứ giác \(ABCD\). Lời giải chi tiết :
Tứ giác \(ABCD\) có các cặp góc đối nhau là \(\widehat A;\,\widehat C\) và \(\widehat B;\,\widehat D\) còn \(\widehat A;\,\widehat B\) là hai góc kề nhau nên C sai.
Câu 4 :
Cho tứ giác \(ABCD\) có \(\widehat A = {60^0};\;\widehat B = {135^0};\;\widehat D = {29^0}\) . Số đo góc $C$ bằng:
Đáp án : B Phương pháp giải :
Ta sử dụng định lý về tổng các góc trong tứ giác. Định lý: Tổng các góc của một tứ giác bằng \(360^\circ \) . Lời giải chi tiết :
Xét tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)(định lý) hay \(60^\circ + 135^\circ + \widehat C + 29^\circ = 360^\circ \Rightarrow \widehat C = 360^\circ - 60^\circ - 135^\circ - 29^\circ \) \( \Leftrightarrow \widehat C = 136^\circ \) .
Câu 5 :
Cho tứ giác $ABCD$ có \(\widehat A = {50^0};\;\widehat C = {150^0};\;\widehat D = {45^0}\). Số đo góc ngoài tại đỉnh $B$ bằng:
Đáp án : A Phương pháp giải :
+ Ta sử dụng định lý về tổng các góc trong tứ giác: Tổng các góc của một tứ giác bằng \(360^\circ \) để tính góc \(B\) + Từ đó suy ra số đo góc ngoài tại \(B\) là \(180^\circ - \widehat B\) . Lời giải chi tiết :
Xét tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \) (định lý) Hay \(50^\circ + \widehat B + 150^\circ + 45^\circ = 360^\circ \) \(\widehat B = 360^\circ - 50^\circ - 150^\circ - 45^\circ \) Nên góc ngoài tại đỉnh $B$ có số đo là \(180^\circ - \widehat B = 180^\circ - 115^\circ = 65^\circ \) .
Câu 6 :
Cho tứ giác \(ABCD\) . Tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là
Đáp án : D Phương pháp giải :
Ta sử dụng định nghĩa: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác. Và định lý: Tổng bốn góc của một tứ giác bằng ${360^0}$ . Lời giải chi tiết :
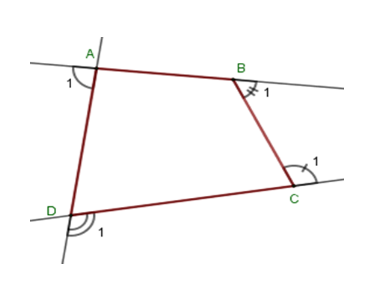 Gọi góc ngoài tại bốn đỉnh \(A,B,\,C,\,D\) của tứ giác \(ABCD\) lần lượt là \(\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}\) . Khi đó ta có \(\widehat A + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - \widehat A\); \(\widehat B + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - \widehat B\); \(\widehat C + \widehat {{C_1}} = 180^\circ \Rightarrow \widehat {{C_1}} = 180^\circ - \widehat C\) và \(\widehat D + \widehat {{D_1}} = 180^\circ \Rightarrow \widehat {{D_1}} = 180^\circ - \widehat D\) Suy ra \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 180^\circ - \widehat A + 180^\circ - \widehat B + 180^\circ - \widehat C + 180^\circ - \widehat D\) \( = 720^\circ - \left( {\widehat A + \widehat B + \widehat C + \widehat D} \right) = 720^\circ - 360^\circ = 360^\circ \) (Vì \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)) Vậy tổng số đo các góc ngoài tại \(4\) đỉnh \(A,B,\,C,\,D\) là \(360^\circ \) .
Câu 7 :
Cho tứ giác \(ABCD\) có \(\widehat A = 100^\circ \) . Tổng số đo các góc ngoài đỉnh $B,C,D$ bằng:
Đáp án : C Phương pháp giải :
Bước 1: Tính góc ngoài tại đỉnh \(A\) Bước 2: Từ các câu trước ta suy ra “ tổng số đo góc ngoài tại bốn đỉnh của một tứ giác là \(360^\circ \)” . Từ đó tính tổng số đo các góc ngoài đỉnh $B,C,D$ Lời giải chi tiết :
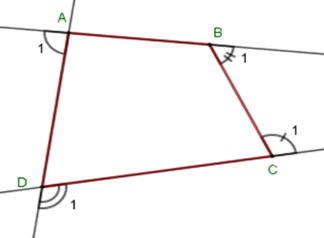 Gọi góc ngoài tại bốn đỉnh \(A,B,\,C,\,D\) của tứ giác \(ABCD\) lần lượt là \(\widehat {{A_1}};\,\widehat {{B_1}};\,\widehat {{C_1}};\,\widehat {{D_1}}\) . Khi đó ta có \(\widehat A + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - \widehat A = 180^\circ - 100^\circ = 80^\circ .\) Theo kết quả các câu trước ta có \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \)\( \Rightarrow \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ - \widehat {{A_1}} = 360^\circ - 80^\circ = 280^\circ \) . Vậy \(\widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 280^\circ \).
Câu 8 :
Tứ giác $ABCD$ có \(AB = BC,CD = DA,\;\widehat B = {90^0};\;\widehat D = {120^0}\). Hãy chọn câu đúng nhất:
Đáp án : D Phương pháp giải :
Ta sử dụng tính chất tam giác vuông cân , tam giác cân và tổng ba góc trong tam giác bằng \(180^\circ \) . Lời giải chi tiết :
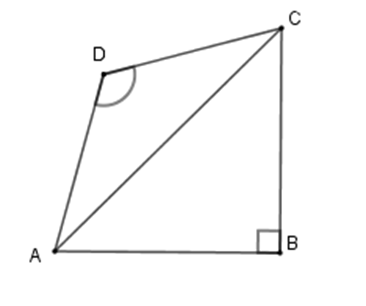 Xét tam giác $ABC$ có \(\widehat B = 90^\circ ;AB = BC \Rightarrow \Delta ABC\) vuông cân \( \Rightarrow \widehat {BAC} = \widehat {BCA} = \dfrac{{90^\circ }}{2} = 45^\circ \) Xét tam giác $ADC$ có \(CD = DA \Rightarrow \Delta ADC\) cân tại \(D\) có \(\widehat {ADC} = 120^\circ \) nên \(\widehat {DAC} = \widehat {DCA} = \dfrac{{180^\circ - 120^\circ }}{2} = 30^\circ \) Từ đó ta có $\widehat A = \widehat {BAD} = \widehat {BAC} + \widehat {CAD} = 45^\circ + 30^\circ = 75^\circ $ Và $\widehat C = \widehat {BCD} = \widehat {BCA} + \widehat {ACD} = 45^\circ + 30^\circ = 75^\circ $ Nên \(\widehat A = \widehat C = 75^\circ \) .
Câu 9 :
Cho tứ giác$ABCD$. Gọi $O$ là giao điểm của hai đường chéo $AC$ và$BD$ . Khẳng định nào sau đây là đúng nhất.
Đáp án : C Phương pháp giải :
Ta sử dụng : “ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.” Lời giải chi tiết :
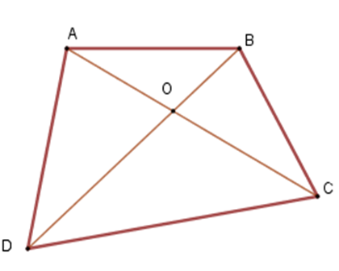 + Xét tam giác \(OAB\) ta có \(OA + OB > AB\)(vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) . Tương tự ta có \(OC + OD > CD;\,OB + OC > BC;\,OA + OD > AD\) Cộng vế với vế ta được \(OA + OB + OC + OD + OB + OC + OA + OD > AB + BC + CD + AD\) \( \Leftrightarrow 2\left( {OA + OB + OC + OD} \right) > AB + BC + CD + DA\) \( \Leftrightarrow OA + OB + OC +OD> \dfrac{{AB + BC + CD + DA}}{2}\) nên B đúng. + Xét tam giác \(ABC\) ta có \(AB + BC > AC\) (vì trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại) . Tương tự ta có \(BC + CD > BD;\,CD + DA > AC;\,AD + DB > BD\) Cộng vế với vế ta được: \(AB + BC + BC + CD + CD + DA + DA + AB > AC + BD + AC + BD\) \( \Leftrightarrow 2\left( {AB + BC + CD + DA} \right) > 2\left( {AC + BD} \right)\) \( \Leftrightarrow AB + BC + CD + DA > AC + BD\) mà \(AC + BD = OA + OC + OB + OD\) nên \(AB + BC + CD + DA > OA + OB + OC + OD\) nên A đúng. Vậy cả A, B đều đúng.
Câu 10 :
Cho tứ giác \(ABCD\) biết số đo của các góc \(\widehat A;\,\widehat B;\,\widehat C;\,\widehat D\) tỉ lệ thuận với $4;3;5;6.$ Khi đó số đo các góc \(\widehat A;\,\widehat B;\,\widehat C;\,\widehat D\) lần lượt là:
Đáp án : A Phương pháp giải :
Ta sử dụng tính chất tỉ lệ thức \(\dfrac{A}{B} = \dfrac{C}{D} = \dfrac{{A + C}}{{B + D}}\) và định lý về tổng các góc trong tứ giác bằng \(360^\circ \) . Lời giải chi tiết :
Vì số đo của các góc \(\widehat A;\,\widehat B;\,\widehat C;\,\widehat D\) tỉ lệ thuận với $4;3;5;6$ nên ta có \(\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{5} = \dfrac{{\widehat D}}{6} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{4 + 3 + 5 + 6}} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}}\) (tính chất dãy tỉ số bằng nhau) Mà \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \) nên ta có \(\dfrac{{\widehat A}}{4} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{5} = \dfrac{{\widehat D}}{6} = \dfrac{{\widehat A + \widehat B + \widehat C + \widehat D}}{{18}} = \dfrac{{360^\circ }}{{18}} = 20^\circ \) \( \Rightarrow \widehat A = 4.20^\circ = 80^\circ \) ; \(\widehat B = 3.20^\circ = 60^\circ ;\,\widehat C = 5.20^\circ = 100^\circ ;\,\widehat D = 6.20^\circ = 120^\circ \) Nên số đo góc \(\widehat A;\widehat B;\widehat C;\,\widehat D\) lần lượt là \(80^\circ ;\,60^\circ ;\,100^\circ ;\,120^\circ \) .
Câu 11 :
Tam giác \(ABC\) có \(\widehat A = 60^\circ \), các tia phân giác của góc \(B\) và \(C\) cắt nhau tại \(I.\) Các tia phân giác góc ngoài tại đỉnh \(B\) và \(C\) cắt nhau tại \(K\). Tính các góc \(\widehat {BIC};\,\widehat {BKC}.\)
Đáp án : D Phương pháp giải :
+ Sử dụng tính chất tia phân giác của một góc + Định lý: Tổng ba góc trong tam giác bằng \(180^\circ \) + Định lý: Tổng bốn góc trong tứ giác bằng \(360^\circ \) Lời giải chi tiết :
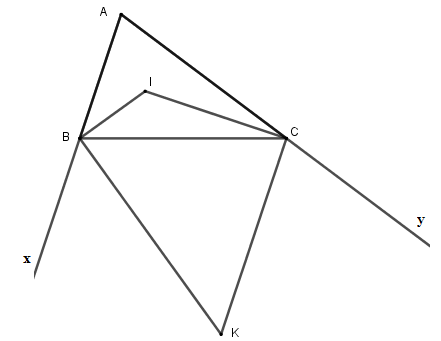 Xét tam giác \(ABC\) có: \(\widehat A + \widehat {ABC} + \widehat {BCA} = 180^\circ \Leftrightarrow \widehat {ABC} + \widehat {BCA} = 120^\circ \). Vì \(BI\) là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}\). Vì \(CI\) là phân giác \(\widehat {BCA} \Rightarrow \widehat {BCI} = \dfrac{1}{2}\widehat {BCA}\). Từ đó: \(\widehat {CBI} + \widehat {BCI} = \dfrac{1}{2}\left( {\widehat {BAC} + \widehat {BCA}} \right) = \dfrac{1}{2}.120^\circ = 60^\circ \). Xét tam giác \(BCI\) có: \(\widehat {BCI} + \widehat {BIC} + \widehat {CBI} = 180^\circ \) nên \(\widehat {BIC} = 180^\circ - \left( {\widehat {BCI} + \widehat {CBI}} \right) = 180^\circ - 60^\circ = 120^\circ \). Vì \(BI\) là phân giác \(\widehat {BAC} \Rightarrow \widehat {CBI} = \dfrac{1}{2}\widehat {BAC}\). Vì \(BK\) là phân giác \(\widehat {CBx} \Rightarrow \widehat {CKB} = \dfrac{1}{2}\widehat {CBx}\). Suy ra: \(\widehat {CBK} + \widehat {CBI} = \dfrac{1}{2}\left( {\widehat {CBx} + \widehat {ABC}} \right) = \dfrac{1}{2}.180^\circ = 90^\circ \) hay \(\widehat {IBK} = 90^\circ \). Tương tự ta có: \(\widehat {ICK} = 90^\circ \). Xét tứ giác \(BICK\) có: \(\widehat {BIC} + \widehat {IBC} + \widehat {ICK} + \widehat {BKC} = 360^\circ \)\( \Leftrightarrow \widehat {BKC} = 360^\circ - 90^\circ - 90^\circ - 120^\circ = 60^\circ \). Vậy \(\widehat {BIC} = 120^\circ ;\,\widehat {BKC} = 60^\circ .\)
Câu 12 :
Tứ giác \(ABCD\) có \(\widehat C + \widehat D = 90^\circ .\) Chọn câu đúng.
Đáp án : B Phương pháp giải :
+ Gọi giao điểm của \(AD\) và \(BC\) là \(K.\) + Sử dụng định lý Pytago. Lời giải chi tiết :
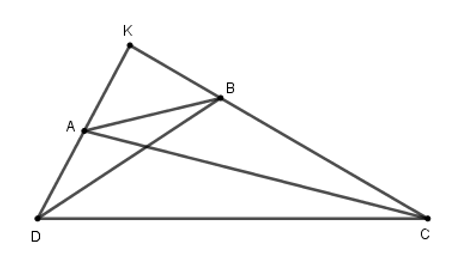 Gọi \(K\) là giao điểm \(AD,BC\). Vì \(\widehat C + \widehat D = 90^\circ \) nên \(\widehat K = 90^\circ \). Xét \(\Delta KAC\) vuông tại \(K\) ta có: \(A{C^2} = K{C^2} + K{A^2}\). Xét \(\Delta KBD\) vuông tại \(K\) có: \(B{D^2} = K{B^2} + K{D^2}\). Xét \(\Delta KBA\) vuông tại \(K\) có: \(B{A^2} = K{A^2} + K{B^2}\). Xét \(\Delta KCD\) vuông tại \(K\) có: \(C{D^2} = K{C^2} + K{D^2}\). Từ đó \(B{D^2} + A{C^2} = K{C^2} + K{A^2} + K{B^2} + K{D^2}\)\( = \left( {K{B^2} + K{A^2}} \right) + \left( {K{D^2} + K{C^2}} \right) = A{B^2} + D{C^2}\)
Câu 13 :
Tứ giác \(ABCD\) có \(\widehat A - \widehat C = 60^\circ .\) Các tia phân giác của các góc \(B\) và \(D\) cắt nhau tại \(I.\) Tính số đo góc \(BID.\)
Đáp án : A Phương pháp giải :
Sử dụng: Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó. Sử dụng: Tổng bốn góc trong tứ giác bằng \(360^\circ .\) Lời giải chi tiết :
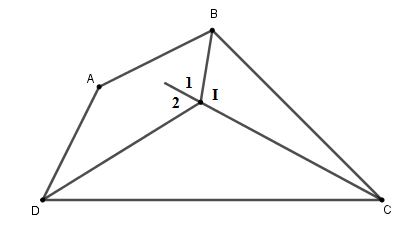 Xét tam giác \(BIC\) có: \(\widehat {IBC} = \widehat {{I_1}} - \widehat {BCI}\). Xét tam giác \(DIC\) có: \(\widehat {IDC} = \widehat {{I_2}} - \widehat {ICD}\). Nên \(\widehat {IBC} + \widehat {IDC} = \left( {\widehat {{I_1}} + \widehat {{I_2}}} \right) - \left( {\widehat {{C_1}} + \widehat {{C_2}}} \right)\)\( = \widehat {BID} - \widehat C\). Tứ giác \(ABID\) có: \(\widehat {ABI} + \widehat {ADI} = 360^\circ - \widehat A - \widehat {BID}\). Do \(\widehat {ABI} = \widehat {IBC};\,\widehat {ADI} = \widehat {IDC}\) (tính chất tia phân giác) nên \(\widehat {IBC} + \widehat {IDC} = \widehat {ABI} + \widehat {ADI}\). Hay \(\widehat {BID} - \widehat C = 360^\circ - \widehat A - \widehat {BID}\)\( \Leftrightarrow 2\widehat {BID} = 360^\circ - \left( {\widehat A - \widehat C} \right) = 360^\circ - 60^\circ = 300^\circ \). Suy ra \(\widehat {BID} = 150^\circ .\)
|
