Trắc nghiệm Bài tập ôn tập chương 5 Toán 8Đề bài
Câu 1 :
Một tứ giác là hình bình hành nếu nó là:
Câu 2 :
Hình bình hành có hai đường chéo vuông góc là:
Câu 3 :
Tứ giác có 2 cạnh đối song song và 2 đường chéo bằng nhau là:
Câu 4 :
Trong các tứ giác sau, tứ giác nào là hình có \(4\) trục đối xứng?
Câu 5 :
Một tam giác đều có độ dài cạnh bằng $14{\rm{ }}cm$ . Độ dài một đường trung bình của tam giác đó là:
Câu 6 :
Cho tứ giác $ABCD,$ có \(\widehat A = {70^0},\) \(\widehat B = {120^0},\) \(\widehat D = {50^0},\) Số đo \(\widehat C\) là:
Câu 7 :
Hình thang $ABCD$ ($AB\, // \, CD$ ) có số đo góc $D$ bằng ${70^0},$ số đo góc $A$ là:
Câu 8 :
Một hình thang cân có cạnh bên là $2,5cm;$ đường trung bình là $3\,cm.$ Chu vi của hình thang là:
Câu 9 :
Độ dài một cạnh hình vuông bằng $5\,cm.$ Thì độ dài đường chéo hình vuông đó sẽ là:
Câu 10 :
Hình thoi có độ dài hai đường chéo lần lượt bằng $12cm$ và $16cm.$ Độ dài cạnh hình thoi đó là:
Câu 11 :
Cho hình thang $ABCD\left( {AB//CD} \right),{\rm{ }}M$ là trung điểm của $AD,{\rm{ }}N$ là trung điểm của $BC.$ Gọi $I,{\rm{ }}K$ theo thứ tự là giao điểm của $MN$ với $BD,{\rm{ }}AC.$ Cho biết $AB = 6cm,{\rm{ }}CD = 14cm.$ Tính độ dài $MI,{\rm{ }}IK.$
Câu 12 :
Cho hình bình hành \(ABCD\) có $DC = 2BC$. Gọi $E,F$ là trung điểm của $AB,DC$. Gọi $AF$ cắt $DE$ tại $I,{\rm{ }}BF$ cắt $CE$ tại $K.$ Câu 12.1
Chọn câu đúng nhất.
Câu 12.2
Tứ giác $EIFK$ là hình gì?
Câu 12.3
Hình bình hành $ABCD$ có thêm điều kiện gì thì $EIFK$ là hình vuông ?
Câu 13 :
Cho tam giác $ABC$ cân tại $A,$ trung tuyến $AM.$ Gọi $I$ là trung điểm của $AC,{\rm{ }}K$ là điểm đối xứng với $M$ qua $I.$ Câu 13.1
Tứ giác $AMCK$ là hình gì?
Câu 13.2
Tứ giác $AKMB$ là hình gì?
Câu 13.3
Tìm điều kiện của tam giác $ABC$ để tứ giác $AMCK$ là hình vuông?
Câu 14 :
Cho hình bình hành $ABCD$ có $BC = 2AB\;$ và $\widehat A = 60^\circ $ . Gọi $E,F\;$ theo thứ tự là trung điểm của $BC$ và $AD.$ Gọi $I$ là điểm đối xứng với $A$ qua $B.$ Câu 14.1
Tứ giác $BICD$ là hình gì?
Câu 14.2
Số đo góc $AED$ là:
Câu 15 :
Cho tứ giác $ABCD.$ Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm các cạnh $AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA.$ Hai đường chéo $AC$ và $BD$ phải thỏa mãn điều kiện gì để $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ là bốn đỉnh của hình vuông.
Câu 16 :
Cho tam giác $ABC.$ Gọi $D,E,F\;$ theo thứ tự là trung điểm của $AB,BC,CA.$ Gọi $M,N,P,Q$ theo thứ tự là trung điểm của $AD,AF,EF,ED.\;$ $\Delta ABC$ có điều kiện gì thì $MNPQ$ là hình chữ nhật?
Câu 17 :
Cho tam giác $ABC$ \(\left( {\widehat {A\,\,} < {{90}^0}} \right)\). Về phía ngoài của tam giác $ABC$ dựng các hình vuông $ABDE,{\rm{ }}ACFG.$ Gọi $M$ là trung điểm của đoạn thẳng $DF.$ Chọn câu đúng.
Câu 18 :
Cho hình vuông $ABCD,{\rm{ }}E$ là một điểm trên cạnh $CD.$ Tia phân giác của góc $BAE$ cắt $BC$ tại $M.$ Chọn câu đúng.
Lời giải và đáp án
Câu 1 :
Một tứ giác là hình bình hành nếu nó là:
Đáp án : B Lời giải chi tiết :
+ Đáp án A là hình thang cân. + Đáp án C là hình thang cân. + Đáp án D chưa đủ điều kiện để là hình bình hành. + Dựa vào dấu hiệu nhận biết hình bình hành ta thấy một tứ giác là hình bình hành nếu có hai cạnh đối song song và bằng nhau nên đáp án B đúng.
Câu 2 :
Hình bình hành có hai đường chéo vuông góc là:
Đáp án : B Lời giải chi tiết :
Theo dấu hiệu nhận biết hình thoi thì hình bình hành có hai đường chéo vuông góc là hình thoi.
Câu 3 :
Tứ giác có 2 cạnh đối song song và 2 đường chéo bằng nhau là:
Đáp án : B Lời giải chi tiết :
Tứ giác có 2 cạnh đối song song là hình thang. Lại thêm có 2 đường chéo bằng nhau nên tứ giác đó là hình thang cân.
Câu 4 :
Trong các tứ giác sau, tứ giác nào là hình có \(4\) trục đối xứng?
Đáp án : B Phương pháp giải :
+ Dựa vào tính chất của các hình để suy ra trục đối xứng Lời giải chi tiết :
+) Hình vuông là tứ giác có 4 trục đối xứng. +) Hình chữ nhật có 2 trục đối xứng là hai đường trung trực của các cạnh. +) Hình bình hành không có trục đối xứng. +) Hình thoi có 2 trục đối xứng là 2 đường chéo.
Câu 5 :
Một tam giác đều có độ dài cạnh bằng $14{\rm{ }}cm$ . Độ dài một đường trung bình của tam giác đó là:
Đáp án : B Phương pháp giải :
Dựa vào tính chất: đường trung bình của tam giác bằng một nửa cạnh đáy. Lời giải chi tiết :
Độ dài một đường trung bình của tam giác là: \(14:2 = 7\,cm.\)
Câu 6 :
Cho tứ giác $ABCD,$ có \(\widehat A = {70^0},\) \(\widehat B = {120^0},\) \(\widehat D = {50^0},\) Số đo \(\widehat C\) là:
Đáp án : C Phương pháp giải :
Dựa vào tính chất tổng các góc của một tứ giác bằng \({360^0}\). Lời giải chi tiết :
Xét tứ giác \(ABCD\) ta có: $\hat A + \widehat B + \widehat C + \widehat D = {360^0}$ $\begin{array}{l} \Rightarrow \widehat C = {360^0} - \left( {\hat A + \widehat B + \widehat D} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - \left( {{{70}^0} + {{120}^0} + {{50}^0}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {240^0} = {120^0}.\end{array}$
Câu 7 :
Hình thang $ABCD$ ($AB\, // \, CD$ ) có số đo góc $D$ bằng ${70^0},$ số đo góc $A$ là:
Đáp án : C Phương pháp giải :
Ta sử dụng tính chất của hình thang: Ta thấy góc $A$ và $D$ là hai góc trong cùng phía nên \(\widehat A + \widehat D = {180^0}\) từ đó ta suy ra số đo góc $A.$ Lời giải chi tiết :
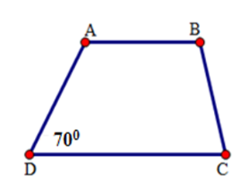 Ta có: \(\widehat A + \widehat D = {180^0}\) \(\begin{array}{l} \Rightarrow \widehat A = {180^0} - \widehat D\\\,\,\,\,\,\,\,\,\,\,\,\, = {180^0} - {70^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = {110^0}\end{array}\)
Câu 8 :
Một hình thang cân có cạnh bên là $2,5cm;$ đường trung bình là $3\,cm.$ Chu vi của hình thang là:
Đáp án : D Phương pháp giải :
+ Dựa vào tính chất của hình thang cân suy ra hai cạnh bên bằng nhau và bằng 2,5cm. + Tổng độ dài hai đáy bằng hai lần độ dài đường trung bình + Tổng độ dài hai đáy và độ dài hai cạnh bên là chu vi hình thang cân cần tìm. Lời giải chi tiết :
Tổng độ dài hai đáy là: \(3.2 = 6(cm)\) Chu vi hình thang là: \(2,5.2 + 6 = 11(cm)\)
Câu 9 :
Độ dài một cạnh hình vuông bằng $5\,cm.$ Thì độ dài đường chéo hình vuông đó sẽ là:
Đáp án : B Phương pháp giải :
Áp dụng định lý Py-ta-go để tính độ dài đường chéo hình vuông. Lời giải chi tiết :
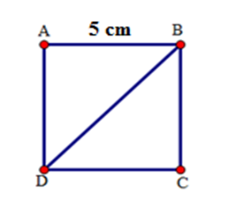 Cho hình vuông $ABCD$ có cạnh bằng $5cm.$ Xét tam giác $ABD$ vuông tại $A,$ theo định lý Pytago ta có: \(\begin{array}{l}B{D^2} = A{B^2} + A{D^2} = {5^2} + {5^2} = 50\\ \Rightarrow BD = \sqrt {50} = 5\sqrt 2 (cm)\end{array}\)
Câu 10 :
Hình thoi có độ dài hai đường chéo lần lượt bằng $12cm$ và $16cm.$ Độ dài cạnh hình thoi đó là:
Đáp án : D Phương pháp giải :
+ Dựa vào tính chất của hình thoi để suy ra hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường. + Sử dụng định lý Pytago để tính độ dài cạnh hình thoi. Lời giải chi tiết :
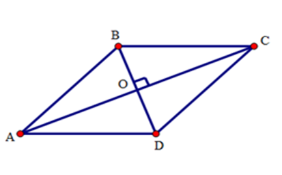
Giả sử hình thoi $ABCD$ có hai đường chéo $AC = 16cm,{\rm{ }}BD = 12cm$ cắt nhau tại $O.$ Theo tính chất hình thoi ta có $AC$ vuông góc với $BD,{\rm{ }}O$ là trung điểm của $AC,{\rm{ }}BD.$ Do đó: \(OA = \dfrac{1}{2}AC = 16:2 = 8(cm);\,\,\,OB = \dfrac{1}{2}BD = 12:2 = 6(cm)\) Áp dụng định lý Pytago cho tam giác $ABO$ vuông tại $O$ ta có: \(A{B^2} = O{A^2} + O{B^2} = {6^2} + {8^2} = 100 \Rightarrow AB = 10(cm)\) Vậy độ dài cạnh hình thoi là $10\,cm.$
Câu 11 :
Cho hình thang $ABCD\left( {AB//CD} \right),{\rm{ }}M$ là trung điểm của $AD,{\rm{ }}N$ là trung điểm của $BC.$ Gọi $I,{\rm{ }}K$ theo thứ tự là giao điểm của $MN$ với $BD,{\rm{ }}AC.$ Cho biết $AB = 6cm,{\rm{ }}CD = 14cm.$ Tính độ dài $MI,{\rm{ }}IK.$
Đáp án : D Phương pháp giải :
+ Dựa vào tính chất đường trung bình của tam giác để tính độ dài $MI,{\rm{ }}MK.$ Từ đó suy ra độ dài $IK.$ Lời giải chi tiết :
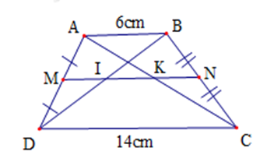 - Hình thang $ABCD$ có: $\left. \begin{array}{l}{\rm{AM}} = {\rm{MD(gt)}}\\{\rm{BN}} = {\rm{NC (gt)}}\end{array} \right\} \Rightarrow $$MN$ là đường trung bình của hình thang $ABCD.$ \( \Rightarrow \) $MN//AB//CD$ (tính chất). - Tam giác $ABD$ có: $\left. \begin{array}{l}{\rm{AM }} = {\rm{ MD}}\\MI//AB\end{array} \right\} \Rightarrow $$ID = IB$ (định lý đảo về đường trung bình của tam giác). \( \Rightarrow \) $MI$ là đường trung bình của $\Delta ADB$ $ \Rightarrow MI = \dfrac{1}{2}AB = \dfrac{1}{2}.6 = 3(cm)$ - Tương tự tam giác \(ACD\) có: $AM = MD,{\rm{ }}MK//DC$ nên $AK = KC,$ hay ${\rm{ }}MK$ là đường trung bình của tam giác $ACD$, ta có: $MK = \dfrac{1}{2}CD = \dfrac{1}{2}.14 = 7(cm)$ \( \Rightarrow \) $IK = MK - MI = 7 - 3 = 4\left( {cm} \right)$ Vậy \(MI = 3cm;IK = 4cm.\)
Câu 12 :
Cho hình bình hành \(ABCD\) có $DC = 2BC$. Gọi $E,F$ là trung điểm của $AB,DC$. Gọi $AF$ cắt $DE$ tại $I,{\rm{ }}BF$ cắt $CE$ tại $K.$ Câu 12.1
Chọn câu đúng nhất.
Đáp án : D Phương pháp giải :
+ Chỉ ra các cặp cạnh song song và bằng nhau + Sử dụng các dấu hiệu nhận biết hình bình hành, hình thoi, hình vuông Lời giải chi tiết :
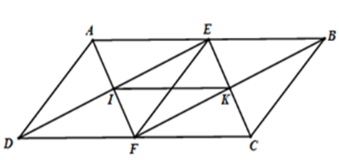 Xét hình bình hành \(ABCD\) có \(E;F\) lần lượt là trung điểm của \(AB;CD\); \(DC = 2BC\) nên \(AE = EB = BC = CF = DF = AD\) ;\(AB//CD;\,AD//BC\) Xét tứ giác \(DEBF\) có \(\left\{ \begin{array}{l}EB//DF\\EB = DF\end{array} \right.\) nên \(DEBF\) là hình bình hành (dhnb) Xét tứ giác \(AEFD\) có \(AE = DF;AE//DF\) nên \(AEFD\) là hình bình hành (dhnb), lại có \(AE = AD\) nên hình bình hành \(AEFD\) là hình thoi. Tương tự ta cũng có \(EBCF\) là hình thoi. Nhận thấy chưa đủ điều kiện để \(EBCF\) là hình vuông. Nên A, B đúng, C sai. Câu 12.2
Tứ giác $EIFK$ là hình gì?
Đáp án : A Phương pháp giải :
Chứng minh $EIFK$ là hình bình hành dựa vào dấu hiệu tứ giác có cặp cạnh đối song song và bằng nhau. Tìm thêm tính chất của hình bình hành $EIFK$ để sử dụng dấu hiệu hình bình hành có một góc vuông. Lời giải chi tiết :
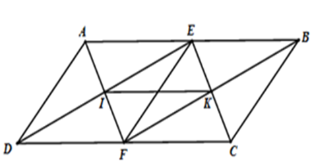 Theo câu trước ta có tứ giác \(BEDF\) là hình bình hành nên \(ED = BF;\,ED//BF \Rightarrow EI//FK\,\left( 1 \right)\) Theo câu trước ta có tứ giác \(AEDF\) và \(BEFC\) là hình thoi nên \(I;K\) lần lượt là trung điểm của \(DE\) và \(BF\) Suy ra \(EI = \dfrac{{DE}}{2};\,FK = \dfrac{{BF}}{2}\) mà \(DE = BF\left( {cmt} \right) \Rightarrow EI = FK\,\,\left( 2 \right)\) Từ (1) và (2) suy ra tứ giác \(EIFK\) là hình bình hành. Mà \(AEDF\) là hình thoi nên \(AF \bot DE\) (tính chất hình thoi)\( \Rightarrow \widehat {EIF} = 90^\circ \) Hình bình hành \(EIFK\) có một góc vuông \(\widehat {EIF} = 90^\circ \) nên \(EIFK\) là hình chữ nhật. Câu 12.3
Hình bình hành $ABCD$ có thêm điều kiện gì thì $EIFK$ là hình vuông ?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông để suy ra điều kiện của hình bình hành \(ABCD.\) Lời giải chi tiết :
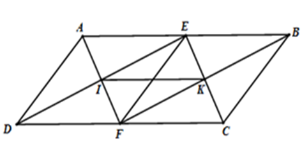 Ta có $EIFK$ là hình chữ nhật (theo câu trước). Để hình chữ nhật $EIFK$ là hình vuông $ \Leftrightarrow IE = {\rm{IF}}\left( 1 \right)$. Mà \(I\) là giao điểm hai đường chéo \(DE;AF\) của hình thoi\(AEFD\) nên $IE = \dfrac{1}{2}DE;{\rm{IF = }}\dfrac{1}{2}{\rm{AF}} \Rightarrow {\rm{DE = AF}}$ Mặt khác ta có $AEFD$ là hình thoi (chứng minh ở câu trước) (2). Từ (1) và (2) $ \Rightarrow AEFD$ là hình vuông $ \Rightarrow AD \bot DC$. Suy ra hình bình hành \(ABCD\) phải là hình chữ nhật thì \(EIFK\) là hình vuông.
Câu 13 :
Cho tam giác $ABC$ cân tại $A,$ trung tuyến $AM.$ Gọi $I$ là trung điểm của $AC,{\rm{ }}K$ là điểm đối xứng với $M$ qua $I.$ Câu 13.1
Tứ giác $AMCK$ là hình gì?
Đáp án : A Phương pháp giải :
+ Chứng minh $AKCM$ là hình bình hành dựa vào dấu hiệu hai đường chéo giao nhau tại trung điểm mỗi đường + Tìm thêm tính chất của \(AKCM\) để sử dụng dấu hiệu hình bình hành có một góc vuông. Lời giải chi tiết :
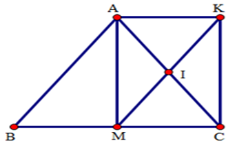 \(\Delta ABC\) cân tại $A$ có $AM$ là trung tuyến nên $AM$ đồng thời là đường cao\( \Rightarrow AM \bot BC \Rightarrow \widehat {AMC} = {90^0}.\) (1) Xét tứ giác $AMCK$ có: $AC$ cắt $MK$ tại $I,$ mà $AI = IC,MI = IK\;$ (gt) \( \Rightarrow \) Tứ giác $AMCK$ là hình bình hành (dấu hiệu nhận biết) (2) Từ (1) và (2) \( \Rightarrow \) $AMCK$ là hình chữ nhật (dấu hiệu nhận biết). Câu 13.2
Tứ giác $AKMB$ là hình gì?
Đáp án : D Phương pháp giải :
Dựa vào dấu hiệu tứ giác có một cặp cạnh song song và bằng nhau. Lời giải chi tiết :
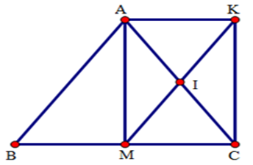 Tứ giác $AMCK$ là hình chữ nhật (theo câu trước) \( \Rightarrow \) $AK//CM$ \( \Rightarrow \)$AK//BM$ (3) mà $AK = MC{\rm{ }}(AMCK$ là hình chữ nhật) và $MC = MB$ (gt) \( \Rightarrow \)$AK = BM$ (4) Từ (3) và (4) \( \Rightarrow \)Tứ giác $AKMB$ là hình bình hành. (dấu hiệu nhận biết) Câu 13.3
Tìm điều kiện của tam giác $ABC$ để tứ giác $AMCK$ là hình vuông?
Đáp án : C Phương pháp giải :
+ Để $AMCK$ là hình vuông ta dựa vào dấu hiệu hình chữ nhật có hai cạnh bên bằng nhau là hình vuông, từ đó suy ra điều kiện của tam giác $ABC.$ Lời giải chi tiết :
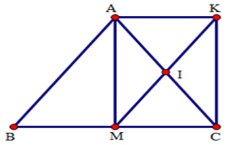 Theo câu trước thì \(AKCM\) là hình chữ nhật. Để hình chữ nhật $AMCK$ là hình vuông thì $AM = MC$ Mà $AM$ là đường trung tuyến của tam giác cân $ABC$ \( \Rightarrow AM = MC = \dfrac{1}{2}BC \Rightarrow \) Tam giác $ABC$ vuông cân tại $A.$
Câu 14 :
Cho hình bình hành $ABCD$ có $BC = 2AB\;$ và $\widehat A = 60^\circ $ . Gọi $E,F\;$ theo thứ tự là trung điểm của $BC$ và $AD.$ Gọi $I$ là điểm đối xứng với $A$ qua $B.$ Câu 14.1
Tứ giác $BICD$ là hình gì?
Đáp án : A Phương pháp giải :
+ Chứng minh \(BICD\) là hình bình hành + Tìm thêm tính chất của \(BICD\) để sử dụng dấu hiệu hình bình hành có một góc vuông Lời giải chi tiết :
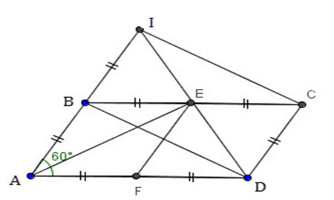 Do $AB//CD$ (giả thiết) nên $BI//CD$ Theo giả thiết ta có \(BI = AB = AF = FD \Rightarrow AI = AD\) mà \(\widehat {IAD} = 60^\circ \) (gt) nên tam giác \(ADI\) đều. Câu 14.2
Số đo góc $AED$ là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất hình chữ nhật Sử dụng tính chất tam giác đều Lời giải chi tiết :
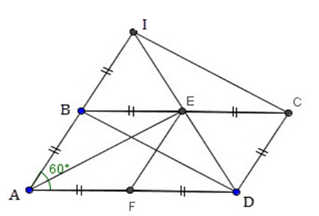 Theo câu trước ta có \(BICD\) là hình chữ nhật lại có \(E\) là trung điểm của \(BC\) (gt) nên \(E\) cũng là trung điểm của \(ID.\) Mà tam giác \(ADI\) đều (theo câu trước) có \(AE\) là đường trung tuyến nên \(AE\) cũng là đường cao, suy ra \(AE \bot BD \Rightarrow \widehat {AED} = 90^\circ .\)
Câu 15 :
Cho tứ giác $ABCD.$ Gọi $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ lần lượt là trung điểm các cạnh $AB,{\rm{ }}BC,{\rm{ }}CD,{\rm{ }}DA.$ Hai đường chéo $AC$ và $BD$ phải thỏa mãn điều kiện gì để $M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q$ là bốn đỉnh của hình vuông.
Đáp án : D Phương pháp giải :
Chứng minh \(MNPQ\) là hình bình hành Dựa vào dấu hiệu nhận biết hình vuông để tìm ra điều kiện của hai đường chéo $AC$ và $BD$ tương ứng. Lời giải chi tiết :
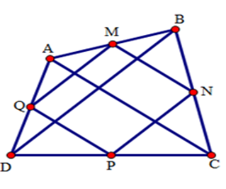 Xét tam giác $ABD$ có: $M$ là trung điểm của $AB$ (gt) $Q$ là trung điểm của $AD$ (gt) \( \Rightarrow \) $QM$ là đường trung bình của tam giác $ABD.$ (định lý) Do đó $QM//BD$ và \(QM = \dfrac{1}{2}BD\) (1) Tương tự ta cũng có $NP$ là đường trung bình của tam giác $BCD.$ \( \Rightarrow \left\{ \begin{array}{l}NP//BD\\NP = \dfrac{1}{2}BD\,\,\,\,\left( 2 \right)\end{array} \right.\) Từ (1) và (2) ta suy ra $MNPQ$ là hình bình hành (dấu hiệu nhận biết). Tương tự ta cũng có $MN$ là đường trung bình của tam giác $BAC$ nên $MN//AC$ và \(MN = \dfrac{1}{2}AC\) Để hình bình hành $MNPQ$ là hình vuông \( \Leftrightarrow \left\{ \begin{array}{l}MN \bot NP\\MN = NP\end{array} \right.\) + Để \(MN \bot NP \Leftrightarrow AC \bot BD\) (vì $MN//AC,{\rm{ }}NP//BD$ ) + Để \(MN = NP \Leftrightarrow AC = BD\) (vì \(MN = \dfrac{1}{2}AC,NP = \dfrac{1}{2}BD\) ) Vậy điều kiện cần tìm để $MNPQ$ là hình vuông là \(BD = AC;BD \bot AC.\) .
Câu 16 :
Cho tam giác $ABC.$ Gọi $D,E,F\;$ theo thứ tự là trung điểm của $AB,BC,CA.$ Gọi $M,N,P,Q$ theo thứ tự là trung điểm của $AD,AF,EF,ED.\;$ $\Delta ABC$ có điều kiện gì thì $MNPQ$ là hình chữ nhật?
Đáp án : A Phương pháp giải :
Chứng minh \(MNPQ\) là hình bình hành Dựa vào dấu hiệu nhận biết hình chữ nhật để suy ra điều kiện của tam giác \(ABC.\) Lời giải chi tiết :
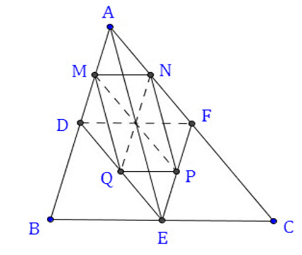 Xét $\Delta ADE$ có: $AM = DM;DQ = EQ$ nên $MQ$ là đường trung bình của $\Delta ADE$ . Suy ra $MQ//NP $ ( cùng $//AE$ ) và $MQ = NP(= \dfrac{1}{2}AE)$ Để $MNPQ$ là hình chữ nhật thì $MN \bot NP$ (1) Vậy $MN//BC$ (3) Từ (1), (2), (3) suy ra: $AE \bot BC$ .
Câu 17 :
Cho tam giác $ABC$ \(\left( {\widehat {A\,\,} < {{90}^0}} \right)\). Về phía ngoài của tam giác $ABC$ dựng các hình vuông $ABDE,{\rm{ }}ACFG.$ Gọi $M$ là trung điểm của đoạn thẳng $DF.$ Chọn câu đúng.
Đáp án : A Phương pháp giải :
+ Vẽ thêm điểm $H$ sao cho tam giác $BHC$ vuông cân đỉnh $B,{\rm{ }}H$ thuộc nửa mặt phẳng bờ $BC$ có chứa điểm $A.$ + Chứng minh $M$ là trung điểm của $HC$ + Chứng minh $MB$ vuông góc với $MC$ để suy ra tính chất tam giác \(MBC\) . Lời giải chi tiết :
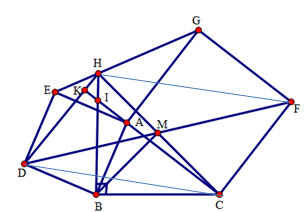 Trên nửa mặt phẳng bờ $BC$ có chứa $A$ dựng tam giác $BHC$ vuông cân đỉnh $B.$ Xét tam giác $BHD$ và tam giác $BCA$ có: $DB = BA$ (Vì $ADBE$ là hình vuông) \(\widehat {DBH} = \widehat {ABC}\) (vì cùng phụ với góc $HBA$ ) $BH = BC$ (vì tam giác $BHC$ vuông cân đỉnh $B$ ) Do đó: \(\Delta BHD = \Delta BCA\,\,(c.g.c)\), suy ra \(DH = AC,\widehat {BHD} = \widehat {BCA}\). $AC$ cắt $HD$ tại $K,$ cắt $BH$ tại $I.$ Xét tam giác $IHK$ và tam giác $ICB$ có: \(\widehat {HIK} = \widehat {CIB}\) (đối đỉnh), \(\widehat {BHD} = \widehat {BCA}\), do đó \(\widehat {HKI} = \widehat {IBC} = {90^0} \Rightarrow KC \bot DH\) Mặt khác \(KC \bot CF\), do đó $DH//CF$ . Ta có $DH = CF{\rm{ }}\left( { = AC} \right)$ và $DH//CF$ nên $DHFC$ là hình bình hành. Mà $M$ là trung điểm của $DF$ nên $M$ là trung điểm của $HC,$ suy ra tam giác $MBC$ vuông cân đỉnh $M.$
Câu 18 :
Cho hình vuông $ABCD,{\rm{ }}E$ là một điểm trên cạnh $CD.$ Tia phân giác của góc $BAE$ cắt $BC$ tại $M.$ Chọn câu đúng.
Đáp án : C Phương pháp giải :
Vẽ $EF \bot AM(F \in AB)$ Chứng minh $EF = AM.$ Chứng minh tam giác $AEF$ cân đỉnh$A.$ Chỉ ra $ME = MF.$ Xét ba điểm $M,{\rm{ }}E,{\rm{ }}F$ ta có: \(EF \le ME + MF\) để suy ra hệ thức đúng. Lời giải chi tiết :
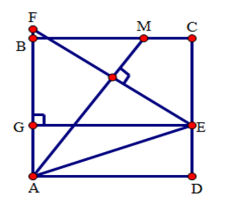 Vẽ $EF \bot AM(F \in AB),EG \bot AB(G \in AB)$. Tứ giác $AGED$ là hình chữ nhật( vì \(\widehat G = \widehat A = \widehat D = {90^0}\) ), suy ra $GE = AD.$ Lại thấy \(\widehat {FEG} = \widehat {MAB}\) (vì cùng phụ với \(\widehat {AFE}\) ) Xét \(\Delta GEF\) và \(\Delta BAM\)có: \(\widehat {EGF} = \widehat {ABM} = {90^0}\); $GE = AB{\rm{ }}\left( { = CD} \right);$\(\widehat {FEG} = \widehat {MAB}\) Do đó \(\Delta GEF = \Delta BAM\)(g.c.g) suy ra $EF = AM.$ Tam giác $AEF$ có $AM$ là đường phân giác và là đường cao nên tam giác $AEF$ cân đỉnh $A.$ Ta có $AM$ là đường trung trực của $EF,$ nên $ME = MF.$ Xét ba điểm $M,{\rm{ }}E,{\rm{ }}F$ ta có: \(EF \le ME + MF \Leftrightarrow EF \le 2ME\). Do đó \(AM \le 2ME\).
|
