Trắc nghiệm Bài tập ôn tập chương 4 Toán 8Đề bài
Câu 1 :
Cho các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn
Câu 2 :
Giá trị $x = 2$ là nghiệm của bất phương trình nào sau đây ?
Câu 3 :
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
Câu 4 :
Cho $a > b$. Bất đẳng thức nào tương đương với bất đẳng thức đã cho?
Câu 5 :
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
Câu 6 :
Phương trình \(\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\) có nghiệm là
Câu 7 :
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào? 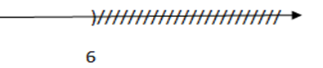
Câu 8 :
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
Câu 9 :
Tập nghiệm của bất phương trình $3x + 7 > x + 9$ là
Câu 10 :
Phương trình \(\left| {5x - 4} \right| = \left| {x + 2} \right|\) có nghiệm là
Câu 11 :
Tổng các nghiệm của phương trình \(7,5 - 3\left| {5 - 2x} \right| = - 4,5\) là
Câu 12 :
Số nghiệm của phương trình \(\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\) là
Câu 13 :
Hình vẽ nào dưới đây biểu diễn tập nghiệm của bất phương trình $2x - 8 \le 13 - 5x.$
Câu 14 :
Nghiệm của phương trình \(\left| {x - 1} \right| = 3x - 2\) là:
Câu 15 :
Số nguyên lớn nhất thỏa mãn bất phương trình ${(x - 2)^2} - {x^2} - 8x + 3 \ge 0$ là
Câu 16 :
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
Câu 17 :
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
Câu 18 :
Bất phương trình $2(x - 1) - x > 3(x - 1) - 2x - 5$ có nghiệm là:
Câu 19 :
Tập nghiệm của bất phương trình \(\dfrac{{x - 3}}{{x + 4}} < 0\) là
Câu 20 :
Tìm giá trị của x để biểu thức $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$ có giá trị dương
Câu 21 :
Phương trình \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\) có số nghiệm là
Câu 22 :
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
Câu 23 :
Tập nghiệm của các bất phương trình ${x^2} + 2(x - 3) - 1 > x(x + 5) + 5$ và $\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}$ lần lượt là
Câu 24 :
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
Câu 25 :
Chọn câu đúng, biết \(0 < a < b.\)
Câu 26 :
Cho số thực \(x\) , chọn câu đúng nhất.
Câu 27 :
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
Lời giải và đáp án
Câu 1 :
Cho các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn
Đáp án : A Phương pháp giải :
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn. Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn. Lời giải chi tiết :
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn ta có: Đáp án A là bất phương trình bậc nhất một ẩn. Đáp án B không phải bất phương trình bậc nhất một ẩn vì $a = 0.$ Đáp án C không phải bất phương trình bậc vì có \({x^2}.\) Đáp án D không phải bất phương trình vì đây là phương trình bậc nhất một ẩn.
Câu 2 :
Giá trị $x = 2$ là nghiệm của bất phương trình nào sau đây ?
Đáp án : D Phương pháp giải :
Có 2 cách làm: Cách 1: Giải từng bất phương trình tìm nghiệm rồi xem $x = 2$ có thỏa mãn không? Cách 2: Thay \(x = 2\) vào bất phương trình rồi so sánh hai vế của từng bất phương trình và kết luận Trong bài này các em nên sử dụng cách thứ 2 để cho nhanh gọn hơn đỡ tốn thời gian làm bài. Lời giải chi tiết :
(Trong bài này chúng ta làm theo cách thứ 2) thay \(x = 2\) vào từng bất phương trình: Đáp án A: \(7 - 2 < 2.2 \Leftrightarrow 5 < 4\) vô lý. Loại đáp án A. Đáp án B: \(2.2 + 3 > 9 \Leftrightarrow 7 > 9\) vô lý. Loại đáp án B. Đáp án C: \( - 4.2 \ge 2 + 5 \Leftrightarrow - 8 \ge 7\) vô lý. Loại đáp án C. Đáp án D: \(5 - 2 > 6.2 - 12 \Leftrightarrow 3 > 0\) luôn đúng. Chọn đáp án D.
Câu 3 :
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
Đáp án : D Phương pháp giải :
Giải bất phương trình tìm nghiệm phù hợp bằng cách dùng qui tắc nhân và qui tắc chuyển vế Lời giải chi tiết :
Vì \(7 > 0\) nên \(7\left( {3x + 5} \right) \ge 3 \Leftrightarrow 3x + 5 > 0 \Leftrightarrow 3x > - 5 \Leftrightarrow x > - \dfrac{5}{3}.\) Chú ý
Chuyển vế phải đổi dấu, chia cho một số dương thì bất phương trình không đổi chiều
Câu 4 :
Cho $a > b$. Bất đẳng thức nào tương đương với bất đẳng thức đã cho?
Đáp án : A Phương pháp giải :
Áp dụng tính chất liên hệ giữa thứ tự và phép cộng, liên hệ giữa thứ tự và phép nhân. Lời giải chi tiết :
+) Đáp án A: \(a > b \Leftrightarrow a - 3 > b - 3\) Vậy ý A đúng chọn luôn ý A. +) Đáp án B: \( - 3a + 4 > - 3b + 4 \Leftrightarrow - 3a > - 3b \Leftrightarrow a < b\) trái với giả thiết nên B sai. +) Đáp án C: \(2a + 3 < 2b + 3 \Leftrightarrow 2a < 2b \Leftrightarrow a < b\) trái với giả thiết nên C sai. +) Đáp án D: \( - 5b - 1 < - 5a - 1 \Leftrightarrow - 5b < - 5a \Leftrightarrow b > a\) trái với giả thiết nên D sai.
Câu 5 :
Phương trình \(\left| {2x - 5} \right| = 1\) có nghiệm là:
Đáp án : A Phương pháp giải :
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) Lời giải chi tiết :
Giải phương trình: \(\left| {2x - 5} \right| = 1\) $TH1:\;2x - 5 \ge 0 \Leftrightarrow x \ge \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = 2x - 5 = 1 \Leftrightarrow 2x = 6 \Leftrightarrow x = 3\;\;\left( {tm} \right)$ $TH2:\;2x - 5 < 0 \Leftrightarrow x < \dfrac{5}{2} \Rightarrow \left| {2x - 5} \right| = - 2x + 5 = 1 \Leftrightarrow 2x = 4 \Leftrightarrow x = 2\;\;\left( {tm} \right)$ Vậy phương trình có hai nghiệm \(x = 3\) và \(\;x = 2\). Chú ý
Khi chuyển vế phải đổi dấu.
Câu 6 :
Phương trình \(\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\) có nghiệm là
Đáp án : C Phương pháp giải :
Bỏ dấu giá trị tuyệt đối bằng công thức: \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) Lời giải chi tiết :
\(\begin{array}{l}\;\;\;\;\;\dfrac{1}{3} - \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{3} - \dfrac{1}{4}\\ \Leftrightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{1}{{12}}\,\left( * \right)\end{array}\) \(\begin{array}{l}TH1:\;\dfrac{5}{4} - 2x \ge 0 \Leftrightarrow x \le \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = \dfrac{5}{4} - 2x\\ \Rightarrow pt\,\,\left( * \right) \Leftrightarrow \dfrac{5}{4} - 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{7}{6}\\ \Leftrightarrow x = \dfrac{7}{{12}}\;\;\left( {tm} \right)\end{array}\) \(\begin{array}{l}TH2:\;\;\dfrac{5}{4} - 2x < 0 \Leftrightarrow x > \dfrac{5}{8} \Rightarrow \left| {\dfrac{5}{4} - 2x} \right| = - \dfrac{5}{4} + 2x\;\\ \Rightarrow pt\,\left( * \right) \Leftrightarrow - \dfrac{5}{4} + 2x = \dfrac{1}{{12}}\\ \Leftrightarrow 2x = \dfrac{4}{3}\\ \Leftrightarrow x = \dfrac{2}{3}\;\;\left( {tm} \right).\;\end{array}\) Vậy phương trình có hai nghiệm \(x = \dfrac{7}{{12}}\) và \(x = \dfrac{2}{3}\).
Câu 7 :
Hình vẽ dưới đây là biểu diễn tập nghiệm của bất phương trình nào? 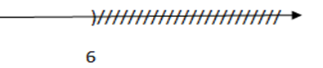
Đáp án : C Phương pháp giải :
Tìm nghiệm của mỗi phương trình rồi so sánh với đề bài. Lời giải chi tiết :
Theo đề bài thì trục số biểu diễn tập nghiệm \(x < 6.\) Ta có +) Đáp án A: $x - 1 \ge 5 \Leftrightarrow x \ge 6$ loại vì tập nghiệm là \(x < 6.\) +) Đáp án B: \(x + 1 \le 7 \Leftrightarrow x \le 6\) loại vì tập nghiệm là \(x < 6.\) +) Đáp án C: \(x + 3 < 9 \Leftrightarrow x < 6\) thỏa mãn vì tập nghiệm là \(x < 6.\) +) Đáp án D: \(x + 1 > 7 \Leftrightarrow x > 6\) loại vì tập nghiệm là \(x < 6.\)
Câu 8 :
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
Đáp án : C Phương pháp giải :
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn. Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn. Lời giải chi tiết :
Ta có: $m(2x + 1) < 8 \Leftrightarrow 2mx + m < 8 \Leftrightarrow 2mx + m - 8 < 0$. Vậy để bất phương trình \(m\left( {2x + 1} \right) < 8\) là bất phương trình bậc nhất 1 ẩn thì \(2mx + m - 8 < 0\) là bất phương trình bậc nhất một ẩn. Theo định nghĩa bất phương trình bậc nhất một ẩn thì \(a \ne 0\) hay \(2m \ne 0\) $\Leftrightarrow m \ne 0$
Câu 9 :
Tập nghiệm của bất phương trình $3x + 7 > x + 9$ là
Đáp án : A Phương pháp giải :
Áp dụng quy tắc chuyển vế để tìm nghiệm và biểu diễn trên trục số Lời giải chi tiết :
\(3x + 7 > x + 9 \Leftrightarrow 3x - x > 9 - 7 \Leftrightarrow 2x > 2 \Leftrightarrow x >1\) Vậy tập nghiệm của bất phương trình là $S = \left\{ {x|x > 1} \right\}$
Câu 10 :
Phương trình \(\left| {5x - 4} \right| = \left| {x + 2} \right|\) có nghiệm là
Đáp án : D Phương pháp giải :
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\) Ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\) Lời giải chi tiết :
$\begin{array}{l}\;\;\;\;\left| {5x - 4} \right| = \left| {x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}5x - 4 = x + 2\\5x - 4 = - x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}4x = 6\\6x = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{6}{4} = 1,5\\x = \dfrac{2}{6} = \dfrac{1}{3}\end{array} \right..\end{array}$
Câu 11 :
Tổng các nghiệm của phương trình \(7,5 - 3\left| {5 - 2x} \right| = - 4,5\) là
Đáp án : C Phương pháp giải :
Dùng qui tắc chuyển vế biến đổi phương trình về dạng \(\left| A \right| = m\,\,\left( {m \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = m\\A = - m\end{array} \right.\) Lời giải chi tiết :
\(\begin{array}{l}\;7,5 - 3\left| {5 - 2x} \right| = - 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 7,5 + 4,5\\ \Leftrightarrow 3\left| {5 - 2x} \right| = 12\\ \Leftrightarrow \left| {5 - 2x} \right| = 4\\ \Leftrightarrow \left[ \begin{array}{l}5 - 2x = 4\\5 - 2x = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 1\\2x = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{1}{2}\\x = \dfrac{9}{2}\end{array} \right..\end{array}\) Vậy nghiệm của phương trình là \(x = \dfrac{1}{2};x = \dfrac{9}{2}\) Nên tổng các nghiệm của phương trình là \(\dfrac{1}{2} + \dfrac{9}{2} = 5.\)
Câu 12 :
Số nghiệm của phương trình \(\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\) là
Đáp án : C Phương pháp giải :
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\) Từ đó ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\) Lời giải chi tiết :
\(\begin{array}{l}\;\left| {2x - 3} \right| - \left| {3x + 2} \right| = 0\\ \Leftrightarrow \left| {2x - 3} \right| = \left| {3x + 2} \right|\\ \Leftrightarrow \left[ \begin{array}{l}2x - 3 = 3x + 2\\2x - 3 = - (3x + 2)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\5x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\\x = \dfrac{1}{5}\end{array} \right..\end{array}\) Vậy phương trình có hai nghiệm là \(x = - 5;x = \dfrac{1}{5}\)
Câu 13 :
Hình vẽ nào dưới đây biểu diễn tập nghiệm của bất phương trình $2x - 8 \le 13 - 5x.$
Đáp án : C Phương pháp giải :
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương Cách biểu diễn nghiệm trên trục số Lời giải chi tiết :
$2x - 8 \le 13 - 5x \Leftrightarrow 2x + 5x \le 13 + 8 \Leftrightarrow 7x \le 21 \Leftrightarrow x \le 21:7 \Leftrightarrow x \le 3$ Vậy tập nghiệm của phương trình \(S = \left\{ {x/x \le 3} \right\}\) Biểu diễn tập nghiệm trên trục số 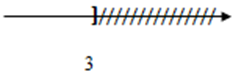
Câu 14 :
Nghiệm của phương trình \(\left| {x - 1} \right| = 3x - 2\) là:
Đáp án : A Phương pháp giải :
Xét phương trình \(\left| {A\left( x \right)} \right| = B\left( x \right)\;\;\;\left( 1 \right)\) * Cách 1: Ta thấy nếu $B(x) < 0$ thì không có giá trị nào của x thoả mãn vì giá trị tuyệt đối của mọi số đều không âm. Do vậy ta giải như sau: \(\left| {A\left( x \right)} \right| = B\left( x \right)\;\;\;\left( 1 \right)\) Điều kiện: $B(x)$ \( \ge 0\) (*) (1) Trở thành \(\left| {A\left( x \right)} \right| = B\left( x \right) \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\) (Đối chiếu giá trị x tìm được với điều kiện (*)) * Cách 2: Chia khoảng xét điều kiện bỏ dấu giá trị tuyệt đối: Nếu \(a \ge 0 \Rightarrow \left| a \right| = a.\) Nếu \(a < 0 \Rightarrow \left| a \right| = - a.\) Ta giải như sau: \(\left| {A\left( x \right)} \right| = B\left( x \right)\) (1) Nếu $A(x)$ \( \ge 0\) thì (1) trở thành: $A\left( x \right) = B\left( x \right)$ (Đối chiếu giá trị $x$ tìm được với điều kiện). Nếu $A (x ) < 0$ thì (1) trở thành: $ - {\rm{ }}A\left( x \right) = B\left( x \right)\;$ (Đối chiếu giá trị $x$ tìm được với điều kiện). Lời giải chi tiết :
\(\left| {x - 1} \right| = 3x - 2\) * Xét \(x - 1 \ge 0 \Leftrightarrow x \ge 1 \Rightarrow Pt \Leftrightarrow x - 1 = 3x - 2\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (KTMĐK) * Xét \(x - 1 < 0 \Leftrightarrow x < 1 \Rightarrow PT \Leftrightarrow - x + 1 = 3x - 2 \)\(\Leftrightarrow 4x = 3 \Leftrightarrow x = \dfrac{3}{4}\) (TMĐK) Vậy phương trình có một nghiệm \(x = \dfrac{3}{4}\) . Chú ý
Một số em không so sánh với điều kiện dẫn đến thừa nghiệm và chọn sai đáp án.
Câu 15 :
Số nguyên lớn nhất thỏa mãn bất phương trình ${(x - 2)^2} - {x^2} - 8x + 3 \ge 0$ là
Đáp án : B Phương pháp giải :
Phân tích hằng đẳng thức, biến đổi vế trái Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương. Lời giải chi tiết :
\(\begin{array}{l}{(x - 2)^2} - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow {x^2} - 4x + 4 - {x^2} - 8x + 3 \ge 0\\ \Leftrightarrow - 12x + 7 \ge 0\\ \Leftrightarrow x \le \dfrac{{ 7}}{{12}}\end{array}\) Vậy nghiệm của bất phương trình là \(x \le \dfrac{7}{{12}}.\) Nên số nguyên lớn nhất thỏa mãn bất phương trình là \(x = 0.\)
Câu 16 :
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
Đáp án : D Phương pháp giải :
Nhân đơn thức với đa thức Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương. Lời giải chi tiết :
\(\begin{array}{l}\;x(5x + 1) + 4(x + 3) > 5{x^2}\\ \Leftrightarrow 5{x^2} + x + 4x + 12 > 5{x^2}\\ \Leftrightarrow 5x > - 12\\ \Leftrightarrow x > \dfrac{{ - 12}}{5}\end{array}\) Vậy nghiệm của bất phương trình là \(x > - \dfrac{{12}}{5}.\) Số nguyên lớn nhất thỏa mãn bất phương trình là \(x = - 2.\)
Câu 17 :
Bất phương trình $\dfrac{{3x + 5}}{2} - 1 \le \dfrac{{x + 2}}{3} + x$ có nghiệm là:
Đáp án : D Phương pháp giải :
- Áp dụng quy tắc chuyển vế Lời giải chi tiết :
Ta có: Vậy nghiệm của bất phương trình là \(x \le - 5.\) Chú ý
Chuyển vế phải đổi dấu.
Câu 18 :
Bất phương trình $2(x - 1) - x > 3(x - 1) - 2x - 5$ có nghiệm là:
Đáp án : A Phương pháp giải :
- Quy tắc chuyển vế. Lời giải chi tiết :
Ta có: $\begin{array}{l}\;\;\;\;\;2(x - 1) - x > 3(x - 1) - 2x - 5\\ \Leftrightarrow 2x - 2 - x > 3x - 3 - 2x - 5\\ \Leftrightarrow x - 2 > x - 8\\ \Leftrightarrow - 2 > - 8\end{array}$
Câu 19 :
Tập nghiệm của bất phương trình \(\dfrac{{x - 3}}{{x + 4}} < 0\) là
Đáp án : B Phương pháp giải :
Giải bất phương trình dạng \(\dfrac{{A\left( x \right)}}{{B\left( x \right)}} > 0\) TH1: \(\left\{ \begin{array}{l}A\left( x \right) > 0\\B\left( x \right) > 0\end{array} \right.\) TH2: \(\left\{ \begin{array}{l}A\left( x \right) < 0\\B\left( x \right) < 0\end{array} \right.\) Lời giải chi tiết :
Xét \(\dfrac{{x - 3}}{{x + 4}} < 0.\) Trường hợp 1: \(\left\{ \begin{array}{l}x - 3 < 0\\x + 4 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 3\\x > - 4\end{array} \right. \Leftrightarrow - 4 < x < 3.\) Trường hợp 2: \(\left\{ \begin{array}{l}x - 3 > 0\\x + 4 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x < - 4\end{array} \right. \Rightarrow \) Bất phương trình vô nghiệm. Vậy \( - 4 < x < 3.\)
Câu 20 :
Tìm giá trị của x để biểu thức $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$ có giá trị dương
Đáp án : A Phương pháp giải :
- Phân thức nếu có giá trị dương thì tử và mẫu phải cùng dấu. - Đánh giá mẫu thức để suy ra điều kiện của tử thức. Lời giải chi tiết :
Xét $A = \dfrac{{5 - 2x}}{{{x^2} + 4}}$ Ta có: \({x^2} \ge 0\;\forall x \Rightarrow {x^2} + 4 > 0\;\forall x \Rightarrow A > 0 \Leftrightarrow 5 - 2x > 0 \Leftrightarrow x < \dfrac{5}{2}.\)
Câu 21 :
Phương trình \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\) có số nghiệm là
Đáp án : B Phương pháp giải :
- Lập bảng xét điều kiện bỏ dấu giá trị tuyệt đối. - Căn cứ vào bảng xét từng khoảng giải bài toán (đối chiếu với điều kiện tương ứng). Lời giải chi tiết :
Đặt \(\left| {x - 1} \right| + \left| {x - 3} \right| = 2x - 1\;\;\;\left( 1 \right)\) Xét: \(\begin{array}{l} + )\;\;x - 1 = 0 \Leftrightarrow x = 1\\ + )\;\;x - 3 = 0 \Leftrightarrow x = 3.\end{array}\) Ta có bảng xét dấu đa thức $x - 1$ và $x - 3$ dưới đây 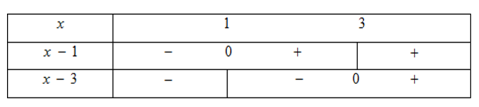 +) Xét khoảng \(x < 1\) ta có: \((1) \Leftrightarrow (1 - x) + (3 - x) = 2x - 1 \Leftrightarrow - 2x + 4 = 2x - 1 \Leftrightarrow 4x = 5 \Leftrightarrow x = \dfrac{5}{4}\) (Không thuộc khoảng đang xét) +) Xét khoảng \(1 \le x \le 3\) ta có \((1) \Leftrightarrow (x - 1) + (3 - x) = 2x - 1 \Leftrightarrow 2 = 2x - 1 \Leftrightarrow x = \dfrac{3}{2}(TM)\) +) Xét khoảng \(x > 3\) ta có: \((1) \Leftrightarrow (x - 1) + (x - 3) = 2x - 1 \Leftrightarrow 0.x = - 3\) (phương trình vô nghiệm) Vậy phương trình có nghiệm \(x = \dfrac{3}{2}\).
Câu 22 :
Nghiệm của bất phương trình \(\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\) là
Đáp án : A Phương pháp giải :
+) Với những bất phương trình chứa ẩn ở mẫu ta đặt điều kiện cho mẫu số khác 0. +) Quy đồng mẫu thức các phân thức +) Giải bất phương trình tìm điều kiện của $x$ sau đó đối chiếu với điều kiện để kết luận nghiệm của bất phương trình. Lời giải chi tiết :
\(\begin{array}{l}\;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{{x^2} - 1}}\\ \Leftrightarrow \;\dfrac{{x + 4}}{{x + 1}} + \dfrac{x}{{x - 1}} < \dfrac{{2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}\;\;\;\left( * \right)\end{array}\) Điều kiện \(\left\{ \begin{array}{l}x - 1 \ne 0\\x + 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right..\) \(\left( * \right) \Leftrightarrow \dfrac{{\left( {x + 4} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} + \dfrac{{x\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < \dfrac{{2{x^2}}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)\( \Leftrightarrow \dfrac{{{x^2} + 3x - 4 + {x^2} + x - 2{x^2}}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\) \( \Leftrightarrow \dfrac{{4x - 4}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0\)\( \Leftrightarrow \dfrac{{4\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0 \Leftrightarrow \dfrac{4}{{x + 1}} < 0\) mà \(4 > 0\) nên \(x + 1 < 0 \Leftrightarrow x < - 1.\) Kết hợp với điều kiện ta có bất phương trình có nghiệm \(x < - 1\). Chú ý
Một số em bỏ mẫu khi giải bất phương trình chứa ẩn ở mẫu dẫn đến sai nghiệm
Câu 23 :
Tập nghiệm của các bất phương trình ${x^2} + 2(x - 3) - 1 > x(x + 5) + 5$ và $\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}$ lần lượt là
Đáp án : C Phương pháp giải :
+) Qui đồng mẫu số nếu cần +) Áp dụng quy tắc chuyển vế và liên hệ giữa thứ tự và phép nhân. +) Khi nhân hay chia cả 2 vế của bất phương trình với một số dương thì bất phương trình không đổi chiều. +) Khi nhân hay chia cả 2 vế của bất phương trình với một số âm thì bất phương trình đổi chiều. Lời giải chi tiết :
$\begin{array}{l} + )\;\;{x^2} + 2(x - 3) - 1 > x(x + 5) + 5\\ \Leftrightarrow {x^2} + 2x - 6 - 1 > {x^2} + 5x + 5\\ \Leftrightarrow {x^2} + 2x - {x^2} - 5x > 5 + 6 + 1\\ \Leftrightarrow - 3x > 12\\ \Leftrightarrow x < - 4\end{array}$ \(\begin{array}{l} + )\;\;\dfrac{2}{3} - \dfrac{{3x - 6}}{2} > \dfrac{{1 + 3x}}{6}\\ \Leftrightarrow 2.2 - 3(3x - 6) > 1 + 3x\\ \Leftrightarrow 4 - 9x + 18 > 1 + 3x\\ \Leftrightarrow 12x < 21 \Leftrightarrow x < \dfrac{7}{4}\end{array}\) Vậy tập nghiệm của bất phương trình là \({S_1} = \left\{ {x/x < \dfrac{7}{4}} \right\}\)
Câu 24 :
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
Đáp án : A Phương pháp giải :
Sử dụng: Với $B(x) \ge 0$ thì \(\left| {A(x)} \right| = B(x) \Rightarrow \left[ \begin{array}{l}A(x) = B(x)\\A(x) = - B(x)\end{array} \right.\) Lời giải chi tiết :
\(\;\;\left| {{x^2} + 2x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 1 = 2\\{x^2} + 2x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = 0\\{x^2} + 2x + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 3x - x - 3 = 0\\{(x + 1)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x(x + 3) - (x + 3) = 0\\x + 1 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}(x + 3)(x - 1) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = - 1\end{array} \right..\) Vậy nghiệm của phương trình là $x{\rm{ }} = - 3;{\rm{ }}x = \pm 1.$ Tích các nghiệm của phương trình là \(\left( { - 3} \right).1.\left( { - 1} \right) = 3.\)
Câu 25 :
Chọn câu đúng, biết \(0 < a < b.\)
Đáp án : B Phương pháp giải :
Áp dụng thứ tự liên hệ giữa thứ tự và phép cộng, phép nhân. Biến đổi từ $ (a-b)^2 > 0$ với $0<a<b$ để tìm đáp án đúng. Lời giải chi tiết :
Với \(0 < a < b\) ta có \({\left( {a - b} \right)^2} > 0\) \( \Leftrightarrow {a^2} + {b^2} > 2ab \Leftrightarrow \dfrac{{{a^2}}}{{ab}} + \dfrac{{{b^2}}}{{ab}} > 2\,\,\left( {{\rm{do}}\,ab > 0} \right)\) \( \Leftrightarrow \dfrac{a}{b} + \dfrac{b}{a} > 2.\) Vậy với mọi \(0 < a < b\) ta luôn có \(\dfrac{a}{b} + \dfrac{b}{a} > 2.\) Chú ý
Một số bạn chọn nhầm đáp án C do không để ý điều kiện \(0 < a < b\) Nhận thấy với \(a;b > 0\) thì \(\dfrac{a}{b} + \dfrac{b}{a} = 2 \Leftrightarrow a = b = 1\) không thỏa mãn \(0 < a < b\)
Câu 26 :
Cho số thực \(x\) , chọn câu đúng nhất.
Đáp án : D Phương pháp giải :
Biến đổi tương đương các bất đẳng thức, sử dụng các hằng đẳng thức để chứng minh. Lời giải chi tiết :
+) Đáp án A: Bất đẳng thức tương đương với \({x^4} - 4x + 3 \ge 0\) \(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right)\left( {{x^3} + {x^2} + x - 3} \right) \ge 0 \\\Leftrightarrow \left( {x - 1} \right)\left( {\left( {{x^3} - 1} \right) + \left( {{x^2} + x - 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) + \left( {x - 1} \right)\left( {x + 2} \right)} \right) \ge 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1 + x + 2} \right) \ge 0 \\ \Leftrightarrow {\left( {x - 1} \right)^2}\left( {{x^2} + 2x + 3} \right) \ge 0\\ \Leftrightarrow {\left( {x - 1} \right)^2}\left[ {{{\left( {x + 1} \right)}^2} + 1} \right] \ge 0\end{array}\) (luôn đúng với mọi số thực $x$) Đẳng thức xảy ra khi và chỉ khi $x = 1.$ Nên A đúng. +) Đáp án B: Bất đẳng thức tương đương với \({x^4} - {x^2} - 4x + 5 > 0\) \( \Leftrightarrow {x^4} - 2{x^2} + 1 + {x^2} - 4x + 4 > 0 \)\( \Leftrightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\) Ta có: \(\left( {{x^2} - 1} \right) \ge 0,\,\,{\left( {x - 2} \right)^2} \ge 0 \)\( \Leftrightarrow \left( {{x^2} - 1} \right) + {\left( {x - 2} \right)^2} \ge 0\) Dấu bằng xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 1 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm 1\\x = 2\end{array} \right. \) điều này không xảy ra. \( \Rightarrow {\left( {{x^2} - 1} \right)^2} + {\left( {x - 2} \right)^2} > 0\) nên B đúng.
Câu 27 :
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
Đáp án : D Phương pháp giải :
Vận dụng tính chất không âm của giá trị tuyệt đối dẫn đến phương pháp bất đẳng thức. * Nhận xét: Tổng của các số không âm là một số không âm và tổng đó bằng 0 khi và chỉ khi các số hạng của tổng đồng thời bằng 0. * Cách giải chung: \(\left| A \right| + \left| B \right| = 0\) Bước1: Đánh giá: \(\left. \begin{array}{l}\left| A \right| \ge 0\\\left| B \right| \ge 0\end{array} \right\} \Rightarrow \left| A \right| + \left| B \right| \ge 0\) Bước 2: Khẳng định: \(\left| A \right| + \left| B \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) Lời giải chi tiết :
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) Ta có: \(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\) Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$ Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)
|














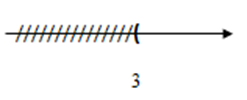
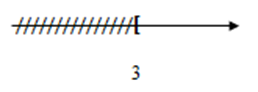
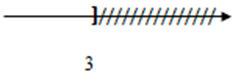
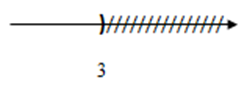





Danh sách bình luận