Đề số 4 - Đề kiểm tra học kì 2 - Toán lớp 5Tải vềĐáp án và lời giải chi tiết Đề số 4 - Đề kiểm tra học kì 2 - Toán lớp 5 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Phần 1. Trắc nghiệm (3 điểm) Câu 1. Chữ số 5 trong số 162,57 chỉ: A. 5 đơn vị B. 5 phần trăm C. 5 chục D.5 phần mười Câu 2. Hỗn số \(2\dfrac{3}{5}\) được viết dưới dạng phân số là: A. \(\dfrac{{21}}{5}\) B. \(\dfrac{{25}}{3}\) C. \(\dfrac{{13}}{{10}}\) D. \(\dfrac{{13}}{5}\) Câu 3. 5840g = .... kg A. 58,4kg B. 5,84kg C. 0,584kg D. 0,0584kg Câu 4. Đường kính một hình tròn là 0,6m. Diện tích hình tròn đó là : A. 1,884m2 B. 0,2826m2 C. 2,826m2 D. 2,86m2 Câu 5. Một huyện có 320ha đất trồng cây cà phê và 480ha đất trồng cây cao su. Hỏi diện tích đất trồng cây cao su bằng bao nhiêu phần trăm diện tích đất trồng cây cà phê? A. 150% B. 15% C. 1500% D. 105% Câu 6. Một bể cá hình hộp chữ nhật không nắp dài 0,6m ; rộng 0,4m ; cao 0,3m. Hỏi bể đó chứa được nhiều nhất bao nhiêu lít nước. A. 72 lít B. 124 lít C. 136 lít D. 144 lít Phần 2. Tự luận Bài 1. Đặt tính rồi tính: a) 83,45 + 26,6 b) 161,5 – 78,27 c) 28,3 × 3,6 d) 31,05 : 25 Bài 2. a) Tìm y, biết: 34,8 : y = 7,2 + 2,8 b) Tính : 21,22 + 9,072 x 10 + 24,72 : 12 Bài 3. Một người đi xe máy khởi hành từ A lúc 8 giờ 30 phút và đến B lúc 9 giờ 30 phút. Quãng đường AB dài 60km. Hãy tính vận tốc trung bình của xe máy với đơn vị đo là km/giờ? Bài 4. Một cái thùng không nắp dạng hình hộp chữ nhật chiều dài là 1,4m, chiều rộng bằng \(\dfrac{1}{2}\) chiều dài, chiều cao là 0,6m. Người ta sơn tất cả các mặt trong và ngoài thùng đó. Biết cứ 3m2 thì tốn 0,6kg sơn. Hỏi người ta sơn thùng đó hết bao nhiêu ki-lô-gam sơn ? Lời giải Phần 1. Trắc nghiệm Câu 1. Phương pháp: Xác định hàng của chữ số 5, từ đó tìm được giá trị của chữ số 5 trong số 162,57. Những chữ số ở bên trái dấu phẩy thuộc về phần nguyên, những chữ số ở bên phải dấu phấy thuộc về phần thập phân Cách giải: Chữ số 5 trong số 162,57 thuộc hàng phần mười nên có giá trị là 5 phần mười. Chọn D. Câu 2. Phương pháp: Để viết hỗn số \(2\dfrac{3}{5}\) dưới dạng phân số ta tìm tử số bằng cách lấy 2 nhân với 5 rồi cộng với 3, giữ nguyên mẫu số là 5. Cách giải: \(2\dfrac{3}{5} = \dfrac{{2 \times 5 + 3}}{5} = \dfrac{{13}}{5}\) Chọn D. Câu 3. Phương pháp: Áp dụng kiến thức: 1kg = 1000g hay 1g = \(\dfrac{1}{{1000}}\)kg. Cách giải: 5840g = 5kg 840g = 5\(\dfrac{{840}}{{1000}}\)kg = 5,840kg = 5,84kg. Chọn B. Câu 4. Phương pháp: - Tính bán kính = đường kính : 2. - Muốn tính diện tích của hình tròn ta lấy bán kính nhân với bán kính rồi nhân với số 3,14. Cách giải: Bán kính hình tròn đó là: 0,6 : 2 = 0,3 (m) Diện tích hình tròn đó là: 0,3 × 0,3 × 3,14 = 0,2826 (m2) Đáp số: 0,2826m2. Chọn B. Câu 5. Phương pháp: Để tìm tỉ số phần trăm diện tích đất trồng cây cao su và diện tích đất trồng cây cà phê ta lấy diện tích trồng cây cao su chia cho diện tích đất trồng cây cà phê, lấy thương tìm được nhân với 100 và viết thêm kí hiệu % vào bên phải tích tìm được. Cách giải: Diện tích đất trồng cây cao su chiếm số phần trăm diện tích đất trồng cây cà phê là: 480 : 320 = 1,5 1,5 = 150% Đáp số: 150%. Chọn A. Câu 6. Phương pháp: Số lít nước nhiều nhất mà bể đó chứa được chính bằng thể tích của bể. Tính thể tích bể nước ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo) Đổi kết quả vừa tìm được sang đơn vị đề-xi-mét khối rồi đổi sang đơn vị lít. Cách giải: Bể đó chứa được nhiều nhất số lít nước là: 0,6 × 0,4 × 0,3 = 0,072 (m3) 0,072m3 = 72dm3 = 72 lít. Đáp số: 72 lít. Chọn A. Phần 2. Tự luận Bài 1. Phương pháp: Đặt tính rồi tính theo các quy tắc đã học về phép cộng, trừ, nhân, chia số thập phân. Cách giải:
Bài 2. Phương pháp: a) - Tính giá trị vế phải trước. - y là số chia, muốn tìm số chia ta lấy số bị chia cho cho thương. b) Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau. Cách giải: a) 34,8 : y = 7,2 + 2,8 34,8 : y = 10 y = 34,8 : 10 y = 3,48 b) 21,22 + 9,072 × 10 + 24,72 : 12 = 21,22 + 90,72 + 2,06 = 111,94 + 2,06 = 114 Bài 3. Phương pháp: - Tìm thời gian người đó đi hết quãng đường AB: 9 giờ 30 phút – 8 giờ 30 phút. - Tìm vận tốc ta lấy quãng đường chia cho thời gian. Cách giải: Thời gian xe máy đi hết quảng đường AB là: 9 giờ 30 phút – 8 giờ 30 phút = 1 (giờ) Vận tốc trung bình của xe máy là: 60 : 1 = 60 (km/giờ) Đáp số: 60 km/giờ. Bài 4. Phương pháp: - Tính chiều rộng = chiều dài \(\times \,\dfrac{1}{2}\). - Diện tích sơn mặt trong bằng tổng diện tích xung quanh và diện tích một đáy. - Diện tích cần sơn bằng \(2\) lần diện tích sơn mặt trong. - Tìm tỉ số giữa diện tích cần sơn và \(3m^2\). Diện tích cần sơn gấp \(3m^2\) bao nhiêu lần thì khối lượng sơn cần dùng cũng gấp \(0,6kg\) bấy nhiêu lần. Cách giải: Chiều rộng của cái thùng đó là: \(1,4\times \,\dfrac{1}{2}=0,7\;(m^2)\) Diện tích xung quanh của cái thùng đó là: \((1,4+0,7) \times 2 \times 0,6 =2,52\;(m^2)\) Diện tích đáy của cái thùng đó là: \(1,4 \times 0,7 = 0,98\;(m^2)\) Diện tích khi sơn mặt trong và mặt ngoài của cái thùng đó là: \((2,52 + 0,98) \times 2 = 7\;(m^2)\) Người ta sơn thùng đó hết số ki-lô-gam sơn là: \( 7:3 \times 0,6 = 1,4\;(kg)\) Đáp số: \(1,4kg\). Loigiaihay.com
|














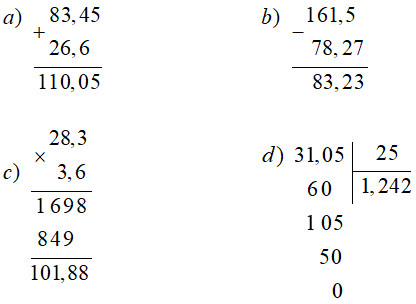






Danh sách bình luận