Đề kiểm tra học kì 1 Toán 5 - Đề số 32Đáp án và lời giải chi tiết Đề số 27 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán lớp 5 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
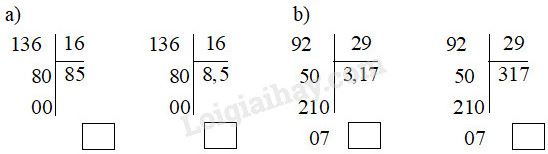
Đề bài Câu 1. Đúng ghi Đ, sai ghi S: Câu 2. Khoanh vào chữ đặt trước câu trả lời đúng: A. \(31,2:37 = 0,84\) (dư 12) B. \(31,2:37 = 0,84\) (dư 1,2) C. \(31,2:37 = 0,84\) (dư 0,12) D. \(31,2:37 = 0,84\) (dư 0,012) Câu 3. Đúng ghi Đ, sai ghi S: Câu 4. Đúng ghi Đ, sai ghi S: Tìm \(x\) biết: \(x \times 14 + \dfrac{7}{{100}} = 1141,07\) a) \(x = 81\) ☐ b) \(x = 81,5\) ☐ c) \(x = 815\) ☐ Câu 5. Khoanh vào chữ đặt trước câu trả lời đúng: 25 ô tô như nhau chở được 107 tấn hàng. Hỏi 15 ô tô như thế chở được bao nhiêu tấn hàng? A. 6,42 tấn B. 64,2 tấn C. 62,4 tấn Câu 6. Tìm \(x\), biết: a) \(x \times 9,1 + x \times 1,9 = 26,4\) b) \(x \times 9,9 + x:10 = 12,5\) Câu 7. Tổng hai số là 102,1. Tìm hai số đó biết nếu số thứ nhất gấp 5 lần số hạng thứ hai giữ nguyên thì tổng mới bằng 329,3. Câu 8. Một cửa hàng có 2007,8 tấn gạo. Ngày thứ nhất bán được \(\dfrac{1}{5}\) số gạo. Ngày thứ hai bán được \(\dfrac{3}{8}\) số gạo còn lại. Hỏi sau hai ngày bán cửa hàng còn lại bao nhiêu tấn gạo? Lời giải Câu 1. Phương pháp: Muốn chia một số thập phân với một số tự nhiên ta làm như sau: - Chia phần nguyên của số bị chia cho số chia. - Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia. - Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia. Cách giải: Ta đặt tính và thực hiện tính như sau: Vậy kết quả lần lượt là: S; Đ; S; Đ. Câu 2. Phương pháp: *) Muốn chia một số thập phân với một số tự nhiên ta làm như sau: - Chia phần nguyên của số bị chia cho số chia. - Viết dấu phẩy vào bên phải thương đã tìm trước khi lấy chữ số đầu tiên ở phần thập phân của số bị chia để tiếp tục thực hiện phép chia. - Tiếp tục chia với từng chữ số ở phần thập phân của số bị chia. *) Lưu ý: Để tìm số dư ta dóng thẳng cột dấu phẩy ở số bị chia xuống vị trí của số dư để tìm số dư của phép chia. Cách giải: Ta đặt tính và thực hiện tính như sau: Do đó: \(31,2 : 37 = 0,84\) dư \(0,12\). Thử lại: \(0,84 \times 37 + 0,12 = 31,2\). Chọn C. Câu 3. Phương pháp: Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau: - Viết dấu phẩy vào bên phải số thương. - Viết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp. - Nếu còn dư nữa, ta lại viết thêm bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi. Cách giải: Ta đặt tính và thực hiện tính như sau: Vậy kết quả lần lượt là: a) S ; Đ. b) Đ ; S. Câu 4. Phương pháp: Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. Cách giải: \(x \times 14 + \dfrac{7}{{100}} = 1141,07\) \(x \times 14 + 0,07 = 1141,07\) \(x \times 14 = 1141,07-0,07\) \(x \times 14 = 1141\) \(x=1141:14\) \(x=81,5\) Vậy kết quả lần lượt là: a) S; b) Đ; c) S. Câu 5. Phương pháp: - Tính số tấn hàng \(1\) ô tô chở được ta lấy số tấn hàng \(25\) ô tô chở được chia cho \(25\). - Tính số tấn hàng \(15\) ô tô chở được ta lấy số tấn hàng \(1\) ô tô chở được nhân với \(15\). Cách giải: \(1\) ô tô chở được số tấn hàng là: \(107: 25 = 4,28 \) (tấn) \(15\) ô tô chở được số tấn hàng là: \( 4,28 \times 15 = 64,2 \) (tấn) Đáp số: \(64,2\) tấn. Chọn B. Câu 6. Phương pháp: - Áp dụng tính chất nhân một số với một tổng: \(a\times (b+c) = a \times b + a\times c\). - Áp dụng quy tắc: Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết. Cách giải: a) \(x \times 9,1 + x \times 1,9 = 26,4\) \(x \times \left( {9,1 + 1,9} \right) = 26,4\) \(x \times 11 = 26,4\) \(x = 26,4:11 \) \(x= 2,4\) b) \(x \times 9,9 + x:10 = 12,5\) \(x \times 9,9 + x \times \dfrac{1}{10} = 12,5\) (vì \(10=\dfrac{10}{1}\)) \(x \times 9,9 + x \times 0,1 = 12,5\) \(x \times \left( {9,9 + 0,1} \right) = 12,5\) \(x \times 10 = 12,5\) \(x = 12,5:10 \) \(x= 1,25\) Câu 7. Phương pháp: - Nếu số thứ nhất gấp 5 lần số hạng thứ hai giữ nguyên thì tổng sẽ tăng thêm \(4\) lần số hạng thứ nhất. Hiệu giữa tổng mới và tổng cũ chính bằng \(4\) lần số hạng thứ nhất, từ đó ta tìm được số hạng thứ nhất. - Số hạng thứ hai \(=\) tổng ban đầu \(-\) số hạng thứ nhất. Cách giải: Nếu số thứ nhất gấp 5 lần số hạng thứ hai giữ nguyên thì tổng sẽ tăng thêm \(4\) lần số hạng thứ nhất. Hiệu giữa tổng mới và tổng cũ là: \(329,3 - 102,1 = 227,2\) Do đó, \(4\) lần số hạng thứ nhất là \(227,2\). Số hạng thứ nhất là: \(227,2:4 = 56,8\) Số hạng thứ hai là: \(102,1 - 56,8 = 45,3\) Đáp số: Số thứ nhất: \(56,8\); Số thứ hai: \(45,3\). Câu 8. Phương pháp: - Tìm số gạo bán ngày thứ nhất \(=\) số gạo ban đầu cửa hàng có \(\times\,\dfrac{1}{5}\). - Tìm số gạo còn lại sau khi bán ngày thứ nhất \(=\) số gạo ban đầu cửa hàng có \(-\) số gạo bán ngày thứ nhất. - Tìm số gạo bán ngày thứ nhất \(=\) số gạo còn lại sau khi bán ngày thứ nhất \(\times\,\dfrac{3}{8}.\) - Tìm số gạo còn lại sau hai ngày bán \(=\) số gạo còn lại sau khi bán ngày thứ nhất \(-\) số gạo bán ngày thứ hai (hoặc lấy số gạo ban đầu cửa hàng có trừ đi tổng số gạo bán trong hai ngày). Cách giải: Ngày thứ nhất bán được số tấn gạo là: \(2007,8 \times \dfrac{1}{5} = 401,56\) (tấn) Số gạo còn lại sau khi bán ngày thứ nhất là: \(2007,8 - 401,56 = 1606,24\) (tấn) Ngày thứ hai bán được số tấn gạo là: \(1606,24 \times \dfrac{3}{8} = 602,34\) (tấn) Sau hai ngày bán cửa hàng còn lại số tấn gạo là: \(1606,24 - 602,34 = 1003,9\) (tấn) Đáp số: \(1003,9\) tấn. Loigiaihay.com
|
















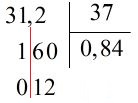







Danh sách bình luận