Trắc nghiệm Các dạng toán về phân số với tử số và mẫu số là số nguyên Toán 6 Chân trời sáng tạoĐề bài
Câu 1 :
Trong các cách viết sau đây, cách viết nào cho ta phân số:
Câu 2 :
Phần tô màu trong hình sau biểu diễn phân số nào? 
Câu 3 :
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
Câu 4 :
Cho tập \(A = \left\{ {1; - 2;3;4} \right\}\). Có bao nhiêu phân số có tử số và mẫu số thuộc \(A\) mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
Câu 5 :
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
Câu 6 :
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
Câu 7 :
Tổng các số \(a;b;c\) thỏa mãn \(\dfrac{6}{9} = \dfrac{{12}}{a} = \dfrac{b}{{ - 54}} = \dfrac{{ - 738}}{c}\) là:
Câu 8 :
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\) Số cặp phân số bằng nhau trong những phân số trên là:
Câu 9 :
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
Câu 10 :
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
Câu 11 :
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
Câu 12 :
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
Câu 13 :
Viết số nguyên \( - 16\) dưới dạng phân số ta được:
Câu 14 :
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Lời giải và đáp án
Câu 1 :
Trong các cách viết sau đây, cách viết nào cho ta phân số:
Đáp án : B Phương pháp giải :
Dựa vào định nghĩa phân số: \(\dfrac{a}{b}\) là phân số với \(a,b \in \mathbb{Z},\,b \ne 0\). Lời giải chi tiết :
+) \(\dfrac{{12}}{0}\) không là phân số vì mẫu số bằng $0.$ +) \(\dfrac{3}{{0,25}}\) không là phân số vì mẫu số là số thập phân. +) \(\dfrac{{4,4}}{{11,5}}\) không là phân số vì tử số và mẫu số là số thập phân. +) \(\dfrac{{ - 4}}{5}\) là phân số vì \( - 4;\,5\, \in \mathbb{Z} \) và mẫu số là $5$ khác $0.$
Câu 2 :
Phần tô màu trong hình sau biểu diễn phân số nào?
Đáp án : B Phương pháp giải :
Quan sát hình vẽ, đếm số ô vuông có trong hình và số ô vuông được tô màu, phân số biểu thị có tử là số ô vuông tô màu và mẫu là tổng số ô vuông có trong hình. Lời giải chi tiết :
Trong hình có \(2\) ô vuông tô màu và tổng tất cả \(8\) ô vuông nên phân số biểu thị là \(\dfrac{2}{8} = \dfrac{1}{4}\)
Câu 3 :
Tìm số nguyên \(x\) biết \(\dfrac{{35}}{{15}} = \dfrac{x}{3}?\)
Đáp án : A Phương pháp giải :
Sử dụng kiến thức: Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau) Lời giải chi tiết :
\(\begin{array}{l}\dfrac{{35}}{{15}} = \dfrac{x}{3}\\35.3 = 15.x\\x = \dfrac{{35.3}}{{15}}\\x = 7\end{array}\) Vậy \(x = 7\)
Câu 4 :
Cho tập \(A = \left\{ {1; - 2;3;4} \right\}\). Có bao nhiêu phân số có tử số và mẫu số thuộc \(A\) mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
Đáp án : B Phương pháp giải :
- Liệt kê các phân số thỏa mãn bài toán. - Đếm số phân số và kết luận đáp án đúng. Lời giải chi tiết :
Các phân số thỏa mãn bài toán là: $\dfrac{1}{{ - 2}},\dfrac{3}{{ - 2}},\dfrac{4}{{ - 2}},\dfrac{{ - 2}}{1},\dfrac{{ - 2}}{3},\dfrac{{ - 2}}{4}$ Vậy có tất cả \(6\) phân số.
Câu 5 :
Cho biểu thức \(C = \dfrac{{11}}{{2n + 1}}\) . Tìm tất cả các giá trị của $n$ nguyên để giá trị của $C$ là một số tự nhiên.
Đáp án : C Phương pháp giải :
- $C$ là số tự nhiên suy ra \(C\) là số nguyên hay $2n + 1$ là ước của $11$ Lời giải chi tiết :
Vì \(C \in N\) nên \(\frac{11}{2n+1} \in N.\) Để \(\frac{11}{2n+1} \in N\) thì \(11 \vdots (2n+1)\) và \((2n+1) > 0\) hay \((2n+1) \in \left\{ { 1; 11} \right\}\) Ta có bảng: 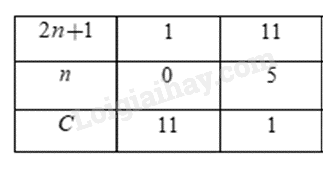 Vì \(C \in N\) nên ta nhận các giá trị \(n = 0;n = 5\)
Câu 6 :
Có bao nhiêu giá trị nguyên dương của \(n\) để \(\dfrac{9}{{4n + 1}}\) đạt giá trị nguyên.
Đáp án : A Phương pháp giải :
Phân số \(\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)\) là một số nguyên nếu \(b\) là ước của $a$ Lời giải chi tiết :
Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\) Ta có bảng: 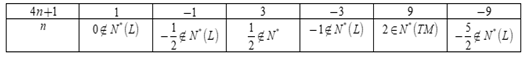 Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)
Câu 7 :
Tổng các số \(a;b;c\) thỏa mãn \(\dfrac{6}{9} = \dfrac{{12}}{a} = \dfrac{b}{{ - 54}} = \dfrac{{ - 738}}{c}\) là:
Đáp án : B Phương pháp giải :
Sử dụng kiến thức: Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau) Lời giải chi tiết :
Ta có: \(\dfrac{6}{9} = \dfrac{{12}}{a} \Rightarrow 6.a = 9.12\) \( \Rightarrow a = \dfrac{{9.12}}{6} = 18\) \(\dfrac{6}{9} = \dfrac{b}{{ - 54}} \Rightarrow 6.\left( { - 54} \right) = 9.b\) \( \Rightarrow b = \dfrac{{6.\left( { - 54} \right)}}{9} = - 36\) \(\dfrac{6}{9} = \dfrac{{ - 738}}{c} \Rightarrow 6.c = 9.\left( { - 738} \right)\) \( \Rightarrow c = \dfrac{{9.\left( { - 738} \right)}}{6} = - 1107\) Vậy \(a + b + c\) \( = 18 + \left( { - 36} \right) + \left( { - 1107} \right) = - 1125\)
Câu 8 :
Cho các phân số: \(\dfrac{{15}}{{60}};\dfrac{{ - 7}}{5};\dfrac{6}{{15}};\dfrac{{28}}{{ - 20}};\dfrac{3}{{12}}\) Số cặp phân số bằng nhau trong những phân số trên là:
Đáp án : D Phương pháp giải :
- Ta sẽ chia các phân số thành \(2\) loại: phân số dương, phân số âm (chú ý phân số dương và phân số âm không thể bằng nhau) - Tìm các cặp phân số bằng nhau trong những phân số dương và các cặp phân số bằng nhau trong những phân số âm rồi kết luận. Sử dụng kiến thức: - Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau) - Định nghĩa các phân số dương, phân số âm: + Phân số âm: là phân số có tử và mẫu là các số nguyên trái dấu. + Phân số dương: là phân số có tử và mẫu là các số nguyên cùng dấu. Lời giải chi tiết :
- Các phân số dương: \(\dfrac{{15}}{{60}};\dfrac{6}{{15}};\dfrac{3}{{12}}\) + Vì \(15.15 \ne 60.6\) nên \(\dfrac{{15}}{{60}} \ne \dfrac{6}{{15}}\) + Vì \(6.12 \ne 15.3\) nên \(\dfrac{6}{{15}} \ne \dfrac{3}{{12}}\) + Vì \(15.12 = 60.3\) nên \(\dfrac{{15}}{{60}} = \dfrac{3}{{12}}\) - Các phân số âm: \(\dfrac{{ - 7}}{5};\dfrac{{28}}{{ - 20}}\) Vì \(\left( { - 7} \right).\left( { - 20} \right) = 5.28\) nên \(\dfrac{{ - 7}}{5} = \dfrac{{28}}{{ - 20}}\) Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.
Câu 9 :
Tìm tập hợp các số nguyên \(n\) để \(A = \dfrac{{3n - 5}}{{n + 4}}\) có giá trị là số nguyên.
Đáp án : B Phương pháp giải :
- Biến đổi \(A\) về dạng \(A = a + \dfrac{b}{{n + 4}}\) với \(a,b \in Z\) - Để \(A\) nguyên thì \(n + 4 \in U\left( b \right)\) Lời giải chi tiết :
Ta có: \(A = \dfrac{{3n - 5}}{{n + 4}} = \dfrac{{3n + 12 - 12 - 5}}{{n + 4}}\)\( = \dfrac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\) \( = \dfrac{{3\left( {n + 4} \right)}}{{n + 4}} + \dfrac{{ - 17}}{{n + 4}} = 3 + \dfrac{{ - 17}}{{n + 4}}\) Vì \(n \in Z\) nên để \(A \in Z\) thì \(n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\) Ta có bảng: 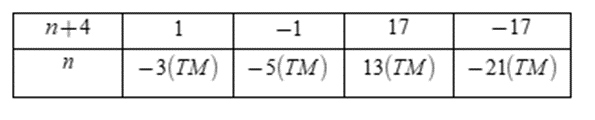 Vậy \(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)
Câu 10 :
Có bao nhiêu cặp số nguyên \(\left( {x;y} \right)\) thỏa mãn \(\dfrac{x}{5} = \dfrac{3}{y}\) và \(x > y?\)
Đáp án : A Phương pháp giải :
Sử dụng kiến thức: Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau) Lời giải chi tiết :
Ta có: \(\dfrac{x}{5} = \dfrac{3}{y}\)\( \Rightarrow x.y = 5.3 = 15\) Mà \(15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\) và \(x,y \in Z,x > y\) nên \(\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\)
Câu 11 :
Tìm \(x;y\) biết \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) và \(x - y = 5.\)
Đáp án : C Phương pháp giải :
- Rút \(x\) theo \(y\) từ điều kiện đơn giản rồi thay vào đẳng thức hai phân số bằng nhau. - Sử dụng kiến thức hai phân số bằng nhau để tìm \(y,\) từ đó suy ra \(x\) - Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau) Lời giải chi tiết :
Ta có: \(x - y = 5 \Rightarrow x = y + 5\) thay vào \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) ta được: \(\begin{array}{l}\dfrac{{y + 5 - 4}}{{y - 3}} = \dfrac{4}{3}\\\dfrac{{y + 1}}{{y - 3}} = \dfrac{4}{3}\\3\left( {y + 1} \right) = 4\left( {y - 3} \right)\\3y + 3 = 4y - 12\\3y - 4y = - 12 - 3\\ - y = - 15\\y = 15\\ \Rightarrow x = 15 + 5 = 20\end{array}\) Vậy \(x = 20;y = 15\)
Câu 12 :
Tìm số nguyên \(x\) biết rằng \(\dfrac{x}{3} = \dfrac{{27}}{x}\) và \(x < 0.\)
Đáp án : C Phương pháp giải :
Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) gọi là bằng nhau nếu \(a.d = b.c\) (tích chéo bằng nhau). Lời giải chi tiết :
\(\begin{array}{l}\dfrac{x}{3} = \dfrac{{27}}{x}\\x.x = 81\\{x^2} = 81\end{array}\) Ta có: \(x = 9\) hoặc \(x = - 9\) Kết hợp điều kiện \(x < 0\) nên có một giá trị \(x\) thỏa mãn là: \(x = - 9\)
Câu 13 :
Viết số nguyên \( - 16\) dưới dạng phân số ta được:
Đáp án : C Lời giải chi tiết :
Viết số nguyên \( - 16\) dưới dạng phân số ta được: \(\dfrac{{ - 16}}{1}\)
Câu 14 :
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là:
Đáp án : D Lời giải chi tiết :
Phân số \(\dfrac{{ - 9}}{7}\) được đọc là: Âm chín phần bảy
|
