Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo

Trắc nghiệm Hình chữ nhật - Hình thoi. Hình bình hành - Hình thang cân Toán 6 Chân trời sáng tạo

Làm đề thi

Đề bài

Câu 1 :

Trong những khẳng định sau, khẳng định nào sai?

  • A
    Hình bình hành có 4 đỉnh
  • B
    Hình bình hành có bốn cạnh
  • C
    Hình có bốn đỉnh là hình bình hành
  • D

    Hình bình hành có hai cạnh đối song song.

Câu 2 :

Cho hình chữ nhật ABCD, phát biểu nào đúng?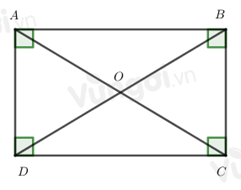

  • A
    \(AB = AC\)
  • B
    \(AC = DO\)
  • C

    \(AC = BD\)

  • D
    \(OB = AC\)
Câu 3 :

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:

 

A. \(16cm\)

B. \(17cm\)

C. \(18cm\)

D. \(19cm\)   

Câu 4 :

Chọn phát biểu sai trong các phát biểu sau?

  • A
    Hình thoi có bốn đỉnh
  • B
    Hình thoi có hai cặp cạnh đối bằng nhau
  • C
    Hình thoi có hai cặp cạnh đối song song
  • D
    Hình có bốn đỉnh là hình thoi
Câu 5 :

Trong các hình sau, các hình là hình thoi là: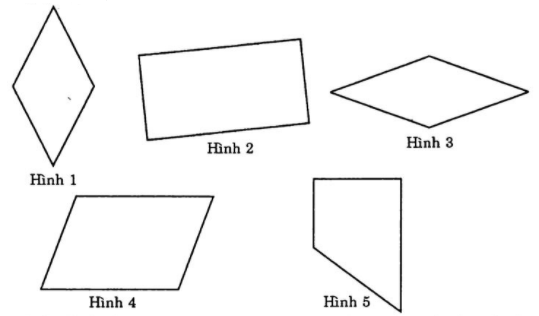

  • A
    Hình 1, Hình 2
  • B
    Hình 3, Hình 4
  • C
    Hình 1, Hình 3
  • D
    Hình 3, Hình 5
Câu 6 :

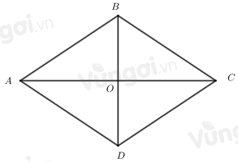Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:

  • A
    \(OB = 5\,cm\)
  • B
    \(AO = 5\,cm\)
  • C
    \(OD = 5\,cm\)
  • D
    \(OC = \,20\,cm\)
Câu 7 :

Trong các hình dưới đây, hình nào là hình thang cân:

  • A
    Hình a
  • B
    Hình b
  • C
    Hình c
  • D
    Hình d
Câu 8 :

Điền số thích hợp vào ô trống:

Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). 


Vậy chiều cao tương ứng với cạnh đáy đó là 

\(cm\).

Câu 9 :

Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:

  • A
    EH
  • B
    HF
  • C
    EF
  • D
    HG
Câu 10 :

Tên các đỉnh của hình thang cân EFGH dưới đây là

  • A
    E, G, O, H
  • B
    E, F, O, G
  • C
    E, F, G, H
  • D
    E, F, G, H, O
Câu 11 :

Điền số thích hợp vào ô trống:

Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). 


Vậy chiều cao của hình bình hành đó là 

\(dm\).

Câu 12 :

Hình thang cân có:

  • A

    1 cạnh bên

  • B
    2 cạnh bên
  • C
    3 cạnh bên
  • D
    4 cạnh bên
Câu 13 :

Trong các hình sau, hình nào là hình thoi?

Câu 14 :

Hình thang cân EFGH có:

  • A
    EF  là đường chéo
  • B
    EF và GH là đường chéo
  • C
    EH và FG là đường chéo
  • D
    EG và HF là đường chéo
Câu 15 :

Quan sát hình thang cân EFGH, cạnh EH bằng?

  • A
    EF
  • B
    HG
  • C
    HF
  • D
    FG
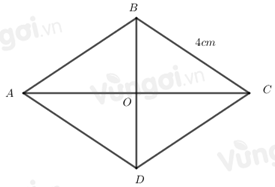
Câu 16 : Cho hình thoi \(ABCD\) có \(BC = 4\,\,cm\), khẳng định nào sau đây đúng:
  • A
    \(AB = 2\,\,cm\)
  • B
    \(AD = 8\,\,cm\)
  • C
    \(DC = 4\,\,cm\)
  • D
    \(AB = 8\,\,cm\)
Câu 17 :

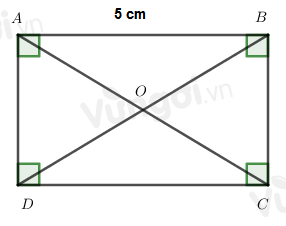Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:

  • A
    \(BC\, = 5\,cm\)
  • B
    \(AC = 5\,cm\)
  • C
    \(AD = \,5\,cm\)
  • D
    \(DC = 5\,cm\)
Câu 18 :

Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

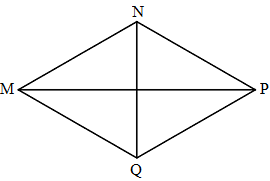
Trong hình thoi MNPQ:

MN và PQ không bằng nhau.

Đúng
Sai

MN không song song với MQ

Đúng
Sai

Các cặp cạnh đối diện song song.

Đúng
Sai

MN = NP = PQ = QM

Đúng
Sai
Câu 19 :

Chọn phát biểu sai?

  • A
    Hình có bốn đỉnh là hình chữ nhật
  • B
    Hình chữ nhật có bốn đỉnh
  • C
    Hình chữ nhật có hai cặp cạnh đối song song.
  • D
    Hình chữ nhật có hai đường chéo bằng nhau
Câu 20 :

Trong các hình sau, hình nào là hình bình hành?

 

 

Câu 21 :

Trong các hình dưới đây, hình nào là hình bình hành?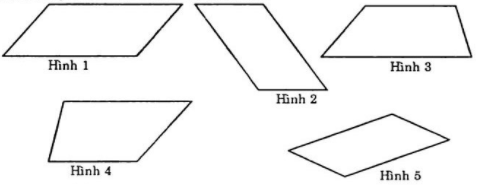

  • A
    Hình 1, hình 2, hình 4
  • B
    Hình 2, hình 3, hình 4
  • C
    Hình 1, hình 4, hình 5
  • D
    Hình 1, hình 2, hình 5
Câu 22 :

Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là: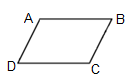

  • A
    AB và AD
  • B
    AD và DC
  • C
    BC và AD
  • D
    DC và BC

Lời giải và đáp án

Câu 1 :

Trong những khẳng định sau, khẳng định nào sai?

  • A
    Hình bình hành có 4 đỉnh
  • B
    Hình bình hành có bốn cạnh
  • C
    Hình có bốn đỉnh là hình bình hành
  • D

    Hình bình hành có hai cạnh đối song song.

Đáp án : C

Phương pháp giải :

Dựa vào cách nhận biết hình bình hành.

Lời giải chi tiết :

Hình bình hành có 4 đỉnh, có bốn cạnh, hai cạnh đối song song => A, B, D đúng

Hình có bốn đỉnh chưa chắc là hình bình hành, ví dụ:

Câu 2 :

Cho hình chữ nhật ABCD, phát biểu nào đúng?

  • A
    \(AB = AC\)
  • B
    \(AC = DO\)
  • C

    \(AC = BD\)

  • D
    \(OB = AC\)

Đáp án : C

Phương pháp giải :

Trong hình chữ nhật hai đường chéo bằng nhau

Lời giải chi tiết :

Trong hình chữ nhật hai đường chéo bằng nhau nên \(AC = BD\) => Đáp án C đúng

Đáp án A sai do AB là cạnh, AC là đường chéo nên chúng không bằng nhau.

Đáp án B sai do AC là đường chéo, DO là một nửa đường chéo còn lại nên chúng không bằng nhau.

Đáp án D sai do OB là một nửa đường chéo, AC là đường chéo còn lại nên chúng không bằng nhau.

Câu 3 :

Độ dài đáy của hình bình hành có chiều cao \(24cm\) và diện tích là \(432c{m^2}\) là:

 

A. \(16cm\)

B. \(17cm\)

C. \(18cm\)

D. \(19cm\)   

Đáp án

C. \(18cm\)

Phương pháp giải :

Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính độ dài cạnh đáy \(a\) là \(a = S:h\).

Lời giải chi tiết :

Độ dài đáy của hình bình hành đó là:

          \(432:24 = 18\,\,(cm)\)

                             Đáp số: \(18cm\).

Câu 4 :

Chọn phát biểu sai trong các phát biểu sau?

  • A
    Hình thoi có bốn đỉnh
  • B
    Hình thoi có hai cặp cạnh đối bằng nhau
  • C
    Hình thoi có hai cặp cạnh đối song song
  • D
    Hình có bốn đỉnh là hình thoi

Đáp án : D

Phương pháp giải :
Dựa vào cách nhận biết hình thoi.
Lời giải chi tiết :

Hình có bốn đỉnh chưa chắc là hình thoi, ví dụ: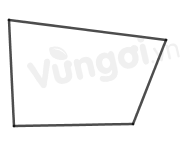

=> D sai

Câu 5 :

Trong các hình sau, các hình là hình thoi là:

  • A
    Hình 1, Hình 2
  • B
    Hình 3, Hình 4
  • C
    Hình 1, Hình 3
  • D
    Hình 3, Hình 5

Đáp án : C

Phương pháp giải :

Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

Lời giải chi tiết :

Hình thoi là hình tứ giác có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

=> Hình 1 và Hình 3 là hình thoi

Câu 6 :

Cho hình thoi \(ABCD\) (\(AC > BD\)) có \(AC = 10\,\,\,cm\), khẳng định nào sau đây đúng:

  • A
    \(OB = 5\,cm\)
  • B
    \(AO = 5\,cm\)
  • C
    \(OD = 5\,cm\)
  • D
    \(OC = \,20\,cm\)

Đáp án : B

Phương pháp giải :
Hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết :

Do hai đường chéo của hình thoi cắt nhau tại trung điểm của mỗi đường nên \(AO = OC = 10:2 = 5\,cm\)

=> B đúng, C sai

Vì \(BD < AC\) nên \(OB = OD < \frac{{10}}{2} = 5\,cm\).

=> A và C sai.

Câu 7 :

Trong các hình dưới đây, hình nào là hình thang cân:

  • A
    Hình a
  • B
    Hình b
  • C
    Hình c
  • D
    Hình d

Đáp án : B

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình thang cân.

Lời giải chi tiết :

Quan sát hình ta thấy Hình b là hình thang cân.

Câu 8 :

Điền số thích hợp vào ô trống:

Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). 


Vậy chiều cao tương ứng với cạnh đáy đó là 

\(cm\).

Đáp án

Một bình hành có diện tích là \(8d{m^2}\) và độ dài cạnh đáy là \(32cm\). 


Vậy chiều cao tương ứng với cạnh đáy đó là 

\(cm\).

Phương pháp giải :

- Đổi \(8d{m^2}\) sang đơn vị đo là \(c{m^2}\).

- Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,:\,a\).

Lời giải chi tiết :

Đổi \(8d{m^2} = 800c{m^2}\)

Chiều cao của hình bình hành đó là:

         \(800:32 = 25\,\,(cm)\)

                          Đáp số: \(25cm\).

Vậy đáp án đúng điền vào ô trống là \(25\).

Câu 9 :

Quan sát hình thang cân EFGH, đoạn EG bằng đoạn:

  • A
    EH
  • B
    HF
  • C
    EF
  • D
    HG

Đáp án : B

Phương pháp giải :

Sử dụng: Trong hình thang cân hai đường chéo bằng nhau.

Lời giải chi tiết :

Do góc EG và HF là hai đường chéo của hình thang EFGH nên:

\(EG=HF\).

Câu 10 :

Tên các đỉnh của hình thang cân EFGH dưới đây là

  • A
    E, G, O, H
  • B
    E, F, O, G
  • C
    E, F, G, H
  • D
    E, F, G, H, O

Đáp án : C

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình thang cân.

Lời giải chi tiết :

Hình thang cân EFGH có bốn đỉnh là: E, F, G, H.

Câu 11 :

Điền số thích hợp vào ô trống:

Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). 


Vậy chiều cao của hình bình hành đó là 

\(dm\).

Đáp án

Một hình bình hành có diện tích là \(1855d{m^2}\) và độ dài cạnh đáy là \(53dm\). 


Vậy chiều cao của hình bình hành đó là 

\(dm\).

Phương pháp giải :

Từ công thức tính diện tích hình bình hành: \(S = a \times h\), ta có thể suy ra công thức tính chiều cao \(h\) là \(h = S\,\,:\,\,a\).

Lời giải chi tiết :

Chiều cao của hình bình hành đó là:

        \(1855:53 = 35\,\,(dm)\)

                          Đáp số: \(35dm\).

Vậy đáp án đúng điền vào ô trống là \(35\).

Câu 12 :

Hình thang cân có:

  • A

    1 cạnh bên

  • B
    2 cạnh bên
  • C
    3 cạnh bên
  • D
    4 cạnh bên

Đáp án : B

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình thang cân.

Lời giải chi tiết :

Hình thang cân có 2 cạnh bên.

Câu 13 :

Trong các hình sau, hình nào là hình thoi?

Đáp án

Phương pháp giải :

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

Lời giải chi tiết :

Quan sát các hình đã cho ta thấy hình thứ nhất và thứ hai từ trên xuống là hình thoi.

Hình thứ ba là hình thang và hình thứ tư là hình bình hành.

Câu 14 :

Hình thang cân EFGH có:

  • A
    EF  là đường chéo
  • B
    EF và GH là đường chéo
  • C
    EH và FG là đường chéo
  • D
    EG và HF là đường chéo

Đáp án : D

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình thang cân.

Lời giải chi tiết :

Hình thang cân EFGH có: EG và HF là đường chéo.

Câu 15 :

Quan sát hình thang cân EFGH, cạnh EH bằng?

  • A
    EF
  • B
    HG
  • C
    HF
  • D
    FG

Đáp án : D

Phương pháp giải :

Sử dụng: Trong hình thang cân hai cạnh bên bằng nhau.

Lời giải chi tiết :

Do góc EH và FG là cạnh bên của hình thang EFGH nên:

\(EH=FG\)

Câu 16 : Cho hình thoi \(ABCD\) có \(BC = 4\,\,cm\), khẳng định nào sau đây đúng:
  • A
    \(AB = 2\,\,cm\)
  • B
    \(AD = 8\,\,cm\)
  • C
    \(DC = 4\,\,cm\)
  • D
    \(AB = 8\,\,cm\)

Đáp án : C

Phương pháp giải :

Hình thoi có bốn cạnh bằng nhau.

Lời giải chi tiết :

Hình thoi có bốn cạnh bằng nhau nên \(AB = BC = DC = AD = 4\,cm\).

=> \(DC = 4\,\,cm\).

Câu 17 :

Cho hình chữ nhật ABCD, \(AB = 5cm\), chọn khẳng định đúng:

  • A
    \(BC\, = 5\,cm\)
  • B
    \(AC = 5\,cm\)
  • C
    \(AD = \,5\,cm\)
  • D
    \(DC = 5\,cm\)

Đáp án : D

Phương pháp giải :

Trong hình chữ nhật hai cạnh đối bằng nhau.

Lời giải chi tiết :

Trong hình chữ nhật ABCD, cạnh đối của cạnh AB là DC nên \(AB = DC = 5\,cm\)

Câu 18 :

Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:

Trong hình thoi MNPQ:

MN và PQ không bằng nhau.

Đúng
Sai

MN không song song với MQ

Đúng
Sai

Các cặp cạnh đối diện song song.

Đúng
Sai

MN = NP = PQ = QM

Đúng
Sai
Đáp án

MN và PQ không bằng nhau.

Đúng
Sai

MN không song song với MQ

Đúng
Sai

Các cặp cạnh đối diện song song.

Đúng
Sai

MN = NP = PQ = QM

Đúng
Sai
Phương pháp giải :

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

Lời giải chi tiết :

Trong hình thoi MNPQ ta có: 

- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.

- Bốn cạnh bằng nhau: MN = NP = PQ = QM.

Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.

Câu 19 :

Chọn phát biểu sai?

  • A
    Hình có bốn đỉnh là hình chữ nhật
  • B
    Hình chữ nhật có bốn đỉnh
  • C
    Hình chữ nhật có hai cặp cạnh đối song song.
  • D
    Hình chữ nhật có hai đường chéo bằng nhau

Đáp án : A

Phương pháp giải :

Sử dụng dấu hiệu nhận biết hình chữ nhật

Lời giải chi tiết :

Hình chữ nhật có bốn đỉnh, hai cặp cạnh đối song song, hai đường chéo bằng nhau.

=> Đáp án B, C, D đúng.

Hình có 4 đỉnh chưa chắc là hình chữ nhật ví dụ: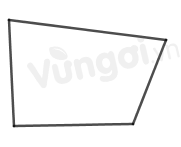

Câu 20 :

Trong các hình sau, hình nào là hình bình hành?

 

 

Đáp án

 

Lời giải chi tiết :

Quan sát các hình đã cho ta thấy hình thứ nhất và hình thứ tư từ trên xuống có hai cặp cạnh đối diện song song và bằng nhau nên các hình đó là hình bình hành.

Câu 21 :

Trong các hình dưới đây, hình nào là hình bình hành?

  • A
    Hình 1, hình 2, hình 4
  • B
    Hình 2, hình 3, hình 4
  • C
    Hình 1, hình 4, hình 5
  • D
    Hình 1, hình 2, hình 5

Đáp án : D

Phương pháp giải :

Hình bình hành là tứ giác có hai cặp cạnh đối diện song song và bằng nhau.

Lời giải chi tiết :

Các hình là hình bình hành là: Hình 1, hình 2, hình 5

Câu 22 :

Cho hình bình hành \(ABCD\), cặp cạnh song song với nhau là:

  • A
    AB và AD
  • B
    AD và DC
  • C
    BC và AD
  • D
    DC và BC

Đáp án : C

Phương pháp giải :

Trong hình bình hành hai cặp cạnh đối diện song song với nhau.

Lời giải chi tiết :

Vì trong hình bình hành hai cặp cạnh đối diện song song với nhau nên BC song song với AD

=> C đúng

Bài liên quan
close