Trắc nghiệm Bài 6: Góc Toán 6 Chân trời sáng tạoĐề bài
Câu 1 :
Chọn câu sai.
Câu 2 :
Cho hình vẽ sau 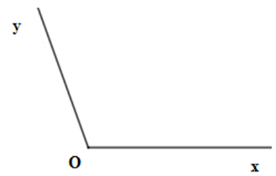 Chọn câu đúng.
Câu 3 :
Kể tên các góc có trên hình vẽ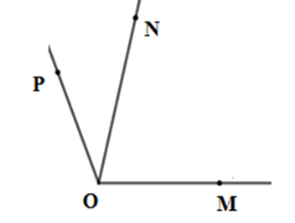 
Câu 4 :
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau 
Câu 5 :
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
Câu 6 :
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
Câu 7 :
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
Câu 8 :
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
Câu 9 :
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Câu 10 :
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
Lời giải và đáp án
Câu 1 :
Chọn câu sai.
Đáp án : B Phương pháp giải :
Sử dụng kiến thức về góc và so sánh hai góc Để so sánh hai góc ta so sánh số đo của chúng Lời giải chi tiết :
Ta có: + Góc là hình gồm hai tia chung gốc nên A đúng + Góc bẹt là góc có hai cạnh là hai tia đối nhau nên B sai vì hai tia chung gốc chưa chắc đã đối nhau + Hai góc bằng nhau có số đo bằng nhau nên C đúng + Hai góc có số đo bằng nhau thì bằng nhau nên D đúng
Câu 2 :
Cho hình vẽ sau Chọn câu đúng.
Đáp án : A Phương pháp giải :
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc. Lời giải chi tiết :
Góc trên hình là góc \(\widehat {xOy}\), đỉnh \(O\) , cạnh \(Ox\) và \(Oy\) .
Câu 3 :
Kể tên các góc có trên hình vẽ
Đáp án : B Phương pháp giải :
Quan sát hình vẽ, xác định các tia phân biệt chung gốc \(O\) từ đó tìm các góc tạo thành. Lời giải chi tiết :
Các góc tạo thành là: \(\widehat {MON};\widehat {NOP};\,\widehat {MOP}\)
Câu 4 :
Kể tên tất cả các góc có một cạnh là \(Om\) có trên hình vẽ sau
Đáp án : D Phương pháp giải :
Xác định các tia chung gốc \(O\) từ đó xác định các góc có một cạnh là \(Om.\) Lời giải chi tiết :
Các góc cần tìm là \(\widehat {xOm};\,\widehat {mOn};\widehat {mOy}\) .
Câu 5 :
Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)
Đáp án : B Phương pháp giải :
Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt. Lời giải chi tiết :
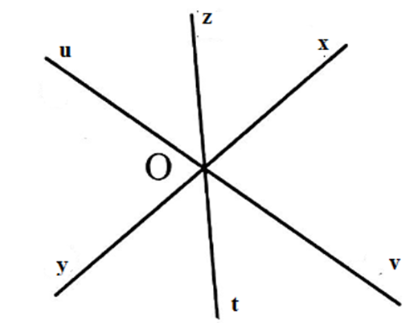 Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\) tạo thành là \(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .
Câu 6 :
Cho \(n\left( {n \ge 2} \right)\) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có \(28\) góc tạo thành thì \(n\) bằng bao nhiêu?
Đáp án : A Phương pháp giải :
Sử dụng: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\) Từ đó tìm ra \(n.\) Lời giải chi tiết :
Từ đề bài ta có \(\dfrac{{n\left( {n - 1} \right)}}{2} = 28\) nên \(n\left( {n - 1} \right) = 56\) mà \(56 = 8.7\), lại có $(n-1)$ và $n$ là hai số tự nhiên liên tiếp nên \(n = 8.\) Vậy \(n = 8.\)
Câu 7 :
Cho trước \(4\) tia chung gốc \(O.\) Vẽ thêm \(3\) tia gốc \(O\) không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh \(O?\)
Đáp án : C Phương pháp giải :
Ta sử dụng công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\) + Tính số góc ban đầu + Tính số góc sau khi thêm + Tính số góc tăng thêm Lời giải chi tiết :
Số góc tạo thành khi có \(4\) tia chung gốc là \(\dfrac{{4.\left( {4 - 1} \right)}}{2} = 6\) góc Số góc tạo thành khi có thêm ba tia chung gốc \(O\) nữa là \(\dfrac{{7.\left( {7 - 1} \right)}}{2} = 21\) góc Số góc tăng thêm là \(21 - 6 = 15\) góc
Câu 8 :
Giả sử có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) thì số góc tạo thành là
Đáp án : D Phương pháp giải :
+ Xác định số lượng các tia phân biệt chung gốc \(O.\) + Tính góc theo công thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\) Lời giải chi tiết :
Vì có \(n\left( {n \ge 2} \right)\) đường thẳng đồng qui tại \(O\) nên số các tia chung gốc tạo thành là \(2n\) tia. Số góc tạo thành là \(\dfrac{{2n\left( {2n - 1} \right)}}{2} = n\left( {2n - 1} \right)\) góc.
Câu 9 :
Cho góc \(xOy\) khác góc bẹt, tia \(Oz\) nằm giữa hai tia \(Ox;Oy\). Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\). Lấy điểm \(A \in Ox;\,B \in Oy\), đường thẳng \(AB\) cắt tia \(Oz;Ot\) theo thứ tự tại \(M;N\). Chọn câu sai.
Đáp án : C Phương pháp giải :
Sử dụng: Khi hai tia \(Ox;Oy\) không đối nhau, điểm \(M\) là điểm nằm bên trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox;Oy\). Lời giải chi tiết :
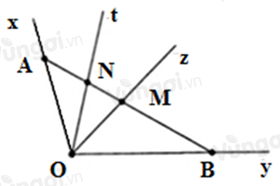 Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) mà điểm \(N\) thuộc tia \(Ot\) nên điểm \(N\) nằm trong góc \(xOz\). Do đó A đúng. Tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(N\) và điểm \(A\) nằm cùng phía đối với điểm \(M.\) Tia \(Oz\) nằm giữa hai tia \(Ox;Oy\) nên điểm \(A;B\) nằm khác phía đối với điểm \(M.\) Suy ra điểm \(N\) và điểm \(B\) nằm khác phía đối với điểm \(M\), do đó điểm \(M\) nằm trong góc \(yOt.\) Do đó B đúng, D đúng. Vì \(A \in Ox\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oz\) nên điểm \(A\) không nằm trong góc \(tOz.\) Do đó C sai.
Câu 10 :
Cho \(9\) tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là
Đáp án : C Phương pháp giải :
Ta sử dụng kiến thức: Nếu có \(n\,\left( {n \ge 2} \right)\) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là \(\dfrac{{n\left( {n - 1} \right)}}{2}\) Lời giải chi tiết :
Số góc tạo thành là \(\dfrac{{9.\left( {9 - 1} \right)}}{2} = 36\) góc.
|
