Trắc nghiệm Hình vuông – Tam giác đều – Lục giác đều Toán 6 Chân trời sáng tạoĐề bài
Câu 1 :
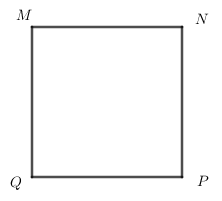 Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Câu 2 :
Chọn phát biểu sai?
Câu 3 :
Phát biểu nào sau đây sai?
Câu 4 :
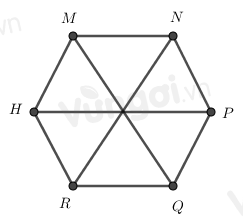
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Câu 5 :
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
Câu 6 :
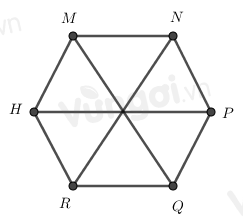 Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Câu 7 :
Chọn phát biểu sai:
Câu 8 :
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Câu 9 :
Hình dưới đây có mấy hình tam giác?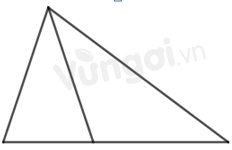 
Câu 10 :
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?
Câu 11 :
Hình dưới đây có tất cả bao nhiêu hình vuông? 
Lời giải và đáp án
Câu 1 :
Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
Đáp án : A Phương pháp giải :
Trong hình vuông, hai cặp cạnh đối song song với nhau. Lời giải chi tiết :
Trong hình vuông \(MNPQ\) có hai cặp cạnh đối song song với nhau là: + \(MN\) và \(PQ\). + \(MQ\) và \(NP\) => Đáp án A đúng.
Câu 2 :
Chọn phát biểu sai?
Đáp án : B Phương pháp giải :
Sử dụng dấu hiệu nhận biết của hình vuông. Lời giải chi tiết :
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Câu 3 :
Phát biểu nào sau đây sai?
Đáp án : C Phương pháp giải :
Sử dụng dấu hiệu nhận biết lục giác đều. Lời giải chi tiết :
Các đáp án A, B, D đúng. Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.
Câu 4 :
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : D Phương pháp giải :
- Trong hình lục giác đều: + 6 cạnh bằng nhau + 3 đường chéo chính bằng nhau. Lời giải chi tiết :
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\) => A đúng Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\) => B, C đúng. Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau => D sai
Câu 5 :
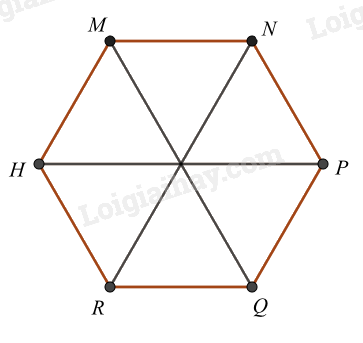
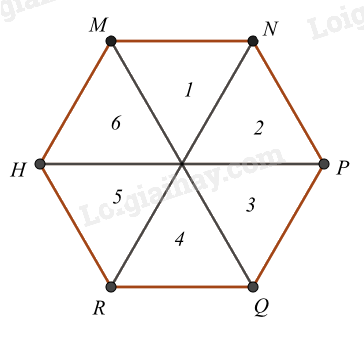
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
Đáp án : D Phương pháp giải :
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều Lời giải chi tiết :
Ta đánh số như hình trên Hình lục giác đều được tạo thành bởi 6 hình tam giác đều nên các hình tam giác đều là: 1, 2, 3, 4, 5, 6. Vậy có 6 tam giác đều.
Câu 6 :
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
Đáp án : B Phương pháp giải :
- Trong hình lục giác đều: + 6 cạnh bằng nhau + 3 đường chéo chính bằng nhau. Lời giải chi tiết :
Đáp án B sai do MQ là đường chéo chính, sửa lại: 6 cạnh là MN, NP, PQ, HR, QR, HM
Câu 7 :
Chọn phát biểu sai:
Đáp án : C Lời giải chi tiết :
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Câu 8 :
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
Đáp án : D Lời giải chi tiết :
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\) => Chọn D
Câu 9 :
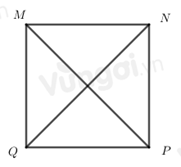
Hình dưới đây có mấy hình tam giác?
Đáp án : C Phương pháp giải :
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ Lời giải chi tiết :
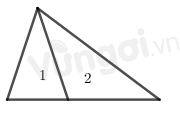 Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên => Có tất cả 3 hình tam giác
Câu 10 :
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?
Đáp án : D Phương pháp giải :
Trong hình vuông: - Bốn cạnh bằng nhau. - Hai đường chéo bằng nhau. Lời giải chi tiết :
Hình vuông \(MNPQ\) có: \(MN = NP = PQ = MQ\) => Đáp án A, B, C đúng. Đáp án D sai do \(MN\) là cạnh của hình vuông, \(MP\) là đường chéo nên \(MN = MP\) là sai.
Câu 11 :
Hình dưới đây có tất cả bao nhiêu hình vuông?
Đáp án : B Phương pháp giải :
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ. Lời giải chi tiết :
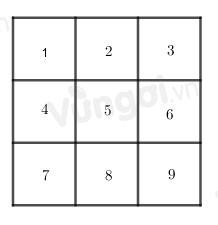 Ta đánh số như hình trên: + 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9. + 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689. + 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ. Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.
|
