Bài tập trắc nghiệm Toán 6 - Chân trời sáng tạo

Trắc nghiệm Bài 3: Hai đường thẳng cắt nhau, song song. Tia Toán 6 Chân trời sáng tạo

Làm đề thi

Đề bài

Câu 1 :

Cho hai đường thẳng \(a;b.\) Khi đó \(a;b\) có thể

  • A

    Song song

  • B

    Trùng nhau

  • C

    Cắt nhau

  • D

    Cả ba đáp án trên đều đúng

Câu 2 :

Chọn câu đúng.

  • A

    Qua hai điểm phân biệt có vô số đường thẳng

  • B

    Có vô số điểm cùng thuộc một đường thẳng

  • C

    Hai đường thẳng phân biệt thì song song

  • D

    Trong ba điểm thẳng hàng thì có hai điểm nằm giữa

Câu 3 :

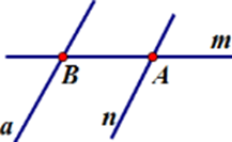
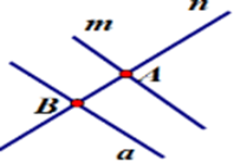
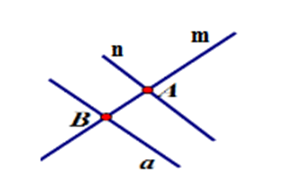
Cho đường thẳng $m$ và đường thẳng $n$ cắt nhau tại $A,$ đường thẳng $a$ không cắt đường thẳng $m$ nhưng cắt đường thẳng $n$ tại $B.$ Hãy chọn hình vẽ đúng trong các hình sau?

  • A
  • B
  • C
  • D

Cho hình vẽ, biết kéo dài \(a,b\) ta cũng không xác định được điểm chung.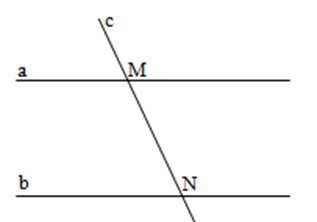

Câu 4

Hai đường thẳng nào song song với nhau?

  • A.

    \(a\) và \(c\)

  • B.

    \(b\) với \(c\)   

  • C.

    \(a\) và \(b\)    

  • D.

    \(c\) và \(MN\)

Câu 5

Hãy chỉ ra những cặp đường thẳng cắt nhau và giao điểm của chúng.

  • A.

    \(a,c\) cắt nhau tại \(M\) và \(b,c\) cắt nhau tại \(N\)

  • B.

    \(b,c\) cắt nhau tại \(M\) và \(a,c\) cắt nhau tại \(N\)

  • C.

    \(a,b\) cắt nhau tại \(M\) và \(b,c\) cắt nhau tại \(N\)

  • D.

    \(a,c\) cắt nhau tại \(M\) và \(a,b\) cắt nhau tại \(N\)

Câu 6 :

Kể tên các tia trong hình vẽ sau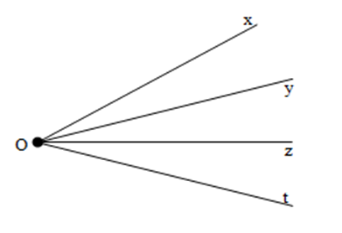

  • A

    \(Ox\)  

  • B

    \(Ox,Oy,Oz,Ot\)                     

  • C

    \(Ox,Oy,Oz\)

  • D

    \(xO,yO,zO,tO\)

Câu 7 :

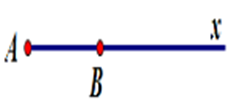
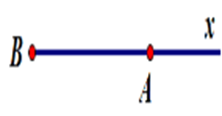
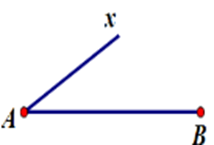
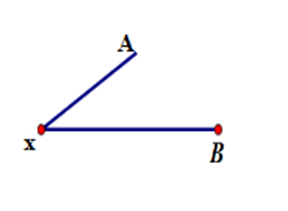
Cho $AB$ và $Ax$ là hai tia trùng nhau. Hãy chọn hình vẽ đúng.

  • A
  • B
  • C
  • D
Câu 8 :

Cho tia $AB,$ lấy $M$ thuộc tia $AB.$ Khẳng định nào sau đây đúng?

  • A

    \(M\) và \(A\) nằm cùng phía so với \(B\)

  • B

    \(M\) và \(B\) nằm cùng phía so với \(A\)

  • C

    \(A\) và \(B\) nằm cùng phía so với \(M\)

  • D

    \(M\) nằm giữa \(A\) và \(B\)

Câu 9 :

Cho hai tia đối nhau $MA$ và $MB,$ $X$ là $1$ điểm thuộc tia $MA.$ Trong $3$ điểm $X,{\rm{ }}M,{\rm{ }}B$ điểm nào nằm giữa hai điểm còn lại?

  • A

    chưa kết luận được

  • B

    \(X\)

  • C

    \(B\)  

  • D

    \(M\)

Câu 10 :

Trong hình vẽ sau, có bao nhiêu tia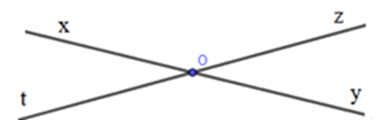

  • A

    \(2\)  

  • B

    \(0\)  

  • C

    \(4\)        

  • D

    \(1\)

Câu 11 :

Vẽ hình theo cách diễn đạt sau:

+ Vẽ hai tia phân biệt $Ox$ và \(Oy\) chung gốc nhưng không đối nhau, không trùng nhau

+ Vẽ đường thẳng \(aa'\) cắt hai tia \(Ox;\,Oy\) theo thứ tự tại \(A\) và \(B\)(khác \(O\))

+ Vẽ điểm \(C\) nằm giữa hai điểm \(A;B\) sau đó vẽ tia \(Oz\) đi qua \(C\)

Có bao nhiêu tia phân biệt trên hình vẽ thu được.

  • A

    \(6\)  

  • B

    \(12\)   

  • C

    \(9\)  

  • D

    \(15\)

Cho hình vẽ sau

Câu 12

Một cặp tia đối nhau là:

  • A.

    \(Ut,UV\)  

  • B.

    \(Us,Vt\)         

  • C.

    \(Vs,Vt\)  

  • D.

    \(Vs,Ut\)

Câu 13

Kể tên các tia trùng nhau trên hình vẽ

  • A.

    Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)  

  • B.

    Tia \(Us\) và tia \(Vs\); tia \(VU\) và tia \(Vs\)

  • C.

    Tia \(Ut\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)           

  • D.

    Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Us\)

Vẽ đường thẳng $mn.$ Lấy điểm $O$ trên đường thẳng $mn,$ trên tia $Om$ lấy điểm $A,$ trên tia $On$ lấy điểm $B.$

Câu 14

Một cặp tia đối nhau gốc $O$  là:

  • A.

    \(OB,AO\)                 

  • B.

    \(mO,nO\)    

  • C.

    \(OA,Om\)     

  • D.

    \(OA,On\)

Câu 15

Một cặp tia đối nhau gốc $B$  là:

  • A.

    \(Bn,BA\)                  

  • B.

    \(BO,BA\) 

  • C.

    \(Bm,BA\)

  • D.

    \(OB,Bn\)

Câu 16

Có bao nhiêu cặp tia trùng nhau gốc \(O?\)

  • A.

    \(2\)

  • B.

    \(4\)    

  • C.

    \(3\)             

  • D.

    \(0\)

Câu 17

Trong ba điểm \(O;A;B\) thì điểm nào nằm giữa hai điểm còn lại?

  • A.

    \(A\)  

  • B.

    \(O\)    

  • C.

    \(B\)            

  • D.

    chưa kết luận được

Vẽ hai đường thẳng \(xy\) và \(mn\) cắt nhau tại \(O.\)

Câu 18

Kể tên các cặp tia đối nhau.

  • A.

    Không có cặp tia đối nhau                 

  • B.

    Cặp tia \(Ox,On\) và cặp tia \(Om,Oy\)

  • C.

    Cặp tia \(Ox,Oy\) và cặp tia \(Om,On\)                

  • D.

    Cặp tia \(Ox,Om\) và cặp tia \(Oy,On\)

Câu 19

Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Kể tên các tia trùng nhau.

  • A.

    \(OA,On\) và \(OB,Om\) và \(Ox,Oy\)  

  • B.

    \(OA,On\) và \(OB,Om\)

  • C.

    \(OA,On\) và \(Ox,Oy\)         

  • D.

    \(OA,OB\) và \(OB,Om\)

Câu 20

Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Lấy điểm $C$ sao cho điểm \(O\) nằm giữa hai điểm \(B\) và \(C.\) Khi đó điểm \(C\) thuộc tia nào?

  • A.

    \(Ox,Oy\)                   

  • B.

    \(Oy,OA\)    

  • C.

    \(Om,OA\)     

  • D.

    \(On,OA\)

Cho hình vẽ sau

Câu 21

Tia nào trùng với tia $Ay$?

  • A.

    Tia $Ax$        

  • B.

    Tia $OB,By$

  • C.

    Tia $BA$       

  • D.

    Tia $AO,AB$

Câu 22

Hai tia $Ax$ và $By$ có vị trí như thế nào với nhau

  • A.

    Đối nhau        

  • B.

    Trùng nhau

  • C.

    Không đối nhau, không trùng nhau   

  • D.

    Vừa đối nhau, vừa trùng nhau

Lời giải và đáp án

Câu 1 :

Cho hai đường thẳng \(a;b.\) Khi đó \(a;b\) có thể

  • A

    Song song

  • B

    Trùng nhau

  • C

    Cắt nhau

  • D

    Cả ba đáp án trên đều đúng

Đáp án : D

Phương pháp giải :

Vị trí của hai đường thẳng:

Hai đường thẳng $a,{\rm{ }}b$ bất kì có thể:

+ Trùng nhau: có vô số điểm chung.

+ Cắt nhau: chỉ có $1$ điểm chung - điểm chung đó gọi là giao điểm.

+ Song song: không có điểm chung nào.

Lời giải chi tiết :

Hai đường thẳng \(a,b\) bất kì có thể trùng nhau, song song hoặc cắt nhau.

Câu 2 :

Chọn câu đúng.

  • A

    Qua hai điểm phân biệt có vô số đường thẳng

  • B

    Có vô số điểm cùng thuộc một đường thẳng

  • C

    Hai đường thẳng phân biệt thì song song

  • D

    Trong ba điểm thẳng hàng thì có hai điểm nằm giữa

Đáp án : B

Phương pháp giải :

Nhận xét tính đúng sai của từng đáp án dựa vào các kiến thức về sự xác định đường thẳng đi qua hai điểm, số điểm thuộc đường thẳng, vị trí tương đối của hai đường thẳng, vị trí của ba điểm thẳng hàng.

Lời giải chi tiết :

Đáp án A: Qua hai điểm phân biệt có một và chỉ một đường thẳng nên A sai.

Đáp án B: Có vô số điểm cùng thuộc một đường thẳng nên B đúng.

Đáp án C: Hai đường thẳng phân biệt thì có thể song song hoặc cắt nhau nên C sai.

Đáp án D: Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa hai điểm còn lại nên D sai.

Câu 3 :

Cho đường thẳng $m$ và đường thẳng $n$ cắt nhau tại $A,$ đường thẳng $a$ không cắt đường thẳng $m$ nhưng cắt đường thẳng $n$ tại $B.$ Hãy chọn hình vẽ đúng trong các hình sau?

  • A
  • B
  • C
  • D

Đáp án : C

Phương pháp giải :

Quan sát các hình vẽ ở từng đáp án, so sánh với các dữ kiện bài cho và kết luận.

Sử dụng lý thuyết về vị trí của hai đường thẳng:

+ Cắt nhau: chỉ có 1 điểm chung - điểm chung đó gọi là giao điểm.

+ Song song: không có điểm chung nào.

Lời giải chi tiết :

Hình A: Có đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $m$ tại $B$ nhưng không cắt đường thẳng $n$ (trái với đề bài là $a$ cắt $n$ tại $B$ ) (loại) 
Hình B: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,{\rm{ }}a$ cắt m tại $C,$ cắt $n$ tại $B$ (trái với đề bài là $a$ không cắt $m$) (loại) 
Hình C: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $n$ tại $B$ và $a$ không cắt $m$  (thỏa mãn) 

Hình D: Đường thẳng $a$ cắt đường thẳng $m$ tại $B$ (trái với đề bài là \(a\) không cắt \(m\))  (loại) 

Cho hình vẽ, biết kéo dài \(a,b\) ta cũng không xác định được điểm chung.

Câu 4

Hai đường thẳng nào song song với nhau?

  • A.

    \(a\) và \(c\)

  • B.

    \(b\) với \(c\)   

  • C.

    \(a\) và \(b\)    

  • D.

    \(c\) và \(MN\)

Đáp án : C

Phương pháp giải :

Hai đường thẳng song song nếu chúng không có điểm chung nào.

Lời giải chi tiết :

Từ hình vẽ ta thấy hai đường thẳng \(a,b\) không có điểm chung nên chúng song song.

Hai đường thẳng \(a,c\) có điểm \(M\) chung hay hai đường thẳng \(a,c\) không song song.

Hai đường thẳng \(b,c\) có điểm \(N\) chung hay hai đường thẳng \(b,c\) không song song.

Ngoài ra hai đường thẳng \(MN\) và \(c\) trùng nhau nên chúng cũng không song song.

Câu 5

Hãy chỉ ra những cặp đường thẳng cắt nhau và giao điểm của chúng.

  • A.

    \(a,c\) cắt nhau tại \(M\) và \(b,c\) cắt nhau tại \(N\)

  • B.

    \(b,c\) cắt nhau tại \(M\) và \(a,c\) cắt nhau tại \(N\)

  • C.

    \(a,b\) cắt nhau tại \(M\) và \(b,c\) cắt nhau tại \(N\)

  • D.

    \(a,c\) cắt nhau tại \(M\) và \(a,b\) cắt nhau tại \(N\)

Đáp án : A

Phương pháp giải :

Quan sát hình vẽ và nhận xét vị trí của các cặp đường thẳng để tìm cặp đường thẳng cắt nhau.

Lời giải chi tiết :

Hai đường thẳng \(a,c\) có điểm \(M\) chung.

Hai đường thẳng \(b,c\) có điểm \(N\) chung.

Câu 6 :

Kể tên các tia trong hình vẽ sau

  • A

    \(Ox\)  

  • B

    \(Ox,Oy,Oz,Ot\)                     

  • C

    \(Ox,Oy,Oz\)

  • D

    \(xO,yO,zO,tO\)

Đáp án : B

Phương pháp giải :

Sử dụng định nghĩa tia:

- Hình gồm điểm $O$ và một phần đường thẳng bị chia ra bởi điểm $O$ được gọi là một tia gốc $O,$ còn gọi là một nửa đường thẳng gốc $O.$

Lời giải chi tiết :

Các tia trong hình vẽ là: \(Ox,Oy,Oz,Ot\)

Câu 7 :

Cho $AB$ và $Ax$ là hai tia trùng nhau. Hãy chọn hình vẽ đúng.

  • A
  • B
  • C
  • D

Đáp án : A

Phương pháp giải :

Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.

Xét các tia trong hình vẽ ở mỗi đáp án xem chúng trùng nhau hay không và kết luận.

Lời giải chi tiết :

Hình A: Hai tia $AB$ và $Ax$ chung gốc $A\;$
Hai tia $AB$ và $Ax$ cùng nằm trên nửa đường thẳng chứa tia $Ax$
Nên hai tia $AB$ và $Ax$ là hai tia trùng nhau.

Hình B: Hai tia \(AB,Ax\) đối nhau nên loại.

Hình C: Hai tia \(AB,Ax\) chỉ có chung mỗi điểm \(A\) nên không trùng nhau.

Hình D: Hình vẽ tia \(Ax\) chưa đúng.

Câu 8 :

Cho tia $AB,$ lấy $M$ thuộc tia $AB.$ Khẳng định nào sau đây đúng?

  • A

    \(M\) và \(A\) nằm cùng phía so với \(B\)

  • B

    \(M\) và \(B\) nằm cùng phía so với \(A\)

  • C

    \(A\) và \(B\) nằm cùng phía so với \(M\)

  • D

    \(M\) nằm giữa \(A\) và \(B\)

Đáp án : B

Phương pháp giải :

Vẽ hình theo hai trường hợp $M$ có thể nằm giữa $A$ và $B$ hoặc $B$ nằm giữa $A$ và $M$ rồi loại đáp án.

Lời giải chi tiết :

Vì $M$ thuộc tia $AB$ nên $M$ có thể nằm giữa $A$ và $B$ hoặc $B$ nằm giữa $A$ và $M$
Ta có hình vẽ: 

Th1:

Từ hình vẽ ta thấy đáp án C sai nên loại C.

Th2: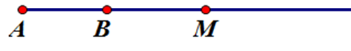

Từ hình vẽ ta thấy đáp án A, D sai nên loại A, D.

Cả hai hình vẽ đều có \(M\) và \(B\) nằm cùng phía so với \(A\) nên B đúng.

Câu 9 :

Cho hai tia đối nhau $MA$ và $MB,$ $X$ là $1$ điểm thuộc tia $MA.$ Trong $3$ điểm $X,{\rm{ }}M,{\rm{ }}B$ điểm nào nằm giữa hai điểm còn lại?

  • A

    chưa kết luận được

  • B

    \(X\)

  • C

    \(B\)  

  • D

    \(M\)

Đáp án : D

Phương pháp giải :

Có thể sử dụng phương pháp sau: 
Nếu $Ax$ và $Ay$ là hai tia đối nhau, mà điểm $M$ thuộc tia $Ax,$ điểm $N$ thuộc tia $Ay$ thì điểm $A$ nằm giữa hai điểm $M$ và $N$

Lời giải chi tiết :

Theo đề bài ta có hình vẽ:

Vì hai tia \(MA,MB\) đối nhau và \(X\) thuộc tia \(MA\) và \(B\) thuộc tia \(MB\) nên điểm \(M\) nằm giữa hai điểm \(B,X\)

Câu 10 :

Trong hình vẽ sau, có bao nhiêu tia

  • A

    \(2\)  

  • B

    \(0\)  

  • C

    \(4\)        

  • D

    \(1\)

Đáp án : C

Phương pháp giải :

Liệt kê các tia có trong hình vẽ với chú ý điểm \(O\) thuộc hai đường thẳng \(xy,zt\)

Lời giải chi tiết :

Có các tia là $Ox,Oy,Oz,Ot.$

Vậy có $4$ tia.

Câu 11 :

Vẽ hình theo cách diễn đạt sau:

+ Vẽ hai tia phân biệt $Ox$ và \(Oy\) chung gốc nhưng không đối nhau, không trùng nhau

+ Vẽ đường thẳng \(aa'\) cắt hai tia \(Ox;\,Oy\) theo thứ tự tại \(A\) và \(B\)(khác \(O\))

+ Vẽ điểm \(C\) nằm giữa hai điểm \(A;B\) sau đó vẽ tia \(Oz\) đi qua \(C\)

Có bao nhiêu tia phân biệt trên hình vẽ thu được.

  • A

    \(6\)  

  • B

    \(12\)   

  • C

    \(9\)  

  • D

    \(15\)

Đáp án : B

Phương pháp giải :

Vẽ hình, liệt kê các tia phân biệt dựa vào kiến thức:

Hai tia không trùng nhau còn được gọi là hai tia phân biệt.

Lời giải chi tiết :

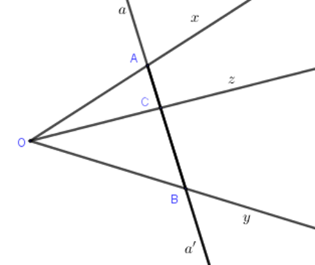Các tia phân biệt trong hình là:

\(Ox,Oy,Oz,Aa,Aa',Ca,Ca',Ba,Ba',Ax,By,Cz\)

Có tất cả \(12\) tia phân biệt.

Cho hình vẽ sau

Câu 12

Một cặp tia đối nhau là:

  • A.

    \(Ut,UV\)  

  • B.

    \(Us,Vt\)         

  • C.

    \(Vs,Vt\)  

  • D.

    \(Vs,Ut\)

Đáp án : C

Phương pháp giải :

Định nghĩa hai tia đối nhau:

Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Lời giải chi tiết :

Các cặp tia đối nhau có trong hình là:

$Us,Uv$ hoặc \(Us,Ut;\) \(Vt,VU\) hoặc \(Vt,Vs\)

Đối chiếu với các đáp án ta thấy đáp án C đúng.

Câu 13

Kể tên các tia trùng nhau trên hình vẽ

  • A.

    Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)  

  • B.

    Tia \(Us\) và tia \(Vs\); tia \(VU\) và tia \(Vs\)

  • C.

    Tia \(Ut\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)           

  • D.

    Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Us\)

Đáp án : A

Phương pháp giải :

Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.

Lời giải chi tiết :

Các cặp tia trùng nhau trong hình là: tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)

Vẽ đường thẳng $mn.$ Lấy điểm $O$ trên đường thẳng $mn,$ trên tia $Om$ lấy điểm $A,$ trên tia $On$ lấy điểm $B.$

Câu 14

Một cặp tia đối nhau gốc $O$  là:

  • A.

    \(OB,AO\)                 

  • B.

    \(mO,nO\)    

  • C.

    \(OA,Om\)     

  • D.

    \(OA,On\)

Đáp án : D

Phương pháp giải :

Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Lời giải chi tiết :

Các cặp tia đối nhau gốc \(O\) là: \(OA,OB\) (hoặc \(OA,On\) hoặc \(OB,Om\) hoặc \(Om,On\))

Câu 15

Một cặp tia đối nhau gốc $B$  là:

  • A.

    \(Bn,BA\)                  

  • B.

    \(BO,BA\) 

  • C.

    \(Bm,BA\)

  • D.

    \(OB,Bn\)

Đáp án : A

Phương pháp giải :

Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Lời giải chi tiết :

Các cặp tia đối nhau gốc \(B\) là: \(Bn,BO\) hoặc \(Bn,BA\) hoặc \(Bn,Bm\)

Câu 16

Có bao nhiêu cặp tia trùng nhau gốc \(O?\)

  • A.

    \(2\)

  • B.

    \(4\)    

  • C.

    \(3\)             

  • D.

    \(0\)

Đáp án : A

Phương pháp giải :

Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc

Lời giải chi tiết :

Các cặp tia trùng nhau gốc \(O\) là:

\(OA,Om\) và \(OB,On\)

Vậy có hai cặp tia trùng nhau gốc \(O\)

Câu 17

Trong ba điểm \(O;A;B\) thì điểm nào nằm giữa hai điểm còn lại?

  • A.

    \(A\)  

  • B.

    \(O\)    

  • C.

    \(B\)            

  • D.

    chưa kết luận được

Đáp án : B

Phương pháp giải :

Sử dụng chú ý sau: 
Nếu $Ax$ và $Ay$ là hai tia đối nhau, mà điểm $M$ thuộc tia $Ax,$ điểm $N$ thuộc tia $Ay$ thì điểm $A$ nằm giữa hai điểm $M$ và $N$

Lời giải chi tiết :

Vì điểm \(O\) nằm trên đường thẳng \(mn\) nên hai tia \(Om,On\) đối nhau.

Mà điểm \(A\) thuộc tia \(Om\) và điểm \(B\) thuộc tia \(On\) nên điểm \(O\) nằm giữa hai điểm \(A,B\)

Vẽ hai đường thẳng \(xy\) và \(mn\) cắt nhau tại \(O.\)

Câu 18

Kể tên các cặp tia đối nhau.

  • A.

    Không có cặp tia đối nhau                 

  • B.

    Cặp tia \(Ox,On\) và cặp tia \(Om,Oy\)

  • C.

    Cặp tia \(Ox,Oy\) và cặp tia \(Om,On\)                

  • D.

    Cặp tia \(Ox,Om\) và cặp tia \(Oy,On\)

Đáp án : C

Phương pháp giải :

Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Lời giải chi tiết :

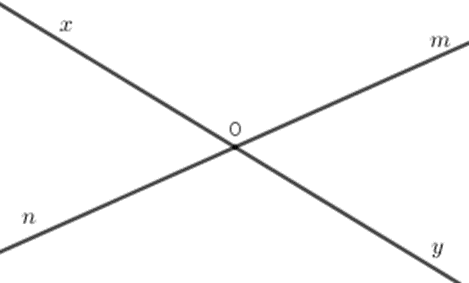Các cặp tia đối nhau là:\(Ox,Oy\) và \(Om,On\)

Câu 19

Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Kể tên các tia trùng nhau.

  • A.

    \(OA,On\) và \(OB,Om\) và \(Ox,Oy\)  

  • B.

    \(OA,On\) và \(OB,Om\)

  • C.

    \(OA,On\) và \(Ox,Oy\)         

  • D.

    \(OA,OB\) và \(OB,Om\)

Đáp án : B

Phương pháp giải :

Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc

Lời giải chi tiết :

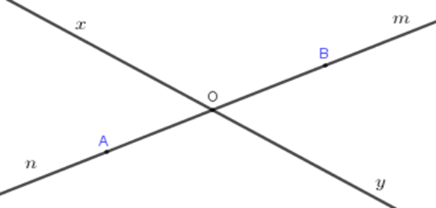Các cặp tia trùng nhau là: \(OA,On\) và \(OB,Om\)

Câu 20

Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Lấy điểm $C$ sao cho điểm \(O\) nằm giữa hai điểm \(B\) và \(C.\) Khi đó điểm \(C\) thuộc tia nào?

  • A.

    \(Ox,Oy\)                   

  • B.

    \(Oy,OA\)    

  • C.

    \(Om,OA\)     

  • D.

    \(On,OA\)

Đáp án : D

Phương pháp giải :

Nếu điểm \(O\) nằm giữa hai điểm\(A\) và \(B\) thì hai tia \(OA;OB\) đối nhau

Lời giải chi tiết :

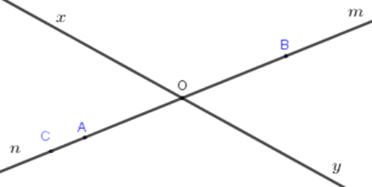Vì điểm \(O\) nằm giữa hai điểm \(B,C\) nên hai tia \(OB,OC\) đối nhau.

Nên \(C\) nằm trên tia đối của tia \(OB\) hay \(C\) nằm trên tia \(OA\) hoặc \(On\)

Cho hình vẽ sau

Câu 21

Tia nào trùng với tia $Ay$?

  • A.

    Tia $Ax$        

  • B.

    Tia $OB,By$

  • C.

    Tia $BA$       

  • D.

    Tia $AO,AB$

Đáp án : D

Phương pháp giải :

Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.

Lời giải chi tiết :

Có $2$ tia trùng với tia $Ay$ đó là tia $AO$ và tia $AB.$

Câu 22

Hai tia $Ax$ và $By$ có vị trí như thế nào với nhau

  • A.

    Đối nhau        

  • B.

    Trùng nhau

  • C.

    Không đối nhau, không trùng nhau   

  • D.

    Vừa đối nhau, vừa trùng nhau

Đáp án : C

Phương pháp giải :

Quan sát hình vẽ và nhận xét dựa vào gốc của hai tia \(Ax,By\)

Chú ý:

- Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.

- Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Lời giải chi tiết :

Hai tia $Ax$ và $By$ không chung gốc và nằm về hai phía khác nhau nên chúng không trùng nhau cũng không đối nhau .

Bài liên quan
close