Trắc nghiệm Bài 3: Phép trừ và phép chia Toán 6 Chân trời sáng tạoĐề bài
Câu 1 :
Phép tính \(x - 5\) thực hiện được khi
Câu 2 :
Cho phép tính \(231 - 87\). Chọn câu đúng.
Câu 3 :
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
Câu 4 :
Tính 1 454-997
Câu 5 :
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho: \(a = b.q + r\) Khẳng định nào sau đây đúng?
Câu 6 :
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
Câu 7 :
Trong các phép chia sau, có bao nhiêu phép chia có dư? 144:3 144:13 144:33 144:30
Câu 8 :
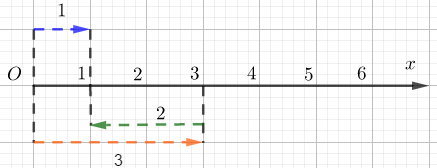
Hình ảnh sau minh họa cho phép toán nào?
Câu 9 :
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
Câu 10 :
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
Câu 11 :
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
Câu 12 :
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
Lời giải và đáp án
Câu 1 :
Phép tính \(x - 5\) thực hiện được khi
Đáp án : B Phương pháp giải :
Phép tính \(a - b\) thực hiện được khi \(a \ge b.\) Lời giải chi tiết :
Phép tính \(x - 5\) thực hiện được khi \(x \ge 5.\)
Câu 2 :
Cho phép tính \(231 - 87\). Chọn câu đúng.
Đáp án : C Phương pháp giải :
Trong phép trừ $a - b = x$ thì \(a\) là số bị trừ; \(b\) là số trừ và \(x\) là hiệu. Lời giải chi tiết :
Trong phép trừ \(231 - 87\) thì \(231\) là số bị trừ và \(87\) là số trừ nên C đúng.
Câu 3 :
Cho phép tính \(x:3 = 6\), khi đó thương của phép chia là
Đáp án : B Phương pháp giải :
Ta sử dụng (số bị chia) : (số chia) = (thương) để xác định thương của phép chia Lời giải chi tiết :
Phép chia \(x:3 = 6\) có \(x\) là số bị chia; \(3\) là số chia và \(6\) là thương. Nên thương của phép chia là \(6.\)
Câu 4 :
Tính 1 454-997
Đáp án : C Phương pháp giải :
- Thêm vào số bị trừ và số trừ cùng một số sao cho số trừ mới là số tròn chục, tròn trăm, tròn nghìn. - Tính: (số bị trừ mới) – (số trừ mới). Lời giải chi tiết :
1 454-997 = (1 454+3)-(997+3) = 1 457-1 000=457
Câu 5 :
Trong phép chia có dư \(a\) chia cho \(b,\) trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho: \(a = b.q + r\) Khẳng định nào sau đây đúng?
Đáp án : C Phương pháp giải :
Định nghĩa về phép chia hết và phép chia có dư. Lời giải chi tiết :
Khi chia a cho b, trong đó \(b \ne 0,\) ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho: \(a = b.q + r\) trong đó \(0 \le r < b\) Phép chia a cho b là phép chia có dư nên \(r \ne 0\) Vậy \(0 < r < b\).
Câu 6 :
Biểu diễn phép chia \(445:13\) dưới dạng \(a = b.q + r\) trong đó \(0 \le r < b\)
Đáp án : A Phương pháp giải :
Đặt tính rồi tính. Xác định a,b,q,r trong phép chia vừa nhận được. Lời giải chi tiết :
Số bị chia là \(b = 445\), số chia là \(b = 13\) thương \(q = 34\), số dư là \(r = 3\). Ta biểu diễn phép chia như sau: \(445 = 13.34 + 3\)
Câu 7 :
Trong các phép chia sau, có bao nhiêu phép chia có dư? 144:3 144:13 144:33 144:30
Đáp án : C Phương pháp giải :
Đặt tính rồi tính. Đếm số các phép chia có dư. Lời giải chi tiết :
Vậy có 3 phép chia có dư
Câu 8 :
Hình ảnh sau minh họa cho phép toán nào?
Đáp án : B Lời giải chi tiết :
Số 3 và số 1 cùng chiều từ trái sang phải, số 2 ngược chiều với hai số này. Mà ta có 3-2=1 nên hình ảnh trên minh họa cho phép trừ 3-2.
Câu 9 :
Dạng tổng quát của số tự nhiên chia hết cho \(3\) là:
Đáp án : A Phương pháp giải :
Sử dụng các số hạng chia hết cho \(a\) có dạng $x = a.k\,\left( {k \in N} \right)$ Lời giải chi tiết :
Các số hạng chia hết cho \(3\) có dạng tổng quát là \(x = 3k\,\left( {k \in N} \right)\)
Câu 10 :
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là
Đáp án : B Phương pháp giải :
Số tự nhiên \(a\) chia cho \(b\) được thương \(q\) và dư $r$ có dạng \(a = b.q + r.\) Lời giải chi tiết :
Dạng tổng quát của số tự nhiên chia cho \(5\) dư \(2\) là \(a = 5k + 2\,\left( {k \in N} \right).\)
Câu 11 :
Tình nhanh \(49.15 - 49.5\) ta được kết quả là
Đáp án : A Phương pháp giải :
Sử dụng tính chất phân phối của phép nhân với phép trừ \(ab - ac = a\left( {b - c} \right).\) Lời giải chi tiết :
Ta có \(49.15 - 49.5\)\( = 49.\left( {15 - 5} \right) = 49.10 = 490.\)
Câu 12 :
Kết quả của phép tính $12.100 + 100.36 - 100.19$ là
Đáp án : D Phương pháp giải :
Sử dụng tính chất phân phối của phép nhân với phép cộng; phép trừ \(ab + ac - ad = a\left( {b + d - c} \right).\) Lời giải chi tiết :
Ta có $12.100 + 100.36 - 100.19$\( = 100.\left( {12 + 36 - 19} \right) = 100.29 = 2900.\)
|
