Bài tập trắc nghiệm Toán 6 - Cánh diều

Trắc nghiệm Các dạng toán về tập hợp các số nguyên Toán 6 Cánh diều

Làm đề thi

Đề bài

Câu 1 :

Điểm cách \( - 1\) ba đơn vị theo chiều âm là

  • A

    $3$                         

  • B

    $ - 3$

  • C

    $ - 4$

  • D

    $4$

Câu 2 :

Những điểm cách điểm \(0\) ba đơn vị là

  • A

    $3$ và \( - 3\)

  • B

    $2$ và \( - 2\)  

  • C

    $2$ và \( - 3\)

  • D

    $3$ và \( - 2\)  

Câu 3 :

Những điểm cách  điểm 3 năm đơn vị là:

  • A

    $7$ và \( - 1\)

  • B

    $6$ và \( - 2\)

  • C

    $2$ và \( - 2\)

  • D

    $8$ và \( - 2\)  

Câu 4 :

Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:

  • A

    \( - 2; - 1\)  

  • B

    \( - 2; - 1;0;1\)

  • C

    \( - 3; - 2; - 1;0;1;2\)

  • D

    $0;1$

Câu 5 :

Có bao nhiêu  số nguyên nằm giữa \( - 3\) và \(4\) là:

  • A

    $3$                         

  • B

    $5$                            

  • C

    $6$

  • D

    $7$

Câu 6 :

Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?

  • A

    $3$

  • B

    $5$

  • C

    $2$

  • D

    $4$

Câu 7 :

Cách viết nào sau đây là đúng:

  • A
    \( - 2 \in \mathbb{N}\)
  • B
    \(1,5 \in \mathbb{Z}\)
  • C
    \( - 31 \in \mathbb{Z}\)
  • D
    \(1\dfrac{1}{2} \in \mathbb{Z}\)
Câu 8 : Các điểm E và F ở hình sau đây biểu diễn các số nguyên nào?

 

  • A
    \( - 3\) và \( - 5\)
  • B
    \( - 3\) và \( - 2\)
  • C
    \(1\) và \(2\)
  • D
    \( - 5\) và \( - 6\)
Câu 9 :

Cho trục số:

Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?

  • A
    \(4\)
  • B
    \( - 7\)
  • C
    \(7\)
  • D
    \(6\)
Câu 10 :

Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?

  • A
    1 số
  • B
    2 số
  • C
    3 số
  • D
    4 số
Câu 11 : Số đối của các số: \( - 3;\,\,12;\, - 82;\,\,29\) lần lượt là:
  • A
    \(3;\,\,12;\, - 82;\,\,29\)
  • B
    \( - 3;\,\, - 12;\, - 82;\, - \,29\)
  • C
    \(3;\,\,\,\,\,82;\,\,\, - 12;\,\,\, - 29\)
  • D
    \(3;\,\,\, - 12;\,\,\,82;\,\,\, - 29\)

Lời giải và đáp án

Câu 1 :

Điểm cách \( - 1\) ba đơn vị theo chiều âm là

  • A

    $3$                         

  • B

    $ - 3$

  • C

    $ - 4$

  • D

    $4$

Đáp án : C

Phương pháp giải :

- Sử dụng trục số để tìm đáp án

+ Trên trục số: Điểm \(0\) được gọi là điểm gốc của trục số. Chiều từ trái sang phải gọi là chiều dương (thường được đánh dấu bằng mũi tên), chiều từ phải sang trái gọi là chiều âm của trục số.

Lời giải chi tiết :

Điểm cách $ - 1$  ba đơn vị theo chiều âm là điểm nằm phía bên trái điểm $ - 1$  và cách điểm $ - 1$  ba đơn vị.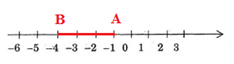

Điểm nằm bên trái điểm $ - 1$  và cách điểm $ - 1$  ba đơn vị là điểm $ - 4$
Nên điểm cách $ - 1$  ba đơn vị theo chiều âm là $ - 4.$     

Câu 2 :

Những điểm cách điểm \(0\) ba đơn vị là

  • A

    $3$ và \( - 3\)

  • B

    $2$ và \( - 2\)  

  • C

    $2$ và \( - 3\)

  • D

    $3$ và \( - 2\)  

Đáp án : A

Phương pháp giải :

Những điểm cách điểm $0$ ba đơn vị là điểm nằm bên phải điểm $0$  và cách điểm $0$  ba đơn vị, điểm nằm bên trái điểm $0$  và cách điểm $0$ ba đơn vị.

Lời giải chi tiết :

Điểm nằm bên phải điểm $0$ và cách điểm $0$ ba đơn vị là: $3$
Điểm nằm bên trái điểm $0$ và cách điểm $0$ ba đơn vị là: $ - 3$.

Câu 3 :

Những điểm cách  điểm 3 năm đơn vị là:

  • A

    $7$ và \( - 1\)

  • B

    $6$ và \( - 2\)

  • C

    $2$ và \( - 2\)

  • D

    $8$ và \( - 2\)  

Đáp án : D

Phương pháp giải :

Những điểm cách điểm $3$  năm đơn vị là điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị, điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị.

Lời giải chi tiết :

Điểm nằm bên phải điểm $3$ và cách điểm $3$ năm đơn vị là: $8$
Điểm nằm bên trái điểm $3$ và cách điểm $3$ năm đơn vị là: $ - 2$

Câu 4 :

Các số nguyên âm nằm giữa \( - 3\) và \(2\) là:

  • A

    \( - 2; - 1\)  

  • B

    \( - 2; - 1;0;1\)

  • C

    \( - 3; - 2; - 1;0;1;2\)

  • D

    $0;1$

Đáp án : A

Phương pháp giải :

+ Các số nằm giữa $ - 3$ và $2$ là các số nằm bên phải $ - 3$  và bên trái của $2$  trên trục số.

+ Chọn các số nguyên âm trong các số vừa tìm được

Lời giải chi tiết :

Các số nguyên nằm giữa $ - 3$ và $2$ là: \( - 2; - 1;0;1.\)

Các số nguyên âm nằm giữa $ - 3$ và $2$ là: \( - 2; - 1.\)

Câu 5 :

Có bao nhiêu  số nguyên nằm giữa \( - 3\) và \(4\) là:

  • A

    $3$                         

  • B

    $5$                            

  • C

    $6$

  • D

    $7$

Đáp án : C

Phương pháp giải :

Các số nằm giữa $ - 3$ và $4$ là các số nằm bên phải $ - 3$ và bên trái của $4$ trên trục số.

Lời giải chi tiết :

Các số nằm giữa $ - 3$ và $4$ là: \( - 2; - 1;0;1;2;3.\)

Vậy có \(6\) số thỏa mãn điều kiện đề bài.

Câu 6 :

Trên trục số điểm A cách gốc $4$ đơn vị về phía bên trái, điểm B cách gốc $1$ đơn vị về phía bên phải. Hỏi điểm A cách điểm B bao nhiêu đơn vị?

  • A

    $3$

  • B

    $5$

  • C

    $2$

  • D

    $4$

Đáp án : B

Phương pháp giải :

Dựa vào trục số để xác định.
Lưu ý: Gốc trên trục tọa độ là điểm $0.$

Lời giải chi tiết :

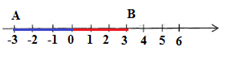
Quan sát trục số ta thấy:
Điểm cách gốc $4$ đơn vị vế phía bên trái là điểm $ - 4,$ nên điểm A biểu diễn số: $ - 4$
Điểm cách gốc $1$ đơn vị về phía bên phải là: $1$, nên điểm B biểu diễn số $1.$

Điểm $ - 4$ cách điểm $1$  là năm đơn vị.

Vậy điểm A cách điểm B là $5$ đơn vị.

Câu 7 :

Cách viết nào sau đây là đúng:

  • A
    \( - 2 \in \mathbb{N}\)
  • B
    \(1,5 \in \mathbb{Z}\)
  • C
    \( - 31 \in \mathbb{Z}\)
  • D
    \(1\dfrac{1}{2} \in \mathbb{Z}\)

Đáp án : C

Phương pháp giải :

\(\begin{array}{l}\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,...} \right\}\\\mathbb{Z} = \left\{ {...;\, - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\end{array}\)

Lời giải chi tiết :

\( - 2\) không là số tự nhiên => A sai.

\(1,5\) và \(1\dfrac{1}{2}\) không là số nguyên => B, D sai.

\( - 31\) là số nguyên => C đúng.

Câu 8 : Các điểm E và F ở hình sau đây biểu diễn các số nguyên nào?

 

  • A
    \( - 3\) và \( - 5\)
  • B
    \( - 3\) và \( - 2\)
  • C
    \(1\) và \(2\)
  • D
    \( - 5\) và \( - 6\)

Đáp án : B

Phương pháp giải :
Đếm khoảng cách từ điểm \(E;\,\,F\) đến điểm \(0\), thêm dấu “-” vào số vừa tìm được.
Lời giải chi tiết :
Các điểm E và F ở hình đã cho biểu diễn các số: \( - 3\) và \( - 2\).
Câu 9 :

Cho trục số:

Điểm \( - 4\) cách điểm \(3\) bao nhiêu đơn vị?

  • A
    \(4\)
  • B
    \( - 7\)
  • C
    \(7\)
  • D
    \(6\)

Đáp án : C

Phương pháp giải :

Đếm xem điểm \( - 4\) cách điểm \(3\) bao nhiêu khoảng, mỗi khoảng là 1 đơn vị.

Lời giải chi tiết :

Ta thấy điểm \( - 4\) cách điểm \(3\) bảy đơn vị.

Câu 10 :

Cho số nguyên \(a\), biết điểm \(a\) cách điểm \(0\) là \(6\) đơn vị. Có bao nhiêu số như vậy?

  • A
    1 số
  • B
    2 số
  • C
    3 số
  • D
    4 số

Đáp án : B

Phương pháp giải :
Quan sát trục số và tìm các điểm cách điểm \(0\) sáu đơn vị về chiều âm và về chiều dương
Lời giải chi tiết :
Có hai số cách điểm \(0\) sáu đơn vị đó là: \( - 6\) và \(6\).
Câu 11 : Số đối của các số: \( - 3;\,\,12;\, - 82;\,\,29\) lần lượt là:
  • A
    \(3;\,\,12;\, - 82;\,\,29\)
  • B
    \( - 3;\,\, - 12;\, - 82;\, - \,29\)
  • C
    \(3;\,\,\,\,\,82;\,\,\, - 12;\,\,\, - 29\)
  • D
    \(3;\,\,\, - 12;\,\,\,82;\,\,\, - 29\)

Đáp án : D

Phương pháp giải :

Số đối của số \(a\) là \( - a\).

Số đối của số \( - a\) là \(a\).

Lời giải chi tiết :
Số đối của các số: \( - 3;\,\,12;\, - 82;\,\,29\) lần lượt là: \(3;\,\,\, - 12;\,\,\,82;\,\,\, - 29\).
Bài liên quan
close