Trắc nghiệm Bài 4: Phép nhân, phép chia phân số Toán 6 Cánh diềuĐề bài
Câu 1 :
Chọn phát biểu đúng nhất trong các phát biểu sau:
Câu 2 :
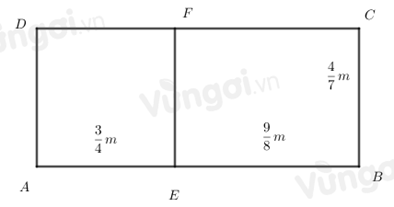
Tính diện tích hình chữ nhật ABCD ở hình sau:
Câu 3 :
Phép nhân phân số có những tính chất nào?
Câu 4 :
Tính: \(\dfrac{5}{8}\; \cdot \dfrac{{ - 3}}{4}\)
Câu 5 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \(\dfrac{{33}}{8}\) lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là cm
Câu 6 :
Kết quả của phép tính \(\left( { - 2} \right).\dfrac{3}{8}\) là
Câu 7 :
Chọn câu sai.
Câu 8 :
Tìm số nguyên \(x\) biết \(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\)
Câu 9 :
Tính \(\dfrac{9}{{14}} \cdot \dfrac{{ - 5}}{8} \cdot \dfrac{{14}}{9}\)
Câu 10 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\dfrac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là mét
Câu 11 :
Tìm \(x\) biết \(x:\left( { - \dfrac{2}{5}} \right) = \dfrac{3}{{54}}\)
Câu 12 :
Tính giá trị biểu thức $A = \left( {\dfrac{{11}}{4}.\dfrac{{ - 5}}{9} - \dfrac{4}{9}.\dfrac{{11}}{4}} \right).\dfrac{8}{{33}}$
Câu 13 :
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\dfrac{5}{3}\)cm và \(\dfrac{7}{4}\)cm?
Câu 14 :
Phân số nghịch đảo của phân số \(\dfrac{5}{6}\) là
Câu 15 :
Tính \(\dfrac{2}{3}:\dfrac{1}{2}\) bằng
Câu 16 :
Tìm \(x\) biết \(\dfrac{{13}}{{25}}:x = \dfrac{5}{{26}}\).
Câu 17 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một ô tô chạy hết \(\dfrac{3}{4}\) giờ trên một đoạn đường với vận tốc trung bình 40km/h. Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \(\dfrac{1}{2}\) giờ thì ô tô phải chạy với vận tốc trung bình là: \(km/h\)
Câu 18 :
Tính giá trị của biểu thức. \(\left( {\dfrac{{ - 2}}{{ - 5}}:\dfrac{3}{{ - 4}}} \right).\dfrac{4}{5}\)
Câu 19 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Bạn Hoà đã đọc hết một cuốn truyện dày 80 trang trong ba ngày. Biết ngày thứ nhất bạn Hoà đọc được \(\dfrac{3}{8}\) số trang cuốn truyện, ngày thứ hai đọc được \(\dfrac{2}{5}\) số trang cuốn truyện. Số trang bạn Hoà đã đọc được trong ngày thứ ba là trang Lời giải và đáp án
Câu 1 :
Chọn phát biểu đúng nhất trong các phát biểu sau:
Đáp án : D Lời giải chi tiết :
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. Phân số nào nhân với $1$ cũng bằng chính nó. Phân số nào nhân với $0$ cũng bằng $0$ Vậy cả A, B, C đều đúng.
Câu 2 :
Tính diện tích hình chữ nhật ABCD ở hình sau:
Đáp án : A Phương pháp giải :
- Cách 1: Tính chiều rộng của hình chữ nhật ABCD sau đó tính diện tích - Cách 2: Diện tích hình chữ nhật ABCD bằng tổng diện tích hai hình chữ nhật ADFE và BCFE. Lời giải chi tiết :
Cách 1: Chiều dài hình chữ nhật ABCD là: \(\dfrac{3}{4} + \dfrac{9}{8} = \dfrac{{15}}{8}\,(m)\) Diện tích hình chữ nhật ABCD là: \(\dfrac{4}{7}.\dfrac{{15}}{8} = \dfrac{{15}}{{14}}\) (m2) Cách 2: Diện tích hình chữ nhật ADFE là: \(\dfrac{3}{4}.\dfrac{4}{7} = \dfrac{3}{7}\)(m2) Diện tích hình chữ nhật BCFE là: \(\dfrac{4}{7}.\dfrac{9}{8} = \dfrac{9}{{14}}\) (m2) Diện tích hình chữ nhật ABCD là: \(\dfrac{3}{7} + \dfrac{9}{{14}} = \dfrac{{15}}{{14}}\) (m2)
Câu 3 :
Phép nhân phân số có những tính chất nào?
Đáp án : D Lời giải chi tiết :
Phép nhân phân số cũng có các tính chất tương tự phép nhân số tự nhiên như tính chất giao hoán, tính chất kết hợp, tính chất nhân phân phối.
Câu 4 :
Tính: \(\dfrac{5}{8}\; \cdot \dfrac{{ - 3}}{4}\)
Đáp án : C Phương pháp giải :
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số. Lời giải chi tiết :
\(\dfrac{5}{8}\; \cdot \dfrac{{ - 3}}{4} = \dfrac{{5.\left( { - 3} \right)}}{{8.4}} = \dfrac{{ - 15}}{{32}}\)
Câu 5 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \(\dfrac{{33}}{8}\) lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là cm Đáp án
Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \(\dfrac{{33}}{8}\) lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là cm Phương pháp giải :
Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ = \(\dfrac{{33}}{8}\). Chiều dài của chim ruồi ong. Lời giải chi tiết :
Chim ruồi ong hiện có chiều dài khoảng 5 cm. Chim ruồi "khổng lồ" ở Nam Mỹ dài gấp \(\dfrac{{33}}{8}\) lần chim ruồi ong. Chiều dài của chim ruồi "khổng lồ" ở Nam Mỹ là: \(\dfrac{{33}}{8}.5 = \dfrac{{33.5}}{8} = \dfrac{{165}}{8} = 20,625\)(cm).
Câu 6 :
Kết quả của phép tính \(\left( { - 2} \right).\dfrac{3}{8}\) là
Đáp án : D Phương pháp giải :
Muốn nhân một số nguyên với một phân số (hoặc một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu: \(a.\dfrac{b}{c} = \dfrac{{a.b}}{c}\) Chú ý rút gọn kết quả thu được. Lời giải chi tiết :
\(\left( { - 2} \right).\dfrac{3}{8} = \dfrac{{\left( { - 2} \right).3}}{8} = \dfrac{{ - 6}}{8} = \dfrac{{ - 3}}{4}\)
Câu 7 :
Chọn câu sai.
Đáp án : D Phương pháp giải :
Thực hiện các phép tính ở mỗi đáp án và tìm phép tính sai, sử dụng quy tắc nhân hai phân số: nhân tử với tử, mẫu với mẫu. Lời giải chi tiết :
Đáp án A: \(\dfrac{2}{7}.\dfrac{{14}}{6} = \dfrac{{2.14}}{{7.6}} = \dfrac{{28}}{{42}} = \dfrac{2}{3}\) nên A đúng. Đáp án B: \(25.\dfrac{{ - 4}}{{15}} = \dfrac{{25.\left( { - 4} \right)}}{{15}} = \dfrac{{ - 100}}{{15}} = \dfrac{{ - 20}}{3}\) nên B đúng. Đáp án C: \({\left( {\dfrac{2}{{ - 3}}} \right)^2}.\dfrac{9}{4} = \dfrac{{{2^2}}}{{{{\left( { - 3} \right)}^2}}}.\dfrac{9}{4}\)\( = \dfrac{4}{9}.\dfrac{9}{4} = 1\) nên C đúng. Đáp án D: \(\dfrac{{ - 16}}{{25}}.\left( {\dfrac{{25}}{{ - 24}}} \right) = \dfrac{{ - 16}}{{25}}.\dfrac{{25}}{{ - 24}}\)\( = \dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} \ne - \dfrac{2}{3}\) nên D sai.
Câu 8 :
Tìm số nguyên \(x\) biết \(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\)
Đáp án : A Phương pháp giải :
Thực hiện các phép tính ở hai vế rồi tìm \(x\) Chú ý: Muốn nhân hai phân số ta nhân tử với tử, mẫu với mẫu. Lời giải chi tiết :
\(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\) \(\dfrac{{ - 5}}{6}.\dfrac{{24}}{5} < x < \dfrac{{ - 1}}{5}.\dfrac{3}{2}\) \( - 4 < x < \dfrac{{ - 3}}{10}\) \(x \in \left\{ { - 3; - 2; - 1} \right\}\)
Câu 9 :
Tính \(\dfrac{9}{{14}} \cdot \dfrac{{ - 5}}{8} \cdot \dfrac{{14}}{9}\)
Đáp án : C Phương pháp giải :
Áp dụng tính chất giao hoán của phép nhân phân số để tính nhanh. +) Công thức tính nhanh: \(\dfrac{a}{b}.\dfrac{b}{a} = 1.\) Lời giải chi tiết :
\(\dfrac{9}{{14}} \cdot \dfrac{{ - 5}}{8} \cdot \dfrac{{14}}{9} = \left( {\dfrac{9}{{14}} \cdot \dfrac{{14}}{9}} \right) \cdot \dfrac{{ - 5}}{8} = 1.\dfrac{{ - 5}}{8} = \dfrac{{ - 5}}{8}.\)
Câu 10 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\dfrac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là mét Đáp án
Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \(\dfrac{5}{8}\) ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là mét Phương pháp giải :
Độ cao của đáy sông Sài Gòn = Độ cao của đáy vịnh Cam Ranh . \(\dfrac{5}{8}\) Lời giải chi tiết :
Độ cao của đáy sông Sài Gòn là: \( - 32.\dfrac{5}{8} = \dfrac{{ - 32.5}}{8} = - 20\) (mét)
Câu 11 :
Tìm \(x\) biết \(x:\left( { - \dfrac{2}{5}} \right) = \dfrac{3}{{54}}\)
Đáp án : D Phương pháp giải :
Muốn tìm số bị chia, ta lấy thương nhân với số chia. Lời giải chi tiết :
\(\begin{array}{l}x:\left( { - \dfrac{2}{5}} \right) = \dfrac{3}{{54}}\\x = \dfrac{3}{{54}}.\left( { - \dfrac{2}{5}} \right)\\x = \dfrac{1}{{18}}.\dfrac{{ - 2}}{5}\\x = \dfrac{{ - 1}}{{45}}\end{array}\)
Câu 12 :
Tính giá trị biểu thức $A = \left( {\dfrac{{11}}{4}.\dfrac{{ - 5}}{9} - \dfrac{4}{9}.\dfrac{{11}}{4}} \right).\dfrac{8}{{33}}$
Đáp án : A Phương pháp giải :
+ Tính trong ngoặc bằng cách sử dụng tính chất phân phối của phép nhân với phép trừ $ab - ac = a\left( {b - c} \right)$ + Thực hiện phép nhân hai phân số rồi rút gọn kết quả thu được. Lời giải chi tiết :
Ta có $A = \left( {\dfrac{{11}}{4}.\dfrac{{ - 5}}{9} - \dfrac{4}{9}.\dfrac{{11}}{4}} \right).\dfrac{8}{{33}}$ $ = \dfrac{{11}}{4}.\left( {\dfrac{{ - 5}}{9} - \dfrac{4}{9}} \right).\dfrac{8}{{33}} = \dfrac{{11}}{4}.\dfrac{{ - 9}}{9}.\dfrac{8}{{33}}$ $ = \dfrac{{ - 11}}{4}.\dfrac{8}{{33}} = \dfrac{{ - 2}}{3}$
Câu 13 :
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \(\dfrac{5}{3}\)cm và \(\dfrac{7}{4}\)cm?
Đáp án : C Phương pháp giải :
Áp dụng công thức xác định diện tích tam giác vuông: \(S = \dfrac{1}{2}a.b\) với \(a,b\) là hai cạnh góc vuông của tam giác vuông đó. Lời giải chi tiết :
Diện tích hình tam giác đó là: \(S = \dfrac{1}{2}.\dfrac{5}{3}.\dfrac{7}{4} = \dfrac{{1.5.7}}{{2.3.4}} = \dfrac{{35}}{{24}}\,c{m^2}\)
Câu 14 :
Phân số nghịch đảo của phân số \(\dfrac{5}{6}\) là
Đáp án : B Phương pháp giải :
+ Phân số nghịch đảo của \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\) Lời giải chi tiết :
Phân số nghịch đảo của phân số \(\dfrac{5}{6}\) là \(\dfrac{6}{5}\)
Câu 15 :
Tính \(\dfrac{2}{3}:\dfrac{1}{2}\) bằng
Đáp án : D Phương pháp giải :
Muốn chia hai phân số ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai. Lời giải chi tiết :
\(\dfrac{2}{3}:\dfrac{1}{2} = \dfrac{2}{3}.\dfrac{2}{1} = \dfrac{4}{3}\)
Câu 16 :
Tìm \(x\) biết \(\dfrac{{13}}{{25}}:x = \dfrac{5}{{26}}\).
Đáp án : B Phương pháp giải :
Xác định được rằng \(x\) là số chia nên ta tìm \(x\) bằng cách lấy số bị chia chia cho thương. Sử dụng qui tắc chia hai phân số để tìm ra kết quả. Lời giải chi tiết :
\(\begin{array}{l}\dfrac{{13}}{{25}}:x = \dfrac{5}{{26}}\\x = \dfrac{{13}}{{25}}:\dfrac{5}{{26}}\\x = \dfrac{{13}}{{25}}.\dfrac{{26}}{5}\\x = \dfrac{{338}}{{125}}\end{array}\)
Câu 17 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống: Một ô tô chạy hết \(\dfrac{3}{4}\) giờ trên một đoạn đường với vận tốc trung bình 40km/h. Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \(\dfrac{1}{2}\) giờ thì ô tô phải chạy với vận tốc trung bình là: \(km/h\) Đáp án
Một ô tô chạy hết \(\dfrac{3}{4}\) giờ trên một đoạn đường với vận tốc trung bình 40km/h. Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \(\dfrac{1}{2}\) giờ thì ô tô phải chạy với vận tốc trung bình là: \(km/h\) Phương pháp giải :
Công thức tính độ dài quãng đường: \(S = {v_{tb}}.t\) Công thức tính vận tốc trung bình: \({v_{tb}} = s:t\) Lời giải chi tiết :
Quãng đường ô tô đi được là: \(S = {v_{tb}}.t = 40.\dfrac{3}{4} = 30\,(km)\) Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \(\dfrac{1}{2}\) giờ thì ô tô phải chạy với vận tốc trung bình là: \({v_{tb}} = s:t = 30:\dfrac{1}{2} = 60\,\,\left( {km/h} \right)\)
Câu 18 :
Tính giá trị của biểu thức. \(\left( {\dfrac{{ - 2}}{{ - 5}}:\dfrac{3}{{ - 4}}} \right).\dfrac{4}{5}\)
Đáp án : C Phương pháp giải :
Tính theo thứ tự trong ngoặc trước, ngoài ngoặc sau. Lời giải chi tiết :
\(\begin{array}{l}\left( {\dfrac{{ - 2}}{{ - 5}}:\dfrac{3}{{ - 4}}} \right).\dfrac{4}{5} = \left( {\dfrac{2}{5}.\dfrac{{ - 4}}{3}} \right).\dfrac{4}{5}\\ = \dfrac{{ - 8}}{{15}}.\dfrac{4}{5} = \dfrac{{ - 32}}{{75}}\end{array}\)
Câu 19 : Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Điền số thích hợp vào ô trống Bạn Hoà đã đọc hết một cuốn truyện dày 80 trang trong ba ngày. Biết ngày thứ nhất bạn Hoà đọc được \(\dfrac{3}{8}\) số trang cuốn truyện, ngày thứ hai đọc được \(\dfrac{2}{5}\) số trang cuốn truyện. Số trang bạn Hoà đã đọc được trong ngày thứ ba là trang Đáp án
Bạn Hoà đã đọc hết một cuốn truyện dày 80 trang trong ba ngày. Biết ngày thứ nhất bạn Hoà đọc được \(\dfrac{3}{8}\) số trang cuốn truyện, ngày thứ hai đọc được \(\dfrac{2}{5}\) số trang cuốn truyện. Số trang bạn Hoà đã đọc được trong ngày thứ ba là trang Phương pháp giải :
- Tính số trang bạn Hòa đọc được trong ngày thứ nhất = tổng số trang . \(\dfrac{3}{8}\) - Tính số trang bạn Hòa đọc được trong ngày thứ hai = tổng số trang . \(\dfrac{2}{5}\) => Số trang bạn Hòa đọc được trong ngày thứ ba. Lời giải chi tiết :
Số trang bạn Hòa đọc được trong ngày thứ nhất là: 80.\(\dfrac{3}{8}\) = 30 (trang) Số trang bạn Hòa đọc được trong ngày thứ hai là: 80.\(\dfrac{2}{5}\) = 32 (trang) Số trang bạn Hòa đọc được trong ngày thứ ba là: 80 - 32 - 30 = 18 trang
|
