Trắc nghiệm Các dạng toán về phân tích một số ra thừa số nguyên tố Toán 6 Cánh diềuĐề bài
Câu 1 :
Khi phân tích các số \(2150;1490;2340\) ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố \(2;3\) và \(5?\)
Câu 2 :
Số 40 được phân tích thành các thừa số nguyên tố là:
Câu 3 :
Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố
Câu 4 :
225 chia hết cho tất cả bao nhiêu số nguyên tố?
Câu 5 :
Tích của hai số tự nhiên bằng \(105.\) Có bao nhiêu cặp số thỏa mãn?
Câu 6 :
Số $360$ khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
Câu 7 :
Số các ước của số $192$ là
Câu 8 :
Một hình vuông có diện tích là \(1936\,{m^2}.\) Tính cạnh của hình vuông đó.
Câu 9 :
Cho phép tính \(\overline {ab} .\,c\, = 424.\) Khi đó \(c\) bằng bao nhiêu?
Lời giải và đáp án
Câu 1 :
Khi phân tích các số \(2150;1490;2340\) ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố \(2;3\) và \(5?\)
Đáp án : A Phương pháp giải :
Sử dụng cách phân tích một số ra thừa số nguyên tố theo hàng dọc. Từ đó xét xem số nào được phân tích ra thừa số nguyên tố mà chứa cả các thừa số nguyên tố \(2;3\) và \(5.\) Lời giải chi tiết :
+) Phân tích số \(2150\) thành thừa số nguyên tố 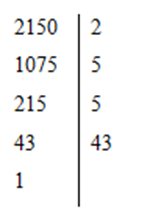 Suy ra \(2150 = {2.5^2}.43\) +) Phân tích số \(1490\) thành thừa số nguyên tố  Suy ra \(1490 = 2.5.149\) +) Phân tích số \(2340\) thành thừa số nguyên tố  Suy ra \(2340 = {2^2}{.3^2}.5.13\) Vậy có số \(2340\) thỏa mãn yêu cầu đề bài.
Câu 2 :
Số 40 được phân tích thành các thừa số nguyên tố là:
Đáp án : D Phương pháp giải :
Sử dụng phương pháp “rẽ nhánh”: - Tìm một ước nguyên tố của 40, là 2. - Viết 40 thành tích của 2 với một thừa số khác: 40=2.20. - Vẽ 2 nhánh từ số 40 cho hai số 2 và 20. - Tiếp tục tìm ước nguyên tố của 20, là 2. - Viết số 20 thành tích của 2 với một thừa số khác: 20=2.10. - Vẽ 2 nhánh từ số 20 cho hai số 2 và 10. - Viết số 10 thành tích của 2 với 5: 10=2.5 - Vẽ 2 nhánh từ số 10 cho hai số 2 và 5. - Hai số này đều là số nguyên tố nên ta dừng lại. - Lấy tích tất cả các thừa số ở cuối cùng mỗi nhánh. Lời giải chi tiết :
Vậy \(40 = 2.2.2.5 = {2^3}.5\)
Câu 3 :
Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố
Đáp án : B Phương pháp giải :
- Lấy 800 chia cho 400. Viết 800 thành tích của 400 và thương nhận được. - Viết 400 thành tích các thừa số nguyên tố. Lời giải chi tiết :
\(400 = {2^4}{.5^2}\) \(800 = 400.2 = {2.2^4}{.5^2} = {2^5}{.5^2}\)
Câu 4 :
225 chia hết cho tất cả bao nhiêu số nguyên tố?
Đáp án : D Phương pháp giải :
Phân tích các số ra thừa số nguyên tố theo cột dọc hoặc theo sơ đồ cây. Rồi liệt kê các ước nguyên tố của mỗi số. Lời giải chi tiết :
Số 225 chia hết cho các số nguyên tố: 3; 5 Vậy 225 chia hết cho 2 số nguyên tố.
Câu 5 :
Tích của hai số tự nhiên bằng \(105.\) Có bao nhiêu cặp số thỏa mãn?
Đáp án : D Phương pháp giải :
+ Phân tích số \(105\) ra thừa số nguyên tố. + Tìm các ước của \(105.\) Các số \(a;b\) chính là các ước của \(105\) sao cho tích của chúng bằng \(105.\) Lời giải chi tiết :
Gọi hai số tự nhiên cần tìm là \(a\) và \(b\left( {a;b \in N} \right)\) Ta có \(a.b = 105\) Phân tích số \(105\) ra thừa số nguyên tố ta được \(105 = 3.5.7\) Các số \(a;b\) là ước của \(105\) , do đó ta có 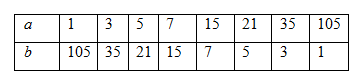 Vậy có \(8\) cặp số thỏa mãn yêu cầu.
Câu 6 :
Số $360$ khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
Đáp án : A Phương pháp giải :
- Phân tích số $360$ ra thừa số nguyên tố. - Đếm số lượng thừa số. Lời giải chi tiết :
Ta có  Nên \(360 = {2^3}{.3^2}.5\) Vậy có 3 thừa số nguyên tố sau khi phân tích là $2; 3$ và $5.$
Câu 7 :
Số các ước của số $192$ là
Đáp án : C Phương pháp giải :
- Phân tích số $192$ ra thừa số nguyên tố. - Tính các ước số bằng công thức: Cách tính số lượng các ước của một số \(m\,( m>1)\): ta xét dạng phân tích của số $m$ ra thừa số nguyên tố: Nếu \(m = a^x . b^y\) thì có ước \((x+1)(y+1)\)
Lời giải chi tiết :
Ta có 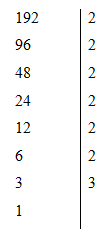 Nên \(192= 2^6 . 3\) nên số ước của $192$ là \((6+1)(1+1)=14\) ước.
Câu 8 :
Một hình vuông có diện tích là \(1936\,{m^2}.\) Tính cạnh của hình vuông đó.
Đáp án : A Phương pháp giải :
+ Phân tích số \(1936\) ra thừa số nguyên tố, từ đó phân tích thành tích các thừa số. + Dựa vào bốn cạnh hình vuông bằng nhau và diện tích hình vuông bằng cạnh nhân cạnh để tìm các thừa số phù hợp. Đó chính là độ dài cạnh hình vuông. Lời giải chi tiết :
Phân tích số \(1936\) ra thừa số nguyên tố ta được  Hay \(1936 = {2^4}{.11^2} = \left( {{2^2}.11} \right).\left( {{2^2}.11} \right) = 44.44\) Vậy cạnh hình vuông bằng \(44\,m.\)
Câu 9 :
Cho phép tính \(\overline {ab} .\,c\, = 424.\) Khi đó \(c\) bằng bao nhiêu?
Đáp án : B Phương pháp giải :
Phân tích số \(424\) ra thừa số nguyên tố, sau đó tìm các ước có hai chữ số và một chữ số của \(424\). Từ đó tìm được \(\overline {ab} \) và \(c.\) Lời giải chi tiết :
Vì \(\overline {ab} .\,c\, = 424\) nên \(\overline {ab} \) là ước có hai chữ số của \(424.\) Phân tích số \(424\) ra thừa số nguyên tố ta được  Hay \(424 = {2^3}.53\) Các ước của \(424\) là \(1;2;4;8;53;106;212;424\) Suy ra \(\overline {ab} = 53\) suy ra \(c = 424:53 = 8.\)
|
