Trắc nghiệm Các dạng toán về phép nhân, chia số nguyên, bội và ước của một số nguyên (tiếp) Toán 6 Kết nối tri thứcĐề bài
Câu 1 :
Tính nhanh $\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)$ ta được kết quả là
Câu 2 :
Giá trị biểu thức \(M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\) là
Câu 3 :
Tính hợp lý \(A = - 43.18 - 82.43 - 43.100\)
Câu 4 :
Cho $Q = - 135.17 - 121.17 - 256.\left( { - 17} \right)$, chọn câu đúng.
Câu 5 :
Tìm \(x \in Z\) biết \(\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\).
Câu 6 :
Có bao nhiêu ước của \( - 24.\)
Câu 7 :
Tìm $x,$ biết: $12\; \vdots \;x$ và $x < - 2$
Câu 8 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Câu 9 :
Tìm $x$ biết: \(25.x = - 225\)
Câu 10 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Câu 11 :
Giá trị nào dưới đây của \(x\) thỏa mãn \( - 6\left( {x + 7} \right) = 96?\)
Câu 12 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Câu 13 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Câu 14 :
Có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên biết: \(\left( {x - 1} \right)\left( {y + 1} \right) = 3?\)
Câu 15 :
Tìm số nguyên \(x\) thỏa mãn \({\left( { - 9} \right)^2}.x = 150 + 12.13x\)
Câu 16 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Câu 17 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Câu 18 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Câu 19 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Câu 20 :
Trong các phát biểu sau đây, phát biểu nào đúng?
Câu 21 :
Có bao nhiêu cách phân tích số 21 thành tích của hai số nguyên
Lời giải và đáp án
Câu 1 :
Tính nhanh $\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)$ ta được kết quả là
Đáp án : A Phương pháp giải :
Nhóm các cặp có tích là số tròn chục, tròn trăm, tròn nghìn... để tính nhanh. Lời giải chi tiết :
$\begin{array}{l}\left( { - 5} \right).125.\left( { - 8} \right).20.\left( { - 2} \right)\\ = \left[ {125.\left( { - 8} \right)} \right].\left[ {\left( { - 5} \right).20} \right].\left( { - 2} \right)\\ = - \left( {125.8} \right).\left[ { - \left( {5.20} \right)} \right].\left( { - 2} \right)\\ = \left( { - 1000} \right).\left( { - 100} \right).\left( { - 2} \right)\\ = 100000.\left( { - 2} \right) = - 200000\end{array}$
Câu 2 :
Giá trị biểu thức \(M = \left( { - 192873} \right).\left( { - 2345} \right).{\left( { - 4} \right)^5}.0\) là
Đáp án : C Phương pháp giải :
Áp dụng tính chất nhân một số với \(0\): Số nào nhân với \(0\) cũng bằng \(0\) Lời giải chi tiết :
Vì trong tích có một thừa số bằng \(0\) nên \(M = 0\)
Câu 3 :
Tính hợp lý \(A = - 43.18 - 82.43 - 43.100\)
Đáp án : C Phương pháp giải :
Sử dụng tính chất phân phối của phép nhân đối với phép trừ: $a.b - a.c = a.\left( {b - c} \right)$. Lời giải chi tiết :
\(\begin{array}{l}A = - 43.18 - 82.43 - 43.100\\A = 43.\left( { - 18 - 82 - 100} \right)\\A = 43.\left[ { - \left( {18 + 82 + 100} \right)} \right]\\A = 43.\left( { - 200} \right)\\A = - 8600\end{array}\)
Câu 4 :
Cho $Q = - 135.17 - 121.17 - 256.\left( { - 17} \right)$, chọn câu đúng.
Đáp án : B Phương pháp giải :
Sử dụng tính chất phân phối của phép nhân: $a.b - a.c - a.d = a.\left( {b - c - d} \right)$ Lời giải chi tiết :
$\begin{array}{l}Q = - 135.17 - 121.17 - 256.\left( { - 17} \right)\\Q = - 135.17 - 121.17 + 256.17\\Q = 17.\left( { - 135 - 121 + 256} \right)\\Q = 17.\left( { - 256 + 256} \right)\\Q = 17.0\\Q = 0\end{array}$
Câu 5 :
Tìm \(x \in Z\) biết \(\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\).
Đáp án : B Phương pháp giải :
- Sử dụng quy tắc bỏ ngoặc. - Nhóm \(x\) lại với nhau, nhóm số tự nhiên vào một nhóm. - Áp dụng công thức tổng các số cách đều nhau: Số số hạng = (Số cuối - số đầu):khoảng cách +1 Tổng = (Số cuối + số dầu).số số hạng :2 Lời giải chi tiết :
\(\begin{array}{l}\left( {x + 1} \right) + \left( {x + 2} \right) + ... + \left( {x + 99} \right) + \left( {x + 100} \right) = 0\\(x + x + .... + x) + (1 + 2 + ... + 100) = 0\\100{\rm{x}} + (100 + 1).100:2 = 0\\100{\rm{x}} + 5050 = 0\\100{\rm{x}} = - 5050\\x = - 50,5\end{array}\) Mà \(x\in Z\) nên không có $x$ thỏa mãn.
Câu 6 :
Có bao nhiêu ước của \( - 24.\)
Đáp án : D Phương pháp giải :
Để tìm tất cả các ước của một số nguyên âm ta chỉ cần tìm tất cả các ước của số đối của số nguyên âm đó. Trước tiên ta tìm ước tự nhiên rồi thêm các ước đối của chúng. Lời giải chi tiết :
Có \(8\) ước tự nhiên của \(24\) là: \(1;2;3;4;6;8;12;24\) Có \(8\) ước nguyên âm của \(24\) là: \(-1;-2;-3;-4;-6;-8;-12;-24\) Vậy có \(8.2 = 16\) ước của \( 24\) nên cũng có $16$ ước của $-24.$
Câu 7 :
Tìm $x,$ biết: $12\; \vdots \;x$ và $x < - 2$
Đáp án : B Phương pháp giải :
+ Bước 1: Tìm Ư$\left( {12} \right)$ Lời giải chi tiết :
Tập hợp ước của \(12\) là: \(A = \left\{ { \pm 1; \pm 2; \pm 3; \pm 4; \pm 6; \pm 12} \right\}\) Vì \(x < - 2\) nên \(x \in \left\{ { - 3; - 4; - 6; - 12} \right\}\)
Câu 8 :
Giá trị lớn nhất của $a$ thỏa mãn $a + 4$ là ước của $9$ là:
Đáp án : A Phương pháp giải :
+ Bước 1: Tìm ước của \(9\) Lời giải chi tiết :
$a + 4$ là ước của $9$ nên $\left( {a + 4} \right) \in Ư\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\;$  Vậy giá trị lớn nhất của \(a\) là \(a = 5\)
Câu 9 :
Tìm $x$ biết: \(25.x = - 225\)
Đáp án : C Phương pháp giải :
Tìm thừa số chưa biết trong một phép nhân: Ta lấy tích chia cho thừa số đã biết. Lời giải chi tiết :
\(\begin{array}{l}25.x = - 225\\x = - 225:25\\x = - 9\end{array}\)
Câu 10 :
Cho \(x \in \mathbb{Z}\) và \(\left( { - 154 + x} \right) \vdots \, 3\) thì:
Đáp án : A Phương pháp giải :
Sử dụng tính chất chia hết trong tập hợp các số nguyên $a \, \vdots \, m;b \, \vdots \, m \Rightarrow (a + b) \, \vdots \, m$ Lời giải chi tiết :
Ta có: \(\left( { - 154 + x} \right) \, \vdots \, 3\) \(\left( { - 153 - 1 + x} \right) \, \vdots \, 3\) Suy ra \(\left( {x - 1} \right) \, \vdots \, 3\) (do \( - 153 \, \vdots \, 3\)) Do đó \(x - 1 = 3k \Rightarrow x = 3k + 1\) Vậy \(x\) chia cho \(3\) dư \(1.\)
Câu 11 :
Giá trị nào dưới đây của \(x\) thỏa mãn \( - 6\left( {x + 7} \right) = 96?\)
Đáp án : C Lời giải chi tiết :
\(\begin{array}{l} - 6\left( {x + 7} \right) = 96\\x + 7 = 96:\left( { - 6} \right)\\x + 7 = - 16\\x = - 16 - 7\\x = - 23\end{array}\)
Câu 12 :
Tìm $n \in Z,$ biết: $\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$
Đáp án : B Phương pháp giải :
Bước 1: Phân tích $n + 5$ về dạng $a.\left( {n + 1} \right) + b{\rm{ }}\left( {a,b\; \in \;Z,a \ne 0} \right)$ Lời giải chi tiết :
$\left( {n{\rm{ }} + 5} \right) \vdots \left( {n{\rm{ }} + 1} \right)$$ \Rightarrow \left( {n + 1} \right) + 4 \, \vdots \, \left( {n{\rm{ }} + 1} \right)$ Vì \(n + 1 \, \vdots \, n + 1\) và \(n \in Z\) nên để \(n + 5 \, \vdots \, n + 1\) thì \(4 \, \vdots \, n + 1\) Hay \(n + 1 \in U\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\) Ta có bảng:  Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\)
Câu 13 :
Có bao nhiêu số nguyên $a < 5$ biết: $10$ là bội của $\left( {2a + 5} \right)$
Đáp án : A Phương pháp giải :
\(10\) là bội của \(2a + 5\) nghĩa là \(2a + 5\) là ước của \(10\) - Tìm các ước của \(10\) - Lập bảng tìm \(a,\) đối chiếu điều kiện và kết luận. Lời giải chi tiết :
Vì \(10\) là bội của \(2a + 5\) nên \(2a + 5\) là ước của \(10\) \(U\left( {10} \right) = \left\{ { \pm 1; \pm 2; \pm 5; \pm 10} \right\}\) Ta có bảng: 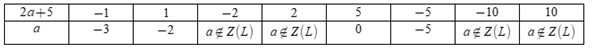 Mà \(a < 5\) nên \(a \in \left\{ { - 3; - 2;0; - 5} \right\}\) Vậy có \(4\) giá trị nguyên của \(a\) thỏa mãn bài toán.
Câu 14 :
Có bao nhiêu cặp số \(\left( {x;y} \right)\) nguyên biết: \(\left( {x - 1} \right)\left( {y + 1} \right) = 3?\)
Đáp án : D Phương pháp giải :
- Tìm các cặp số có tích bằng \(3\) - Lập bảng tìm các giá trị của \(x,y\) và kết luận. Lời giải chi tiết :
Ta có: \(3 = 1.3 = 3.1 = \left( { - 1} \right).\left( { - 3} \right) = \left( { - 3} \right).\left( { - 1} \right)\) Ta có bảng: 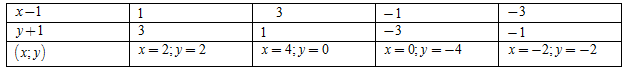 Vậy có \(4\) cặp số \(\left( {x;y} \right)\) thỏa mãn là: \(\left( {2;2} \right),\left( {4;0} \right),\left( {0; - 4} \right),\left( { - 2; - 2} \right)\)
Câu 15 :
Tìm số nguyên \(x\) thỏa mãn \({\left( { - 9} \right)^2}.x = 150 + 12.13x\)
Đáp án : B Phương pháp giải :
- Thực hiện các phép tính, thu gọn biểu thức - Tìm x Lời giải chi tiết :
\(\begin{array}{l}{\left( { - 9} \right)^2}.x = 150 + 12.13x\\81x = 150 + 156x\\81x - 156x = 150\\ - 75x = 150\\x = 150:\left( { - 75} \right)\\x = - 2\end{array}\)
Câu 16 :
Cho \(a\) và \(b\) là hai số nguyên khác \(0.\) Biết \(a \, \vdots \, b\) và \(b \, \vdots \, a.\) Khi đó
Đáp án : D Phương pháp giải :
Sử dụng định nghĩa chia hết: \(a \, \vdots \, b\) nếu và chỉ nếu tồn tại số \(q \in Z\) sao cho \(a = b.q\) Lời giải chi tiết :
Ta có: \(\begin{array}{l}a \, \vdots \, b \Rightarrow a = b.{q_1}\left( {{q_1} \in Z} \right)\\b \, \vdots \, a \Rightarrow b = a.{q_2}\left( {{q_2} \in Z} \right)\end{array}\) Suy ra \(a = b.{q_1} = \left( {a.{q_2}} \right).{q_1} = a.\left( {{q_1}{q_2}} \right)\) Vì \(a \ne 0\) nên \(a = a\left( {{q_1}{q_2}} \right) \Rightarrow 1 = {q_1}{q_2}\) Mà \({q_1},{q_2} \in Z\) nên \({q_1} = {q_2} = 1\) hoặc \({q_1} = {q_2} = - 1\) Do đó \(a = b\) hoặc \(a = - b\)
Câu 17 :
Gọi \(A\) là tập hợp các giá trị $n \in Z$ để \(\left( {{n^2} - 7} \right)\) là bội của \(\left( {n + 3} \right)\). Tổng các phần tử của \(A\) bằng:
Đáp án : A Phương pháp giải :
Biến đổi biểu thức \({n^2} - 7\) về dạng \(a.\left( {n + 3} \right) + b\) với \(b \in Z\) rồi suy ra \(n + 3\) là ước của \(b\) Lời giải chi tiết :
Ta có:\({n^2} - 7 = {n^2} + 3n - 3n - 9 + 2\)\( = n\left( {n + 3} \right) - 3\left( {n + 3} \right) + 2\)\( = \left( {n - 3} \right)\left( {n + 3} \right) + 2\) Vì \(n \in Z\) nên để \({n^2} - 7\) là bội của \(n + 3\) thì \(2\) là bội của \(n + 3\) hay \(n + 3\) là ước của \(2\) \(Ư\left( 2 \right) = \left\{ { \pm 1; \pm 2} \right\}\) nên \(n + 3 \in \left\{ { \pm 1; \pm 2} \right\}\) Ta có bảng:  Vậy \(n \in A = \left\{ { - 5; - 4; - 2; - 1} \right\}\) Do đó tổng các phần tử của \(A\) là \(\left( { - 5} \right) + \left( { - 4} \right) + \left( { - 2} \right) + \left( { - 1} \right) = - 12\)
Câu 18 :
Cho \(x;\,y \in \mathbb{Z}\). Nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) chia hết cho
Đáp án : C Phương pháp giải :
+ Biến đổi để tách \(5x + 46y\) thành tổng của hai số, trong đó một số chia hết cho $16$ và một số chứa nhân tử \(x + 6y\) + Sử dụng tính chất chia hết trên tập hợp các số nguyên để chứng minh. Lời giải chi tiết :
Ta có: \(\begin{array}{l}5x + 46y = 5x + 30y + 16y\\ = \left( {5x + 30y} \right) + 16y\\ = 5\left( {x + 6y} \right) + 16y\end{array}\) Vì \(5x + 46y\) chia hết cho $16$ và $16y$ chia hết cho $16$ nên suy ra \(5\left( {x + 6y} \right)\) chia hết cho $16.$ Mà $5$ không chia hết cho $16$ nên suy ra \(x + 6y\) chia hết cho $16$ Vậy nếu \(5x + 46y\) chia hết cho $16$ thì \(x + 6y\) cũng chia hết cho $16.$
Câu 19 :
Có bao nhiêu số nguyên \(n\) thỏa mãn \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(\left( {n - 1} \right)?\)
Đáp án : C Phương pháp giải :
Áp dụng: \(b\) chia hết cho \(a\) và \(a\) chia hết cho \(b\) thì \(a\),\(b\) là hai số đối nhau (đã chứng minh từ bài tập trước), từ đó suy ra \(n\). Lời giải chi tiết :
Vì \(\left( {n - 1} \right)\) là bội của \(\left( {n + 5} \right)\) và \(\left( {n + 5} \right)\) là bội của \(n - 1\), Nên \(n - 1\) khác \(0\) và \(n + 5\) khác \(0\) Nên \(n + 5,n - 1\) là hai số đối nhau Do đó: \((n + 5) + (n - 1) = 0\) \(2n + 5 - 1 = 0\) \(2n + 4 = 0\) \(2n = -4\) \(n=-2\) Vậy có 1 số nguyên n thỏa mãn bài toán.
Câu 20 :
Trong các phát biểu sau đây, phát biểu nào đúng?
Đáp án : C Phương pháp giải :
Cho \(a,b \in \mathbb{Z}\) và \(b \ne 0\). Nếu có số nguyên \(q\) sao cho \(a = bq\) thì: Ta nói \(a\) chia hết cho \(b\), kí hiệu là \(a \vdots b\). Lời giải chi tiết :
Ta có: \( - 18 = \left( { - 6} \right).3\) nên \( - 18\) chia hết cho \( - 6\) => C đúng
Câu 21 :
Có bao nhiêu cách phân tích số 21 thành tích của hai số nguyên
Đáp án : C Phương pháp giải :
- Phân tích số 21 thành tích của hai số nguyên dương - Suy ra các cách phân tích khác nhờ đổi dấu hai thừa số Lời giải chi tiết :
Ta có hai cách phân tích 21 thành tích hai số nguyên dương là: \(21 = 3.7 = 1.21\) Từ đó suy ra các 2 cách phân tích khác nhờ đổi dấu hai thừa số: \(21 = \left( { - 3} \right).\left( { - 7} \right) = \left( { - 1} \right).\left( { - 21} \right)\) Vậy ta có bốn cách phân tích.
|
