Trắc nghiệm Tổng hợp bài tập dao động cơ (phần 2) - Vật Lí 12Đề bài
Câu 1 :
Một con lắc đơn gồm một vật nhỏ khối lượng \(m = 2g\) và một dây treo mảnh, chiều dài \(l\) , được kích thích cho dao động điều hòa, Trong khoảng thời gian Δt con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn \(7,9cm\) thì cũng trong khoảng thời gian Δt con lắc thực hiện được \(39\) dao động. Lấy gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}9,8m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc chiều dài \(l\), người ta truyền cho vật điện tích \(q{\rm{ }} = {\rm{ }} + {\rm{ }}{0,5.10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Vecto cường độ điện trường này có
Câu 2 :
Một con lắc đơn có chiều dài \(1{\rm{ }}m\), đầu trên cố định đầu dưới gắn với vật nặng có khối lượng m. Điểm cố định cách mặt đất \(2,5{\rm{ }}m\). Ở thời điểm ban đầu đưa con lắc lệch khỏi vị trí cân bằng một góc \(a = {\rm{ }}0,09{\rm{ }}rad\), rồi thả nhẹ khi con lắc vừa qua vị trí cân bằng thì sợi dây bị đứt. Bỏ qua mọi sức cản, lấy \(g{\rm{ }} = {\rm{ }}9,8{\rm{ }}m/{s^2}\). Tốc độ của vật nặng ở thời điểm \(t{\rm{ }} = {\rm{ }}0,08{\rm{ }}s\) có giá trị gần bằng:
Câu 3 :
Một con lắc gồm lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) một đầu cố định, đầu kia gắn với một vật nhỏ khối lượng \({m_1} = {\rm{ }}m\) đặt trên mặt phẳng nằm ngang không ma sát. Ban đầu kéo lò xo dãn một đoạn \(10cm\) rồi buông nhẹ để $m$ dao động điều hòa. Ở thời điểm lò xo có chiều dài cực tiểu, ta đặt nhẹ vật \({m_2} = {\rm{ }}3m\) lên trên \({m_1}\), sau đó cả hai cùng dao động điều hòa với vận tốc cực đại \(50\sqrt 2 cm/s\) . Giá trị của $m$ là:
Câu 4 :
Một lò xo độ cứng \(k = 50{\rm{ }}N/m\), một đầu cố định, đầu còn lại treo vật nặng khối lượng \(m = 100g\). Điểm treo lò xo chịu được lực tối đa không quá \(4N\). Lấy \(g = 10m/{s^2}\). Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá:
Câu 5 :
Một con lắc đơn gồm một vật nhỏ có khối lượng \(m = 2{\rm{ }}g\) và một dây treo mảnh, chiều dài \(l\), được kích thích cho dao động điều hòa. Trong khoảng thời gian \(\Delta t\) con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn bằng \(7,9cm\), thì cũng trong khoảng thời gian $Δt$ con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường \(g = 9,8{\rm{ }}m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc có chiều dài \(l\), người ta truyền cho vật điện tích \(q = - {10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Véc tơ cường độ điện trường này có
Câu 6 :
Trong thang máy, tại trần người ta treo một con lắc lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}25{\rm{ }}N/m\), vật nặng có khối lượng \(400{\rm{ }}g\). Khi thang máy đứng yên ta cho con lắc dao động điều hòa, chiều dài con lắc thay đổi từ \(32{\rm{ }}cm\) đến \(48{\rm{ }}cm\). Tại thời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc \(a = \dfrac{g}{{10}}\) . Lấy \(g = {\pi ^2}m/{s^2} = 10{\rm{ }}m/{s^2}\). Biên độ dao động của vật trong trường hợp này là:
Câu 7 :
Một con lắc đơn gồm sợi dây mảnh dài \(l = 1m\), vật có khối lượng \(m = 100\sqrt 3 g\) tích điện \(q = {10^{ - 5}}\left( C \right)\). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường \(\overrightarrow g \) và có độ lớn \(E = {10^5}V/m\). Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo của con lắc và \(\overrightarrow g \) bằng \({60^0}\) rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là:
Câu 8 :
Một vật nhỏ có khối lượng \(M = 0,9{\rm{ }}kg\), gắn trên một lò xo nhẹ thẳng đứng có độ cứng \(25{\rm{ }}N/m\) đầu dưới của lò xo cố định. Một vật nhỏ có khối lượng \(m = 0,1{\rm{ }}kg\) chuyển động theo phương thẳng đứng với tốc độ \(2\sqrt 2 m/s\) đến va chạm mềm với $M$. Sau va chạm hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Biên độ dao động là:
Câu 9 :
Hai con lắc lò xo giống nhau treo vào hai điểm trên cùng giá đỡ nằm ngang. Chọn trục tọa độ Ox có phương thẳng đứng, chiều từ trên xuống dưới. Phương trình dao động của hai con lắc là \({x_1} = 3\cos \left( {10\sqrt 3 t} \right)cm\) và \({x_2} = 4\cos (10\sqrt 3 t + \dfrac{\pi }{2})cm\)(t tính bằng s). Biết lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\), gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Hợp lực do hai con lắc tác dụng lên giá đỡ trong quá trình dao động có độ lớn cực đại là:
Câu 10 :
Một con lắc lò xo treo thẳng gồm vật nhỏ khối lượng \(m{\rm{ }} = {\rm{ }}1{\rm{ }}kg\), lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}100{\rm{ }}N/m\). Đặt một giá nằm ngang đỡ vật m để lò xo có chiều dài tự nhiên rồi cho giá đỡ chuyển động thẳng đứng xuống nhanh dần đều không vận tốc đầu với gia tốc \(a{\rm{ }} = {\rm{ }}2{\rm{ }}m/{s^2}\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Sau khi rời giá đỡ thì vật m dao động điều hòa với biên độ:
Câu 11 :
Một lò xo nhẹ làm bằng vật liệu cách điện có độ cứng k = 50N/m, một đầu được gắn cố định, đầu còn lại gắn vào quả cầu nhỏ tích điện q = 5µC, khối lượng m = 50g. Quả cầu có thể dao động không ma sát dọc theo trục lò xo nằm ngang và cách điện. Tại thời điểm ban đầu t = 0 kéo vật tới vị trí lò xo dãn 4 cm rồi thả nhẹ đến thời điểm t = 0,1 s thì thiết lập điện trường không đổi trong thời gian 0,1 s, biết điện trường nằm ngang dọc theo trục lò xo hướng ra xa điểm cố định và có độ lớn E = 105 V/m. Lấy g = 10 m/s2, π2 = 10 . Trong quá trình dao động thì tốc độ cực đại mà quả cầu đạt được gần nhất giá trị nào sau đây?
Câu 12 :
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 25N/m một đầu được gắn với hòn bi nhỏ có khối lượng 100g. Tại thời điểm t = 0, thả cho con lắc rơi tự do sao cho trục của lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm \({t_1} = 0,02\sqrt {30} \,s\) thì đầu trên của lò xo bị giữ lại đột ngột. Sau đó vật dao động điều hòa. Lấy g = 10m/s2. Tại thời điểm \({t_2} = {t_1} + 0,1\,\left( s \right)\), tốc độ của hòn bi gần giá trị nào sau đây?
Câu 13 :
Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc α, có \(\tan \alpha = \dfrac{3}{4}\); lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
Câu 14 :
Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm trường ngoại lực có độ lớn F theo phương ngang. Nếu quay phương của ngoại lực một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là \({T_1} = 2,5\,\,s\) hoặc \({T_2} = 1,6\,\,s\). Chu kì T gần nhất giá trị nào sau đây?
Câu 15 :
Cho một con lắc dao động tắt dần chậm trong môi trường có ma sát. Nếu sau mỗi chu kì cơ năng của con lắc giảm 5% thì sau 10 chu kì biên độ của nó giảm xấp xỉ
Câu 16 :
Một vật hình trụ tiết diện nhỏ, có chiều cao \(20\;{\rm{cm}}\), nổi thẳng đứng trong một bể nước rộng. Bỏ qua mọi lực cản, lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\). Khi cân bằng, một nửa vật bị chìm trong nước và mép dưới của vật cách đáy bể một đoạn đủ dài. Từ vị trí cân bằng của vật, truyền cho nó vận tốc ban đầu bằng \(1,5\;{\rm{m}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Kể từ lúc vật bắt đầu chuyển động đến lúc vận tốc của vật triệt tiêu lần đầu tiên thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?
Câu 17 :
Đề thi THPT QG - 2020 Cho hệ vật gồm lò xo nhẹ có độ cứng k = 20 N/m, vật M có khối lượng 30 g được nối với vật N có khối lượng 150 g bằng một sợi dây không dãn vắt qua ròng rọc như hình bên. Bỏ qua mọi ma sát, bỏ qua khối lượng dây và ròng rọc. Ban đầu giữ M tại vị trí để lò xo không biến dạng, N ở xa mặt đất. Thả nhẹ M để cả hai vật cùng chuyển động, sau 0,2 s thì dây bị đứt. Sau khi dây đứt, M dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Lấy \(g = 10m/{s^2},{\mkern 1mu} {\mkern 1mu} ({\pi ^2} \approx 10).\) Giá trị của A bằng
Lời giải và đáp án
Câu 1 :
Một con lắc đơn gồm một vật nhỏ khối lượng \(m = 2g\) và một dây treo mảnh, chiều dài \(l\) , được kích thích cho dao động điều hòa, Trong khoảng thời gian Δt con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn \(7,9cm\) thì cũng trong khoảng thời gian Δt con lắc thực hiện được \(39\) dao động. Lấy gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}9,8m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc chiều dài \(l\), người ta truyền cho vật điện tích \(q{\rm{ }} = {\rm{ }} + {\rm{ }}{0,5.10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Vecto cường độ điện trường này có
Đáp án : D Phương pháp giải :
+ Sử dụng công thức tính chu kì của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) + Sử dụng lí thuyết về bài toán con lắc đơn chịu tác dụng của lực điện trường. Lời giải chi tiết :
\(\begin{array}{l}T = 2\pi \sqrt {\dfrac{l}{g}} = \dfrac{{\Delta t}}{N}\\ \Rightarrow \left\{ \begin{array}{l}{T_1} = 2\pi \sqrt {\dfrac{{{l_1}}}{g}} = \dfrac{{\Delta t}}{{40}}\\{T_2} = 2\pi \sqrt {\dfrac{{{l_2}}}{g}} = \dfrac{{\Delta t}}{{39}}\end{array} \right.\\ \Rightarrow \dfrac{{{T_1}}}{{{T_2}}} = \dfrac{{39}}{{40}} = \sqrt {\dfrac{{{l_1}}}{{{l_2}}}} = \sqrt {\dfrac{{{l_1}}}{{{l_1} + 7,9}}} \\ \Rightarrow {l_1} = 152,1cm;{l_2} = 160cm\\{T_1} = {T_3} \Leftrightarrow 2\pi \sqrt {\dfrac{{152,1}}{g}} = 2\pi \sqrt {\dfrac{{160}}{{g'}}} \\ \Rightarrow g' = g \pm a = 10,31\\ \Rightarrow a = 0,51 = \dfrac{{{F_d}}}{m} = \dfrac{{qE}}{m}\\ \Rightarrow E = 2,{04.10^5}\left( {V/m} \right)\end{array}\) Để $\overrightarrow a ,\overrightarrow g $ cùng hướng, \(q{\rm{ }} > {\rm{ }}0\) thì \(\overrightarrow E \) hướng xuống
Câu 2 :
Một con lắc đơn có chiều dài \(1{\rm{ }}m\), đầu trên cố định đầu dưới gắn với vật nặng có khối lượng m. Điểm cố định cách mặt đất \(2,5{\rm{ }}m\). Ở thời điểm ban đầu đưa con lắc lệch khỏi vị trí cân bằng một góc \(a = {\rm{ }}0,09{\rm{ }}rad\), rồi thả nhẹ khi con lắc vừa qua vị trí cân bằng thì sợi dây bị đứt. Bỏ qua mọi sức cản, lấy \(g{\rm{ }} = {\rm{ }}9,8{\rm{ }}m/{s^2}\). Tốc độ của vật nặng ở thời điểm \(t{\rm{ }} = {\rm{ }}0,08{\rm{ }}s\) có giá trị gần bằng:
Đáp án : D Phương pháp giải :
+ Sử dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) + Sử dụng trục thời gian + Vận dụng biểu thức tính vận tốc của con lắc đơn: \({v^2} = 2g\left( {{\rm{cos}}\alpha {\rm{ - cos}}{\alpha _0}} \right)\) Lời giải chi tiết :
Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\frac{l}{g}} = 2s \Rightarrow \omega = \pi \left( {rad/s} \right)\) Thời điểm sợi dây treo con lắc bị đứt là t0 = T/4 = 0,5s Vậy thời điểm t = 0,08s con lắc chưa bị đứt. PT dao động của con lắc: \(\alpha = {\alpha _0}\cos \pi t\) Khi t = 0,08s thì α = 0,087 rad Tốc độ của vật nặng khi đó: \(v = \sqrt {2.9,8.\left( {\cos 0,0872 - \cos 0,09} \right)} = 0,069m/s\)
Câu 3 :
Một con lắc gồm lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\) một đầu cố định, đầu kia gắn với một vật nhỏ khối lượng \({m_1} = {\rm{ }}m\) đặt trên mặt phẳng nằm ngang không ma sát. Ban đầu kéo lò xo dãn một đoạn \(10cm\) rồi buông nhẹ để $m$ dao động điều hòa. Ở thời điểm lò xo có chiều dài cực tiểu, ta đặt nhẹ vật \({m_2} = {\rm{ }}3m\) lên trên \({m_1}\), sau đó cả hai cùng dao động điều hòa với vận tốc cực đại \(50\sqrt 2 cm/s\) . Giá trị của $m$ là:
Đáp án : A Phương pháp giải :
+ Sử dụng công thức tính vận tốc cực đại của vật dao động điều hoà: \({v_{{\rm{max}}}} = \omega A\) + Sử dụng công thức tính tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \) Lời giải chi tiết :
 => Sau đó hệ sẽ dao động với biên độ \(A' = A = 10cm\) + Vận tốc cực đại của con lắc sau đó là \(v{'_{\max }} = \omega 'A' = \omega 'A \Rightarrow \omega {'^2} = \dfrac{k}{{4m}} = {\left( {\dfrac{{{v_{\max }}}}{A}} \right)^2}\) Do đó khối lượng m là: $m = \dfrac{{k{A^2}}}{{4v_{max}^2}} = \dfrac{{50.0,{1^2}}}{{4.0,{5^2}.2}} = 0,25kg$
Câu 4 :
Một lò xo độ cứng \(k = 50{\rm{ }}N/m\), một đầu cố định, đầu còn lại treo vật nặng khối lượng \(m = 100g\). Điểm treo lò xo chịu được lực tối đa không quá \(4N\). Lấy \(g = 10m/{s^2}\). Để hệ thống không bị rơi thì vật nặng dao động theo phương thẳng đứng với biên độ không quá:
Đáp án : D Phương pháp giải :
+ Sử dụng biểu thức tính tần số góc của con lắc lò xo: \(\omega = \sqrt {\frac{k}{m}} \) + Sử dụng biểu thức tính độ dãn của lò xo treo thẳng đứng: \(\Delta l = \frac{{mg}}{k}\) + Vận dụng biểu thức tính lực đàn hồi: \({F_{dh}} = kA\) Lời giải chi tiết :
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = 10\sqrt 5 \left( {rad/s} \right)\) + Độ giãn của lò xo ở VTCB: \(\Delta {l_0} = \frac{{mg}}{k} = 0,02m\) + Điểm treo của con lắc chịu được lực tối đa không quá \(4N \to {F_{dhmax}} \le {\rm{ }}4N\) \( \Leftrightarrow k\left( {\Delta {l_0} + A} \right) \le 4 \Rightarrow A \le \frac{{4 - k\Delta {l_0}}}{k} = \frac{{4 - 50.0,02}}{{50}} = 0,06m = 6cm\)
Câu 5 :
Một con lắc đơn gồm một vật nhỏ có khối lượng \(m = 2{\rm{ }}g\) và một dây treo mảnh, chiều dài \(l\), được kích thích cho dao động điều hòa. Trong khoảng thời gian \(\Delta t\) con lắc thực hiện được \(40\) dao động. Khi tăng chiều dài con lắc thêm một đoạn bằng \(7,9cm\), thì cũng trong khoảng thời gian $Δt$ con lắc thực hiện được 39 dao động. Lấy gia tốc trọng trường \(g = 9,8{\rm{ }}m/{s^2}\). Để con lắc với chiều dài tăng thêm có cùng chu kỳ dao động với con lắc có chiều dài \(l\), người ta truyền cho vật điện tích \(q = - {10^{ - 8}}C\) rồi cho nó dao động điều hòa trong một điện trường đều có đường sức thẳng đứng. Véc tơ cường độ điện trường này có
Đáp án : B Phương pháp giải :
+ Sử dụng công thức tính chu kì của con lắc đơn \(\omega = \sqrt {\dfrac{k}{m}} = 5\sqrt 2 (rad/s)\) + Sử dụng lí thuyết về con lắc chịu tác dụng của lực điện trường. Lời giải chi tiết :
+ Chiều dài của con lắc là $l$. Khi chiều dài là $l$ → chu kì dao động \(T = \dfrac{{\Delta t}}{{40}}\) Khi chiều dài là $l+ 7,9cm$ → chu kì dao động \(T' = \dfrac{{\Delta t}}{{39}}\) \( \Rightarrow \dfrac{l}{{l + 7,9}} = \dfrac{{{T^2}}}{{T{'^2}}} = \dfrac{{{{39}^2}}}{{{{40}^2}}} \Rightarrow l = 152,1cm\) + Con lắc có chiều dài tăng thêm là $l’ = l + 7,9 cm = 160 cm$, tích thêm điện tích \(q{\text{ }} = {\text{ }} - {10^{ - 8}}C\) Theo đề bài: \(T' = T \Leftrightarrow \sqrt {\dfrac{{l'}}{{g'}}} = \sqrt {\dfrac{l}{g}} \Rightarrow g' = g.\dfrac{{l'}}{g} = 9,8.\dfrac{{160}}{{152,1}} = 10,31m/{s^2}\) Nhận xét: \(g' > g\) mà \(\overrightarrow {g'} = \overrightarrow g + \dfrac{{\overrightarrow F }}{m} \Rightarrow \overrightarrow F \uparrow \uparrow \overrightarrow g \) mà \(q < 0 \Rightarrow \overrightarrow E \uparrow \downarrow \overrightarrow g \) hay \(\overrightarrow E \) thẳng đứng hướng lên. Và: \(\begin{array}{l}\dfrac{{\left| q \right|E}}{m} = g' - g\\ \Rightarrow E = \dfrac{{\left( {g' - g} \right).m}}{{\left| q \right|}} = \dfrac{{\left( {10,31 - 9,8} \right){{.2.10}^{ - 3}}}}{{{{10}^{ - 8}}}}\\ = 102000V/m = 1,{02.10^5}V/m\end{array}\)
Câu 6 :
Trong thang máy, tại trần người ta treo một con lắc lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}25{\rm{ }}N/m\), vật nặng có khối lượng \(400{\rm{ }}g\). Khi thang máy đứng yên ta cho con lắc dao động điều hòa, chiều dài con lắc thay đổi từ \(32{\rm{ }}cm\) đến \(48{\rm{ }}cm\). Tại thời điểm mà vật ở vị trí thấp nhất thì cho thang máy đi xuống nhanh dần đều với gia tốc \(a = \dfrac{g}{{10}}\) . Lấy \(g = {\pi ^2}m/{s^2} = 10{\rm{ }}m/{s^2}\). Biên độ dao động của vật trong trường hợp này là:
Đáp án : B Phương pháp giải :
+ Sử dụng công thức tính tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \) + Sử dụng công thức tính biên độ theo chiều dài max – min: \(A = \dfrac{{{l_{{\rm{max}}}} - {l_{\min }}}}{2}\) + Sử dụng công thức tính lực quán tính: \(F = ma\) + Vận dụng hệ thức độc lập A – x – v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
- Khi thang máy chưa chuyển động + Tần số góc: $\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{25}}{{0,4}}} = 2,5\pi \left( {rad/s} \right)$ + Biên đô dao động: $A = \dfrac{{{l_{{\text{max}}}} - {l_{\min }}}}{2} = \dfrac{{48 - 32}}{2} = 8cm$ - Khi thang máy chuyển động nhanh dần đều đi xuống thì con lắc chịu thêm tác dụng của lực quán tính $\overrightarrow {{F_q}} $ hướng lên, có độ lớn ${F_q} = ma = \dfrac{{mg}}{{10}}$ => VTCB mới là: \({\text{O}}{{\text{O}}_1} = \dfrac{{{F_q}}}{k} = \dfrac{{mg}}{{10k}} = 0,016m = 1,6cm\) => Khi đó so với VTCB vật đang ở li độ \({x_1} = {\rm{ }}A{\rm{ }} + {\rm{ }}1,6{\rm{ }} = {\rm{ }}9,6{\rm{ }}cm\), vân tốc \({v_1} = {\rm{ }}v{\rm{ }} = {\rm{ }}0\) => Biên độ dao động mới là ${A_1} = \sqrt {x_1^2 + \dfrac{{v_1^2}}{{{\omega ^2}}}} = {x_1} = 9,6cm$
Câu 7 :
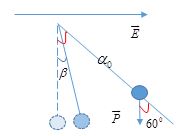
Một con lắc đơn gồm sợi dây mảnh dài \(l = 1m\), vật có khối lượng \(m = 100\sqrt 3 g\) tích điện \(q = {10^{ - 5}}\left( C \right)\). Treo con lắc đơn trong điện trường đều có phương vuông góc với gia tốc trọng trường \(\overrightarrow g \) và có độ lớn \(E = {10^5}V/m\). Kéo vật theo chiều của vec tơ điện trường sao cho góc tạo bởi dây treo của con lắc và \(\overrightarrow g \) bằng \({60^0}\) rồi thả nhẹ để vật dao động. Lực căng cực đại của dây treo là:
Đáp án : C Phương pháp giải :
+ Vận dụng biểu thức tính lực điện: \({F_d} = qE\) + Sử dụng công thức tính lực căng dây cực đại: \({T_{{\rm{max}}}} = mg\left( {3 - 2\cos {\alpha _0}} \right)\) Lời giải chi tiết :
+ VTCB mới của con lắc là vị trí mà dây treo hợp với phương thẳng đứng góc \(\beta \) sao cho: \(\tan \beta = \dfrac{{\left| q \right|E}}{{mg}} = \dfrac{{{{10}^{ - 5}}{{.10}^5}}}{{100\sqrt 3 {{.10}^{ - 3}}.10}} = \dfrac{1}{{\sqrt 3 }} \Rightarrow \beta = {30^0}\left( {rad} \right)\) + Kéo con lắc đơn ra sao cho gia tốc trọng trường \(g\) tạo với dây treo của con lắc một góc ${60^0}$ => CLĐ sẽ dao động với biên độ \({\alpha _0} = {60^0}{\text{ - }}\beta = {60^0} - {30^0} = {30^0}\). + Gia tốc trọng trường hiệu dụng \(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + {g^2}{{\tan }^2}\beta } = \dfrac{{2g}}{{\sqrt 3 }}\) Lực căng dây cực đại của con lắc đơn: \({T_{\max }} = mg'\left( {3 - 2\cos {\alpha _0}} \right) = 100\sqrt 3 {.10^{ - 3}}.\dfrac{{2.10}}{{\sqrt 3 }}.\left( {3 - 2\cos {{30}^0}} \right) = 2,54N\)
Câu 8 :
Một vật nhỏ có khối lượng \(M = 0,9{\rm{ }}kg\), gắn trên một lò xo nhẹ thẳng đứng có độ cứng \(25{\rm{ }}N/m\) đầu dưới của lò xo cố định. Một vật nhỏ có khối lượng \(m = 0,1{\rm{ }}kg\) chuyển động theo phương thẳng đứng với tốc độ \(2\sqrt 2 m/s\) đến va chạm mềm với $M$. Sau va chạm hai vật dính vào nhau và cùng dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Biên độ dao động là:
Đáp án : C Phương pháp giải :
Bài toán va chạm mềm của con lắc lò xo + Sử dụng lí thuyết về dao động điều hòa của con lắc lò xo: - Độ dãn của con lắc lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\) - Biểu thức tính tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \) - Hệ thức độc lập A – x – v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) + Định luật bảo toàn động lượng: \(\overrightarrow p = \overrightarrow {p'} \) Lời giải chi tiết :
+ Theo ĐL bảo toàn động lượng: \(\begin{array}{l}m{v_0} = \left( {M + m} \right)v\\ \Rightarrow v = \dfrac{{m{v_0}}}{{M + m}} = \dfrac{{0,1.2\sqrt 2 }}{{0,9 + 0,1}}\\ = 0,2\sqrt 2 \left( {m/s} \right) = 20\sqrt 2 cm/s\end{array}\) + Xét con lắc lò xo trước và sau khi va chạm : 
Câu 9 :
Hai con lắc lò xo giống nhau treo vào hai điểm trên cùng giá đỡ nằm ngang. Chọn trục tọa độ Ox có phương thẳng đứng, chiều từ trên xuống dưới. Phương trình dao động của hai con lắc là \({x_1} = 3\cos \left( {10\sqrt 3 t} \right)cm\) và \({x_2} = 4\cos (10\sqrt 3 t + \dfrac{\pi }{2})cm\)(t tính bằng s). Biết lò xo có độ cứng \(k{\rm{ }} = {\rm{ }}50{\rm{ }}N/m\), gia tốc trọng trường \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Hợp lực do hai con lắc tác dụng lên giá đỡ trong quá trình dao động có độ lớn cực đại là:
Đáp án : A Phương pháp giải :
Vận dụng lí thuyết về lực đàn hồi trong dao động của con lắc lò xo thẳng đứng Lời giải chi tiết :
ADCT: $\begin{array}{l}{\omega ^2} = \dfrac{g}{{\Delta {l_0}}}\\ \Rightarrow \Delta {l_0} = \dfrac{g}{{{\omega ^2}}} = \dfrac{{10}}{{{{\left( {10\sqrt 3 } \right)}^2}}} = \dfrac{1}{{30}}m\end{array}$ Lực tác dụng vào điểm treo chính là lực đàn hồi của lò xo, lực này trực đối với lực đàn hồi tác dụng vào vật nên: ${\overrightarrow {F'} _{dh1}} = - {\overrightarrow F _{dh1}};{\overrightarrow {F'} _{dh2}} = - {\overrightarrow F _{dh2}}$ $\begin{array}{l}F = {F_{dh1}} + {F_{dh2}} = k\left( {\Delta {l_0} + {x_1}} \right) + k\left( {\Delta {l_0} + {x_2}} \right) = 2k\Delta {l_0} + k\left( {{x_1} + {x_2}} \right)\\ = 2.50.\dfrac{1}{{30}} + 50\left[ {0,03.\cos \left( {10\sqrt 3 t} \right) + 0,04.\cos \left( {10\sqrt 3 t + \dfrac{\pi }{2}} \right)} \right]\\ \Rightarrow F = 2.50.\dfrac{1}{{30}} + 50\left[ {0,05\cos \left( {10\sqrt 3 t + 0,094} \right)} \right]\\ \Rightarrow {F_{\max }} = 2.50.\dfrac{1}{{30}} + 50.0,05 \approx 5,833N\end{array}$
Câu 10 :
Một con lắc lò xo treo thẳng gồm vật nhỏ khối lượng \(m{\rm{ }} = {\rm{ }}1{\rm{ }}kg\), lò xo nhẹ có độ cứng \(k{\rm{ }} = {\rm{ }}100{\rm{ }}N/m\). Đặt một giá nằm ngang đỡ vật m để lò xo có chiều dài tự nhiên rồi cho giá đỡ chuyển động thẳng đứng xuống nhanh dần đều không vận tốc đầu với gia tốc \(a{\rm{ }} = {\rm{ }}2{\rm{ }}m/{s^2}\). Lấy \(g{\rm{ }} = {\rm{ }}10{\rm{ }}m/{s^2}\). Sau khi rời giá đỡ thì vật m dao động điều hòa với biên độ:
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức định luật II – Niuton: \(\overrightarrow F = m\overrightarrow a \) + Sử dụng biểu thức tính độ dãn của con lắc lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\) + Sử dụng biểu thức tính tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \) + Sử dụng hệ thức độc lập A – x – v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
+ Khi cho giá đỡ chuyển động thì các lực tác dụng vào vật nặng của con lắc Trọng lực, lực đàn hồi, phản lực do giá đỡ tác dụng lên vật Theo định luật II Niu-tơn ta có: \(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_{dh}}} = m\overrightarrow a \) Chiếu lên chiều dương là chiều chuyển động đi xuống của vật ta có: \(P - N - {F_{dh}} = ma \Rightarrow N = P - {F_{dh}} - ma\) + Giá đỡ rời vật khi \(N{\rm{ }} = {\rm{ }}0\) \( \Rightarrow P - {F_{dh}} - ma =0\Rightarrow {F_{dh}} = P - ma \Leftrightarrow \Delta l = \dfrac{{m(g - a)}}{k} = 0,08(m)\) Hay giá đỡ rời vật khi lò xo giãn đoạn \(8{\rm{ }}cm\) , mà độ giãn của lò xo ở VTCB \(\Delta {l_0} = \dfrac{{mg}}{k} = 10cm\) => Vật đang ở vị trí có li độ \(x{\rm{ }} = {\rm{ }} - {\rm{ }}2{\rm{ }}cm\) + Vận tốc của vật tại vị trí đó là \(v = \sqrt {2as} = \sqrt {2a\Delta l} = 40\sqrt 2 (cm/s)\) + Tần số góc \(\omega = \sqrt {\dfrac{k}{m}} = 10(rad/s)\) => Vật sẽ dao động với biên độ \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{( - 2)}^2} + \dfrac{{{{40}^2}.2}}{{{{10}^2}}}} = 6(cm)\)
Câu 11 :
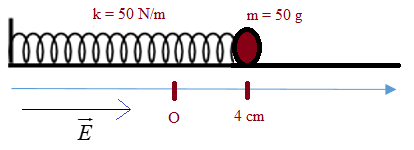
Một lò xo nhẹ làm bằng vật liệu cách điện có độ cứng k = 50N/m, một đầu được gắn cố định, đầu còn lại gắn vào quả cầu nhỏ tích điện q = 5µC, khối lượng m = 50g. Quả cầu có thể dao động không ma sát dọc theo trục lò xo nằm ngang và cách điện. Tại thời điểm ban đầu t = 0 kéo vật tới vị trí lò xo dãn 4 cm rồi thả nhẹ đến thời điểm t = 0,1 s thì thiết lập điện trường không đổi trong thời gian 0,1 s, biết điện trường nằm ngang dọc theo trục lò xo hướng ra xa điểm cố định và có độ lớn E = 105 V/m. Lấy g = 10 m/s2, π2 = 10 . Trong quá trình dao động thì tốc độ cực đại mà quả cầu đạt được gần nhất giá trị nào sau đây?
Đáp án : C Phương pháp giải :
+ Xác định tần số góc, và chu kì dao động ban đầu của hệ dao động. Xác định vị trí của vật mà ta thiết lập điện trường \(\overrightarrow E \). + Khi đó, vật chịu tác dụng của lực điện, vì q > 0 nên lực điện cùng chiều \(\overrightarrow E \). Vị trí cân bằng của vật lúc này thay đổi một đoạn ∆l0với \(F = q.E = k.\Delta {l_0}\) Do đó vật dao động với biên độ mới. Áp dụng công thức xác định tần số góc và chu kì: \(\omega = \sqrt {\frac{k}{m}} ;T = \frac{{2\pi }}{\omega }\) Vận tốc cực đại mới là: \({v_{\max }}' = \omega .A'\) Lời giải chi tiết :
Ta có hình vẽ:
Tần số góc và chu kì: \(\left\{ \begin{array}{l} Ban đầu kéo vật khỏi vị trí cân bằng 4cm, rồi thả nhẹ thì vật dao động với biên độ A = 4cm, chu kì T = 0,2s. Sau khi chuyển động được 0,1s vật đi đến vị trí biên âm. Ta thiết lập điện trường E thì vật chịu tác dụng của lực điện trường \(\overrightarrow F = q.\overrightarrow E \) do đó vị trí cân bằng bị thay đổi ∆l0 với: \(F = q.E = k.\Delta {l_0} \Rightarrow \Delta {l_0} = \frac{{{{5.10}^{ - 6}}{{.10}^5}}}{{50}} = 0,01m = 1cm\) Biên độ dao động mới: \(A' = A + \Delta {l_0}\; = 4 + 1 = 5cm\) Sau khoảng thời gian \(\Delta t = 0,5T = 0,1{\rm{s}}\) con lắc đến vị trí biên dương (lò xo giãn 6cm), điện trường bị mất đi) => vị trí cân bằng của con lắc lại trở về vị trí lò xo không biến dạng => con lắc sẽ dao động với biên độ \({A_3} = 6cm\) Vận tốc cực đại mới là: \({v_{\max }} = \omega .{A_3} = 10\pi .6 = 188,5cm/s\) Vậy giá trị gần nhất là 190 cm/s
Câu 12 :
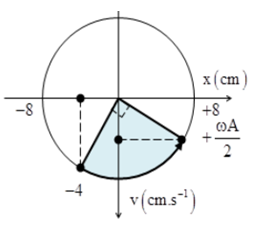
Một con lắc lò xo gồm lò xo nhẹ có độ cứng 25N/m một đầu được gắn với hòn bi nhỏ có khối lượng 100g. Tại thời điểm t = 0, thả cho con lắc rơi tự do sao cho trục của lò xo luôn nằm theo phương thẳng đứng và vật nặng ở phía dưới lò xo. Đến thời điểm \({t_1} = 0,02\sqrt {30} \,s\) thì đầu trên của lò xo bị giữ lại đột ngột. Sau đó vật dao động điều hòa. Lấy g = 10m/s2. Tại thời điểm \({t_2} = {t_1} + 0,1\,\left( s \right)\), tốc độ của hòn bi gần giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} \Rightarrow T = \dfrac{{2\pi }}{\omega }\) Vận tốc của vật rơi tự do: \(v = g.t\) Độ giãn của lò xo tại VTCB: \(\Delta {l_0} = \dfrac{{mg}}{k}\) Biên độ dao động: \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} \) Sử dụng VTLG tính ra được tốc độ của vật tại t2. Lời giải chi tiết :
Tần số góc: \(\omega = \sqrt {\dfrac{k}{m}} = \sqrt {\dfrac{{25}}{{0,1}}} = 5\pi \,\left( {rad/s} \right) \Rightarrow T = 0,4s\) Khi thả rơi tự do con lắc thì nó ở trạng thái không biến dạng và vận tốc của nó tại thời điểm \({t_1} = 0,02\sqrt {30} \,s\)là: \(v = gt = 10.0,02\sqrt {30} = 0,2\sqrt {30} m/s\) Sau khi đột ngột giữ lại đầu trên của con lắc thì con lắc sẽ dao động quanh vị trí cân bằng. Tại vị trí này lò xo giãn: \(\Delta {l_0} = \dfrac{{mg}}{k} = \dfrac{{0,1.10}}{{25}} = 0,04m = 4cm\) Chọn trục tọa độ thẳng đứng chiều dương hướng xuống dưới, gốc tọa độ tại VTCB thì li độ của lò xo tại thời điểm lò xo bị giữ là: \(x = - \Delta {l_0} = - 4cm\) Biên độ dao động của con lắc: \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( { - 0,04} \right)}^2} + \dfrac{{{{\left( {0,2\sqrt {30} } \right)}^2}}}{{{{\left( {5\pi } \right)}^2}}}} = 8cm\) Thời điểm \({t_2} = {t_1} + 0,1\,\left( s \right) = {t_1} + \dfrac{T}{4} \Rightarrow \Delta t = \dfrac{T}{4}\) Biểu diễn trên VTLG ta có: Từ VTLG ta có: \(v = \dfrac{{\omega A}}{2} = \dfrac{{5\pi .8}}{2} = 20\pi \approx 62,8cm/s\) Chọn A.
Câu 13 :
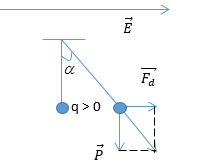
Một con lắc đơn gồm hòn bi nhỏ bằng kim loại được tích điện q > 0. Khi đặt con lắc vào trong điện trường đều có véc tơ cường độ điện trường nằm ngang thì tại vị trí cân bằng dây treo hợp với phương thẳng đứng một góc α, có \(\tan \alpha = \dfrac{3}{4}\); lúc này con lắc dao động nhỏ với chu kỳ T1. Nếu đổi chiều điện trường này sao cho véctơ cường độ diện trường có phương thẳng đứng hướng lên và cường độ không đổi thì chu kỳ dao động nhỏ của con lắc lúc này là:
Đáp án : D Phương pháp giải :
\(\begin{array}{l}\overrightarrow {{F_d}} = q.\overrightarrow E = m.\overrightarrow a \\\overrightarrow {{F_d}} \bot \overrightarrow P \Rightarrow g' = \sqrt {{g^2} + {a^2}} \\\overrightarrow {{F_d}} \uparrow \uparrow \overrightarrow P \Rightarrow g' = g + a\\\overrightarrow {{F_d}} \uparrow \downarrow \overrightarrow P \Rightarrow g' = g - a\\T = 2\pi \sqrt {\dfrac{l}{{g'}}} \end{array}\) Lời giải chi tiết :
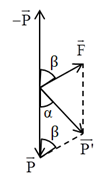
Khi vecto cường độ điện trường nằm ngang: Từ hình vẽ ta có: \(\tan \alpha = \dfrac{{{F_d}}}{P} = \dfrac{{ma}}{{mg}} = \dfrac{3}{4} \Rightarrow a = \dfrac{3}{4}.g\) Gia tốc trọng trường hiệu dụng : \(g' = \sqrt {{g^2} + {a^2}} = \sqrt {{g^2} + \dfrac{{9{g^2}}}{{16}}} = \dfrac{5}{4}.g\) Chu kì dao động của con lắc khi đó: \({T_1} = 2\pi \sqrt {\dfrac{l}{{g'}}} = \dfrac{2}{{\sqrt 5 }}.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\left( 1 \right)\) + Khi đổi chiều điện trường sao cho hướng vecto cường độ điện trường hướng lên thì \(\overrightarrow {{F_d}} \) hướng lên (do q > 0). Gia tốc trọng trường hiệu dụng khi đó: \(g'' = g - a = g - \dfrac{3}{4}.g = \dfrac{1}{4}.g\) Chu kì dao động của con lắc khi đó: \({T_2} = 2\pi \sqrt {\dfrac{l}{{g''}}} = 2.2\pi \sqrt {\dfrac{l}{g}} \,\,\,\,\,\left( 2 \right)\) + Từ (1) và (2) ta có: \(\dfrac{{{T_2}}}{{{T_1}}} = \sqrt 5 \Rightarrow {T_2} = \sqrt 5 .{T_1}\)
Câu 14 :
Một con lắc đơn dao động điều hòa với chu kì T tại nơi có thêm trường ngoại lực có độ lớn F theo phương ngang. Nếu quay phương của ngoại lực một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) trong mặt phẳng thẳng đứng và giữ nguyên độ lớn thì chu kì dao động là \({T_1} = 2,5\,\,s\) hoặc \({T_2} = 1,6\,\,s\). Chu kì T gần nhất giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Gia tốc hiệu dụng của con lắc khi ngoại lực hướng theo phương ngang: \({g_0} = \sqrt {{g^2} + {a^2}} \) Gia tốc hiệu dụng của con lắc khi ngoại lực hợp với phương thẳng đứng góc β: \(g' = \sqrt {{g^2} + {a^2} - 2g.a.cos\beta } \) Chu kì của con lắc đơn: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \) Lời giải chi tiết :
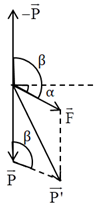
Nhận xét: \(T = 2\pi \sqrt {\dfrac{{\rm{l}}}{g}} \Rightarrow {T^2} = 4{\pi ^2}\dfrac{{\rm{l}}}{g} \Rightarrow {T^2} \sim \dfrac{1}{g}\) hay \(g \sim \dfrac{1}{{{T^2}}}\) Ban đầu \(\overrightarrow F \) theo phương ngang, gia tốc hiệu dụng: \({g_0} = \sqrt {{g^2} + {a^2}} \) Trường hợp 1: \(\overrightarrow F \) hướng lên trên: Ta có: \(\beta = {90^0} - \alpha \Rightarrow \cos \beta = - \sin \alpha \) Gia tốc hiệu dụng là: \({g_1} = \sqrt {{g^2} + {a^2} + 2g.a.\sin \alpha } \) \( \Rightarrow {g_1}^2 = {g^2} + {a^2} + 2g.a.\sin \alpha \,\,\left( 1 \right)\) Trường hợp 2: \(\overrightarrow F \) hướng xuống dưới: Ta có: \(\beta = {90^0} + \alpha \Rightarrow \cos \beta = \sin \alpha \) Gia tốc hiệu dụng là: \({g_2} = \sqrt {{g^2} + {a^2} - 2g.a.\sin \alpha } \) \( \Rightarrow {g_2}^2 = {g^2} + {a^2} - 2g.a.\sin \alpha \,\,\left( 2 \right)\) Từ (1) và (2) ta có: \({g_1}^2 + {g_2}^2 = 2\left( {{g^2} + {a^2}} \right)\) \( \Rightarrow \dfrac{1}{{{T_1}^4}} + \dfrac{1}{{{T_2}^4}} = \dfrac{2}{{{T_0}^4}} \Rightarrow \dfrac{1}{{2,{5^4}}} + \dfrac{1}{{1,{6^4}}} = \dfrac{2}{{{T_0}^4}} \Rightarrow {T_0} \approx 1,83\,\,\left( s \right)\)
Câu 15 :
Cho một con lắc dao động tắt dần chậm trong môi trường có ma sát. Nếu sau mỗi chu kì cơ năng của con lắc giảm 5% thì sau 10 chu kì biên độ của nó giảm xấp xỉ
Đáp án : C Phương pháp giải :
Cơ năng của con lắc: \({\rm{W}} = \frac{1}{2}.k.{A^2}\) Cơ năng con lắc sau 1 chu kì còn: \({{\rm{W}}_1} = (100\% - 5\% ).{{\rm{W}}_0} \Rightarrow {{\rm{W}}_n} = {(100\% - 5\% )^n}.{{\rm{W}}_0}\) (với n là số chu kì) Lời giải chi tiết :
Cơ năng con lắc sau 1 chu kì còn: \({{\rm{W}}_1} = (100\% - 5\% ).{{\rm{W}}_0} \Rightarrow {{\rm{W}}_n} = {(100\% - 5\% )^n}.{{\rm{W}}_0}\) Ta có: \(\begin{array}{l} Vậy sau 10 chu kỳ thì biên độ của con lắc còn : \({A_{10}} = \sqrt {{{\left( {95\% } \right)}^{10}}} .{A_0} = 77,4\% {A_0}\)
Câu 16 :
Một vật hình trụ tiết diện nhỏ, có chiều cao \(20\;{\rm{cm}}\), nổi thẳng đứng trong một bể nước rộng. Bỏ qua mọi lực cản, lấy \(g = 10\;{\rm{m}}/{{\rm{s}}^2}\). Khi cân bằng, một nửa vật bị chìm trong nước và mép dưới của vật cách đáy bể một đoạn đủ dài. Từ vị trí cân bằng của vật, truyền cho nó vận tốc ban đầu bằng \(1,5\;{\rm{m}}/{\rm{s}}\) hướng thẳng đứng xuống dưới. Kể từ lúc vật bắt đầu chuyển động đến lúc vận tốc của vật triệt tiêu lần đầu tiên thì tốc độ trung bình của vật gần nhất với giá trị nào sau đây?
Đáp án : C Phương pháp giải :
- Tìm các lực tác dụng vào vật khi cân bằng. - Khi tác dụng lực hướng xuống thì coi vật dao động điều hoà → tính lực kéo về → tính \(\omega \) và \(A.\) - Trong nước vật sẽ chuyển động chậm dần với gia tốc \(a \Rightarrow \)tính \(a.\) Lời giải chi tiết :
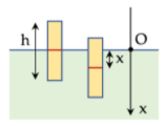
Khi vật cân bằng, tác dụng vào vật có trọng lực và lực đẩy Ác-si-mét: \(P = {F_A} \Rightarrow V{D_v}g = \frac{V}{2}{D_n}g \Rightarrow {D_n} = 2{D_v}\) Chọn trục \(Ox\) thẳng đứng hướng xuống: Khi vật chuyển động thì tác dụng vào vật có \({F_{kv}} = P - {F_A} \Leftrightarrow {F_{kv}} = mg - \frac{{{D_n}\left( {\frac{h}{2} + x} \right)}}{{{D_v}.h}}mg = \frac{{ - 2mg}}{h}x = - m{\omega ^2}x\) Tần số góc của dao động là: \(\omega = \sqrt {\frac{{2g}}{h}} = = \sqrt {\frac{{2.10}}{{0,2}}} = 10\left( {rad/s} \right)\) Biên độ dao động của vật là: \(A = \frac{{{v_{\max }}}}{\omega } = \frac{{150}}{{10}} = 15\left( {cm} \right)\) Nhận xét: \(A > \frac{h}{2} \to \) Vật đi xuống 1 đoạn bằng \({S_1} = \frac{h}{2} = 10\,cm\), khi này vật chìm hoàn toàn trong nước và có tốc độ là: \(v = \omega \sqrt {{A^2} - {x^2}} = 10\sqrt {{{15}^2} - {{10}^2}} = 0,5\sqrt 5 \left( {m/s} \right)\). Thời gian vật đi hết quãng đường \({S_1}\) là: \({t_1} = \frac{\alpha }{\omega } = \frac{{\arcsin \left( {\frac{{10}}{{15}}} \right)}}{{10}}\) Theo định luật II Niu – tơn: \(\begin{array}{l}{F_{kv}} = P - {F_A} \Rightarrow ma = mg - {D_n}.V.g\\ \Rightarrow {D_v}.V.a = {D_v}.V.g - {D_n}.V.g\end{array}\) Lúc này vật chuyển động chậm dần với gia tốc là \(a = \left( {1 - \frac{{{D_n}}}{{{D_v}}}} \right)g = - g = - 10\left( {m/{s^2}} \right)\) Do đó quãng đường và thời gian vật đi tiếp đến khi dừng là: \(\left\{ \begin{array}{l}S = \frac{{{v^2}}}{{2\left| a \right|}} = \frac{1}{{16}}m = 6,25\left( {cm} \right)\\{t_2} = \frac{v}{{\left| a \right|}} = \frac{1}{{4\sqrt 5 }}\left( s \right)\end{array} \right.\) Tốc độ trung bình của vật là: \({v_{tb}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}} = \frac{{10 + 6,25}}{{\frac{{ar\sin \left( {\frac{{10}}{{15}}} \right)}}{{10}} + \frac{1}{{4\sqrt 5 }}}} \approx 87,94\left( {cm/s} \right)\)
Câu 17 :
Đề thi THPT QG - 2020 Cho hệ vật gồm lò xo nhẹ có độ cứng k = 20 N/m, vật M có khối lượng 30 g được nối với vật N có khối lượng 150 g bằng một sợi dây không dãn vắt qua ròng rọc như hình bên. Bỏ qua mọi ma sát, bỏ qua khối lượng dây và ròng rọc. Ban đầu giữ M tại vị trí để lò xo không biến dạng, N ở xa mặt đất. Thả nhẹ M để cả hai vật cùng chuyển động, sau 0,2 s thì dây bị đứt. Sau khi dây đứt, M dao động điều hòa trên mặt phẳng nằm ngang với biên độ A. Lấy \(g = 10m/{s^2},{\mkern 1mu} {\mkern 1mu} ({\pi ^2} \approx 10).\) Giá trị của A bằng
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính độ dãn của lò xo tại vị trí CB khi treo thẳng đứng: \(\Delta l = \frac{{mg}}{k}\) + Sử dụng biểu thức tính tần số góc: \(\omega = \sqrt {\frac{k}{m}} \) + Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
Lúc đầu hệ hai vật dao động quanh vị trí cân bằng của chúng với biên độ \({A_{12}} = \Delta l\) với \(\Delta l = \frac{{{m_N}g}}{k} = \frac{{0,15.10}}{{20}} = 0,075 = 7,5cm\) Chu kỳ hệ 2 vật: \({T_{12}} = 2\sqrt {\frac{{{\pi ^2}\left( {{m_M} + {m_N}} \right)}}{k}} = 0,6s\) Sau 0,2 s kể từ khi hệ dao động \(t = 0,2s = \frac{{{T_{12}}}}{3} = \frac{{{T_{12}}}}{4} + \frac{{{T_{12}}}}{{12}}\) Cả hai vật đi được quãng đường: \({A_{12}} + \frac{{{A_{12}}}}{2}\) (Vật M là 1; vật N là 2) Lúc đó cà hai vật cùng vận tốc \(\left| {{v_{12}}} \right| = \frac{{\sqrt 3 }}{2}{v_{max}} = \frac{{25\sqrt {30} }}{2}cm/s\) Lúc sau vật 2 tách khỏi hệ chỉ còn vật 1 tham gia dao động. Vật 1 sẽ dao động quanh vị trí cân bằng của nó chính là vị trí lò xo không biến dạng với tần số góc mới \(\omega = \sqrt {\frac{k}{{{m_M}}}} = \frac{{20\sqrt {15} }}{3}\left( {rad/s} \right)\) Như vậy so với vị trí cân bằng của vật 1, vật 1 có tọa độ vận tốc: \(\left\{ \begin{array}{l}x = 7,5 + \frac{{7,5}}{2} = 11,25cm\\\left| v \right| = \frac{{25\sqrt {30} }}{2}cm/s\end{array} \right.\) Biên độ dao động mới \(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}} = 11,558cm\)
|



















Danh sách bình luận