Trắc nghiệm Bài 1. Ứng dụng vòng tròn lượng giác - Vật Lí 12Đề bài
Câu 1 :
Vận tốc của vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$ có độ lớn cực đại khi:
Câu 2 :
Gia tốc của một vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{{5\pi }}{6}} \right)$ có độ lớn cực đại. Khi:
Câu 3 :
Một vật dao động điều hòa với biên độ $A$ quanh vị trí cân bằng $0$, thời gian ngắn nhất để vật di chuyển từ vị trí có ly độ $x = - \dfrac{A}{2}$ đến vị trí có ly độ $x = A$ là $\dfrac{1}{2}s$, chu kỳ dao động:
Câu 4 :
Vật dao động điều hòa theo phương trình: \(x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\). Xác định thời gian ngắn nhất kể từ khi vật bắt đầu chuyển động đến vị trí có li độ \(x = \frac{{5\sqrt 2 }}{2}\) lần thứ nhất?
Câu 5 :
Một chất điểm dao động điều hòa với chu kì $T$ và biên độ $5cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ của chất điểm có độ lớn gia tốc không vượt quá $100cm/{s^2}$ là \(\dfrac{T}{3}\). Lấy ${\pi ^2} = 10$. Tần số dao động của vật là:
Câu 6 :
Một chất điểm đang dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều O. Biết cứ $0,05s$ thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó đi qua vị trí M, N là $20\pi \left( {cm/s} \right)$. Biên độ A bằng.
Câu 7 :
Một vật nhỏ dao động điều hòa với chu kì $T$ và biên độ $8 cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá $16 cm/s$ là $\dfrac{T}{3}$. Tần số góc của dao động là:
Câu 8 :
Một vật dao động điều hòa theo phương trình \(x = 8c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{6}} \right)cm\). Xác định thời gian vật chuyển động từ thời điểm $t=0,75s$ đến khi vật có li độ $x=-4 cm$ lần thứ $2$?
Câu 9 :
Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng $3 m/s$ và gia tốc cực đại bằng $30\pi m/{s^2}$. Thời điểm ban đầu $t = 0$ vật có vận tốc $v=+1,5 m/s$ và thế năng đang tăng. Hỏi sau đó bao lâu vật có gia tốc bằng $ - 15\pi m/{s^2}$
Câu 10 :
Một chất điểm dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {\dfrac{{2\pi }}{3}t} \right)cm\)(x tính bằng cm, t tính bằng giây). Kể từ $t=0$, chất điểm đi qua vị trí có li độ $x= -2cm$ lần thứ $2011$ tại thời điểm:
Câu 11 :
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
Câu 12 :
Một vật dao động điều hòa với phương trình: \(x = 8c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\). Thời điểm lần thứ $2010$ kể từ lúc bắt đầu dao động, vật qua vị trí có vận tốc $v= -8π cm/s$ là bao nhiêu?
Câu 13 :
Một vật dao động điều hòa với phương trình: \(x = 6c{\rm{os}}\left( {4\pi t + \frac{\pi }{4}} \right)cm\). Khoảng thời gian vật qua vị trí có li độ \(x = 3\sqrt 2 cm\) theo chiều dương lần thứ $2017$ kể từ lúc $t=0,125s$ là?
Câu 14 :
Một vật dao động theo phương trình \(x = 3\cos \left( {5\pi t - \frac{{2\pi }}{3}} \right)cm\). Trong giây đầu tiên vật qua vị trí cân bằng bao nhiêu lần?
Câu 15 :
Một chất điểm dao động điều hòa theo phương trình \(x = 3\sin \left( {5\pi t + \frac{\pi }{6}} \right)cm\) (x tính bằng cm, t tính bằng giây). Trong một giây đầu tiên từ thời điểm $t = 0,4s$, chất điểm đi qua vị trí có li độ $x = + 1 cm$
Câu 16 :
Một vật dao động điều hoà với phương trình \(x = 8\cos \left( {2\pi t - \frac{\pi }{3}} \right)cm\). Tìm số lần vật qua vị trí có vận tốc \(v = - 8\pi \left( {cm/s} \right)\) trong thời gian $5,75s$ tính từ thời điểm gốc.
Câu 17 :
Một vật dao động điều hoà với phương trình $x = 4c{\rm{os}}\left( {4\pi t + \dfrac{\pi }{6}} \right)cm$. Tìm số lần vật qua vị trí có gia tốc là $32{\pi ^2}cm/{s^2}$ theo chiều dương trong thời gian $5,75s$ tính từ thời điểm gốc.
Câu 18 :
Hai điểm sáng cùng dao động trên trục Ox với các phương trình li độ lần lượt là \({x_1} = Acos\left( {2\pi t + \dfrac{\pi }{6}} \right)\) ; \({x_2} = Acos\left( {2\pi t + \dfrac{{5\pi }}{6}} \right)\). Thời điểm mà hai điểm sáng có cùng li độ lần thứ 2020 là
Lời giải và đáp án
Câu 1 :
Vận tốc của vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{\pi }{3}} \right)$ có độ lớn cực đại khi:
Đáp án : D Phương pháp giải :
+ Vận tốc của vật có độ lớn cực đại khi vật ở VTCB + Xác định li độ và chiều của vận tốc tại thời điểm ban đầu $t = 0$ + Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn Lời giải chi tiết :
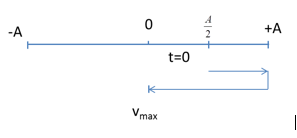 Ta có, vận tốc của vật có độ lớn cực đại khi vật ở VTCB Tại thời điểm ban đầu t =0 : \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{\pi }{3}} \right) = \dfrac{A}{2}\\v = - A\omega \sin \left( { - \dfrac{\pi }{3}} \right) > 0\end{array} \right.\) => Vận tốc của vật có độ lớn cực đại khi \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}}\)
Câu 2 :
Gia tốc của một vật dao động điều hoà có phương trình li độ $x = A\cos \left( {\omega t - \dfrac{{5\pi }}{6}} \right)$ có độ lớn cực đại. Khi:
Đáp án : A Phương pháp giải :
+ Gia tốc của vật có độ lớn cực đại khi vật ở biên + Xác định li độ và chiều của vận tốc tại thời điểm ban đầu $t = 0$ + Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn Lời giải chi tiết :
Ta có, Gia tốc của vật có độ lớn cực đại khi vật ở biên Tại thời điểm ban đầu t =0 : \(\left\{ \begin{array}{l}x = Ac{\rm{os}}\left( { - \dfrac{{5\pi }}{6}} \right) = - \dfrac{{A\sqrt 3 }}{2}\\v = - A\omega \sin \left( { - \dfrac{{5\pi }}{6}} \right) > 0\end{array} \right.\) => Gia tốc của vật có độ lớn cực đại khi \(t = \dfrac{T}{6} + \dfrac{T}{4} = \dfrac{{5T}}{{12}}\)
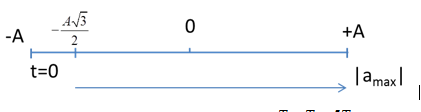
Câu 3 :
Một vật dao động điều hòa với biên độ $A$ quanh vị trí cân bằng $0$, thời gian ngắn nhất để vật di chuyển từ vị trí có ly độ $x = - \dfrac{A}{2}$ đến vị trí có ly độ $x = A$ là $\dfrac{1}{2}s$, chu kỳ dao động:
Đáp án : A Phương pháp giải :
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn Lời giải chi tiết :
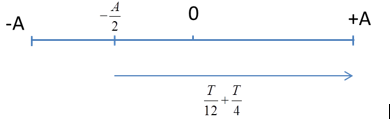 Ta có, thời gian ngắn nhất để vật di chuyển từ $x = - \dfrac{A}{2}$ đến A là : \(t = \dfrac{T}{{12}} + \dfrac{T}{4} = \dfrac{T}{3} = \dfrac{1}{2}s \to T = 1,5{\rm{s}}\)
Câu 4 :
Vật dao động điều hòa theo phương trình: \(x = 5c{\rm{os}}\left( {2\pi t - \frac{\pi }{3}} \right)cm\). Xác định thời gian ngắn nhất kể từ khi vật bắt đầu chuyển động đến vị trí có li độ \(x = \frac{{5\sqrt 2 }}{2}\) lần thứ nhất?
Đáp án : C Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ: $T = \frac{{2\pi }}{\omega }$
+ Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn Lời giải chi tiết :
Ta có: Chu kỳ dao động của vật: $T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}$ Tại thời điểm ban đầu t=0: $\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( { - \frac{\pi }{3}} \right) = 2,5cm\\v = - 10\pi \sin \left( { - \frac{\pi }{3}} \right) = 5\sqrt 3 \pi > 0\end{array} \right.$
$ \to t = \frac{T}{{24}} = \frac{1}{{24}}s$ 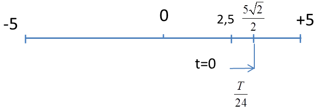
Câu 5 :
Một chất điểm dao động điều hòa với chu kì $T$ và biên độ $5cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ của chất điểm có độ lớn gia tốc không vượt quá $100cm/{s^2}$ là \(\dfrac{T}{3}\). Lấy ${\pi ^2} = 10$. Tần số dao động của vật là:
Đáp án : D Phương pháp giải :
Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn hoặc sử dụng công thức $\Delta t = \dfrac{{\Delta \varphi }}{\omega }$ để suy ra vị trí của điểm a theo amax Lời giải chi tiết :
Khoảng thời gian gia tốc biến thiên từ 0 đến vị trí gia tốc có độ lớn 100cm/s2 là: $\Delta t = \dfrac{{\dfrac{T}{3}}}{4} = \dfrac{T}{{12}}$ => Vị trí $\left| a \right| = 100cm/{s^2} = \dfrac{{{a_{{\rm{max}}}}}}{2} \to {a_{{\rm{max}}}} = 2{\rm{a}}$ \(\begin{array}{l} \to {\omega ^2}A = 2.a \to \omega = \sqrt {\dfrac{{2{\rm{a}}}}{A}} = \sqrt {\dfrac{{2.100}}{5}} = 2\pi \\ \to f = \dfrac{\omega }{{2\pi }} = 1H{\rm{z}}\end{array}\) 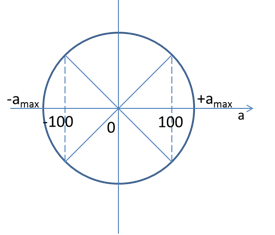
Câu 6 :
Một chất điểm đang dao động điều hòa trên một đoạn thẳng xung quanh vị trí cân bằng O. Gọi M, N là hai điểm trên đường thẳng cùng cách đều O. Biết cứ $0,05s$ thì chất điểm lại đi qua các điểm M, O, N và tốc độ của nó đi qua vị trí M, N là $20\pi \left( {cm/s} \right)$. Biên độ A bằng.
Đáp án : A Phương pháp giải :
+ Xác định vị trí M, N trên vòng tròn lượng giác + Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn + Sử dụng công thức xác định chu kỳ: \(T = \dfrac{{2\pi }}{\omega }\) + Sử dụng hệ thức độc lập xác định biên độ A: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
Ta có: M, N cách đều O và cứ $0,05s$ thì chất điểm lại đi qua các điểm M, O, N => các điểm D, B, G, E cách đều nhau 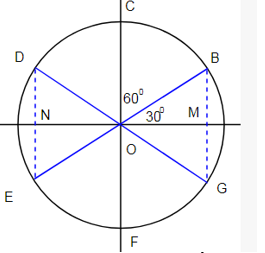 Từ vòng tròn lượng giác: \( \to {x_M} = {x_N} = \dfrac{{A\sqrt 3 }}{2}\) \( \to \dfrac{T}{6} = 0,05s \to T = 0,3{\rm{s}} \to \omega = \dfrac{{2\pi }}{T} = \dfrac{{20\pi }}{3}ra{\rm{d}}/s\) Sử dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = \dfrac{{3{A^2}}}{4} + {\left( {\dfrac{{20\pi }}{{\dfrac{{20\pi }}{3}}}} \right)^2} \to \dfrac{{{A^2}}}{4} = 9 \to A = 6cm\)
Câu 7 :
Một vật nhỏ dao động điều hòa với chu kì $T$ và biên độ $8 cm$. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn vận tốc không vượt quá $16 cm/s$ là $\dfrac{T}{3}$. Tần số góc của dao động là:
Đáp án : C Phương pháp giải :
+ Sử dụng vòng tròn lượng giác và thời gian trên đường thẳng được suy ra từ đường tròn + Sử dụng công thức tính vận tốc cực đại: vmax = Aω Lời giải chi tiết :
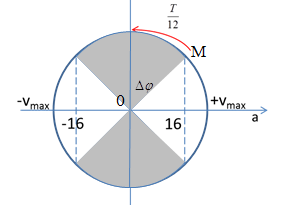 Khoảng thời gian \(\dfrac{T}{3}\) ứng với vùng màu xám trong hình trên Ta suy ra: Khoảng thời gian vận tốc biến thiên từ 0 đến vị trí vận tốc có độ lớn \(16cm/{s^2}\) là: \(\Delta t = \dfrac{{\dfrac{T}{3}}}{4} = \dfrac{T}{{12}}\) Cách 1: => Vị trí \(\left| v \right| = 16cm/s = \dfrac{{{v_{{\rm{max}}}}}}{2} \to {v_{{\rm{max}}}} = 2v \leftrightarrow A\omega = 2v \to \omega = \dfrac{{2v}}{A} = \frac{{2.16}}{8} = 4{\rm{r}}a{\rm{d}}/s\) Cách 2: Từ vòng tròn lượng giác, ta có góc quét \(\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{{12}} = \dfrac{\pi }{6}rad\) \(\begin{array}{l}OM.\sin \Delta \varphi = 16\\ \leftrightarrow A\omega .\sin \Delta \varphi = 16\\ \to \omega = \dfrac{{16}}{{A.\sin \Delta \varphi }} = \dfrac{{16}}{{8.\sin \dfrac{\pi }{6}}} = 4\left( {rad/s} \right)\end{array}\)
Câu 8 :
Một vật dao động điều hòa theo phương trình \(x = 8c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{6}} \right)cm\). Xác định thời gian vật chuyển động từ thời điểm $t=0,75s$ đến khi vật có li độ $x=-4 cm$ lần thứ $2$?
Đáp án : A Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm t (x,v) + Sử dụng trục thời gian trên đường thẳng được suy ra từ đường tròn Lời giải chi tiết :
Ta có: Chu kỳ: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1s\) Tại thời điểm t=0,75s: \(\left\{ \begin{array}{l}x = 8c{\rm{os}}\left( {2\pi .0,75 + \dfrac{\pi }{6}} \right) = 4cm\\v = - 16\pi \sin \left( {2\pi .0,75 + \dfrac{\pi }{6}} \right) = 8\sqrt 3 \pi > 0\end{array} \right.\) 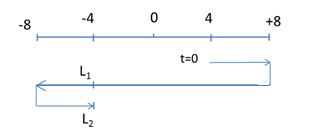 => Khoảng thời gian: \(\Delta t = \dfrac{T}{6} + \dfrac{T}{2} + \dfrac{T}{6} = \dfrac{{5T}}{6} = \dfrac{5}{6}s\)
Câu 9 :
Một vật dao động được kích thích để dao động điều hòa với vận tốc cực đại bằng $3 m/s$ và gia tốc cực đại bằng $30\pi m/{s^2}$. Thời điểm ban đầu $t = 0$ vật có vận tốc $v=+1,5 m/s$ và thế năng đang tăng. Hỏi sau đó bao lâu vật có gia tốc bằng $ - 15\pi m/{s^2}$
Đáp án : A Phương pháp giải :
+Sử dụng công thức \(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right.\) tính chu kì và biên độ dao động của vật. + Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) + Xác định vị trí tại thời điểm t=0 (x,v) + Sử dụng công thức \(a = - {\omega ^2}x\) + Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\) Lời giải chi tiết :
Ta có: \(\left\{ \begin{array}{l}{v_{{\rm{max}}}} = \omega A\\{a_{{\rm{max}}}} = {\omega ^2}A\end{array} \right. \to \left\{ \begin{array}{l}\frac{{{a_{{\rm{max}}}}}}{{{v_{{\rm{max}}}}}} = \omega = \frac{{30\pi }}{3} = 10\pi \\A = \frac{{{v_{{\rm{max}}}}}}{\omega } = \frac{3}{{10\pi }}m\end{array} \right.\) Tại t = 0: v = +1,5m/s và thế năng đang tăng Sử dụng hệ thức độc lập, ta có: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \to {x^2} = {A^2} - \frac{{{v^2}}}{{{\omega ^2}}} = {\left( {\frac{3}{{10\pi }}} \right)^2} - \frac{{1,{5^2}}}{{{{\left( {10\pi } \right)}^2}}} \to x = \frac{{1,5\sqrt 3 }}{{10\pi }} = \frac{{A\sqrt 3 }}{2}\) Khi vật có gia tốc \(a = - 15\pi \left( {m/{s^2}} \right) = - {\omega ^2}{x_2} \to {x_2} = - \frac{{ - 15\pi }}{{{{\left( {10\pi } \right)}^2}}} = \frac{{1,5}}{{10\pi }} = \frac{A}{2}\) => Thời gian để vật đi từ t =0 đến vị trí có a = 15π (m/s2) là: \(t = \frac{T}{{12}} + \frac{T}{6} = \frac{T}{4} = \frac{1}{4}\frac{{2\pi }}{\omega } = 0,05s\) 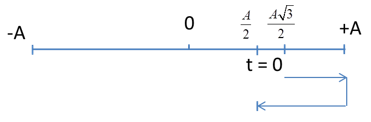
Câu 10 :
Một chất điểm dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {\dfrac{{2\pi }}{3}t} \right)cm\)(x tính bằng cm, t tính bằng giây). Kể từ $t=0$, chất điểm đi qua vị trí có li độ $x= -2cm$ lần thứ $2011$ tại thời điểm:
Đáp án : C Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \dfrac{{2\pi }}{\omega }\) + Sử dụng công thức xác định thời điểm vật đi qua li độ x lần thứ n (với n lẻ) : \(t = \dfrac{{n - 1}}{2}T + {t_1}\) + Xác định vị trí tại thời điểm $t=0 (x,v)$ Lời giải chi tiết :
Ta có: Chu kỳ: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{\dfrac{{2\pi }}{3}}} = 3s\) Trong một chu kỳ, chất điểm đi qua vị trí có li độ $x=-2cm$ hai lần => \({t_{2011}} = \frac{{2011 - 1}}{2}T + {t_1} = 1005T + {t_1}\) Tại $t=0$, vật ở li độ: $x=4cm$ => t1 là khoảng thời gian chất điểm đi từ $A$ (vị trí ban đầu) đến $-A/2$ => \({t_1} = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{T}{3}\) \( \to {t_{2011}} = 1005T + {t_1} = 1005T + \dfrac{T}{3} = \dfrac{{3016T}}{3} = \dfrac{{3016.3}}{3} = 3016{\rm{s}}\)
Câu 11 :
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
Đáp án : B Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ $T$: \(T = \dfrac{{2\pi }}{\omega }\) + Sử dụng công thức xác định thời điểm vật đi qua li độ x lần thứ $n$ (với $n$ chẵn) : \(t = \dfrac{{n - 2}}{2}T + {t_2}\) + Xác định vị trí tại thời điểm $t=0 (x,v)$ Lời giải chi tiết :
Ta có: Chu kỳ: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = 0,1s\) \(\left\{ \begin{gathered} Bài toán đưa về dạng xác định thời điểm vật qua li độ $x=0$ lần thứ $n$ ($n$ chẵn) => \({t_{2016}} = \frac{{2016 - 2}}{2}T + {t_2} = 1007T + {t_2}\) Tại $t=0$: \(\left\{ \begin{array}{l}x = 10c{\rm{os}}\left( {\dfrac{{ - \pi }}{6}} \right) = 5\sqrt 3 cm\\v = - 10.20\pi sin\left( {\dfrac{{ - \pi }}{6}} \right) = 100\pi > 0\end{array} \right.\) $t_2$ là khoảng thời gian từ lúc bắt đầu đến khi qua $x=0$ lần thứ $2$ => \({t_2} = \dfrac{T}{{12}} + \dfrac{{3T}}{4} = \dfrac{{5T}}{6}\) \( \to {t_{2016}} = 1007T + {t_2} = 1007T + \dfrac{{5T}}{6} = \dfrac{{6047T}}{6} = \dfrac{{6047.0,1}}{6} = 100,783{\rm{s}}\) 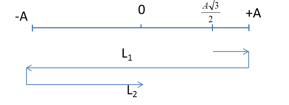
Câu 12 :
Một vật dao động điều hòa với phương trình: \(x = 8c{\rm{os}}\left( {2\pi t - \dfrac{\pi }{6}} \right)cm\). Thời điểm lần thứ $2010$ kể từ lúc bắt đầu dao động, vật qua vị trí có vận tốc $v= -8π cm/s$ là bao nhiêu?
Đáp án : A Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \dfrac{{2\pi }}{\omega }\) + Sử dụng công thức xác định thời điểm vật đi qua li độ x lần thứ n (với n chẵn) : \(t = \dfrac{{n - 2}}{2}T + {t_2}\) + Xác định vị trí tại thời điểm t=0 (x,v) + Sử dụng hệ thức độc lập A-x-v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
Ta có: Chu kỳ dao động: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\) Tại $t=0$: \(\left\{ \begin{array}{l}x = 8c{\rm{os}}\left( { - \dfrac{\pi }{6}} \right) = 4\sqrt 3 cm\\v = - 16\pi \sin \left( { - \dfrac{\pi }{6}} \right) = 8\pi > 0\end{array} \right.\) Tại vị trí có $v= -8π cm/s$: \(x = \pm \sqrt {{A^2} - \dfrac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {{8^2} - \dfrac{{{{\left( {8\pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = \pm 4\sqrt 3 cm\) Trong một chu kỳ, vật đi qua vị trí có vận tốc $v= -8πcm/s$ 2 lần \( \to {t_{2010}} = \dfrac{{2010 - 2}}{2}T + {t_2} = 1004T + {t_2}\) t2 là khoảng thời gian từ lúc bắt đầu đến khi vật đạt vận tốc $v= -8πcm/s$ lần thứ 2. 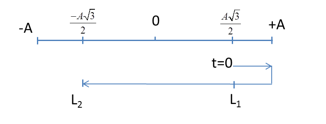 \( \to {t_2} = \dfrac{T}{{12}} + \dfrac{T}{4} + \dfrac{T}{6} = \dfrac{T}{2}\) \( \to {t_{2010}} = 1004T + {t_2} = 1004T + \dfrac{T}{2} = 1004,5T = 1004,5{\rm{s}}\)
Câu 13 :
Một vật dao động điều hòa với phương trình: \(x = 6c{\rm{os}}\left( {4\pi t + \frac{\pi }{4}} \right)cm\). Khoảng thời gian vật qua vị trí có li độ \(x = 3\sqrt 2 cm\) theo chiều dương lần thứ $2017$ kể từ lúc $t=0,125s$ là?
Đáp án : D Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\) + Sử dụng công thức xác định khoảng thời gian vật qua vị trí x khi kể đến chiều: \(t = (n - 1)T + {t_1}\) + Xác định vị trí tại thời điểm t (x,v) Lời giải chi tiết :
Ta có: Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) Tại $t=0,125s$: \(\left\{ \begin{array}{l}x = 6c{\rm{os}}\left( {4\pi .0,125 + \frac{\pi }{4}} \right) = - 3\sqrt 2 cm\\v = - 24\pi \sin \left( {4\pi .0,125 + \frac{\pi }{4}} \right) = - 12\sqrt 2 \pi < 0\end{array} \right.\) Trong một chu kỳ, vật đi qua vị trí \(x = 3\sqrt 2 cm\)theo chiều dương 1 lần. \( \to {t_{2017}} = 2016T + {t_1}\) \(x = 3\sqrt 2 cm\)theo chiều dương lần thứ 1 \( \to {t_1} = \frac{T}{8} + \frac{T}{4} + \frac{T}{8} = \frac{T}{2}\) \( \to {t_{2017}} = 2016T + {t_1} = 2016T + \frac{T}{2} = 2016,5T = 1008,25{\rm{s}}\) 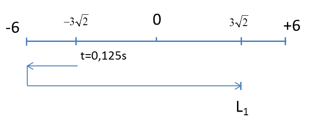
Câu 14 :
Một vật dao động theo phương trình \(x = 3\cos \left( {5\pi t - \frac{{2\pi }}{3}} \right)cm\). Trong giây đầu tiên vật qua vị trí cân bằng bao nhiêu lần?
Đáp án : C Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \dfrac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm $t=0 (x,v)$ Lời giải chi tiết :
Ta có: Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{5\pi }} = 0,4{\rm{s}}\) Tại $t=0s$: \(\left\{ \begin{array}{l}x = 3c{\rm{os}}\left( { - \frac{{2\pi }}{3}} \right) = - 1,5cm\\v = - A\omega \sin \left( { - \frac{{2\pi }}{3}} \right) > 0\end{array} \right.\) ta có: \(1{\rm{s}} = 2T + \frac{T}{2}\) Trong một chu kỳ, vật đi qua vị trí VTCB $2$ lần Trong khoảng thời gian $T/2$ vật qua vị trí cân bằng $1$ lần kể từ $t = 0$ => Trong $1s$ đầu tiên, vật qua VTCB số lần là: $2.2 + 1 = 5$ lần
Câu 15 :
Một chất điểm dao động điều hòa theo phương trình \(x = 3\sin \left( {5\pi t + \frac{\pi }{6}} \right)cm\) (x tính bằng cm, t tính bằng giây). Trong một giây đầu tiên từ thời điểm $t = 0,4s$, chất điểm đi qua vị trí có li độ $x = + 1 cm$
Đáp án : C Phương pháp giải :
+ Viết phương trình dao động về dạng $x = Acos(ωt + φ)$ + Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm $t=0,4s (x,v)$ Lời giải chi tiết :
\(x = 3sin(5\pi t + \frac{\pi }{6}) = 3c{\rm{os}}\left( {5\pi t + \frac{\pi }{6} - \frac{\pi }{2}} \right) = 3c{\rm{os}}\left( {5\pi t - \frac{\pi }{3}} \right)cm\) Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{5\pi }} = 0,4{\rm{s}}\) Tại t=0,4s: \(\left\{ \begin{array}{l}x = 3c{\rm{os}}\left( { - \frac{\pi }{3}} \right) = 1,5cm\\v = - A\omega \sin \left( { - \frac{\pi }{3}} \right) > 0\end{array} \right.\) ta có: \(1{\rm{s}} = 2T + \frac{T}{2}\) Trong một chu kỳ, vật đi qua vị trí $+1cm$ $2$ lần Trong khoảng thời gian $T/2$ vật qua vị trí $+1cm$ $1$ lần kể từ $t = 0,4s$ => Trong 1s đầu tiên kể từ $t = 0,4s$, vật qua vị trí $+1cm$ số lần là: $2.2 + 1 = 5$ lần
Câu 16 :
Một vật dao động điều hoà với phương trình \(x = 8\cos \left( {2\pi t - \frac{\pi }{3}} \right)cm\). Tìm số lần vật qua vị trí có vận tốc \(v = - 8\pi \left( {cm/s} \right)\) trong thời gian $5,75s$ tính từ thời điểm gốc.
Đáp án : C Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm $t=0 (x,v)$ + Sử dụng hệ thức độc lập \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\) Lời giải chi tiết :
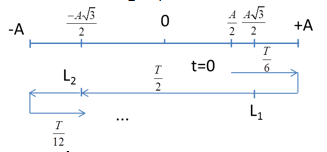 Ta có: Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1{\rm{s}}\) Tại t=0s: \(\left\{ \begin{array}{l}x = 8c{\rm{os}}\left( { - \frac{\pi }{3}} \right) = 4cm\\v = - A\omega \sin \left( { - \frac{{\pi }}{3}} \right) > 0\end{array} \right.\) Tại vị trí có v= -8π cm/s: \(x = \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {{8^2} - \frac{{{{\left( {8\pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}} = \pm 4\sqrt 3 cm\) Trong một chu kỳ, vật đi qua vị trí có vận tốc v= -8πcm/s 2 lần Ta có: \({\rm{5,75s}} = 5T + \frac{T}{2} + \frac{T}{4}\) Trong khoảng thời gian T/4 + T/2 vật qua vị trí có vận tốc v= -8πcm/s 2 lần lần kể từ t = 0 => Trong 5,75s đầu tiên, vật qua vị trí có vận tốc v= -8πcm/s số lần là: 2.5 + 2 = 12 lần
Câu 17 :
Một vật dao động điều hoà với phương trình $x = 4c{\rm{os}}\left( {4\pi t + \dfrac{\pi }{6}} \right)cm$. Tìm số lần vật qua vị trí có gia tốc là $32{\pi ^2}cm/{s^2}$ theo chiều dương trong thời gian $5,75s$ tính từ thời điểm gốc.
Đáp án : D Phương pháp giải :
+ Sử dụng công thức xác định chu kỳ T: \(T = \frac{{2\pi }}{\omega }\) + Xác định vị trí tại thời điểm $t=0 (x,v)$ Lời giải chi tiết :
Ta có: Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\) Tại $t=0s$: \(\left\{ \begin{array}{l}x = 4c{\rm{os}}\left( {\frac{\pi }{6}} \right) = 2\sqrt 3 cm\\v = - A\omega \sin \left( {\frac{\pi }{6}} \right) < 0\end{array} \right.\) Tại vị trí có: \(a = {32{\pi ^2}}cm/{s^2} = - {\omega ^2}{x_2} \to {x_2} = - \frac{{32{\pi ^2}}}{{{{(4\pi )}^2}}} = - 2cm\) Trong một chu kỳ, vật đi qua vị trí $-2cm$ theo chiều dương $1$ lần Ta có: \({\rm{5,75s}} = 11T + \frac{T}{2}\) Trong khoảng thời gian $T/2$ vật qua vị trí $-2cm$ theo chiều dương $0$ lần kể từ $t = 0$ => Trong $5,75s$ đầu tiên, vật qua vị trí $-2cm$ số lần là: $11 + 0 = 11$ lần
Câu 18 :
Hai điểm sáng cùng dao động trên trục Ox với các phương trình li độ lần lượt là \({x_1} = Acos\left( {2\pi t + \dfrac{\pi }{6}} \right)\) ; \({x_2} = Acos\left( {2\pi t + \dfrac{{5\pi }}{6}} \right)\). Thời điểm mà hai điểm sáng có cùng li độ lần thứ 2020 là
Đáp án : C Phương pháp giải :
Vận dụng vòng tròn lượng giác và trục thời gian suy ra từ vòng tròn Lời giải chi tiết :
Chu kì dao động của 2 điểm sáng \(T = 1s\) Ta có li độ của 2 điểm sáng bằng nhau: \({x_1} = {x_2}\) \(\Rightarrow d = {x_1} - {x _2} = 0\) Ta có: \({x_1} - {x_2} = A\angle \dfrac{\pi }{6} - A\angle \dfrac{{5\pi }}{6} = A\sqrt 3 \angle 0\) \( \Rightarrow d = A\sqrt 3 cos\left( {2\pi t} \right)\) Trong 1 chu kì có 2 vị trí \(d = 0\) \({t_{2020}} = {t_{2018}} + {t_2}\) \({t_{2018}} = \dfrac{{2018T}}{2} = 1009T\)
Từ vòng tròn lượng giác ta suy ra \({t_2} = \dfrac{{3T}}{4}\) \( \Rightarrow {t_{2020}} = 1009T + \dfrac{{3T}}{4} = \dfrac{{4039T}}{4} = \dfrac{{4039.1}}{4} = 1009,75s\)
|




















Danh sách bình luận