Trắc nghiệm Tổng hợp bài tập các loại dao động - Vật Lí 12Đề bài
Câu 1 :
Dao động tắt dần là dao động có:
Câu 2 :
Phát biểu nào sau đây là đúng khi nói về dao động tắt dần?
Câu 3 :
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là
Câu 4 :
Nhận định nào sau đây sai khi nói về dao động cơ học tắt dần?
Câu 5 :
Một vật dao động cưỡng bức dưới tác dụng của một ngoại lực biến thiên điều hòa với tần số $f$. Chu kì dao động của vật là:
Câu 6 :
Khi nói về một hệ dao động cưỡng bức ở giai đoạn ổn định, phát biểu nào dưới đây là sai?
Câu 7 :
Khi nói về dao động cưỡng bức, phát biểu nào sau đây là đúng?
Câu 8 :
Khi nói về một hệ dao động cưỡng bức ở giai đoạn ổn định, phát biểu nào dưới đây là sai?
Câu 9 :
Con lắc lò xo gồm vật nặng m = 100g và lò xo nhẹ có độ cứng \(k = 100N/m\). Tác dụng một ngoại lực cưỡng bức biến thiên điều hòa biên độ \(F_0\) và tần số \(f_1 = 6Hz\) thì biên độ dao động là \(A_1\). Nếu giữ nguyên biên độ \(F_0\) mà tăng tần số ngoại lực đến \(f_2=5,5Hz\) thì biên độ dao động ổn định là \(A_2\). Kết luận đúng là:
Câu 10 :
Chọn phát biểu đúng: Dao động duy trì của một hệ là dao động tắt dần mà người ta đã:
Câu 11 :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động:
Câu 12 :
Dao động tự do là hệ dao động xảy ra dưới tác dụng của:
Câu 13 :
Tần số của hệ dao động tự do:
Câu 14 :
Phát biểu nào sau đây là sai khi nói về dao động cơ học
Câu 15 :
Khi xảy ra hiện tượng cộng hưởng thì:
Câu 16 :
Một người xách một xô nước đi trên đường, mỗi bước dài 45cm. Chu kì dao động riêng của nước trong xô là 0,3s. Để nước trong xô bị dao động mạnh nhất người đó phải đi với tốc độ
Câu 17 :
Một tấm ván bắc qua một con mương có tần số dao động riêng là 0,5Hz. Một người đi qua tấm ván với bao nhiêu bước trong 12 giây thì tấm ván bị rung lên mạnh nhất?
Câu 18 :
Một vật có khối lượng 100g gắn với một lò xo có độ cứng 100N/m. Vật chỉ dao động được trên trục Ox nằm ngang trùng với trục của lò xo. Ban đầu, kéo vật ra khỏi vị trí cân bằng 8cm, rồi truyền cho vật vận tốc 60cm/s hướng theo phương Ox. Trong quá trình dao động vật luôn chịu tác dụng một lực cản không đổi 0,02N. Tổng chiều dài quãng đường mà vật đi được từ lúc bắt đầu dao động cho tới lúc dừng lại:
Câu 19 :
Một con lắc lò xo có độ cứng 62,5 N/m, vật nặng có khối lượng m=100g dao động trên mặt phẳng nằm ngang. Hệ số masát giữa vật và mặt phẳng ngang là μ=0,1; lấy g=10m/s2. Kéo vật khỏi vị trí cân bằng một đoạn A rồi thả nhẹ. Quãng đường mà vật đã đi cho đến khi dừng hẳn là 2,4m. Giá trị của A là:
Câu 20 :
Một con lắc lò xo đang dao động tắt dần, sau ba chu kì đầu tiên biên độ của nó giảm đi 10%. Phần trăm cơ năng còn lại sau khoảng thời gian đó là:
Câu 21 :
Một con lắc dao động tắt dần trong môi trường với lực masát rất nhỏ. Cứ sau mỗi chu kì, phần năng lượng của con lăc bị mất đi 8%. Trong một dao động toàn phần biên độ giảm đi bao nhiêu phần trăm?
Câu 22 :
Con lắc lò xo dao động theo phương ngang, lò xo nhẹ có độ cứng 100N/m, vật nhỏ dao động có khối lượng 100g, hệ số ma sát giữa vật và mặt phẳng ngang là 0,01. Tính độ giảm biên độ mỗi lần vật qua vị trí cân bằng.
Câu 23 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là 5J. Sau ba chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi 18%. Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Câu 24 :
Một con lắc lò xo, vật nặng có khối lượng 100g, lò xo có độ cứng 100N/m, dao động trên mặt phẳng ngang với biên độ ban đầu 10cm. Lấy gia tốc trọng trường 10m/s2. Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,1. Số dao động thực hiện được kể từ lúc dao động cho đến lúc dừng lại là:
Câu 25 :
Một con lắc lò xo, vật nặng có khối lượng 100g, lò xo có độ cứng 100N/m, dao động trên mặt phẳng ngang với biên độ ban đầu 10cm. Lấy gia tốc trọng trường 10m/s2. Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,1. Tìm thời gian từ lúc dao động cho đến lúc dừng lại.
Câu 26 :
Một vật nhỏ nối với một lò xo nhẹ, hệ dao động trên mặt phẳng ngang. Từ vị trí cân bằng truyền cho vật vận tốc ban đầu 2m/s theo phương ngang thì vật dao động tắt dần. Tốc độ trung bình trong suốt quá trình vật dao động là:
Câu 27 :
Thực hiện thí nghiệm về dao động cưỡng bức như hình bên. Năm con lắc đơn: (1), (2), (3), (4) và M (con lắc điều khiển) được treo trên một sợi dây. Ban đầu hệ đang đứng yên ở vị trí cân bằng. Kích thích M dao động nhỏ trong mặt phẳng vuông góc với mặt phẳng hình vẽ thì các con lắc còn lại dao động theo. Không kể M, con lắc dao động mạnh nhất là 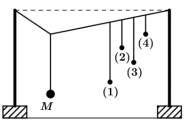
Câu 28 :
Giảm xóc của ô tô là áp dụng của
Câu 29 :
Một con lắc lò xo dao động tắt dần trên mặt phẳng nằm ngang. Cứ sau mỗi chu kì biên độ giảm 2%. Gốc thế năng tại vị trí của vật mà lò xo không biến dạng. Phần trăm cơ năng của con lắc bị mất đi trong hai dao động toàn phần liên tiếp có giá trị gần nhất với giá trị nào sau đây?
Câu 30 :
Con lắc đơn dao động trong môi trường không khí. Kéo con lắc lệch phương thẳng đứng một góc 0,1 rad rồi thả nhẹ. Biết lực cản của không khí tác dụng lên con lắc là không đổi và bằng 0,001 lần trọng lượng của vật. Coi biên độ giảm đều trong từng chu kỳ. Số lần con lắc qua vị trí cân bằng đến lúc dừng lại là:
Câu 31 :
Một vật chịu tác dụng của ngoại lực có biểu thức Fn = F0cos(10πt + π/2) thì xảy ra hiện tượng cộng hưởng. Tần số dao động riêng của vật là
Câu 32 :
Một con lắc lò xo gồm vật nhỏ nhỏ có khối lượng 100 gam và lò xo nhẹ có độ cứng 40 N/m. Cho con lắc dao động lần lượt dưới tác dụng của ngoại lực: F1 = 2cos5t (N); F2 = 2cos20t (N); F3 = 2cos30t (N) và F4 = 2cos25t (N), trong đó t tính bằng s. Hiện tượng cộng hưởng xảy ra khi con lắc chịu tác dụng của ngoại lực là
Câu 33 :
Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động
Câu 34 :
Đề thi THPT QG - 2020 Một con lắc đơn có chiều dài 70 cm đang dao động cưỡng bức với biên độ góc nhỏ, tại nơi có g=10m/s2. Khi có cộng hưởng, con lắc dao động điều hòa với chu kì là
Câu 35 :
Hai chất điểm dao động có li độ phụ thuộc theo thời gian được biểu diễn tương ứng bởi hai đồ thị (1) và (2) như hình vẽ, Nhận xét nào dưới đây đúng khi nói về dao động của hai chất điểm?
Câu 36 :
Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng \(216g\) và lò xo có độ cứng \(k\), dao động dưới tác dụng của ngoại lực \(\text{F = }{{\text{F}}_{\text{0}}}\text{cos2 }\!\!\pi\!\!\text{ ft}\), với \({{F}_{0}}\) không đổi và \(f\) thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ \(A\) của con lắc theo tần số \(f\) có đồ thị như hình vẽ. Giá trị của \(k\) gần nhất với giá trị nào sau đây?
Câu 37 :
Một cây cầu bắc ngang qua sông Phô-tan-ka ở thành phố Xanh Pê-téc-bua (Nga) được thiết kế xây dựng đủ vững chắc, có thể cho cùng lúc 300 người đi qua mà cầu không sập. Năm 1906 có một trung đội bộ binh gồm 36 người đi đều bước qua cây cầu làm cho cây cầu gãy. Sự cố gãy cầu là do
Lời giải và đáp án
Câu 1 :
Dao động tắt dần là dao động có:
Đáp án : C Lời giải chi tiết :
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Câu 2 :
Phát biểu nào sau đây là đúng khi nói về dao động tắt dần?
Đáp án : A Lời giải chi tiết :
Ta có: Dao động tắt dần là dao động có biên độ giảm dần theo thời gian Mặt khác: Cơ năng tỉ lệ thuận với bình phương biên độ: \({\text{W}} = \frac{1}{2}k{A^2}\) => Cơ năng của dao động tắt dần giảm dần theo thời gian
Câu 3 :
Một vật dao động tắt dần có các đại lượng giảm liên tục theo thời gian là
Đáp án : C Lời giải chi tiết :
Ta có: Dao động tắt dần là dao động có biên độ giảm dần theo thời gian Mặt khác: Cơ năng (năng lượng) tỉ lệ thuận với bình phương biên độ: \({\text{W}} = \frac{1}{2}k{A^2}\) => Cơ năng (năng lượng) của dao động tắt dần cũng giảm dần theo thời gian
Câu 4 :
Nhận định nào sau đây sai khi nói về dao động cơ học tắt dần?
Đáp án : A Lời giải chi tiết :
B, C, D - đúng A - sai vì: Dao động tắt dần có biên độ giảm dần theo thời gian => Cơ năng của dao động tắt dần giảm dần theo thời gian Động năng cực đại và thế năng cực đại cũng giảm dần
Câu 5 :
Một vật dao động cưỡng bức dưới tác dụng của một ngoại lực biến thiên điều hòa với tần số $f$. Chu kì dao động của vật là:
Đáp án : D Lời giải chi tiết :
Chu kì dao động của vật chính bằng chu kì dao động của ngoại lực và bằng \(T = \frac{1}{f}\)
Câu 6 :
Khi nói về một hệ dao động cưỡng bức ở giai đoạn ổn định, phát biểu nào dưới đây là sai?
Đáp án : B Lời giải chi tiết :
Ta có: A, C, D - đúng B - sai vì: Chỉ khi xảy ra hiện tượng cộng hưởng thì tần số của hệ dao động cưỡng bức mới bằng tần số dao động riêng của hệ
Câu 7 :
Khi nói về dao động cưỡng bức, phát biểu nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
A - sai vì dao động của con lắc đồng hồ là dao động duy trì B - sai vì biên độ của lực cưỡng bức F0 = Aω C - đúng D - sai vì dao động cưỡng bức có tần số bằng tần số của lực cưỡng bức
Câu 8 :
Khi nói về một hệ dao động cưỡng bức ở giai đoạn ổn định, phát biểu nào dưới đây là sai?
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Tần số của hệ dao động cưỡng bức bằng tần số dao động riêng của hệ khi xảy ra cộng hưởng
Câu 9 :
Con lắc lò xo gồm vật nặng m = 100g và lò xo nhẹ có độ cứng \(k = 100N/m\). Tác dụng một ngoại lực cưỡng bức biến thiên điều hòa biên độ \(F_0\) và tần số \(f_1 = 6Hz\) thì biên độ dao động là \(A_1\). Nếu giữ nguyên biên độ \(F_0\) mà tăng tần số ngoại lực đến \(f_2=5,5Hz\) thì biên độ dao động ổn định là \(A_2\). Kết luận đúng là:
Đáp án : D Phương pháp giải :
+ Áp dụng biểu thức tính tần số dao động riêng: \(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} \) + Sử dụng đồ thị A-f Lời giải chi tiết :
Ta có: + Tần số dao động riêng của con lắc: \(f = \dfrac{1}{{2\pi }}\sqrt {\dfrac{k}{m}} = \dfrac{1}{{2\pi }}\sqrt {\dfrac{{100}}{{0,1}}} = 5H{\rm{z}}\) + f0 < f2 < f1 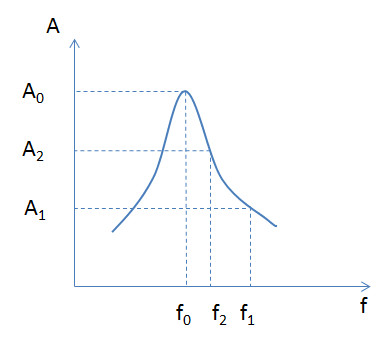 Từ đồ thị ta suy ra: A2 > A1
Câu 10 :
Chọn phát biểu đúng: Dao động duy trì của một hệ là dao động tắt dần mà người ta đã:
Đáp án : C Lời giải chi tiết :
Dao động duy trì là dao động được duy trì bằng cách giữ cho biên độ không đổi mà không làm thay đổi chu kì dao động riêng.
Câu 11 :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động:
Đáp án : A Lời giải chi tiết :
Khi xảy ra hiện tượng cộng hưởng cơ thì vật tiếp tục dao động với tần số bằng tần số dao động riêng của vật
Câu 12 :
Dao động tự do là hệ dao động xảy ra dưới tác dụng của:
Đáp án : C Lời giải chi tiết :
Dao động tự do là hệ dao động xảy ra dưới tác dụng của nội lực kéo về và tần số dao động của hệ chỉ phụ thuộc vào đặc tính bên trong của hệ.
Câu 13 :
Tần số của hệ dao động tự do:
Đáp án : A Lời giải chi tiết :
Tần số của hệ dao động tự do chỉ phụ thuộc vào đặc tính của hệ dao động và không phụ thuộc vào các yếu tố bên ngoài
Câu 14 :
Phát biểu nào sau đây là sai khi nói về dao động cơ học
Đáp án : A Lời giải chi tiết :
A - sai vì: Biên độ dao động cưỡng bức của hệ cơ học khi xảy ra hiện tượng cộng hưởng có phụ thuộc vào lực cản của môi trường 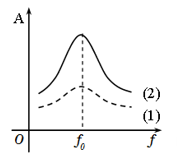
Câu 15 :
Khi xảy ra hiện tượng cộng hưởng thì:
Đáp án : D Lời giải chi tiết :
Ta có, khi xảy ra hiện tượng cộng hưởng: + Vật dao động với tần số bằng tần số dao động riêng + Biên độ dao động của vật đạt giá trị cực đại => năng lượng dao động của vật đạt giá trị cực đại
Câu 16 :
Một người xách một xô nước đi trên đường, mỗi bước dài 45cm. Chu kì dao động riêng của nước trong xô là 0,3s. Để nước trong xô bị dao động mạnh nhất người đó phải đi với tốc độ
Đáp án : D Phương pháp giải :
+ Vận dụng lí thuyết cộng hưởng + Áp dụng công thức \(v = \frac{S}{t}\) Lời giải chi tiết :
Để nước trong xô bị dao động mạnh nhất thì phải xảy ra cộng hưởng cơ => T = T0 = 0,3s Tốc độ khi đó: \(v = \frac{S}{t} = \frac{{0,45}}{{0,3}} = 1,5m/s = 5,4km/h\)
Câu 17 :
Một tấm ván bắc qua một con mương có tần số dao động riêng là 0,5Hz. Một người đi qua tấm ván với bao nhiêu bước trong 12 giây thì tấm ván bị rung lên mạnh nhất?
Đáp án : B Lời giải chi tiết :
Để tấm ván bị rung lên mạnh nhất thì số bước chân của người trên 1s bằng số dao động của tấm ván trên 1s ( cộng hưởng cơ) Ta có, tần số dao động của tấm ván chính là số dao động của tấm ván trên 1s) là 0,5Hz => Số bước chân của người trên 1s là 0,5 bước => Trong 12s người đi qua tấm ván với 12.0,5 = 6 bước thì tấm ván rung lên mạnh nhất
Câu 18 :
Một vật có khối lượng 100g gắn với một lò xo có độ cứng 100N/m. Vật chỉ dao động được trên trục Ox nằm ngang trùng với trục của lò xo. Ban đầu, kéo vật ra khỏi vị trí cân bằng 8cm, rồi truyền cho vật vận tốc 60cm/s hướng theo phương Ox. Trong quá trình dao động vật luôn chịu tác dụng một lực cản không đổi 0,02N. Tổng chiều dài quãng đường mà vật đi được từ lúc bắt đầu dao động cho tới lúc dừng lại:
Đáp án : C Phương pháp giải :
Áp dụng biểu thức W = Fms.s Lời giải chi tiết :
Ta có, toàn bộ năng lượng ban đầu của vật chuyển thành công của lực masát (lực cản) \({\rm{W}} = \frac{1}{2}k{\rm{x}}_0^2 + \frac{1}{2}m{v^2} = {F_{m{\rm{s}}}}s \to s = \frac{{\frac{1}{2}k{\rm{x}}_0^2 + \frac{1}{2}m{v^2}}}{{{F_{m{\rm{s}}}}}} = \frac{{\frac{1}{2}{\rm{100}}{\rm{.(0,08}}{{\rm{)}}^2} + \frac{1}{2}0,1.0,{6^2}}}{{0,02}} = 16,9m\)
Câu 19 :
Một con lắc lò xo có độ cứng 62,5 N/m, vật nặng có khối lượng m=100g dao động trên mặt phẳng nằm ngang. Hệ số masát giữa vật và mặt phẳng ngang là μ=0,1; lấy g=10m/s2. Kéo vật khỏi vị trí cân bằng một đoạn A rồi thả nhẹ. Quãng đường mà vật đã đi cho đến khi dừng hẳn là 2,4m. Giá trị của A là:
Đáp án : C Phương pháp giải :
Áp dụng biểu thức W = Fms.s Lời giải chi tiết :
\({\rm{W}} = \frac{1}{2}kA_0^2 = {F_{m{\rm{s}}}}s = \mu mg.{\rm{s}} \to A = \sqrt {\frac{{2\mu mg.{\rm{s}}}}{k}} = \sqrt {\frac{{2.0,1.0,1.10.2,4}}{{62,5}}} = 0,088m = 8,8cm\)
Câu 20 :
Một con lắc lò xo đang dao động tắt dần, sau ba chu kì đầu tiên biên độ của nó giảm đi 10%. Phần trăm cơ năng còn lại sau khoảng thời gian đó là:
Đáp án : B Phương pháp giải :
Áp dụng biểu thức tính cơ năng: \({\rm{W}} = \frac{1}{2}k{A^2}\) Lời giải chi tiết :
Ta có: \(\frac{{A - {A_3}}}{A} = 10\% = 0,1 \to \frac{{{A_3}}}{A} = 0,9\) Mặt khác, ta có: \({\rm{W}} = \frac{1}{2}k{A^2}\) \( \to \frac{{{{\rm{W}}_3}}}{{\rm{W}}} = \frac{{A_3^2}}{{{A^2}}} = 0,{9^2} = 0,81 = 81\% \) => Phần trăm cơ năng còn lại sau khoảng thời gian đó là 81%
Câu 21 :
Một con lắc dao động tắt dần trong môi trường với lực masát rất nhỏ. Cứ sau mỗi chu kì, phần năng lượng của con lăc bị mất đi 8%. Trong một dao động toàn phần biên độ giảm đi bao nhiêu phần trăm?
Đáp án : B Phương pháp giải :
Phương pháp: Áp dụng biểu thức: \(\frac{{\Delta W}}{{\rm{W}}} = \frac{{2\Delta A}}{A}\) (Xem mục 1 phần II) Lời giải chi tiết :
Ta có: \(\frac{{\Delta W}}{{\rm{W}}} = \frac{{2\Delta A}}{A} = 8\% \to \frac{{\Delta A}}{A} = 4\% \) Vậy trong một dao động toàn phần biên độ giảm đi 4%
Câu 22 :
Con lắc lò xo dao động theo phương ngang, lò xo nhẹ có độ cứng 100N/m, vật nhỏ dao động có khối lượng 100g, hệ số ma sát giữa vật và mặt phẳng ngang là 0,01. Tính độ giảm biên độ mỗi lần vật qua vị trí cân bằng.
Đáp án : D Phương pháp giải :
Áp dụng biểu thức tính độ giảm biên độ sau mỗi chu kì: \(\Delta A = \frac{{4\mu mg}}{k} = \frac{{4\mu g}}{{{\omega ^2}}}\) Lời giải chi tiết :
Ta có, độ giảm biên độ sau mỗi chu kì là: \(\Delta A = \frac{{4\mu mg}}{k}\) => Độ giảm biên độ mỗi lần vật qua VTCB là: \(\frac{{\Delta A}}{2} = \frac{{\frac{{4\mu mg}}{k}}}{2} = \frac{{2\mu mg}}{k} = \frac{{2.0,01.0,1.10}}{{100}} = {2.10^{ - 4}}m = 0,2mm\)
Câu 23 :
Một con lắc lò xo đang dao động tắt dần, cơ năng ban đầu của nó là 5J. Sau ba chu kì kể từ lúc bắt đầu dao động thì biên độ của nó giảm đi 18%. Phần cơ năng của con lắc chuyển hóa thành nhiệt năng tính trung bình trong mỗi chu kì dao động của nó là:
Đáp án : B Phương pháp giải :
Áp dụng công thức tính năng lượng: \({\rm{W}} = \frac{1}{2}k{A^2}\) Lời giải chi tiết :
+ Sau ba chu kì dao động, biên độ còn lại của con lắc là: \({A_3} = A - 0,18A = 0,82A\) + Phần năng lượng bị mất đi sau ba chu kì: \(\begin{array}{l}\Delta {E_3} = E - {E_3} = \frac{{E - {E_3}}}{E}E = \frac{{\frac{1}{2}k{A^2} - \frac{1}{2}kA_3^2}}{{\frac{1}{2}k{A^2}}}E\\ = \frac{{{A^2} - {{(0,82A)}^2}}}{{{A^2}}}.5 = 1,638J\end{array}\) + Phần cơ năng chuyển hóa thành nhiệt năng trung bình trong mỗi chu kì: \(\Delta E = \frac{{1,638}}{3} = 0,546J\)
Câu 24 :
Một con lắc lò xo, vật nặng có khối lượng 100g, lò xo có độ cứng 100N/m, dao động trên mặt phẳng ngang với biên độ ban đầu 10cm. Lấy gia tốc trọng trường 10m/s2. Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,1. Số dao động thực hiện được kể từ lúc dao động cho đến lúc dừng lại là:
Đáp án : A Phương pháp giải :
+ Áp dụng biểu thức tính độ giảm biên độ sau mỗi chu kì: \(\Delta A = \frac{{4\mu mg}}{k}\) + Áp dụng biểu thức tính số dao động vật thực hiện được cho đến lúc dừng lại: \(N = \frac{A}{{\Delta A}}\) Lời giải chi tiết :
Ta có: + Độ giảm biên độ sau mỗi chu kì: \(\Delta A = \frac{{4\mu mg}}{k}\) + Số dao động vật thực hiện được cho đến lúc dừng lại: \(N = \frac{A}{{\Delta A}} = \frac{{Ak}}{{4\mu mg}} = \frac{{0,1.100}}{{4.0,1.0,1.10}} = 25\)
Câu 25 :
Một con lắc lò xo, vật nặng có khối lượng 100g, lò xo có độ cứng 100N/m, dao động trên mặt phẳng ngang với biên độ ban đầu 10cm. Lấy gia tốc trọng trường 10m/s2. Biết hệ số ma sát giữa vật và mặt phẳng ngang là 0,1. Tìm thời gian từ lúc dao động cho đến lúc dừng lại.
Đáp án : A Phương pháp giải :
Áp dụng biểu thức tính thời gian từ lúc vật dao động đến khi dừng lại: \(\Delta t = N.T = \frac{{AkT}}{{4\mu mg}} = \frac{{\pi \omega A}}{{2\mu g}}\) Lời giải chi tiết :
Thời gian từ lúc vật dao động đến khi dừng lại là: \(\Delta t = N.T = \frac{{AkT}}{{4\mu mg}} = \frac{{Ak2\pi \sqrt {\frac{m}{k}} }}{{4\mu mg}} = \frac{{A.2\pi \sqrt k }}{{4\mu g\sqrt m }} = \frac{{0,1.2\pi \sqrt {100} }}{{4.0,1.10\sqrt {0,1} }} = 5{\rm{s}}\)
Câu 26 :
Một vật nhỏ nối với một lò xo nhẹ, hệ dao động trên mặt phẳng ngang. Từ vị trí cân bằng truyền cho vật vận tốc ban đầu 2m/s theo phương ngang thì vật dao động tắt dần. Tốc độ trung bình trong suốt quá trình vật dao động là:
Đáp án : C Phương pháp giải :
+ Áp dụng công thức tính quãng đường đi được từ lúc dao động đến khi dừng lại: \(S = \frac{{k{A^2}}}{{2\mu mg}} = \frac{{{\omega ^2}{A^2}}}{{2\mu g}}\) + Áp dụng biểu thức tính thời gian từ lúc vật dao động đến khi dừng lại: \(\Delta t = N.T = \frac{{AkT}}{{4\mu mg}} = \frac{{\pi \omega A}}{{2\mu g}}\) + Áp dụng biểu thức xác định tốc độ trung bình của vật: \({v_{tb}} = \frac{S}{{\Delta t}}\) Lời giải chi tiết :
Ta có: + Quãng đường đi được từ lúc dao động đến khi dừng lại: \(S = \frac{{k{A^2}}}{{2\mu mg}} = \frac{{{\omega ^2}{A^2}}}{{2\mu g}}\) + Thời gian từ lúc vật dao động đến khi dừng lại: \(\Delta t = N.T = \frac{{AkT}}{{4\mu mg}} = \frac{{\pi \omega A}}{{2\mu g}}\) Tốc độ trung bình của vật trong suốt quá trình vật dao động: \({v_{tb}} = \frac{S}{{\Delta t}} = \frac{{\frac{{{\omega ^2}{A^2}}}{{2\mu g}}}}{{\frac{{\pi \omega A}}{{2\mu g}}}} = \frac{{\omega A}}{\pi } = \frac{2}{\pi } = 0,6366m/s = 63,66cm/s\)
Câu 27 :
Thực hiện thí nghiệm về dao động cưỡng bức như hình bên. Năm con lắc đơn: (1), (2), (3), (4) và M (con lắc điều khiển) được treo trên một sợi dây. Ban đầu hệ đang đứng yên ở vị trí cân bằng. Kích thích M dao động nhỏ trong mặt phẳng vuông góc với mặt phẳng hình vẽ thì các con lắc còn lại dao động theo. Không kể M, con lắc dao động mạnh nhất là 
Đáp án : B Phương pháp giải :
Sử dụng lý thuyết về cộng hưởng dao động Lời giải chi tiết :
Khi M dao động thì tác dụng 1 lực cưỡng bức lên dây treo. Lực này lại tác dụng lên các con lắc còn lại làm cho các con lắc dao động. Nói cách khác con lắc 1, 2, 3, 4 chịu tác dụng của 1 ngoại lực biến thiên tuần hoàn nên nó dao động cưỡng bức. Lực này biến thiên với tần số đúng bằng tần số dao động của M Trong dao động cưỡng bức, khi tần số của ngoại lực càng gần với tần số dao động riêng thì con lắc sẽ dao động với biên độ càng lớn. Vậy con lắc nào có chiều dài gần với chiều dài của M nhất thì sẽ dao động mạnh nhất.
Câu 28 :
Giảm xóc của ô tô là áp dụng của
Đáp án : B Lời giải chi tiết :
Giảm xóc của ô tô là áp dụng của dao động tắt dần
Câu 29 :
Một con lắc lò xo dao động tắt dần trên mặt phẳng nằm ngang. Cứ sau mỗi chu kì biên độ giảm 2%. Gốc thế năng tại vị trí của vật mà lò xo không biến dạng. Phần trăm cơ năng của con lắc bị mất đi trong hai dao động toàn phần liên tiếp có giá trị gần nhất với giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Công thức tính cơ năng: \({\rm{W}} = \dfrac{1}{2}k{A^2}\) Dựa vào dữ kiện “Cứ sau mỗi chu kì biên độ giảm 2%” để tính biên độ dao động của vật sau hai dao động toàn phần liên tiếp. Phần trăm cơ năng mất đi: \(\Delta {\rm{W}} = \dfrac{{{\rm{W}} - {{\rm{W}}_2}}}{{\rm{W}}}.100\% = \dfrac{{{A^2} - A_2^2}}{{{A^2}}}.100\% \) Lời giải chi tiết :
Ban đầu biên độ dao động của vật là A Sau 1 dao động toàn phần biên độ dao động của vật là: \({A_1} = A - 0,02A = 0,98A\) Sau 2 dao động toàn phần biên độ dao động của vật là: \({A_2} = {A_1} - 0,02{A_1} = 0,98A - 0,02.0,98A = 0,9604A\) Phần trăm cơ năng mất đi sau 2 dao động toàn phần liên tiếp là: \(\begin{array}{l}\Delta {\rm{W}} = \dfrac{{{\rm{W}} - {{\rm{W}}_2}}}{{\rm{W}}}.100\% = \dfrac{{{A^2} - A_2^2}}{{{A^2}}}.100\% \\ \Rightarrow \Delta {\rm{W}} = \dfrac{{{A^2} - 0,{{9604}^2}.{A^2}}}{{{A^2}}}.100\% = 7,8\% \end{array}\)
Câu 30 :
Con lắc đơn dao động trong môi trường không khí. Kéo con lắc lệch phương thẳng đứng một góc 0,1 rad rồi thả nhẹ. Biết lực cản của không khí tác dụng lên con lắc là không đổi và bằng 0,001 lần trọng lượng của vật. Coi biên độ giảm đều trong từng chu kỳ. Số lần con lắc qua vị trí cân bằng đến lúc dừng lại là:
Đáp án : A Phương pháp giải :
Cơ năng của con lắc đơn: \({\rm{W}} = \dfrac{1}{2}mgl{\alpha _0}^2\) Công của lực cản: \(A = {F_c}.l\alpha \) Lời giải chi tiết :
Ban đầu con lắc có biên độ góc là \({\alpha _0}\), khi đi qua VTCB lần đầu, sang bên khi nó có biên độ \(\alpha \). Độ giảm năng lượng bằng công của lực ma sát: \(\begin{array}{l}\Delta {\rm{W}} = A \Rightarrow \dfrac{1}{2}mgl\left( {{\alpha _0}^2 - {\alpha ^2}} \right) = 0,001mg.l\left( {\alpha + {\alpha _0}} \right)\\ \Rightarrow \Delta \alpha = {\alpha _0} - \alpha = \dfrac{{0,001mgl}}{{\dfrac{1}{2}mgl}} = 0,002\,\,\left( {rad} \right)\end{array}\) Số lần con lắc đi qua vị trí cân bằng là: \(n = \dfrac{{{\alpha _0}}}{{\Delta \alpha }} = \dfrac{{0,1}}{{0,002}} = 50\) (lần) Chọn A.
Câu 31 :
Một vật chịu tác dụng của ngoại lực có biểu thức Fn = F0cos(10πt + π/2) thì xảy ra hiện tượng cộng hưởng. Tần số dao động riêng của vật là
Đáp án : C Phương pháp giải :
Hiện tượng cộng hưởng xảy ra khi tần số góc của ngoại lực: ω = Ω Tần số: \(f = \dfrac{\omega }{{2\pi }}\) Lời giải chi tiết :
Hiện tượng cộng hưởng xảy ra khi: \(\omega = {\omega _0} = 10\pi \Rightarrow f = \dfrac{{10\pi }}{{2\pi }} = 5\left( {Hz} \right)\)
Câu 32 :
Một con lắc lò xo gồm vật nhỏ nhỏ có khối lượng 100 gam và lò xo nhẹ có độ cứng 40 N/m. Cho con lắc dao động lần lượt dưới tác dụng của ngoại lực: F1 = 2cos5t (N); F2 = 2cos20t (N); F3 = 2cos30t (N) và F4 = 2cos25t (N), trong đó t tính bằng s. Hiện tượng cộng hưởng xảy ra khi con lắc chịu tác dụng của ngoại lực là
Đáp án : B Phương pháp giải :
Tần số góc của con lắc lò xo: \(\omega = \sqrt {\frac{k}{m}} \) Hiện tượng cộng hưởng xảy ra khi tần số của ngoại lực: Ω = ω Lời giải chi tiết :
Tần số góc của con lắc là: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{40}}{{0,1}}} = 20\,\,\left( {rad/s} \right)\) Hiện tượng cộng hưởng xảy ra khi ngoại lực có tần số: Ω = ω = 20 rad/s → con lắc chịu tác dụng của ngoại lực F2
Câu 33 :
Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động
Đáp án : D Phương pháp giải :
Sử dụng lí thuyết về các loại dao động. Lời giải chi tiết :
Dao động được tạo ra bằng cách cung cấp cho hệ một năng lượng đúng bằng năng lượng nó đã mất sau mỗi chu kì gọi là dao động duy trì.
Câu 34 :
Đề thi THPT QG - 2020 Một con lắc đơn có chiều dài 70 cm đang dao động cưỡng bức với biên độ góc nhỏ, tại nơi có g=10m/s2. Khi có cộng hưởng, con lắc dao động điều hòa với chu kì là
Đáp án : A Phương pháp giải :
+ Vận dụng lí thuyết cộng hưởng dao động + Sử dụng biểu thức tính chu kì dao động con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \) Lời giải chi tiết :
Khi xảy ra cộng hưởng, chu kì dao động của lực cưỡng bức bằng chu kì dao động riêng của hệ Ta có: \(T = 2\pi \sqrt {\frac{l}{g}} = 2\pi \sqrt {\frac{{0,7}}{{10}}} = 1,66s\)
Câu 35 :
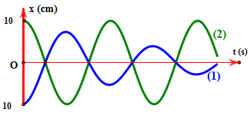
Hai chất điểm dao động có li độ phụ thuộc theo thời gian được biểu diễn tương ứng bởi hai đồ thị (1) và (2) như hình vẽ, Nhận xét nào dưới đây đúng khi nói về dao động của hai chất điểm?
Đáp án : B Phương pháp giải :
Sử dụng lí thuyết về các loại dao động. Lời giải chi tiết :
Từ đồ thị, ta thấy hai chất diểm dao động với cùng biên độ và chu kì. Chất điểm (1) dao động tắt dần, và chất điểm (2) dao động điều hòa. \( \Rightarrow \) B đúng.
Câu 36 :
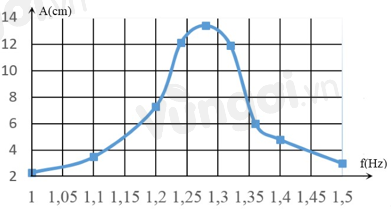
Khảo sát thực nghiệm một con lắc lò xo gồm vật nhỏ có khối lượng \(216g\) và lò xo có độ cứng \(k\), dao động dưới tác dụng của ngoại lực \(\text{F = }{{\text{F}}_{\text{0}}}\text{cos2 }\!\!\pi\!\!\text{ ft}\), với \({{F}_{0}}\) không đổi và \(f\) thay đổi được. Kết quả khảo sát ta được đường biểu diễn biên độ \(A\) của con lắc theo tần số \(f\) có đồ thị như hình vẽ. Giá trị của \(k\) gần nhất với giá trị nào sau đây?
Đáp án : A Phương pháp giải :
Tần số dao động của con lắc: \(f=\dfrac{1}{2\pi }\sqrt{\dfrac{k}{m}}\) Hiện tượng cộng hưởng cơ: Biên độ của dao động cưỡng bức đạt cực đại khi tần số của ngoại lực bằng tần số riêng. Lời giải chi tiết :
Từ đồ thị ta thấy biên độ dao động của con lắc lớn nhất khi tần số của ngoại lực bằng 1,275 Hz. Khi đó xảy ra hiện tượng cộng hưởng, tần số của ngoại lực bằng tần số đao dộng riêng của con lắc. Vậy tần số riêng của con lắc là: \(\begin{array}{l}
Câu 37 :
Một cây cầu bắc ngang qua sông Phô-tan-ka ở thành phố Xanh Pê-téc-bua (Nga) được thiết kế xây dựng đủ vững chắc, có thể cho cùng lúc 300 người đi qua mà cầu không sập. Năm 1906 có một trung đội bộ binh gồm 36 người đi đều bước qua cây cầu làm cho cây cầu gãy. Sự cố gãy cầu là do
Đáp án : B Phương pháp giải :
Sử dụng lý thuyết dao động cưỡng bức và cộng hưởng Lời giải chi tiết :
Sự cố gãy cầu là do xảy ra hiện tượng cộng hưởng cơ ở cầu
|



















Danh sách bình luận